| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Выбор решения при однократном наблюдении
Обсуждение проблемы выбора решения на основе одного наблюдения начнем с определения вероятностей ложной тревоги и пропуска сигнала. Согласно предположению, введенному в конце предыдущего параграфа, для вероятности пропуска сигнала можно записать (см. рис. 5.2)
 . (5.1)
. (5.1)
Аналогично для вероятности ложной тревоги получаем
 . (5.2)
. (5.2)
Из этих формул следует,
что, например, вероятность пропуска можно получить сколь угодно малой, если
только не обращать внимания (на вероятность ложной тревоги. В практических
приложениях обычно вероятность ложной тревоги ![]() выбирается равной некоторой допустимой
величине, а правило решения (т. е. порог
выбирается равной некоторой допустимой
величине, а правило решения (т. е. порог ![]() ) выбирается так, чтобы обеспечить
минимально возможное значение вероятности пропуска
) выбирается так, чтобы обеспечить
минимально возможное значение вероятности пропуска ![]() . Этот критерий, известный как
критерий Неймана-Пирсона, в рассматриваемом здесь случае оказывается
тривиальным. Действительно, для обеспечения заданного значения вероятности
ложной тревоги здесь необходимо соответствующим образом выбрать и
зафиксировать значение порога, что приведет к вполне определенному значению
вероятности пропуска сигнала.
. Этот критерий, известный как
критерий Неймана-Пирсона, в рассматриваемом здесь случае оказывается
тривиальным. Действительно, для обеспечения заданного значения вероятности
ложной тревоги здесь необходимо соответствующим образом выбрать и
зафиксировать значение порога, что приведет к вполне определенному значению
вероятности пропуска сигнала.
В более реальных случаях, когда имеется несколько (наблюдений, оказывается возможным, используя метод множителей Лагранжа, наложить ограничение на вероятность ложной тревоги, не фиксируя одновременно значение вероятности пропуска сигнала. Следовательно, в этом случае можно найти минимум выражения
![]() , (5.3)
, (5.3)
в котором ![]() — неопределенный
множитель Лагранжа, а
— неопределенный
множитель Лагранжа, а ![]() — требуемое значение вероятности ложной
тревоги. Используя теперь равенства (5.1) и (5.2) и дифференцируя (5.3) по
— требуемое значение вероятности ложной
тревоги. Используя теперь равенства (5.1) и (5.2) и дифференцируя (5.3) по ![]() , запишем
, запишем
![]() .
.
Отсюда получаем правило выбора решения
 , (5.4)
, (5.4)
основывающееся на отношении правдоподобия, при
наблюдении ![]() .
Согласно этому правилу гипотеза
.
Согласно этому правилу гипотеза ![]() принимается в том случае, если это
отношение больше
принимается в том случае, если это
отношение больше ![]() ,
а гипотеза
,
а гипотеза ![]() принимается,
если отношение правдоподобия меньше
принимается,
если отношение правдоподобия меньше ![]() . Параметр
. Параметр ![]() (множитель Лагранжа) выбирается из
условия
(множитель Лагранжа) выбирается из
условия ![]() .
.
Если ложное обнаружение и пропуск сигнала имеют одинаковые последствия, то можно «минимизировать сумму вероятностей пропуска сигнала и ложной тревоги
 (5.5)
(5.5)
путем выбора порога ![]() Дифференцируя правую часть последнего
равенства по
Дифференцируя правую часть последнего
равенства по ![]() и
приравнивая производную нулю, получим
и
приравнивая производную нулю, получим
![]() .
.
Таким образом, значение
порога ![]() совпадает
с тем значением переменной
совпадает
с тем значением переменной ![]() , при котором оказываются равными значения
плотностей вероятности. Если для полученного значения
, при котором оказываются равными значения
плотностей вероятности. Если для полученного значения ![]() оказывается,
что
оказывается,
что ![]() , то
принимается гипотеза
, то
принимается гипотеза ![]() . Правило выбора решения в
рассматриваемом случае также основывается на отношении правдоподобия и
записывается в виде
. Правило выбора решения в
рассматриваемом случае также основывается на отношении правдоподобия и
записывается в виде
 . (5.6)
. (5.6)
Реальные проблемы выбора решения вообще намного сложнее, чем рассматриваемая здесь задача при простом скалярном наблюдении. Часто, например, представляется неестественным предположение, что ложная тревога и пропуск сигнала приводят к одинаковым последствиям. В общем случае с этими ошибками могут быть связаны различные потери, кроме того, потери могут быть приписаны правильным решениям. При рассмотрении задач подобного типа используется критерий байесовского риска, а соответствующие правила называются байесовскими правилами выбора решения.
При проверке гипотезы против одной единственной альтернативы возможны четыре ситуации и следующие связанные с ними потери:
![]() - потери при принятии гипотезы
- потери при принятии гипотезы
![]() , когда на
самом деле справедлива гипотеза
, когда на
самом деле справедлива гипотеза ![]() ;
;
![]() - потери при принятии гипотезы
- потери при принятии гипотезы
![]() , когда на
самом деле справедлива гипотеза
, когда на
самом деле справедлива гипотеза ![]() ;
;
![]() - потери при принятии гипотезы
- потери при принятии гипотезы
![]() , когда на
самом деле справедлива гипотеза
, когда на
самом деле справедлива гипотеза ![]() ;
;
![]() - потери при принятии гипотезы
- потери при принятии гипотезы
![]() , когда на
самом деле справедлива гипотеза
, когда на
самом деле справедлива гипотеза ![]() .
.
![]() и
и ![]() характеризуют потери при
принятии правильных решений, в то время как
характеризуют потери при
принятии правильных решений, в то время как ![]() и
и ![]() - потери при ошибочных решениях.
- потери при ошибочных решениях.
Определим байесовский риск
![]() как среднее
значение потерь в указанных выше четырех ситуациях. Тогда можно записать
как среднее
значение потерь в указанных выше четырех ситуациях. Тогда можно записать ![]() (принять
(принять ![]() ,
, ![]() справедлива) +
справедлива) + ![]() (принять
(принять ![]() ,
, ![]() справедлива) +
справедлива) + ![]() (принять
(принять ![]() ,
, ![]() справедлива) +
справедлива) + ![]() (принять
(принять ![]() ,
, ![]() справедлива).
справедлива).
Воспользовавшись
правилом умножения вероятностей ![]() ,
выражение для риска можно переписать следующим образом:
,
выражение для риска можно переписать следующим образом:

Если теперь правило
выбора решения представляет собой простое сравнение результата наблюдения с
порогом, т. е. согласно этому правилу принимается гипотеза ![]() если полученное значение
если полученное значение ![]() наблюдаемой величины больше порогового значения
наблюдаемой величины больше порогового значения ![]() и
принимается гипотеза
и
принимается гипотеза ![]() , если
, если ![]() , то риск
, то риск ![]() можно записать «в виде следующего
выражения:
можно записать «в виде следующего
выражения:
 (5.8)
(5.8)
Значение порога ![]() теперь необходимо
выбрать так, чтобы минимизировать значение байесовского риска (5.8) Естественно
предположить, что потери при неправильных решениях будут больше, чем потери при
правильных решениях (часто потери при правильных решениях принимают равными
нулю), т. е.
теперь необходимо
выбрать так, чтобы минимизировать значение байесовского риска (5.8) Естественно
предположить, что потери при неправильных решениях будут больше, чем потери при
правильных решениях (часто потери при правильных решениях принимают равными
нулю), т. е. ![]() и
и
![]() . Будем
считать также, что потери при любых решениях неотрицательны.
. Будем
считать также, что потери при любых решениях неотрицательны.
Так как
 , (5.9)
, (5.9)
то вместо (5.8) можно записать
 . (5.10)
. (5.10)
От порога ![]() в последнем выражении зависит только
значение интеграла. Дифференцируя риск
в последнем выражении зависит только
значение интеграла. Дифференцируя риск ![]() по
по ![]() и приравнивая производную нулю, получим
равенство
и приравнивая производную нулю, получим
равенство
![]() , (5.11)
, (5.11)
являющееся необходимым условием, которому должен
удовлетворять порог ![]() . Эквивалентной является следующая форма
записи этого условия:
. Эквивалентной является следующая форма
записи этого условия:
 .
(5.12)
.
(5.12)
В действительности значение наблюдения ![]() может оказаться
меньшим или равным порогу
может оказаться
меньшим или равным порогу ![]() . Из ф-лы (5.10) рис.
5.2 следует, что если
. Из ф-лы (5.10) рис.
5.2 следует, что если ![]() окажется меньше, чем
окажется меньше, чем ![]() , то условная плотность
вероятности
, то условная плотность
вероятности ![]() при
при
![]() возрастет, в
то время как условная плотность вероятности
возрастет, в
то время как условная плотность вероятности ![]() при
при ![]() уменьшится.
уменьшится.
То есть, в этом случае отношение ![]() уменьшится. Следовательно,
правило выбора решения можно определить следующим образом:
уменьшится. Следовательно,
правило выбора решения можно определить следующим образом:
 . (5.13)
. (5.13)
Отношение двух рассматриваемых плотностей вероятностей называется отношением правдоподобия
 . (5.14)
. (5.14)
Порог данного правила выбора решения имеет вид
![]() .
(5.15)
.
(5.15)
Используя эти обозначения, правило выбора решения, наилучшее в смысле критерия среднего риска, можно записать в виде
![]() . (5.16)
. (5.16)
Часто полезно преобразовать соотношение (5.16), взяв, например, натуральный логарифм от его обеих частей. В этом случае получаем
![]() . (5.17)
. (5.17)
Такое преобразование особенно удобно в том случае,
когда обе рассматриваемые плотности вероятности являются нормальными. В последующем
анализе предполагается, что имеется вся информация, необходимая для вычисления
значения порога ![]() данного
правила. В действительности значения потерь и априорных вероятностей обычно
неизвестны и должны быть определены из каких-либо дополнительных соображений
или на основе результатов дополнительной обработки реальных наблюдений, что приводит
к адаптивным правилам выбора решения.
данного
правила. В действительности значения потерь и априорных вероятностей обычно
неизвестны и должны быть определены из каких-либо дополнительных соображений
или на основе результатов дополнительной обработки реальных наблюдений, что приводит
к адаптивным правилам выбора решения.
Иногда потери известны, а неизвестными остаются только
априорные вероятности ![]() и
и ![]() . В этом случае можно использовать
минимаксное правило выбора решения, являющееся байесовским для наихудших
значений априорных вероятностей. Это означает, что минимаксный риск
. В этом случае можно использовать
минимаксное правило выбора решения, являющееся байесовским для наихудших
значений априорных вероятностей. Это означает, что минимаксный риск
![]() (5.18)
(5.18)
равен минимально возможному значению среднего риска
при таком значении ![]() ,
которое максимизирует этот риск. Минимаксный критерий имеет некоторые
преимущества по сравнению с критерием среднего риска. Однако следует иметь в
виду, что он может привести к чрезмерно осторожным правилам выбора решения.
,
которое максимизирует этот риск. Минимаксный критерий имеет некоторые
преимущества по сравнению с критерием среднего риска. Однако следует иметь в
виду, что он может привести к чрезмерно осторожным правилам выбора решения.
Воспользовавшись формулами для вероятностей пропуска сигнала и ложной тревоги, выражение (5.10) для байесовского риска можно переписать следующим образом:
![]() .
.
Но так как ![]() , то
, то
![]() . (5.19)
. (5.19)
Если желательно получить минимаксное правило, то порог
нужно выбрать так, чтобы байесовский риок не зависел от значения ![]() . Следовательно,
коэффициент при
. Следовательно,
коэффициент при ![]() в
ф-ле (5.19) должен быть равен нулю и для минимаксного правила
получаем
в
ф-ле (5.19) должен быть равен нулю и для минимаксного правила
получаем
![]() .
(5.20)
.
(5.20)
Отсюда для особенно важного случая, когда ![]() , имеем
, имеем
![]() . (5.21)
. (5.21)
Последнее равенство можно рассматривать как соотношение, определяющее минимаксное правило.
Отношение правдоподобия ![]() играет очень важную роль при изучении
вопросов, рассматриваемых в данной книге. Все правила выбора решения,
рассмотренные до сих пор, основываются на отношении правдоподобия.
играет очень важную роль при изучении
вопросов, рассматриваемых в данной книге. Все правила выбора решения,
рассмотренные до сих пор, основываются на отношении правдоподобия.
Байесовское правило выбора решения минимизирует апостериорный риск. Это становится очевидным, если воспользоваться формулой Байеса и записать отношение правдоподобия (5.14) в виде
 .
(5.22)
.
(5.22)
Первый сомножитель правой части этого выражения представляет собой отношение апостериорных вероятностей рассматриваемых гипотез. Отметим здесь, что в данной книге апостериорные распределения постоянно будут служить предметом внимательного изучения.
Пример 5.1. Простейшей задачей, относящейся к рассматриваемой в
данном разделе проблеме построения правила выбора решения, является обнаружение
постоянного сигнала на фоне аддитивного нормального шума, среднее значение
которого равно нулю Здесь гипотезе ![]() соответствует отсутствие сигнала,
согласно гипотезе
соответствует отсутствие сигнала,
согласно гипотезе ![]() сигнал
со значением
сигнал
со значением ![]() присутствует
на всем интервале наблюдения, т е можно записать
присутствует
на всем интервале наблюдения, т е можно записать ![]() , где
, где
![]() .
.
Задача проверки гипотез возникает, например, тогда, когда необходимо проверить, какому из двух возможных значений — 0 или ![]() — равно среднее значение нормальной случайной величины Для вычисления
отношения правдоподобия необходимо знать плотности вероятности, соответствующие
разным гипотезам Для рассматриваемого примера имеем
— равно среднее значение нормальной случайной величины Для вычисления
отношения правдоподобия необходимо знать плотности вероятности, соответствующие
разным гипотезам Для рассматриваемого примера имеем
![]() ;
;
![]() .
.
Логарифм отношения правдоподобия
![]() .
.
Байесовское правило выбора решения имеет вид

или
 .
.
Согласно этому правилу
решение выносится после сравнения полученного значения а наблюдаемой величины
со значением порога ![]() .
Это выражение для правила получено непосредственно из соотношения (5.17).
.
Это выражение для правила получено непосредственно из соотношения (5.17).
Если потери при
правильных решениях принять равными нулю, т.е. положить ![]() , а потери при ошибках обоих
видов — отличными от нуля и равными, то правило проверки рассматриваемых
гипотез записывается в виде
, а потери при ошибках обоих
видов — отличными от нуля и равными, то правило проверки рассматриваемых
гипотез записывается в виде
 .
.
Если ![]() , то порог этого правила меньше, чем
, то порог этого правила меньше, чем ![]() . Поскольку гипотеза
. Поскольку гипотеза ![]() оказывается
справедливой чаще, чем
оказывается
справедливой чаще, чем ![]() . При
. При ![]() значение порога точно равно
значение порога точно равно ![]() , что интуитивно
представляется естественным, поскольку гипотезы
, что интуитивно
представляется естественным, поскольку гипотезы ![]() и
и ![]() априори одинаково правдоподобны
априори одинаково правдоподобны
Вероятности пропуска сигнала и ложной тревоги, определяемые соотношениями (5.1) и (5.2) соответственно, в данном примере легко вычисляются
 ,
,
 .
.
Эти формулы после замены переменных приводятся к виду

Вероятность правильного обнаружения
 .
.
Взаимосвязь между вероятностями правильного
обнаружения ![]() и ложной тревоги
и ложной тревоги ![]() можно охарактеризовать с помощью семейства
кривых, для которого
можно охарактеризовать с помощью семейства
кривых, для которого ![]() является параметром с дискретным множеством
возможных значений, а
является параметром с дискретным множеством
возможных значений, а ![]() — параметром со значениями из интервала
— параметром со значениями из интервала ![]() .
.
При ![]() всегда принимается только
гипотеза
всегда принимается только
гипотеза ![]() . В
этом случае вероятности и ложной тревоги, и правильного обнаружения равны 1 При
. В
этом случае вероятности и ложной тревоги, и правильного обнаружения равны 1 При
![]() всегда
принимается гипотеза
всегда
принимается гипотеза ![]() . Очевидно, что при заданном значении
. Очевидно, что при заданном значении ![]() вероятность
правильного обнаружения
вероятность
правильного обнаружения ![]() монотонно
возрастает с увеличением
монотонно
возрастает с увеличением ![]() . Семейство таких кривых, которые часто
называются рабочими характеристики приемника приведено на рис 5.3
. Семейство таких кривых, которые часто
называются рабочими характеристики приемника приведено на рис 5.3

Рис.5.3 Рабочие
характеристики приемника (пример 5.1). Стрелками указаны направления вдоль
которых значения параметров ![]() и
и ![]() увеличиваются.
увеличиваются.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие к русскому изданию
- Глава 1. Обзор содержания книги
- Глава 2. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 2.1. Введение
- 2.2. Теория вероятностей
- 2.3. Случайные величины
- 2.4. Алгебраические действия над случайными величинами
- 2.5. Средние значения
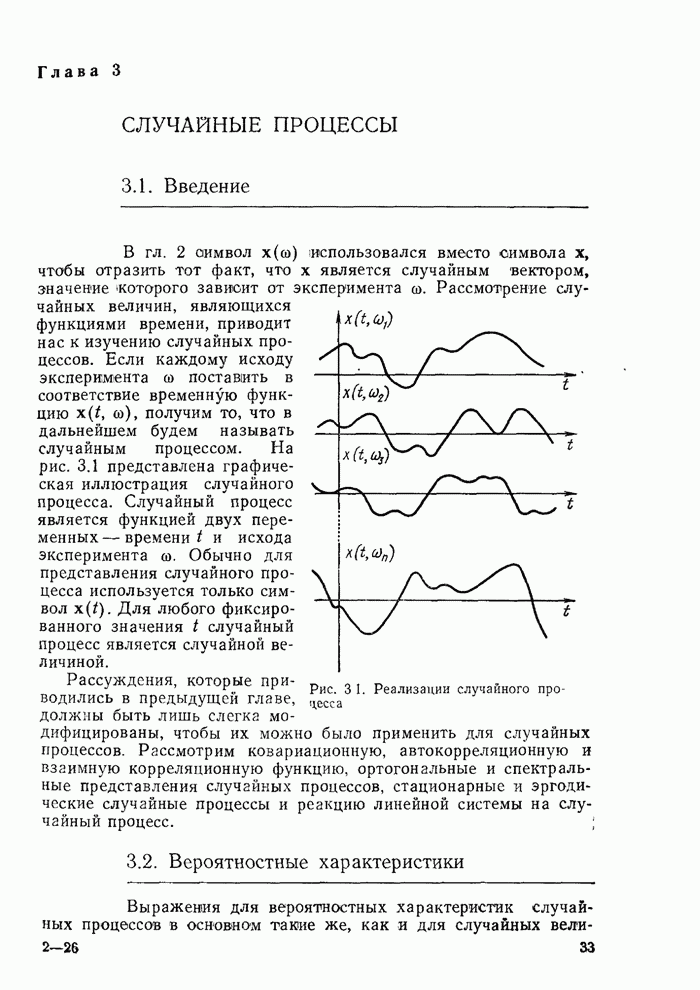
- Глава 3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 3.1. Введение
- 3.2. Вероятностные характеристики
- 3.3. Средние значения
- 3.4. Спектральные и ортогональные представления
- 3.5. Реакция линейных систем
- Глава 4. НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ И СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 4.1. Введение
- 4.2. Нормальные случайные процессы
- 4.3. Марковские случайные процессы
- 4.4. Стохастические дифференциальные уравнения
- 4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы
- Глава 5. ТЕОРИЯ РЕШЕНИЙ
- 5.1. Введение
- 5.2. Выбор решения при однократном наблюдении
- 5.3. Выбор решения при многократных наблюдениях
- 5.4. Проверка сложных гипотез
- 5.5. Проверка многих гипотез
- 5.6. Последовательный анализ
- 5.7. Последовательное обнаружение марковских сигналов в нормальном шуме
- Глава 6. ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
- 6.1. Введение
- 6.2. Байесовские оценки
- 6.3. Оценки максимального правдоподобия
- 6.4. Свойства оценок
- 6.5. Точность оценок и априорная информация
- 6.6. Линейные оценки с минимальной среднеквадратической ошибкой
- 6.7. Оценки наименьших квадратов
- Глава 7. ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
- 7.1. Введение
- 7.2. Оптимальный линейный дискретный фильтр
- 7.3. Оптимальный линейный непрерывный фильтр
- 7.4. Стационарные процессы и фильтр Винера
- 7.5. Асимптотические свойства
- Глава 8. ОБОБЩЕНИЕ АЛГОРИТМА ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.1. Введение
- 8.2. Небелый шум
- 8.3. Сглаживание и предсказание
- 8.4. Анализ ошибок и априорные данные
- 8.5. Расходимость
- Глава 9. НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
- 9.1. Введение
- 9.2 Оценивание при помощи условного среднего
- 9.3. Оценивание по максимуму апостериорной вероятности
- 9.4. Соотношения между нелинейными алгоритмами фильтрации
- 9.5. Нелинейное сглаживание
- Список литературы