4. Свойства и возможности вейвлет-преобразования

Одномерное преобразование Фурье дает также одномерную информацию об относительном вкладе (амплитудах) разных временных масштабов (частот). Результатом вейвлет-преобразования одномерного ряда является двумерный массив амплитуд вейвлет-преобразования — значений коэффициентов Распределение этих значений в пространстве (временной масштаб, временная локализация) дает информацию об эволюции относительного вклада компонент разного масштаба во времени и называется спектром коэффициентов вейвлет-преобразования, (частотно-) масштабно-временным спектром или вейвлет-спектром (time-scale spectrum, или wavelet spectrum в отличие от single spectrum преобразования Фурье).

4.1. Способы представления результатов

Спектр одномерного сигнала представляет собой поверхность в трехмерном пространстве. Способы визуализации этой информации могут быть различными. Вместо изображения поверхностей часто представляют их проекции на плоскость с изолиниями или изоуровнями, позволяющими проследить изменение интенсивности амплитуд вейвлет-преобразования на разных масштабах и во времени, а также картины линий локальных экстремумов этих поверхностей (так называемый "sceleton"), четко выявляющие структуру анализируемого процесса. Термин "скелет" или "скелетон" хорошо отражает характер картин линий локальных экстремумов (см. примеры), и мы будем использовать его для краткости.

В тех случаях, когда необходимо показать очень широкий диапазон масштабов, визуализация результатов в логарифмических координатах, например, предпочтительнее, чем в линейных.

Продемонстрируем сказанное на примере преобразования конкретного сигнала, не касаясь физической интерпретации. На рисунке 3 представлены результаты вейвлет-преобразования временного ряда потока ионов солнечного ветра (данные получены с помощью прибора МОНИТОР [12] на спутнике Прогноз-8; результаты их анализа частично опубликованы в [12]). В вычислениях использовался МНАТ-вейвлет.

На рисунке 3а-в показаны анализируемый ряд, картина значений коэффициентов вейвлет-преобразования и скелетон в проекциях на плоскость (временной масштаб, время); по оси абсцисс отложено время (или параметр сдвига), по оси ординат — временной масштаб.

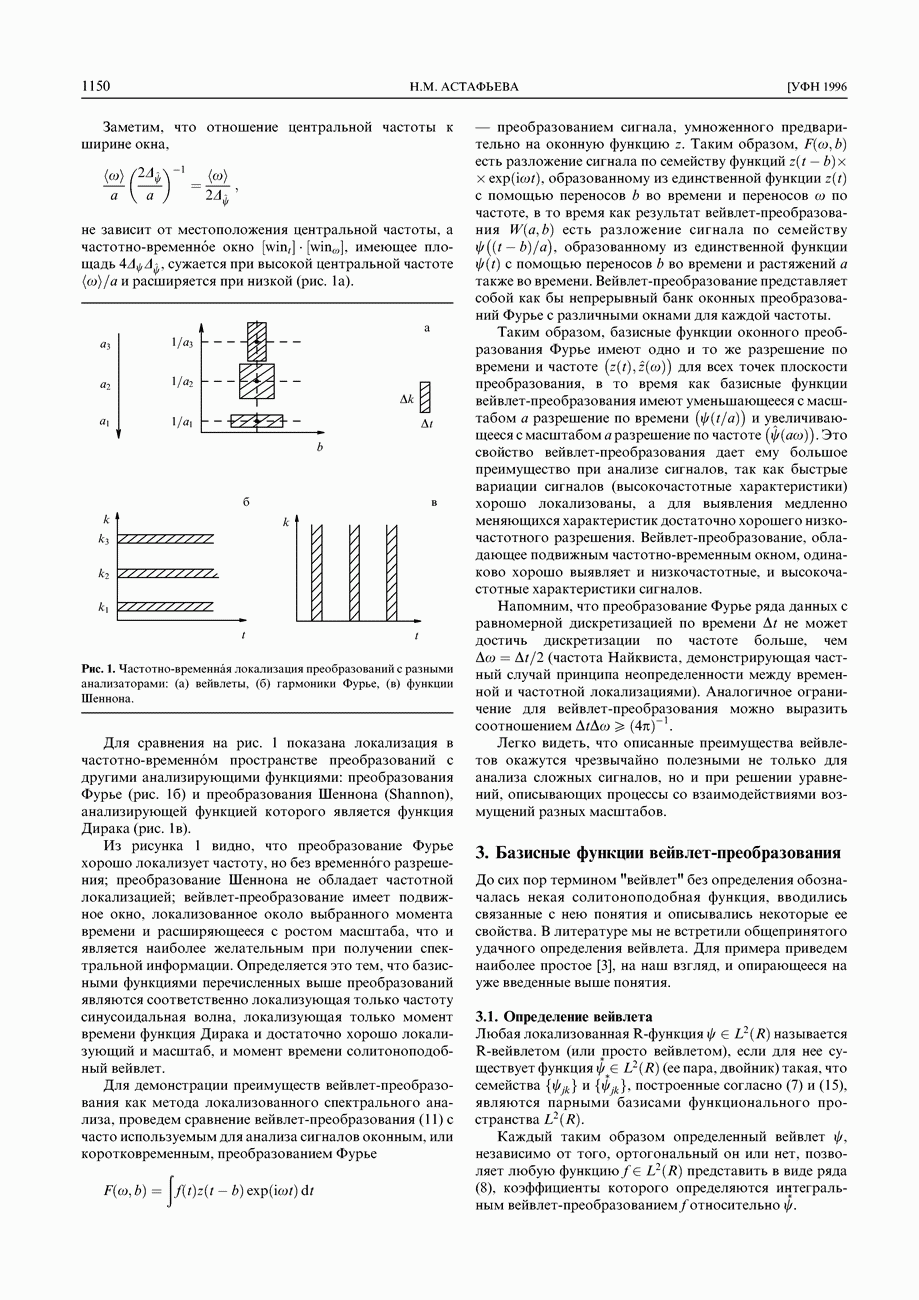
Рис. 3. Пример вейвлет-преобразования реального сигнала — потока ионов солнечного ветра: (а) анализируемый сигнал, (б) картина коэффициентов W(a,b), (в) картина линий локальных экстремумов, (г) зависимость коэффициентов W(a,b) от времени при значениях масштаба, отмеченных стрелками на (б), (д) распределение плотности энергии Ew(a, b) для фрагмента, взятого в рамку на (в).

На рисунке 36 темные области соответствуют положительным, а светлые — отрицательным значениям оттенками серого цвета в каждой из областей выделены диапазоны значений W(a,b). Ясно, что значение амплитуды вейвлет-преобразования в точке тем больше (по абсолютной величине), чем сильнее корреляция между вейвлетом данного масштаба и поведением сигнала в окрестности . Картина коэффициентов демонстрирует, что процесс составляют компоненты разных масштабов: экстремумы наблюдаются на разных масштабах, интенсивность их меняется и со временем, и с масштабом.

На рисунке 3в показана соответствующая картина линий локальных экстремумов — линий, от масштаба к масштабу соединяющих экстремумы каждой детали поверхности ("холма" или "впадины") отдельно. Многие авторы полагают, что скелетон не только четко и без лишних деталей визуализирует структуру анализируемого процесса, но de facto содержит всю информацию о нем. Сплошные линии на рисунке отмечают положение локальных максимумов точечные — минимумов.

Мы уже говорили, что вейвлет-преобразование разлагает анализируемый процесс на составляющие его волны, компоненты разного масштаба и, кроме того, дает "локализованную" во времени информацию о процессе. Горизонтальное сечение картины, приведенной на рис. 3б, при заданном масштабе а демонстрирует изменение компоненты выбранного масштаба со временем; на рис. 3г показано поведение трех компонент вблизи отмеченных на рис. 36 значений масштаба а. Вертикальное сечение картины коэффициентов в некоторый момент времени демонстрирует поведение процесса в окрестности выбранного момента времени (можно определить наличие и порядок особенности, набор задействованных масштабов, см. анализ локальной регулярности в разделе 4.3).

Обратим внимание на то, что значение анализируемой функции в точке влияет на значения коэффициентов преобразования в растущих с масштабом временных диапазонах, в так называемом углу влияния (рис. 4а). Ясно, что угол влияния выглядит иначе, если масштаб меняется не линейно, а по другому закону (логарифмическому, степенному).

Рис. 4. Угол влияния (а, б) и полоса влияния (в).

В свою очередь, коэффициент в точке зависит от значений части ряда из определяемого тем же углом влияния временного диапазона (диапазона интегрирования) около (рис. 46), и диапазон этот тем больше, чем больше масштаб т.е. высокочастотная (или мелкомасштабная) информация вычисляется на основе малых отрезков ряда, а низкочастотная — на основе больших.

Максимальный угол влияния (угол достоверности) отмечает область достоверности — область, вне которой коэффициенты вычисляются уже по отрезкам, выходящим за границы ряда (по дополненному ряду). Поскольку анализируемый ряд всегда конечен и необходимо получить максимум информации, полученные вне максимального угла влияния (с некоторой ошибкой) приближенные значения коэффициентов часто сохраняются. Для уменьшения ошибки ряд дополняется с учетом его поведения (средним значением, известным временным ходом и т.д.).

Вейвлет-преобразование может быть записано также через образы Фурье сигнала и вейвлета . Легко показать, что влияние компоненты Фурье испытывают коэффициенты находящиеся в горизонтальной полосе (рис. 4в); в свою очередь, на коэффициент в точке влияют все компоненты Фурье сигнала, для которых .

Раствор угла влияния и ширина полосы влияния зависят от базисного вейвлета. Так, например, используемый МНАТ-вейвлет (рис. 26) хорошо локализован во времени и имеет узкий энергетический спектр. Это удачное качество означает, в частности, что коэффициенты зависят от малого интервала области частот вейвлета, т.е. ширина полосы влияния невелика.

Вопросы, связанные с численными алгоритмами остаются за рамками работы. Приведем лишь несколько коротких и полезных, на наш взгляд, практических рекомендаций.

Дискретное вейвлет-преобразование очень хорошо приспособлено для быстрого численного алгоритма (см., например, [13]), использующего широко применяемую процедуру быстрого преобразования Фурье (FFT).

Непрерывное преобразование выполняется, как правило, прямым численным интегрированием. Самая простая (и быстрая) проверка численного алгоритма заключается в вычислении вейвлет-преобразования функции Дирака (в результате на каждом масштабе должен быть получен анализирующий вейвлет) или функции Гаусса (результат легко можно получить аналитически). Проверить достаточную плотность дискретизации по масштабу можно, вычислив вейвлет-преобразование самого анализирующего вейвлета и убедившись в отсутствии паразитных деталей.

Для дальнейшего анализа коэффициентов нам понадобится знание свойств вейвлет-преобразования. Все они следуют из изложенного уже в разделе 3 материала.