| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3. Фрактальное множество
Вейвлет-преобразование с его иерархическим базисом хорошо приспособлено для анализа каскадных процессов, турбулентных сигналов, фрактальных и мультифрактальных множеств, имеющих иерархическую природу.
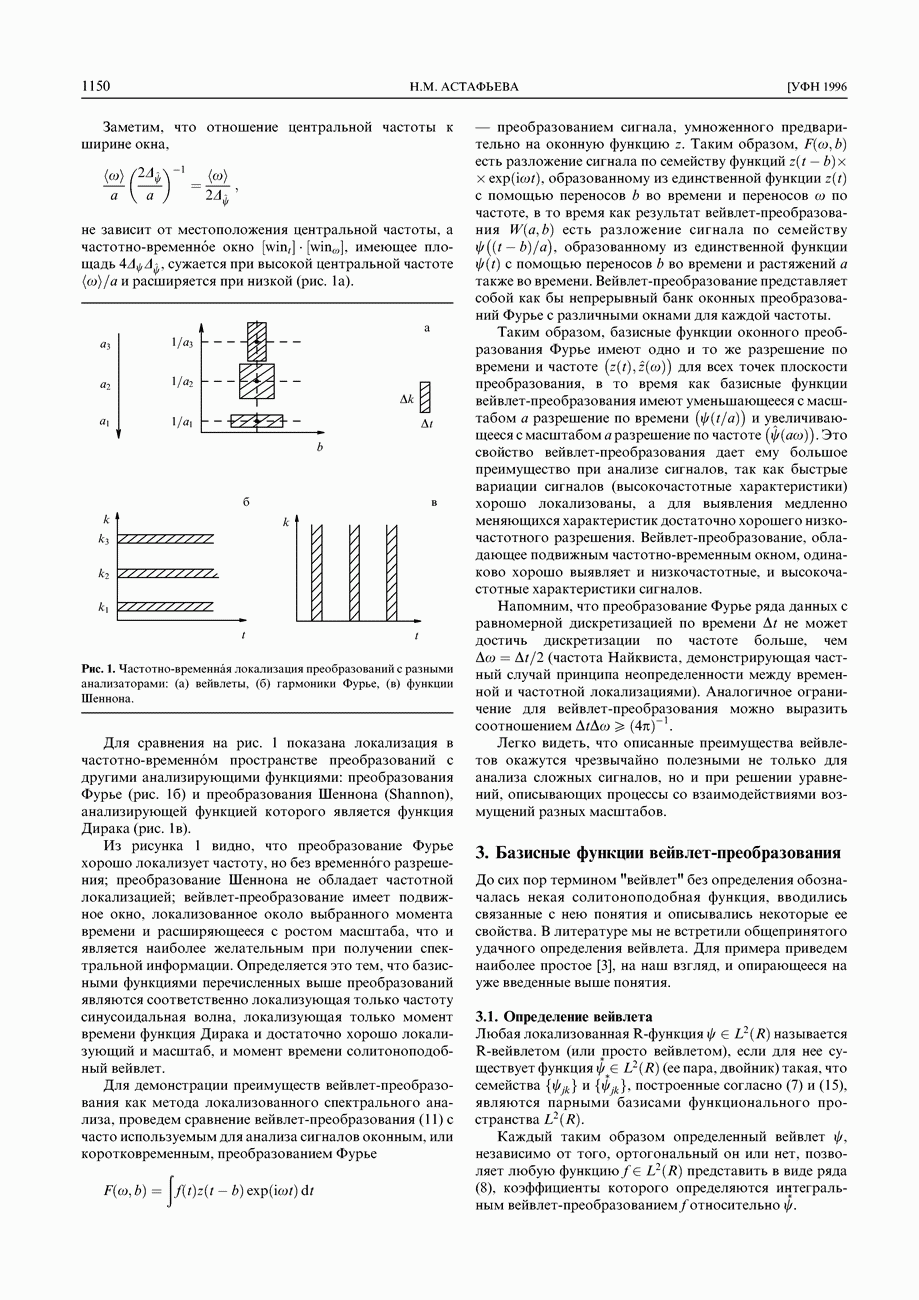
Приведем пример анализа фрактального множества, построенного на основе однородного триадного канторовского ряда. Как известно, при построении первого поколения этого ряда отрезок делится на три части, средняя из которых выбрасывается; при построении второго поколения такая же процедура проделывается с двумя оставшимися отрезками и так на каждом последующем этапе до бесконечности. На рисунке 12а показаны первые этапы построения ряда.
На основе получившегося множества — канторовской пыли — строится числовая последовательность, состоящая из нулей и единиц (нули соответствуют выбрасываемым при построении ряда частям отрезка).
На рисунке 126 показаны фрагменты картин коэффициентов и линий локальных максимумов. Они достаточно подробны, однако линейное изменение масштаба

Рис. 12. Первые поколения однородного триадного канторовского ряда (а), фрагменты картин коэффициентов и линий локальных максимумов (б); картины линий локальных максимумов триадного однородного канторовского ряда (в) и случайного процесса (г) в логарифмическом масштабе.
не позволяет охватить большой диапазон масштабов. Чтобы продемонстрировать общий характер процесса, на рис. 12в скелетон показан в логарифмическом масштабе.
Картина коэффициентов демонстрирует иерархическую структуру анализируемого множества. Еще более ясно она видна на картинах линий локальных максимумов. Скелетон выявляет не только иерархическую структуру анализируемого множества, но и способ построения фрактальной меры, на которой оно сформировано.
Каждый этап каскадного процесса, каждое дробление масштаба отмечено на картине локальных максимумов ветвлением, появлением характерной "вилочки" — линия, отмечающая положение локального максимума, раздваивается, расходясь на два независимых локальных максимума. Это неизменно повторяется, так как мера обладает свойством самоподобия и монофрактальна.
Известно, что фрактальная размерность или размерность подобия однородного канторовского ряда  где
где  — скорость ветвления,
— скорость ветвления,  — масштабный множитель. В случае триадного ряда
— масштабный множитель. В случае триадного ряда  Аналогично размерность вычисляется по коэффициентам вейвлет-преобразования как предел (при стремлении к нулю масштаба) отношения
Аналогично размерность вычисляется по коэффициентам вейвлет-преобразования как предел (при стремлении к нулю масштаба) отношения  ; здесь
; здесь  — число локальных максимумов. Чем более высокого порядка поколение канторовского ряда используется, тем точнее определяется его размерность; для 10-го, 11-го поколения вычисленное по коэффициентам вейвлет-преобразования значение размерности практически совпадает с теоретическим.
— число локальных максимумов. Чем более высокого порядка поколение канторовского ряда используется, тем точнее определяется его размерность; для 10-го, 11-го поколения вычисленное по коэффициентам вейвлет-преобразования значение размерности практически совпадает с теоретическим.
Для сравнения на рис. 12г представлены линии локальных максимумов случайного процесса. Видно, насколько даже качественно различаются "древовидная" структура скелетона каскадного процесса и "тра-вовидный" скелетон случайного (можно сравнить с периодическими скелетами гармонических функций и "кустами" линий, отмечающими особенности сигналов).
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
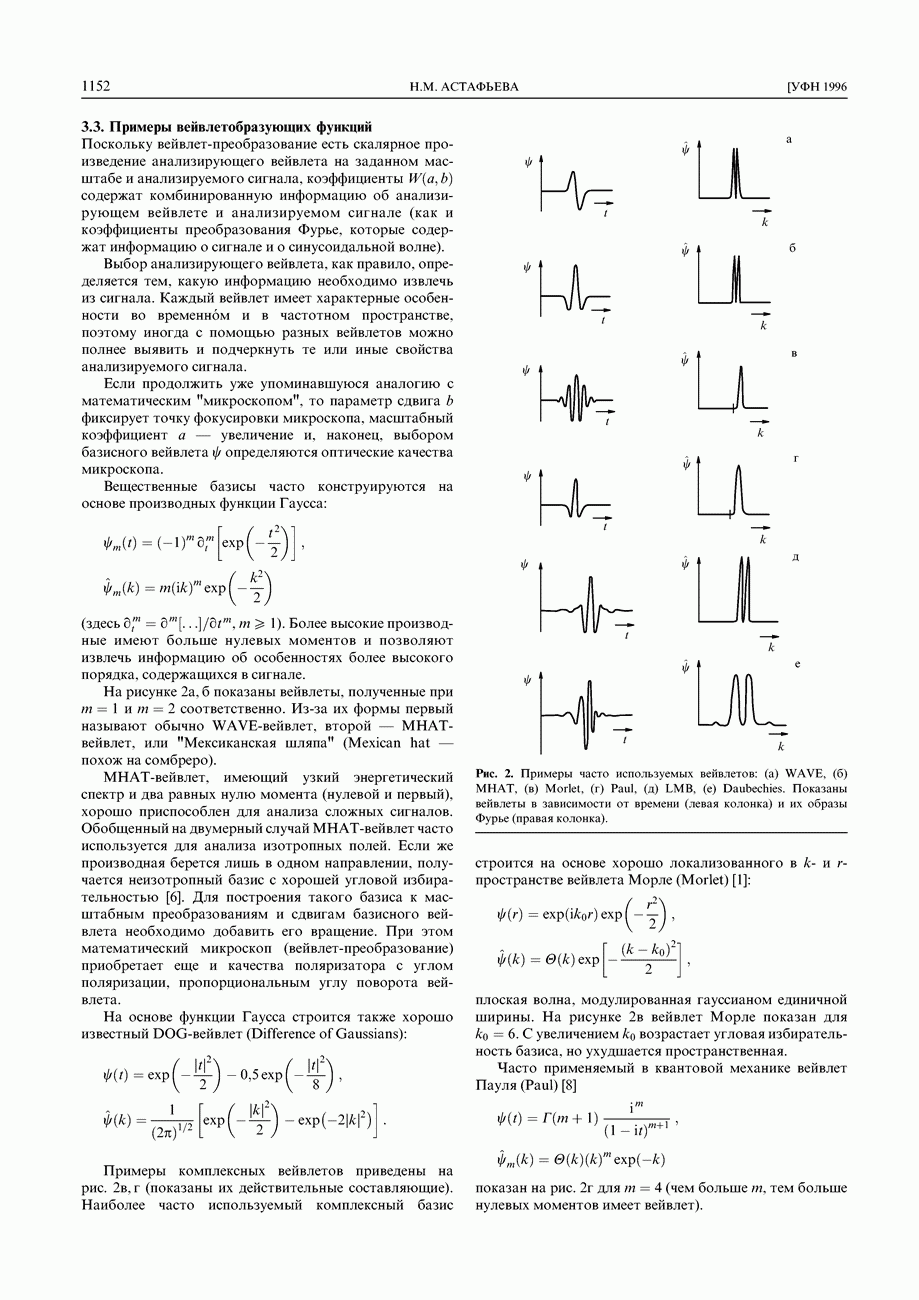
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы