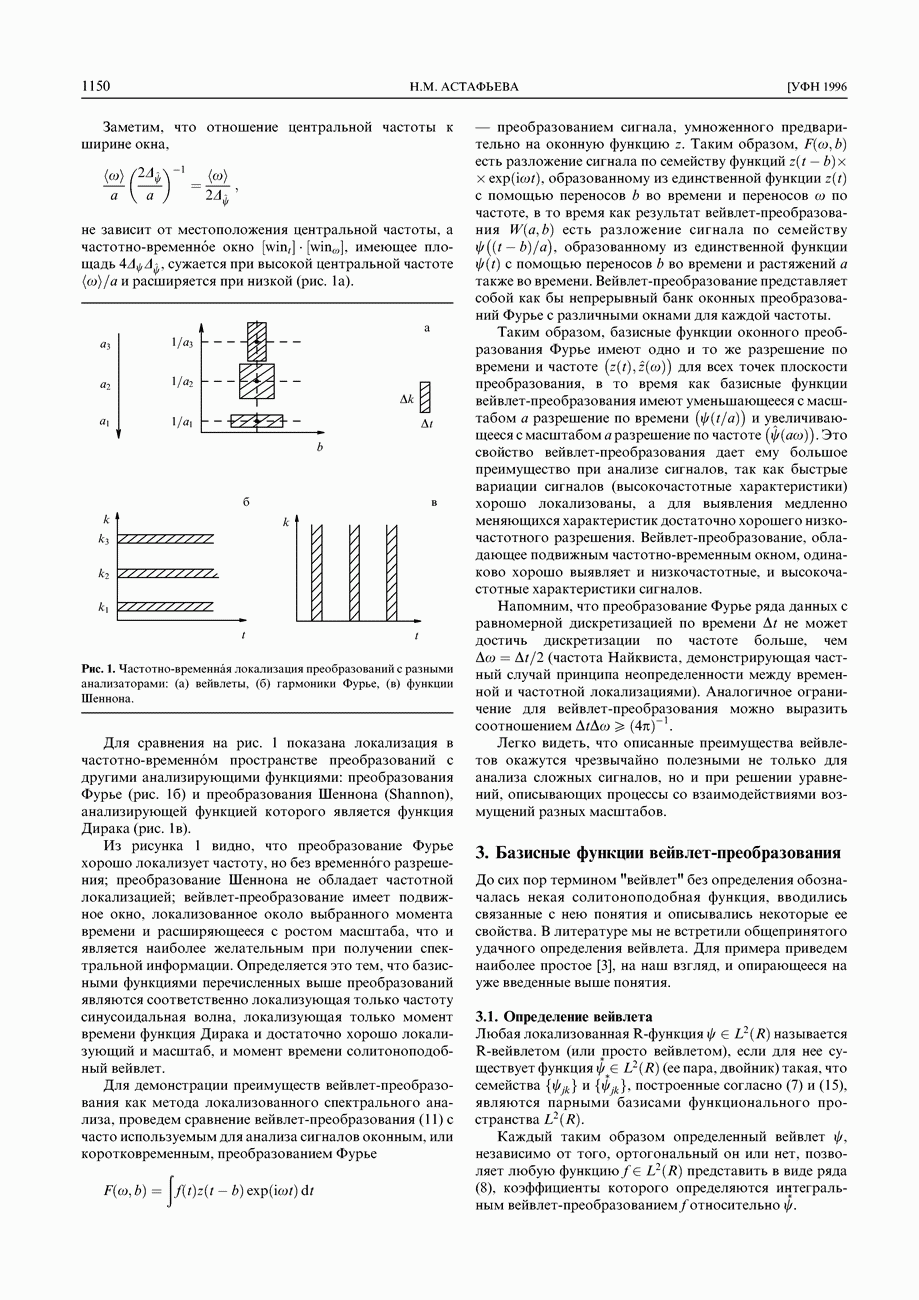
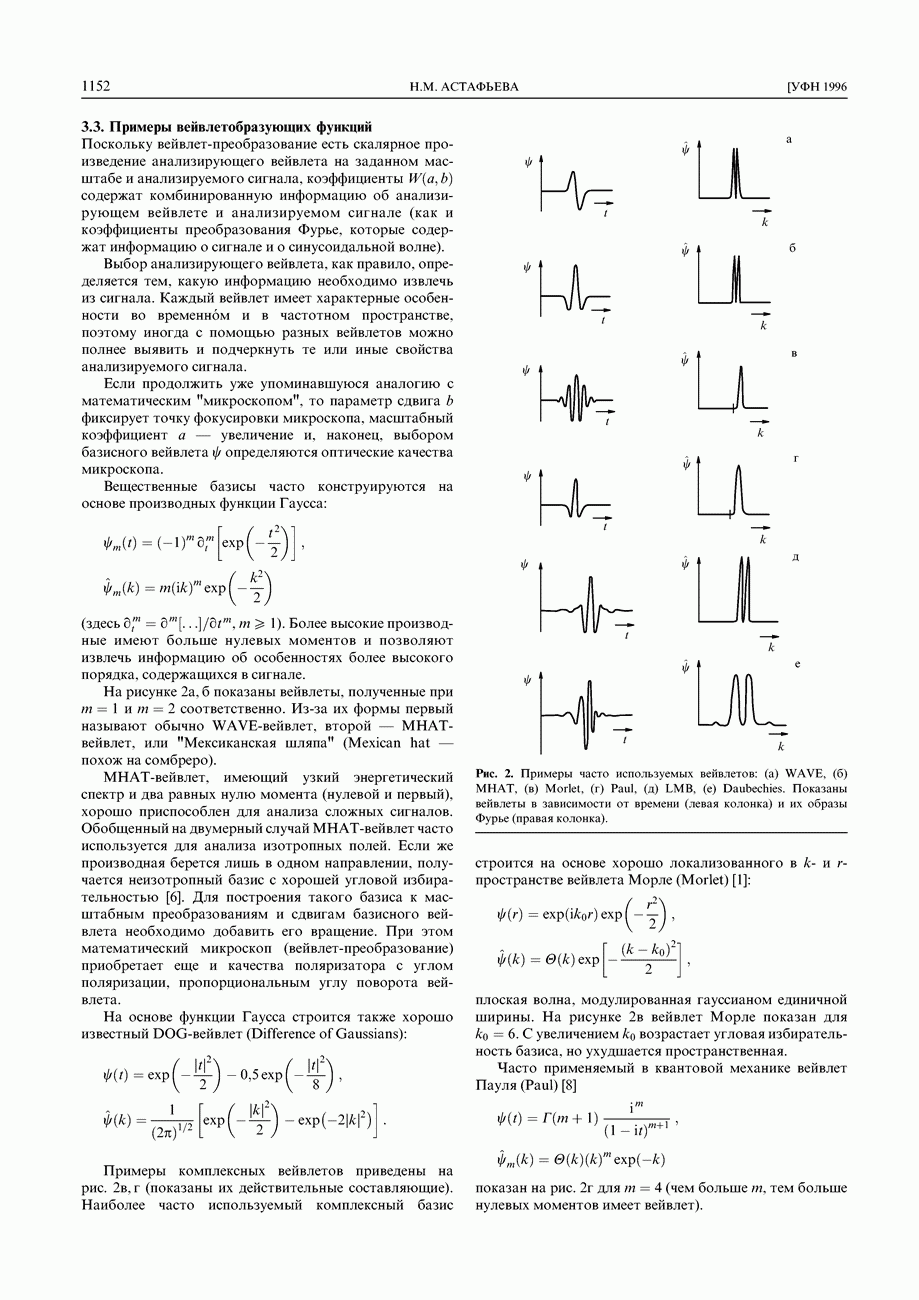
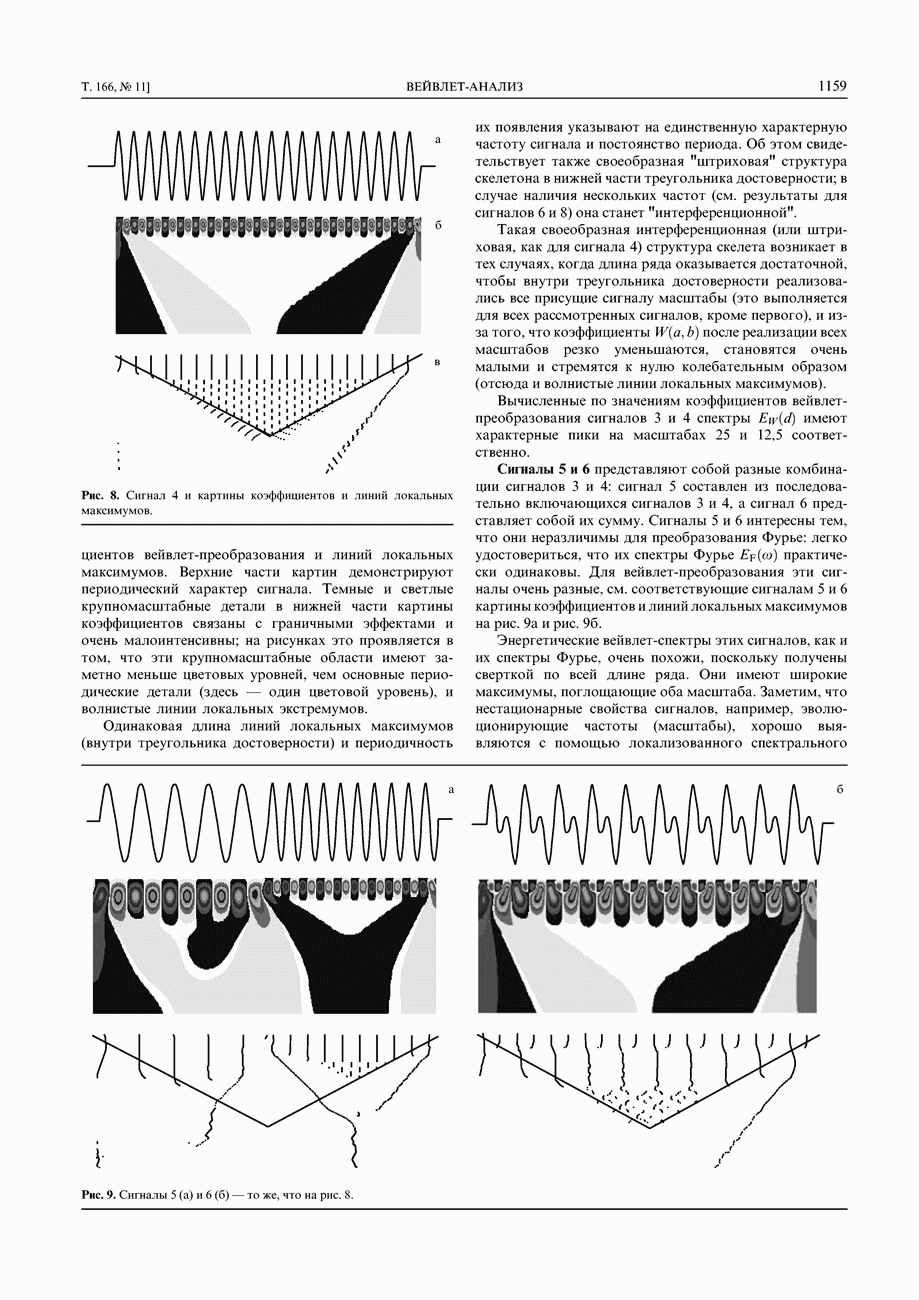
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Свойства вейвлет-преобразования
Мы уже говорили, что коэффициенты вейвлет-преобразования содержат комбинированную информацию об анализирующем вейв лете и анализируемом сигнале. Несмотря на это, вейвлет-анализ позволяет получить и объективную информацию об анализируемом сигнале, так как некоторые свойства вейвлет-преобразования не зависят от выбора анализирующего вейвлета. Независимость от анализатора делает эти простые свойства преобразования очень важными.
Выпишем основные элементарные свойства вейвлет-преобразования функции f(t). Будем использовать обозначение  .
.
Линейность:

Отсюда, в частности, следует, что вейвлет-преобразование векторной функции есть вектор с компонентами, представляющими собой вейвлет-преобразование каждой из компонент анализируемого вектора в отдельности.
Инвариантность относительно сдвига:

Из этого свойства следует коммутативность дифференцирования, в частности,  (здесь
(здесь  ). Вместе с первым свойством это означает перестановочность и для производных векторного анализа.
). Вместе с первым свойством это означает перестановочность и для производных векторного анализа.
Инвариантность относительно растяжения (сжатия):

Это свойство позволяет, в частности, определять наличие и характер особенностей анализируемой функции (см. раздел 4.3.1).
Кроме трех выписанных не зависящих от выбора анализирующего вейвлета элементарных свойств вейвлет-преобразование обладает еще несколькими. Наиболее важными и полезными из них, на наш взгляд, являются следующие.
Частотно-временная локализация и наличие частотно-временного окна и угла влияния (правильнее было бы говорить о масштабно-временной локализации). Параметры частотно-временного окна выписаны в разделе 2.4.
Дифференцирование:

Таким образом, чтобы проигнорировать, например, крупномасштабные полиномиальные составляющие и проанализировать особенности высокого порядка или мелкомасштабные вариации функции  безразлично, дифференцировать ли нужное число раз анализирующий вейвлет или саму функцию. Это очень полезное свойство, если учесть, что часто функция
безразлично, дифференцировать ли нужное число раз анализирующий вейвлет или саму функцию. Это очень полезное свойство, если учесть, что часто функция  представляет собой ряд чисел, а анализирующий вейвлет задан формулой.
представляет собой ряд чисел, а анализирующий вейвлет задан формулой.
Для вейвлет-преобразования существует аналог теоремы Парсеваля и выполняется равенство

откуда следует, что энергия сигнала может быть вычислена через амплитуды (коэффициенты) вейвлет-преобразования подобно тому, как она вычисляется через амплитуды преобразования Фурье:

Определения и свойства одномерного непрерывного вейвлет-преобразования обобщаются на многомерный и на дискретный случаи. Каждый из них имеет свои особенности. Здесь мы не будем о них говорить, поскольку для дальнейшего нам понадобится непрерывное вейвлет-преобразование одномерных функций.
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы