| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.3. Среднемесячные значения индекса Южного Колебания
Напомним, что индекс Южного Колебания  — это определенным образом нормированная разность атмосферного давления, измеряемого на уровне моря на станциях, расположенных вблизи центров действия
— это определенным образом нормированная разность атмосферного давления, измеряемого на уровне моря на станциях, расположенных вблизи центров действия
Южного Колебания. Обычно он вычисляется следующим образом. Берутся временные ряды давления станций Таити и Дарвина  (индексы
(индексы  обозначают год и месяц). По ним вычисляются ряды нормализованного давления станций
обозначают год и месяц). По ним вычисляются ряды нормализованного давления станций  здесь
здесь  — среднее многолетнее значение (норма), вычисленное по среднемесячным данным за период 1951-1980 гг.; в — стандартное отклонение, вычисленное по всем значениям аномалий давления за период 1951-1980 гг. Затем вычисляются нормализованные аномалии давления станций Таити (индекс Т) и Дарвина (индекс D)
— среднее многолетнее значение (норма), вычисленное по среднемесячным данным за период 1951-1980 гг.; в — стандартное отклонение, вычисленное по всем значениям аномалий давления за период 1951-1980 гг. Затем вычисляются нормализованные аномалии давления станций Таити (индекс Т) и Дарвина (индекс D)  , наконец, вычисляются значения индекса Южного Колебания:
, наконец, вычисляются значения индекса Южного Колебания:  — стандартное отклонение всех разностей
— стандартное отклонение всех разностей  за тот же базовый период времени с 1951-го по 1980 гг.). Отрицательные значения этого индекса тесно связаны с событиями Эль-Ниньо, положительные, соответственно, с Ла-Ниньа.
за тот же базовый период времени с 1951-го по 1980 гг.). Отрицательные значения этого индекса тесно связаны с событиями Эль-Ниньо, положительные, соответственно, с Ла-Ниньа.
На рисунке 14 представлены изменение среднемесячных значений индекса  за последние 108 лет (рис. 14а) и картина коэффициентов вейвлет-преобразования (рис. 14б) в таком диапазоне масштабов, чтобы охватить по возможности все крупномасштабные детали процесса, описываемые этим конечным рядом (масштаб линейно растет вниз до 97 лет). На рисунке 14в представлено распределение плотности энергии среднемесячных значений индекса
за последние 108 лет (рис. 14а) и картина коэффициентов вейвлет-преобразования (рис. 14б) в таком диапазоне масштабов, чтобы охватить по возможности все крупномасштабные детали процесса, описываемые этим конечным рядом (масштаб линейно растет вниз до 97 лет). На рисунке 14в представлено распределение плотности энергии среднемесячных значений индекса  в более мелкомасштабной области, масштаб меняется до 10,5 лет.
в более мелкомасштабной области, масштаб меняется до 10,5 лет.
Обращают на себя внимание два крупномасштабных минимума почти на границах ряда и ветвящееся "дерево"

Рис. 14. Среднемесячные значения индекса Южного Колебания (а), картина коэффициентов (б), картина распределения плотности энергии (в), а также картина коэффициентов (г) для фрагмента, взятого в рамку на рис. б.
положительных экстремумов между ними. Ствол дерева и две его почти одновременно начинающиеся ветви выделяют два практически одинаковых периода — между Эль-Ниньо на границах дерева и в его середине по 39,8 лет (что согласуется с масштабом около 40 лет для 500-летних данных и свидетельствует в пользу существования 75-80-летнего цикла).
Распределение плотности энергии (рис. 14в) показывает, что мелкомасштабная часть процесса демонстрирует наличие диапазонов локальных периодичностей и, кроме того, качественное отличие структуры процесса в отрезки времени, принадлежащие и не принадлежащие дереву. Внутренняя часть дерева содержит, в основном, детали с характерными масштабами около 30 и 12 месяцев, а внешние части дерева составлены, в основном, из деталей с масштабом около 18 месяцев.
Возможно, наличием эпох с разной временной структурой можно объяснить отмечаемое многими авторами изменение характера сценариев Эль-Ниньо после середины 70-х годов. В этой связи следует сказать, что при изучении процесса ЮКЭН (и, возможно, не только ЮКЭН) не следует делать слишком категорических выводов, опираясь в анализе на наблюдения в течение последних нескольких десятилетий. Необходим анализ гораздо более представительных данных (в нашем случае, например, ряды наблюдений за последние 30 лет оказались бы недостаточными).
Однако вернемся к структуре картины коэффициентов. Два крупномасштабных минимума на границах дерева и один между его ветвями соответствуют интенсивным и продолжительным явлениям Эль-Ниньо 1899-1902,1940-1941 и 1982-1983 годов. При сравнении с 500-летними данными можно убедиться, что эти сильнейшие за последнее столетие Эль-Ниньо являются вполне ординарными событиями. Несмотря на то что 500-летние данные не содержат информации об интенсивности процесса и усреднены по 12 месяцам, детали картин хорошо согласуются. Можно считать, что реконструированная за последние 500 лет хронология событий Эль-Ниньо неплохо описывает динамику Южного Колебания на больших временах (порядка нескольких десятилетий).
Более подробно ветви дерева показаны на рис. 14г: здесь масштаб растет до 29 лет. Картины коэффициентов (и линий локальных максимумов) демонстрируют непростую иерархическую структуру. Если в основании дерева мы отметили укрупнение масштаба в виде удвоения периода, то уже две главные ветви дерева ветвятся по-разному — левая на три, а правая на две ветви. На более мелких масштабах продолжается, как кажется, нерегулярное чередование удвоения и утроения линий локальных максимумов. Встречаются и ветвления типа водораздела, когда в главную линию локальных максимумов по мере роста масштаба вливаются последовательно несколько побочных.
Внешне похожие ветвления можно смоделировать канторовским множеством, когда из единичного отрезка (у нас это примерно 80 лет) удаляется средняя треть, из оставшихся частей также удаляются средние трети и т.д. (модель удвоения линий локальных максимумов); или удаляются две из пяти частей единичного отрезка и т.д. в каждом следующем поколении из каждой части (модель утроения).
В нашем случае процесс сложнее по крайней мере в двух отношениях. Во-первых, встречаются чередующиеся нерегулярным образом ветвления двух (или даже более) типов — так устроены неоднородные или мультифрактальные множества. Во-вторых, в отличие от стандартной процедуры построения канторовского множества, где раз удаленная часть отрезка не восстанавливается ни в какой своей части, здесь продолжаются ветвления линий локальных экстремумов обоих знаков, т.е. в удаленном отрезке на следующих этапах как бы восстанавливаются некоторые его части. Будет ли результатом такого каскадного процесса канторовская пыль или иное фрактальное множество, зависит от совокупности правил ветвления, выяснить которые по ограниченному ряду данных затруднительно.
Таким образом, вейвлет-анализ ряда среднемесячных значений индекса Южного Колебания выявил автомодельную структуру данных и наличие подобного каскадному процесса на масштабах от месяца до нескольких десятилетий (до 70-80 лет). Является ли полученная древовидная картина линий локальных максимумов свидетельством того, что система демонстрирует каскад увеличений (удвоений, утроений и т.д.) периода, квазипериодическое или иное поведение, является ли продолжающееся на малых временных масштабах ветвление линий локальных экстремумов обоих знаков свидетельством наличия каскадного процесса на масштабах порядка месяца и менее, покажут дальнейшие исследования; для этого необходим, в частности, анализ рядов с более мелким разрешением.
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
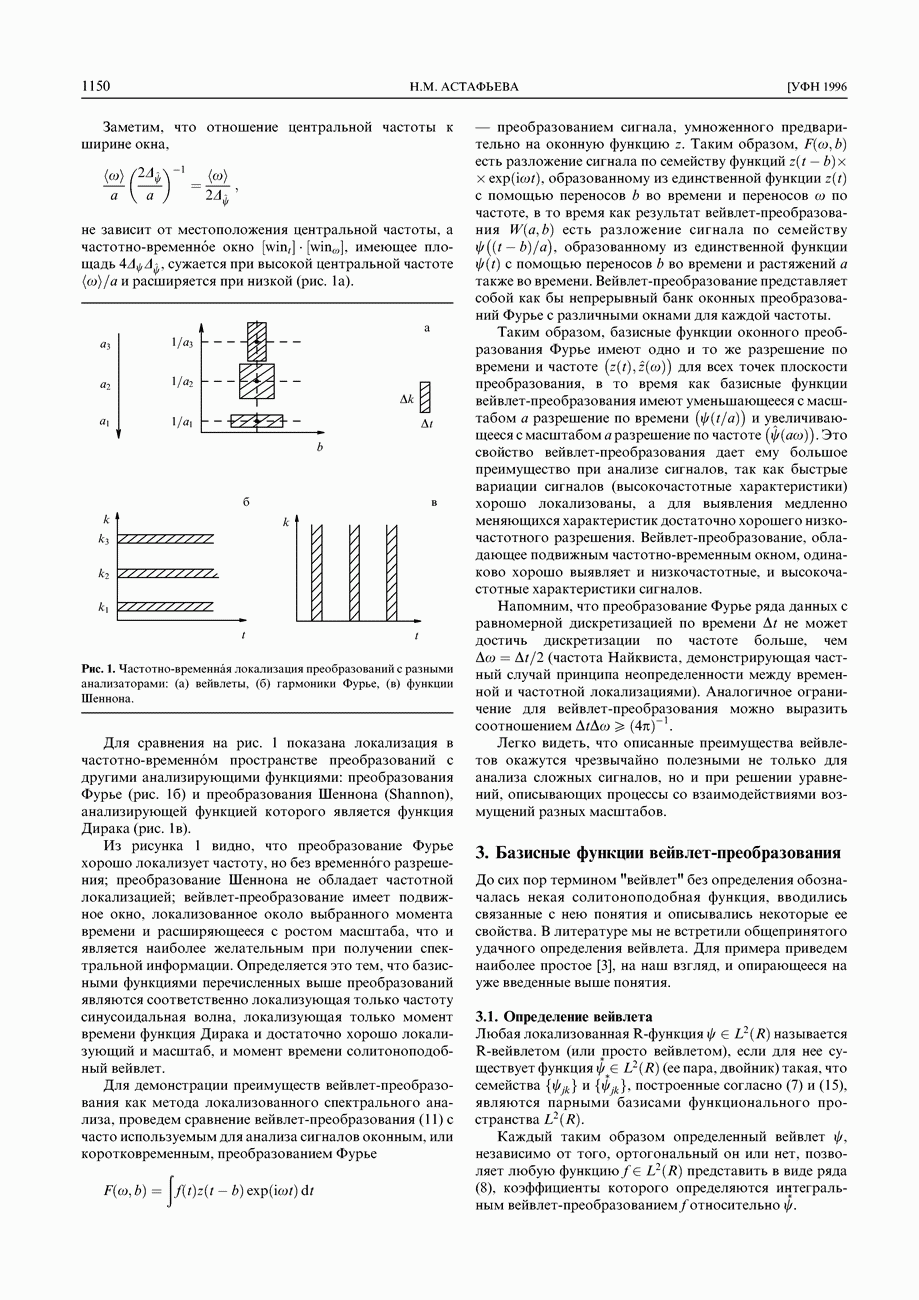
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
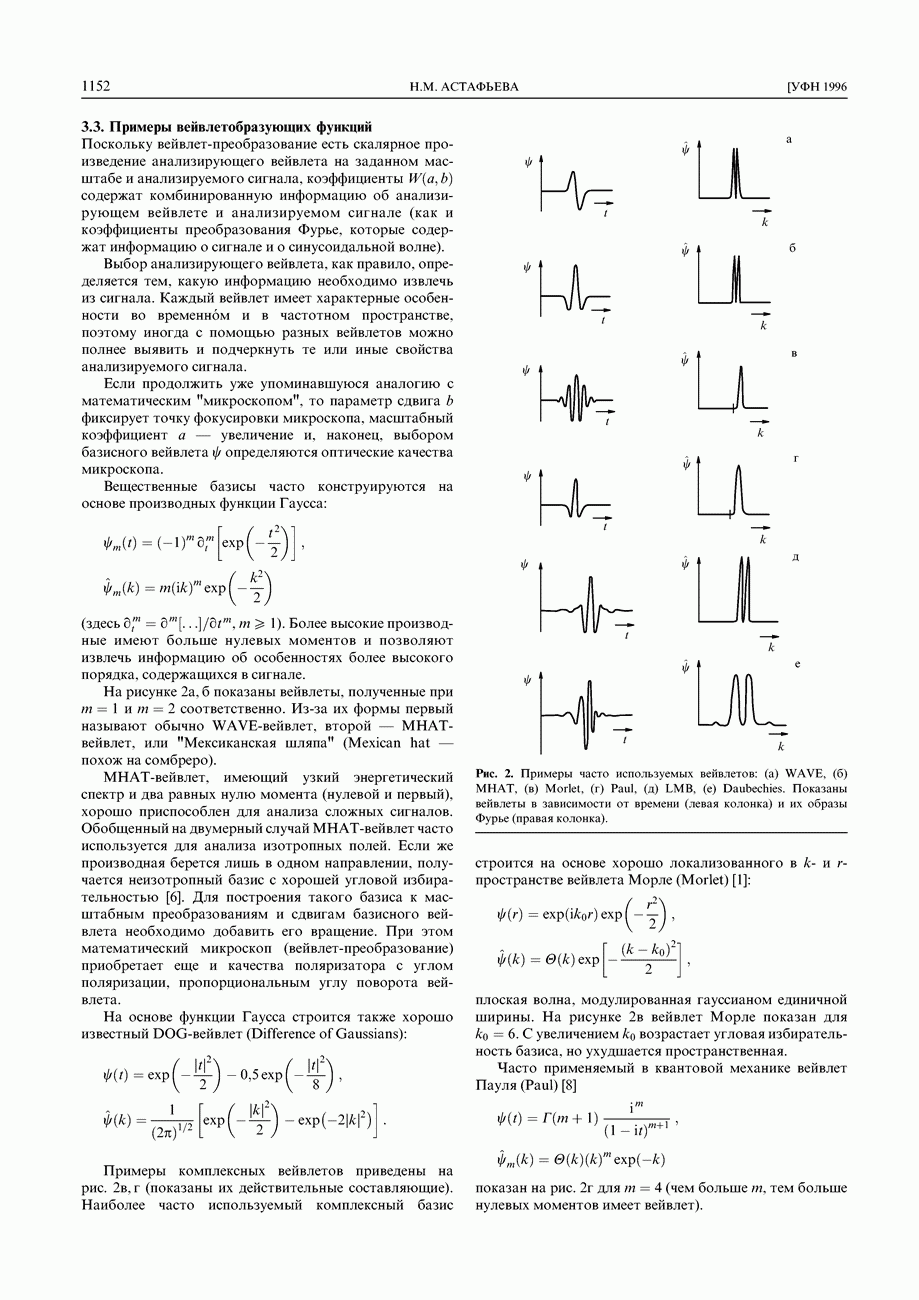
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы