| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Сигнал с особенностью
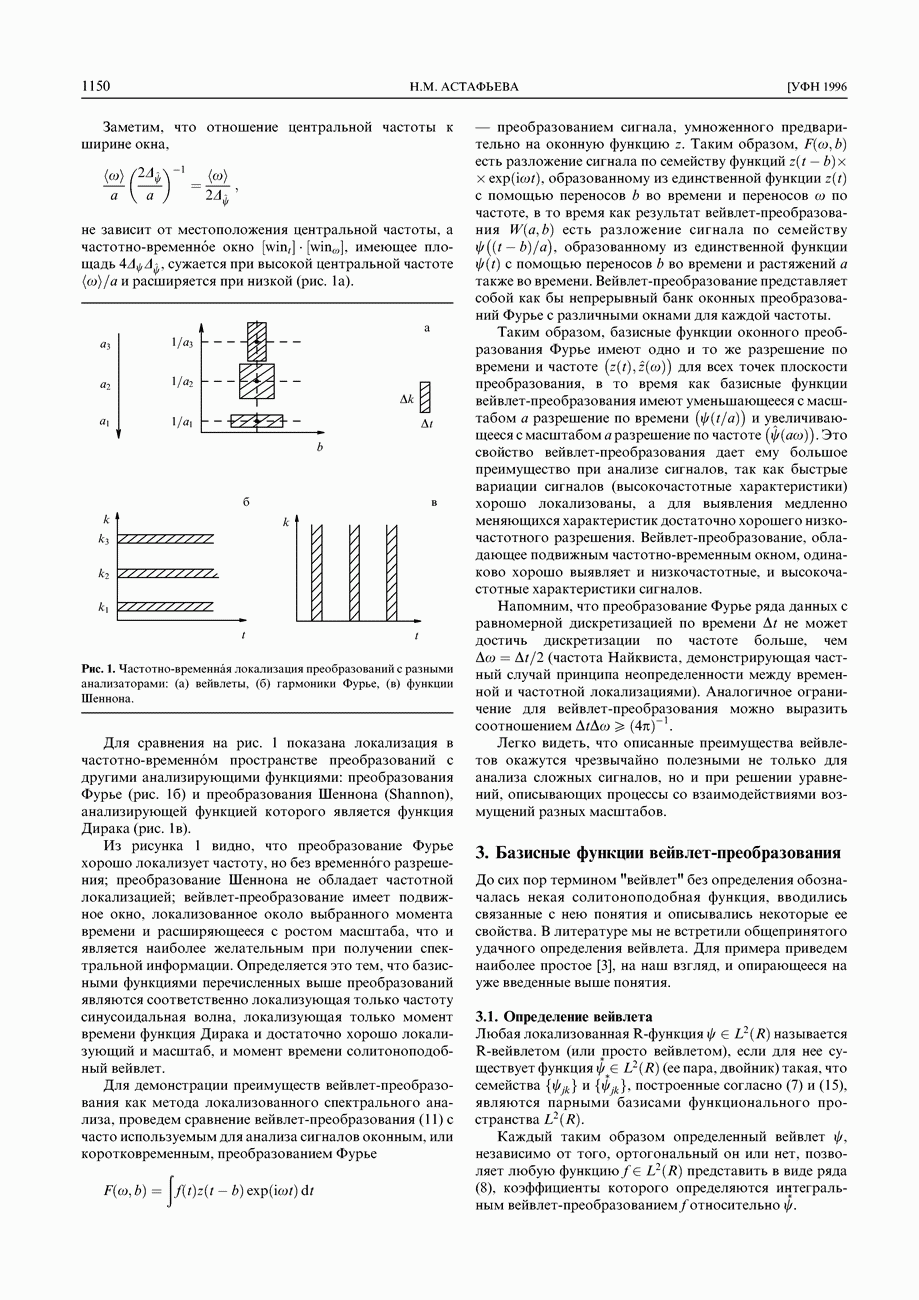
В сигналах часто встречаются изолированные особенности типа импульса, ступеньки, степенные особенности и т.п. Это могут быть как присущие описываемому сигналом процессу детали, так и паразитные детали, например, сбои аппаратуры. Преобразование Фурье сигнала, регулярного везде за исключением одной сбойной точки, несет информацию о ней во всех своих коэффициентах. Изолированные особенности практически не фильтруются, искажая спектр и реконструированный сигнал.
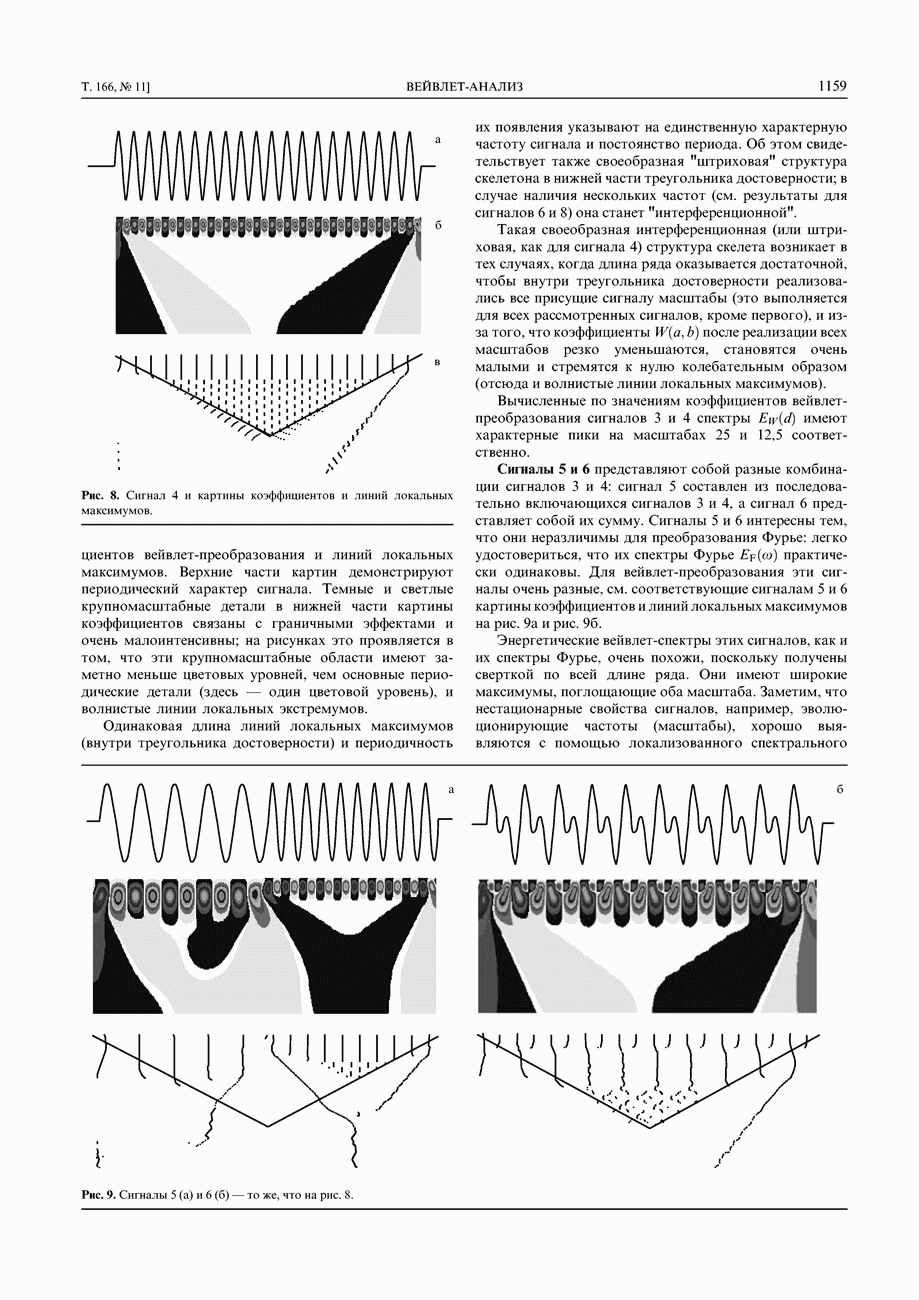
Вейвлет-преобразование применялось к сигналам с особенностями некоторых из перечисленных типов. На рисунке 11 кроме сигналов представлены картины линий локальных экстремумов (они более характерны) и схематически изображены несколько линий уровня значений коэффициентов W(a,b) (сплошные линии относятся к положительным, штриховые — к отрицательным значениям).

Рис. 11. Вейвлет-преобразование сигнала с особенностями:  - функция,
- функция,  скачок, излом (слева направо).
скачок, излом (слева направо).
Все точечные особенности, содержащиеся в сигналах, сопровождаются линиями локальных максимумов, исходящими из этих точек. Количество их определяется характером особенности сигнала и анализирующим вейв летом.
Примеры в разделе 5.1 показали, что смена знака производной анализируемой функции отмечается линией локальных экстремумов распределения 
На рисунке 11а показано преобразование сигнала с особенностью типа  -функции. Следующие два примера (рис. 11б, в) содержат особенности, при которых смена знака производной сопровождается разрывом функции (степенные особенности вида
-функции. Следующие два примера (рис. 11б, в) содержат особенности, при которых смена знака производной сопровождается разрывом функции (степенные особенности вида  соответственно). В этом случае точка локализации особенности сигнала отмечена тремя линиями скелетона. Центральная линия является линией максимумов или минимумов в зависимости от того, имеет ли сигнал в этой точке максимум или минимум. Аналогично выглядят результаты вейвлет-преобразования
соответственно). В этом случае точка локализации особенности сигнала отмечена тремя линиями скелетона. Центральная линия является линией максимумов или минимумов в зависимости от того, имеет ли сигнал в этой точке максимум или минимум. Аналогично выглядят результаты вейвлет-преобразования  -функции.
-функции.
Особенности менее высокого порядка, такие, как перегиб функции  (рис. 11г) или скачок (рис. 11д), отмечаются двумя линиями локальных экстремумов, излом (рис. 11e) — одной.
(рис. 11г) или скачок (рис. 11д), отмечаются двумя линиями локальных экстремумов, излом (рис. 11e) — одной.
Таким образом, вейвлет-преобразование способно выявить положение особенности — коэффициенты вейвлет-преобразования гладкой функции малы и резко возрастают при появлении особенности, отмечая ее локализацию линиями локальных экстремумов. Характер особенности в точке определяется из асимптотического поведения коэффициентов вейвлет-преобразования при стремлении масштаба к нулю. Например, значения коэффициентов вейвлет-преобразования  -функции максимальны на малых масштабах, а с ростом масштаба резко убывают, повторяя характер особенности. Изолированная особенность локальным образом влияет на коэффициенты вейвлет-преобразования и при необходимости может быть легко удалена из сигнала или скорректирована.
-функции максимальны на малых масштабах, а с ростом масштаба резко убывают, повторяя характер особенности. Изолированная особенность локальным образом влияет на коэффициенты вейвлет-преобразования и при необходимости может быть легко удалена из сигнала или скорректирована.
Приведенные результаты получены с помощью МНАТ-вейвлета, имеющего два равных нулю момента (нулевой и первый). Вейвлеты же, имеющие только один нулевой момент, неспособны различать особенности производных. Распределение коэффициентов вейвлет-преобразования, полученное с помощью такого вейвлета, имеет меньше линий локальных экстремумов. Например, для первых трех сигналов, отсутствует центральная линия экстремумов; особенность производной сигнала с перегибом (рис. 11г) не отмечена вообще, а скачок (рис. 11 в) сигнала отмечен одной линией экстремума.
Чем выше порядок анализирующего вейвлета, чем больше нулевых моментов он имеет, тем лучше вейвлет-преобразование дифференцирует особенности.
Отметим, что вейвлет-преобразование с вейвлетами разного порядка с успехом может быть использовано для выявления наличия и характера наиболее крупномасштабной составляющей сигнала — так называемого тренда. Применив к коэффициентам реконструкционную формулу и вычтя реконструированный сигнал из исходного, можно выделить ту самую крупномасштабную составляющую, которая обращается в нуль вследствие наличия нулевых моментов у вейвлета: постоянная составляющая, линейный или полиномиальный тренд и т.п. Таким образом, устраняется элемент субъективизма, который почти всегда присутствует при определении тренда другими способами.
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
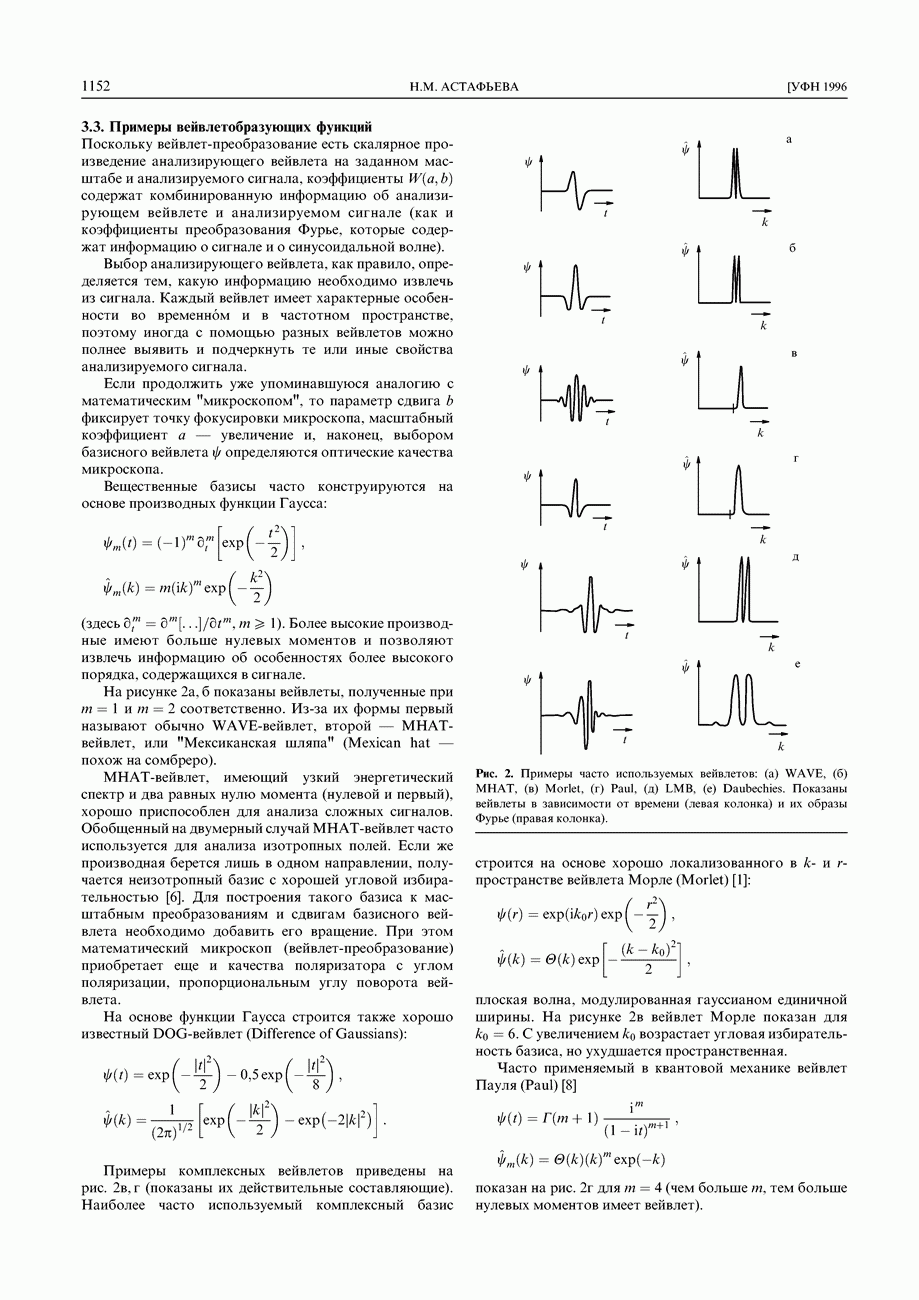
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы