| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
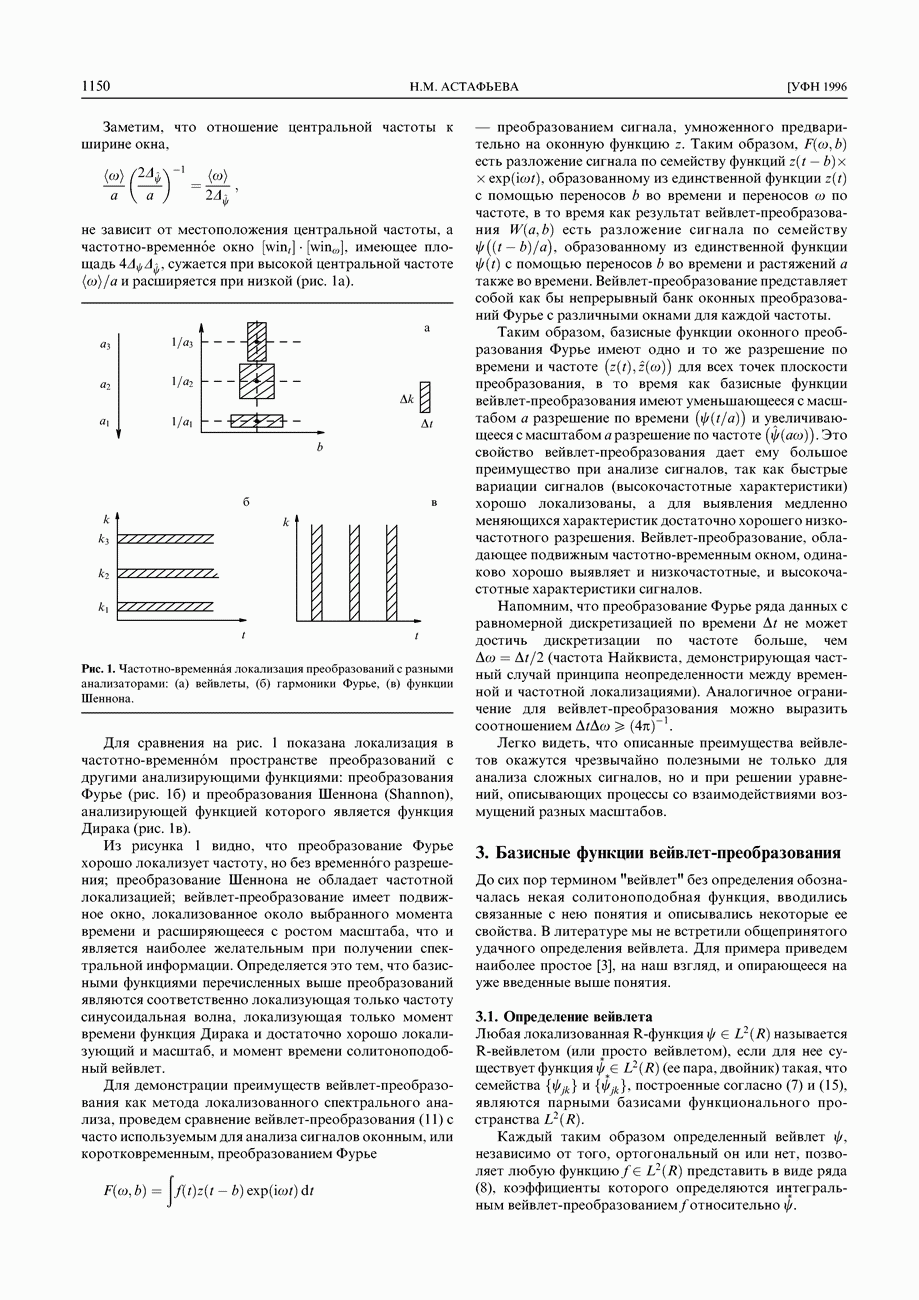
5. Применение вейвлет-преобразования к модельным сигналам
В этом разделе показаны некоторые возможности вейвлет-преобразования в выявлении различных характерных особенностей сигналов. Вейвлет-преобразование применяется к модельным сигналам, построенным на основе функций с хорошо известными свойствами (см. также [17]).
Для каждого примера приведен график анализируемого ряда. Коэффициенты  показаны в виде проекций на плоскость
показаны в виде проекций на плоскость  (временной масштаб, время); по оси абсцисс отложено время, по оси ординат — временной масштаб (он линейно растет вниз). Как и на рис. 3б, светлые области соответствуют положительным, а темные — отрицательным значениям
(временной масштаб, время); по оси абсцисс отложено время, по оси ординат — временной масштаб (он линейно растет вниз). Как и на рис. 3б, светлые области соответствуют положительным, а темные — отрицательным значениям  оттенками серого цвета в каждой области выделены диапазоны значений
оттенками серого цвета в каждой области выделены диапазоны значений  Картины линий локальных экстремумов или локальных максимумов представлены в тех же координатах.
Картины линий локальных экстремумов или локальных максимумов представлены в тех же координатах.
Приведенные результаты получены с помощью МНАТ-вейвлета. Вычисления проводились в прямоугольной области значений параметров  Ряды данных для этого продлевались; способ дополнения показан на графиках анализируемых функций. На картинах линий локальных максимумов показан треугольник достоверности, или максимальный угол влияния.
Ряды данных для этого продлевались; способ дополнения показан на графиках анализируемых функций. На картинах линий локальных максимумов показан треугольник достоверности, или максимальный угол влияния.
5.1. Гармоническая функция
Вейвлет-преобразование применялось к рядам синусоид

Результаты вейвлет-преобразования такой функции легко сравнить с теми, что дает привычное преобразование Фурье. Значения периодов  и постоянной
и постоянной  анализируемых сигналов приведены в табл. 1. В нее занесены также номер соответствующего рисунка и
анализируемых сигналов приведены в табл. 1. В нее занесены также номер соответствующего рисунка и
номер сигнала. По коэффициентам вейвлет-преобразования должны быть получены масштабы  .
.
Таблица 1. Параметры гармонических функций

Сигнал 1. На рисунке 6а показан сигнал — сумма синусоид с заметно отличающимися частотами (как видно из графика, ряд продолжен средним значением).
На картине значений коэффициентов (рис. 6б) легко различаются многочисленные периодически повторяющиеся детали в верхней части картины (при малых значениях масштаба а), являющиеся результатом резонанса высокочастотной составляющей сигнала с мелкомасштабными вейвлетами; а также три темные и две светлые области на крупных масштабах (положительные и отрицательные значения  соответственно), являющиеся результатом сильной корреляции между крупномасштабными вейвлетами и низкочастотной составляющей сигнала, представленной всего двумя с половиной периодами.
соответственно), являющиеся результатом сильной корреляции между крупномасштабными вейвлетами и низкочастотной составляющей сигнала, представленной всего двумя с половиной периодами.

Рис. 6. Сигнал 1 (а) и результаты его вейвлет-преобразования: картины коэффициентов (б), линий локальных экстремумов (в) и линий локальных максимумов (г).
На рисунке 6в представлены линии локальных экстремумов; сплошные линии отмечают локальные максимумы, точечные — локальные минимумы. На картине локальных максимумов (рис. 6г) показаны только линии, относящиеся к положительным экстремумам. Обе картины выявляют периодическую структуру анализируемого сигнала и представляют собой масштабно-временной скелет описываемого сигналом процесса. Линии, отмечающие положение локальных экстремумов коэффициентов вейвлет-преобразования, соответствуют экстремумам анализируемой функции — точкам смены знака ее производной.
В дальнейшем будет демонстрироваться лишь один из скелетонов; если линии локальных минимумов не несут смысловой нагрузки и лишь усложняют рисунок, как для сигнала 1, то будет представлена только картина линий локальных максимумов.
Сигнал 2 представляет собой часть сигнала 1. Картина коэффициентов вейвлет-преобразования позволяет говорить о крупномасштабной составляющей в сигнале, даже если на длине сигнала уложился всего один период крупномасштабной составляющей сигнала 1.
Энергетический спектр  позволяет в этом простом случае определить даже масштаб крупномасштабной составляющей сигнала, хотя она и представлена всего одним периодом. На рисунке 7 показан спектр энергии
позволяет в этом простом случае определить даже масштаб крупномасштабной составляющей сигнала, хотя она и представлена всего одним периодом. На рисунке 7 показан спектр энергии  напомним, что для МНАТ-вейвлета характерный временной масштаб
напомним, что для МНАТ-вейвлета характерный временной масштаб  связан с масштабом вейвлет-преобразования а соотношением
связан с масштабом вейвлет-преобразования а соотношением  Сплошной линией на рисунке показан энергетический спектр сигнала 2, штриховой — сигнала 1. В обоих случаях легко выделяются пики, соответствующие масштабам 5 и 100; мелкомасштабная часть спектра более подробно показана в правом верхнем углу рисунка. С помощью спектров Фурье в обоих случаях удается выявить только высокочастотную составляющую.
Сплошной линией на рисунке показан энергетический спектр сигнала 2, штриховой — сигнала 1. В обоих случаях легко выделяются пики, соответствующие масштабам 5 и 100; мелкомасштабная часть спектра более подробно показана в правом верхнем углу рисунка. С помощью спектров Фурье в обоих случаях удается выявить только высокочастотную составляющую.
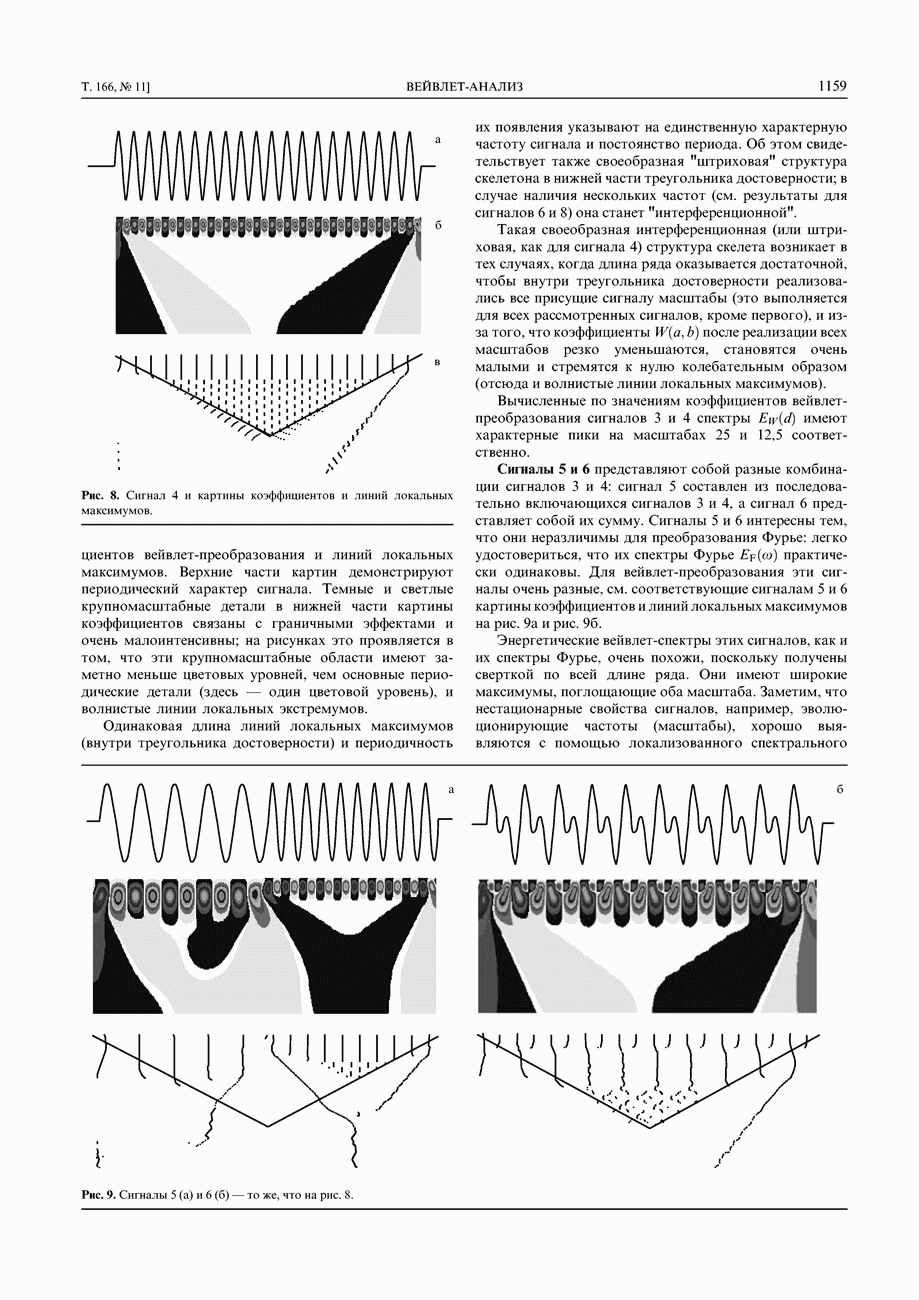
Сигналы 3 и 4 представляют собой синусоиды с периодами равными 50 и 25 соответственно На рисунке 8 показаны сигнал 4 и полученные картины коэффициентов

Рис. 7. Энергетические спектры  сигналов 1 (штриховая линия) и 2 (сплошная линия); в верхнем углу справа более крупно показана мелкомасштабная часть спектра.
сигналов 1 (штриховая линия) и 2 (сплошная линия); в верхнем углу справа более крупно показана мелкомасштабная часть спектра.

Рис. 8. Сигнал 4 и картины коэффициентов и линий локальных максимумов.
вейвлет-преобразования и линий локальных максимумов. Верхние части картин демонстрируют периодический характер сигнала. Темные и светлые крупномасштабные детали в нижней части картины коэффициентов связаны с граничными эффектами и очень малоинтенсивны; на рисунках это проявляется в том, что эти крупномасштабные области имеют заметно меньше цветовых уровней, чем основные периодические детали (здесь — один цветовой уровень), и волнистые линии локальных экстремумов.
Одинаковая длина линий локальных максимумов (внутри треугольника достоверности) и периодичность их появления указывают на единственную характерную частоту сигнала и постоянство периода. Об этом свидетельствует также своеобразная "штриховая" структура скелетона в нижней части треугольника достоверности; в случае наличия нескольких частот (см. результаты для сигналов 6 и 8) она станет "интерференционной".
Такая своеобразная интерференционная (или штриховая, как для сигнала 4) структура скелета возникает в тех случаях, когда длина ряда оказывается достаточной, чтобы внутри треугольника достоверности реализовались все присущие сигналу масштабы (это выполняется для всех рассмотренных сигналов, кроме первого), и из-за того, что коэффициенты  после реализации всех масштабов резко уменьшаются, становятся очень малыми и стремятся к нулю колебательным образом (отсюда и волнистые линии локальных максимумов).
после реализации всех масштабов резко уменьшаются, становятся очень малыми и стремятся к нулю колебательным образом (отсюда и волнистые линии локальных максимумов).
Вычисленные по значениям коэффициентов вейвлет-преобразования сигналов 3 и 4 спектры  имеют характерные пики на масштабах 25 и 12,5 соответственно.
имеют характерные пики на масштабах 25 и 12,5 соответственно.
Сигналы 5 и 6 представляют собой разные комбинации сигналов 3 и 4: сигнал 5 составлен из последовательно включающихся сигналов 3 и 4, а сигнал 6 представляет собой их сумму. Сигналы 5 и 6 интересны тем, что они неразличимы для преобразования Фурье: легко удостовериться, что их спектры Фурье  практически одинаковы. Для вейвлет-преобразования эти сигналы очень разные, см. соответствующие сигналам 5 и 6 картины коэффициентов и линий локальных максимумов на рис. 9а и рис. 96.
практически одинаковы. Для вейвлет-преобразования эти сигналы очень разные, см. соответствующие сигналам 5 и 6 картины коэффициентов и линий локальных максимумов на рис. 9а и рис. 96.
Энергетические вейвлет-спектры этих сигналов, как и их спектры Фурье, очень похожи, поскольку получены сверткой по всей длине ряда. Они имеют широкие максимумы, поглощающие оба масштаба. Заметим, что нестационарные свойства сигналов, например, эволюционирующие частоты (масштабы), хорошо выявляются с помощью локализованного спектрального

Рис. 9. Сигналы 5 (а) и 6 (б) — то же, что на рис. 8.

Рис. 10. Сигналы 7 (а) и 8 (б) - то же, что на рис. 8.
анализа, когда при вычислении спектров  свертка коэффициентов вейвлет-преобразования ведется не по всей длине ряда, а по его отрезкам.
свертка коэффициентов вейвлет-преобразования ведется не по всей длине ряда, а по его отрезкам.
Сигнал 7. На рисунке 10а представлены результаты для сигнала, отличающегося от сигнала 4 лишь фазовым сдвигом на  в середине ряда. Ясно, что спектр Фурье такого сигнала отличается от спектра Фурье сигнала без фазового сдвига наличием дополнительных пиков. Причина в том, что любая деталь сигнала в любой части ряда оказывает влияние на все коэффициенты Фурье и все частоты.
в середине ряда. Ясно, что спектр Фурье такого сигнала отличается от спектра Фурье сигнала без фазового сдвига наличием дополнительных пиков. Причина в том, что любая деталь сигнала в любой части ряда оказывает влияние на все коэффициенты Фурье и все частоты.
Присутствие деталей такого рода в сигнале с учетом прямой связи между частотами в спектре и характерными масштабами процесса может заметно исказить интерпретацию результата. Обычно наличие дополнительных пиков в спектре связывается с наличием нескольких масштабов, которых в приведенном примере на самом деле нет — масштаб один.
Вейвлет-преобразование прекрасно справляется с такого рода особенностью, локализуя ее (см. картины коэффициентов и линий локальных максимумов на рис. 10а).
Сигнал 8. На рисунке 10б приведены результаты для сигнала, представляющего собой сумму двух синусоид с очень близкими частотами; наличие второй частоты проявляется лишь наклоненными линиями локальных максимумов. Подобные наклоны могут появиться и в результате низкочастотной модуляции, однако в таком случае не было бы характерной интерференционной картины скелетона, говорящей о реализации всех масштабов, присутствующих в сигнале.
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
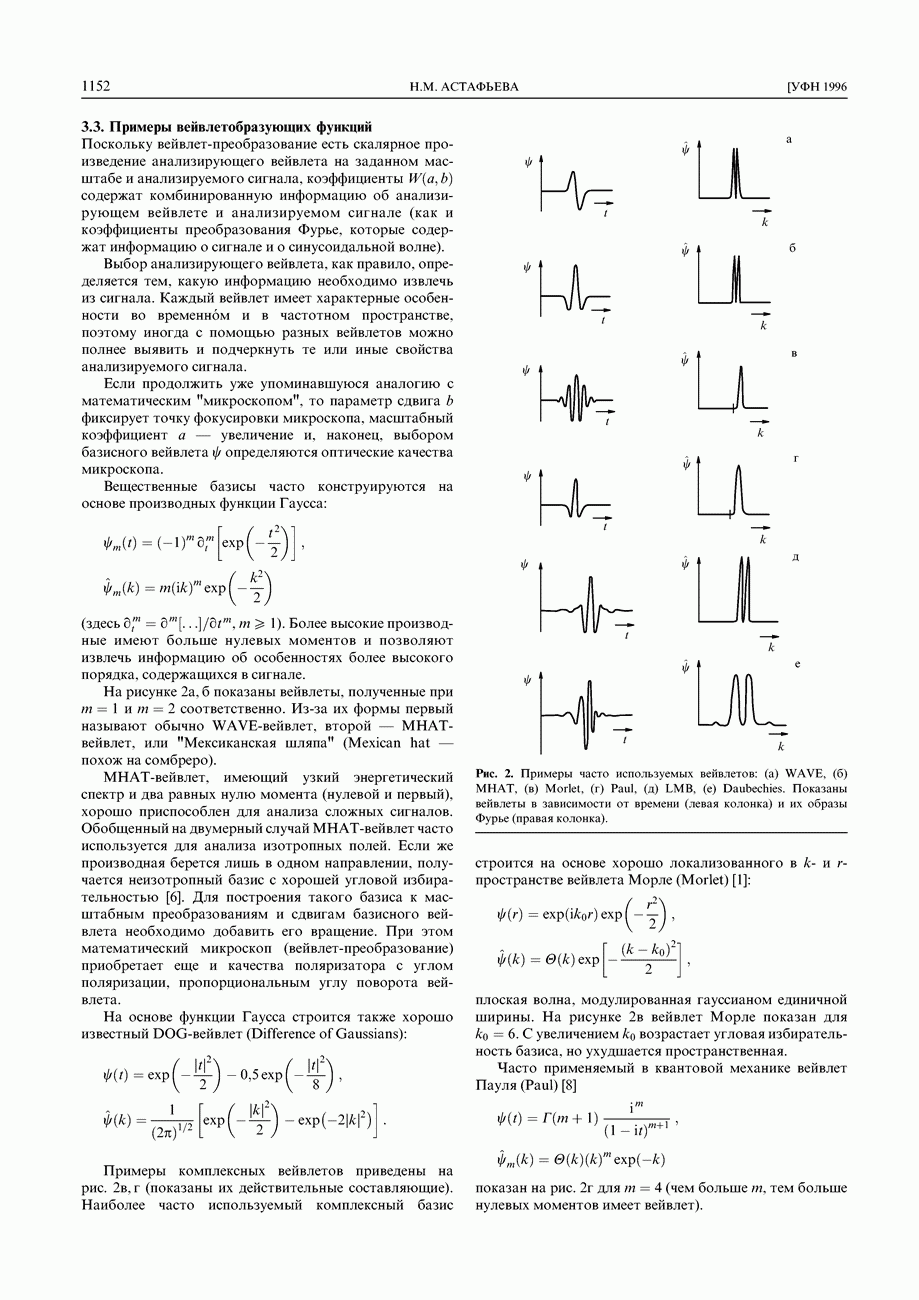
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы