| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. Обратное вейвлет-преобразование
Синусоидальная волна формирует ортонормированный базис функционального пространства  и с обратным преобразованием Фурье проблем не возникает. Ортонормированность же базисов пространства
и с обратным преобразованием Фурье проблем не возникает. Ортонормированность же базисов пространства  построенных на основе вейвлетов, определяется и выбором базисного вейвлета, и способом построения базиса (значениями базисных параметров
построенных на основе вейвлетов, определяется и выбором базисного вейвлета, и способом построения базиса (значениями базисных параметров 
Конечно же, вейвлет может считаться базисной функцией  только в том случае, если построенный с его помощью базис ортонормирован и обратное преобразование существует. Однако строгие доказательства полноты и ортогональности сложны и громоздки, примеры этого можно видеть в [2-5], где разрабатывается теория вейвлет-преобразования. Кроме того, для практических целей часто достаточно бывает устойчивости и "приблизительной" ортогональности системы функций разложения, т.е. достаточно, чтобы она была "почти базисом". Как правило, для анализа сигналов используются такие "почти базисные" вейвлеты.
только в том случае, если построенный с его помощью базис ортонормирован и обратное преобразование существует. Однако строгие доказательства полноты и ортогональности сложны и громоздки, примеры этого можно видеть в [2-5], где разрабатывается теория вейвлет-преобразования. Кроме того, для практических целей часто достаточно бывает устойчивости и "приблизительной" ортогональности системы функций разложения, т.е. достаточно, чтобы она была "почти базисом". Как правило, для анализа сигналов используются такие "почти базисные" вейвлеты.
За подробным изложением и доказательствами отошлем к уже цитированным работам, здесь же выпишем обратное преобразование лишь для тех двух случаев, что описаны выше: для базиса (7), допускающего расширения и сдвиги  и базиса (10), построенного при произвольных значениях
и базиса (10), построенного при произвольных значениях 
При базисных параметрах  обратное вейвлет-преобразование записывается с помощью того же базиса (10), что и прямое:
обратное вейвлет-преобразование записывается с помощью того же базиса (10), что и прямое:

 — нормализующий коэффициент (аналогичный коэффициенту
— нормализующий коэффициент (аналогичный коэффициенту  нормализующему преобразование Фурье):
нормализующему преобразование Фурье):

(крышечкой сверху обозначается фурье-образ).
Условие конечности константы  ограничивает класс функций
ограничивает класс функций  которые могут быть использованы в качестве базисных вейвлетов. В частности, очевидно, что образ Фурье
которые могут быть использованы в качестве базисных вейвлетов. В частности, очевидно, что образ Фурье  должен быть равен нулю в начале координат
должен быть равен нулю в начале координат  , следовательно, должен быть равен нулю по крайней мере нулевой момент:
, следовательно, должен быть равен нулю по крайней мере нулевой момент:

Чаще всего в приложениях достаточно рассмотрения только положительных частот, т.е.  вейвлет, соответственно, должен удовлетворять условию
вейвлет, соответственно, должен удовлетворять условию

В случае дискретного вейвлет-преобразования устойчивый базис определяется следующим образом.
Функция  называется
называется  -функцией, если базис
-функцией, если базис  определенный выражением (7), является базисом Рисса (Riesz) в том смысле, что существуют две константы А и
определенный выражением (7), является базисом Рисса (Riesz) в том смысле, что существуют две константы А и  для которых соотношение
для которых соотношение

выполняется при любой (ограниченной, дважды квадратично суммируемой) последовательности  :
:

Для любой  -функции существует базис
-функции существует базис  — "двойник" базиса
— "двойник" базиса  (в том смысле, что
(в том смысле, что  с помощью которого можно построить рекон-струкционную формулу
с помощью которого можно построить рекон-струкционную формулу

Если  — ортогональный вейвлет и
— ортогональный вейвлет и  — ортонормированный базис, то
— ортонормированный базис, то  совпадают и формула (14) является формулой обратного преобразования. Если
совпадают и формула (14) является формулой обратного преобразования. Если  — не ортогональный вейвлет, но является двухместным или парным
— не ортогональный вейвлет, но является двухместным или парным  -вейвлетом (dyadic wavelet), то он имеет двойника
-вейвлетом (dyadic wavelet), то он имеет двойника  с помощью которого двойник семейства
с помощью которого двойник семейства  строится подобно базису (7):
строится подобно базису (7):

В общем же случае реконструкционная формула (14) даже не обязательно является вейвлет-рядом в том смысле, что  не является вейвлетом и
не является вейвлетом и  может не иметь базиса-двойника, построенного по типу (10).
может не иметь базиса-двойника, построенного по типу (10).
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
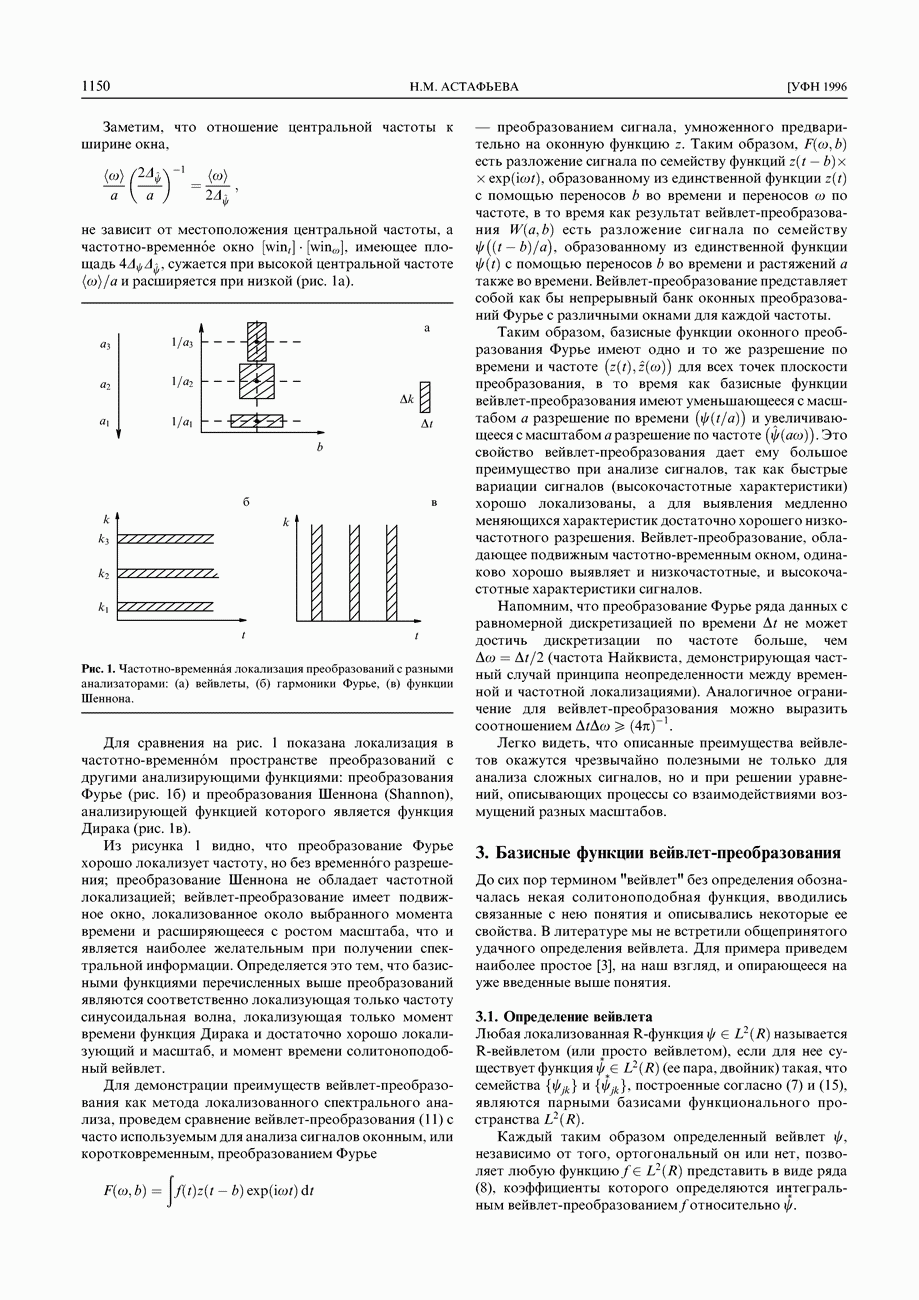
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
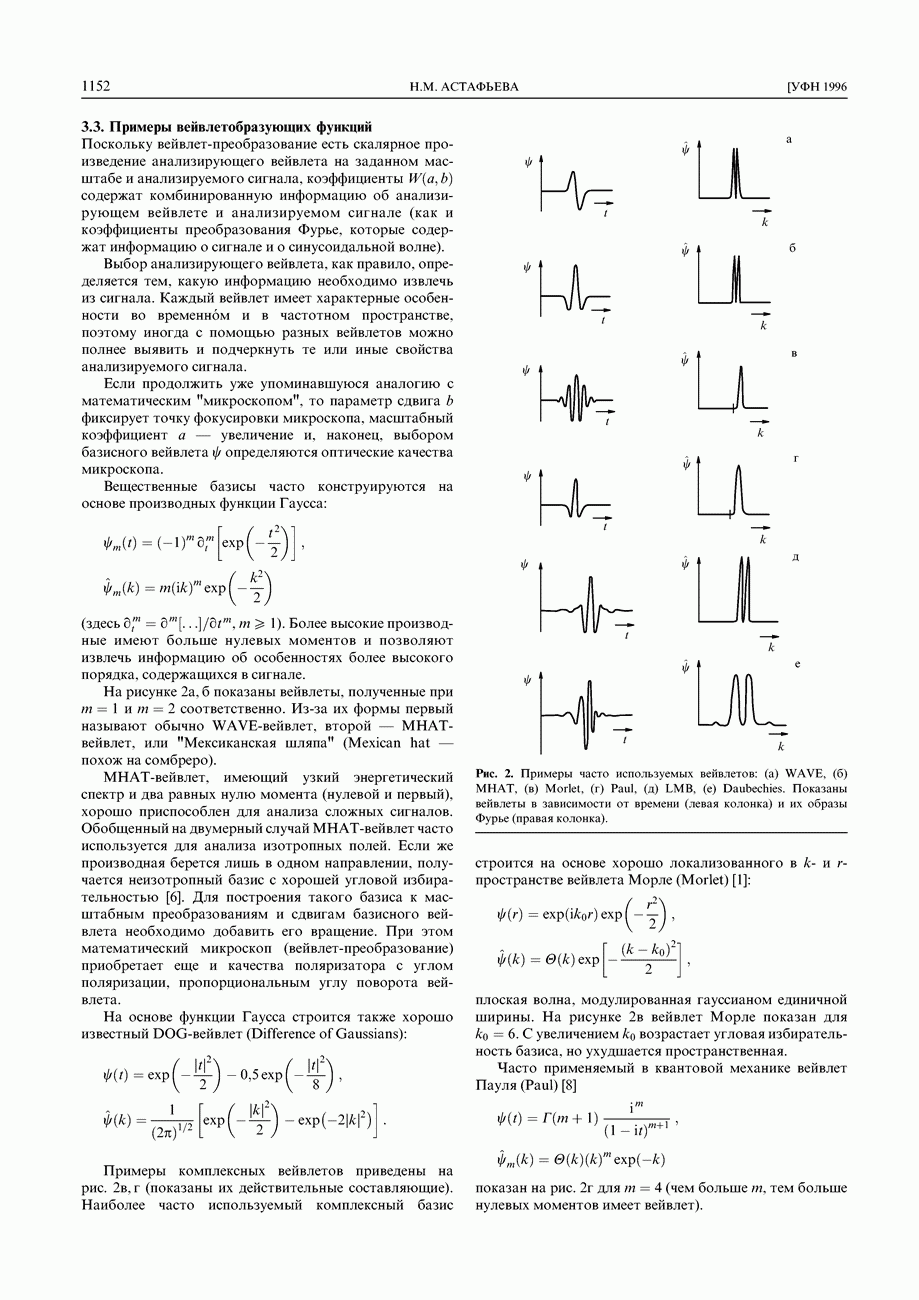
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
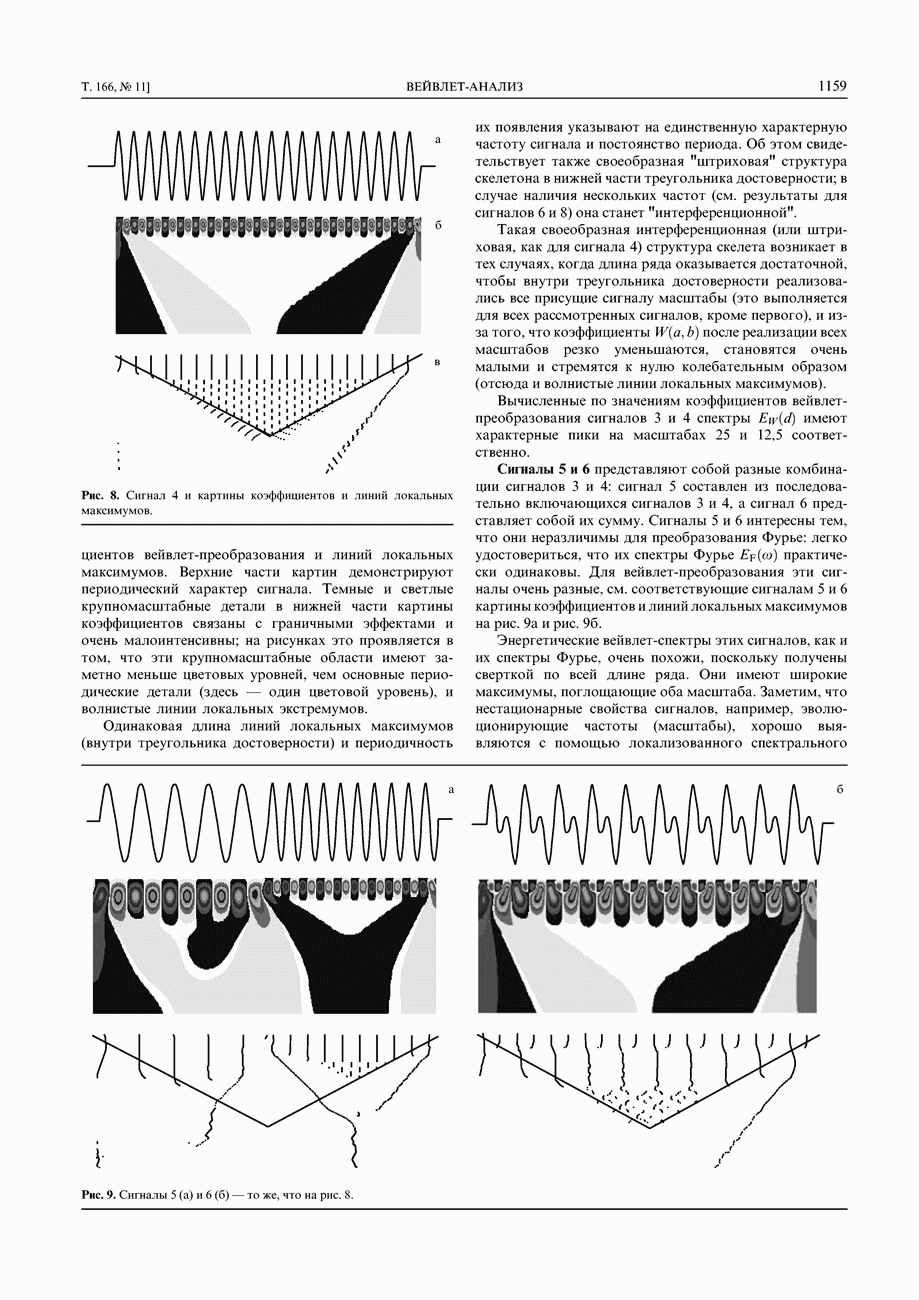
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы