| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. Некоторые возможности вейвлет-анализа
Имея вейвлет-спектры, можно вычислить полезные характеристики изучаемого процесса и проанализировать многие его свойства. Опишем более подробно возможности анализа особенностей сигнала и его энергетических характеристик.
4.3.1. Анализ локальной регулярности [6,13].
Рассмотрим некоторые следствия свойства масштабной инвариантности (24).
Если  , т.е. анализируемая функция в точке
, т.е. анализируемая функция в точке  непрерывно дифференцируема вплоть до производной порядка
непрерывно дифференцируема вплоть до производной порядка  то коэффициенты ее вейвлет-преобразования при
то коэффициенты ее вейвлет-преобразования при  должны подчиняться неравенству
должны подчиняться неравенству

Если  т.е. анализируемая функция принадлежит пространству холдеровских функций с показателем
т.е. анализируемая функция принадлежит пространству холдеровских функций с показателем  (напомним, что это означает:
(напомним, что это означает:  непрерывна, не обязательно дифференцируема в
непрерывна, не обязательно дифференцируема в  но такая, что
но такая, что  то коэффициенты ее вейвлет-преобразования при
то коэффициенты ее вейвлет-преобразования при  должны подчиняться соотношению
должны подчиняться соотношению

Вейвлет-преобразование так устроено, что  — регулярная функция даже при нерегулярной
— регулярная функция даже при нерегулярной  Вся информация о возможной особенности
Вся информация о возможной особенности  (локализация
(локализация  , интенсивность с, показатель а) заключена в асимптотическом поведении коэффициентов
, интенсивность с, показатель а) заключена в асимптотическом поведении коэффициентов  при малых а. Если коэффициенты на малых масштабах расходятся, то
при малых а. Если коэффициенты на малых масштабах расходятся, то  имеет особенность в
имеет особенность в  и показатель сингулярности а определяется наклоном зависимости
и показатель сингулярности а определяется наклоном зависимости  а. Если они, напротив, близки к нулю в окрестности
а. Если они, напротив, близки к нулю в окрестности  на малых масштабах, то
на малых масштабах, то  в точке
в точке  регулярна.
регулярна.
Описанное свойство часто и с успехом используется при анализе фрактальных и мультифрактальных сигналов [14, 15]. Типичным свойством фрактальных множеств является их асимптотическое самоподобие. Так, разглядывая/вблизи точки  с разным увеличением, мы на разных масштабах увидим практически ее же:
с разным увеличением, мы на разных масштабах увидим практически ее же:

Базис преобразования самоподобен; легко показать, что и коэффициенты преобразования масштабируются с тем же показателем, что и анализируемая функция:

Отсюда легко получить скейлинговый показатель  который, как известно, тесно связан с фрактальной размерностью множества. Анализ мультифрактального множества позволяет определить спектр показателей и спектр размерностей.
который, как известно, тесно связан с фрактальной размерностью множества. Анализ мультифрактального множества позволяет определить спектр показателей и спектр размерностей.
Особо отметим, что анализ локальной регулярности в некотором смысле универсален — он не зависит от выбора анализирующего вейвлета.
4.3.2. Энергетические характеристики [6,16].
Рассмотрим некоторые следствия равенства (26). Из существования для вейвлет-преобразования аналога равенства Парсеваля следует, что в пространстве действительных функций полная энергия сигнала  может быть записана через амплитуды вейвлет-преобразования в виде
может быть записана через амплитуды вейвлет-преобразования в виде

Плотность энергии сигнала  характеризует энергетические уровни (уровни возбуждения) исследуемого сигнала
характеризует энергетические уровни (уровни возбуждения) исследуемого сигнала  в пространстве
в пространстве  (масштаб, время).
(масштаб, время).
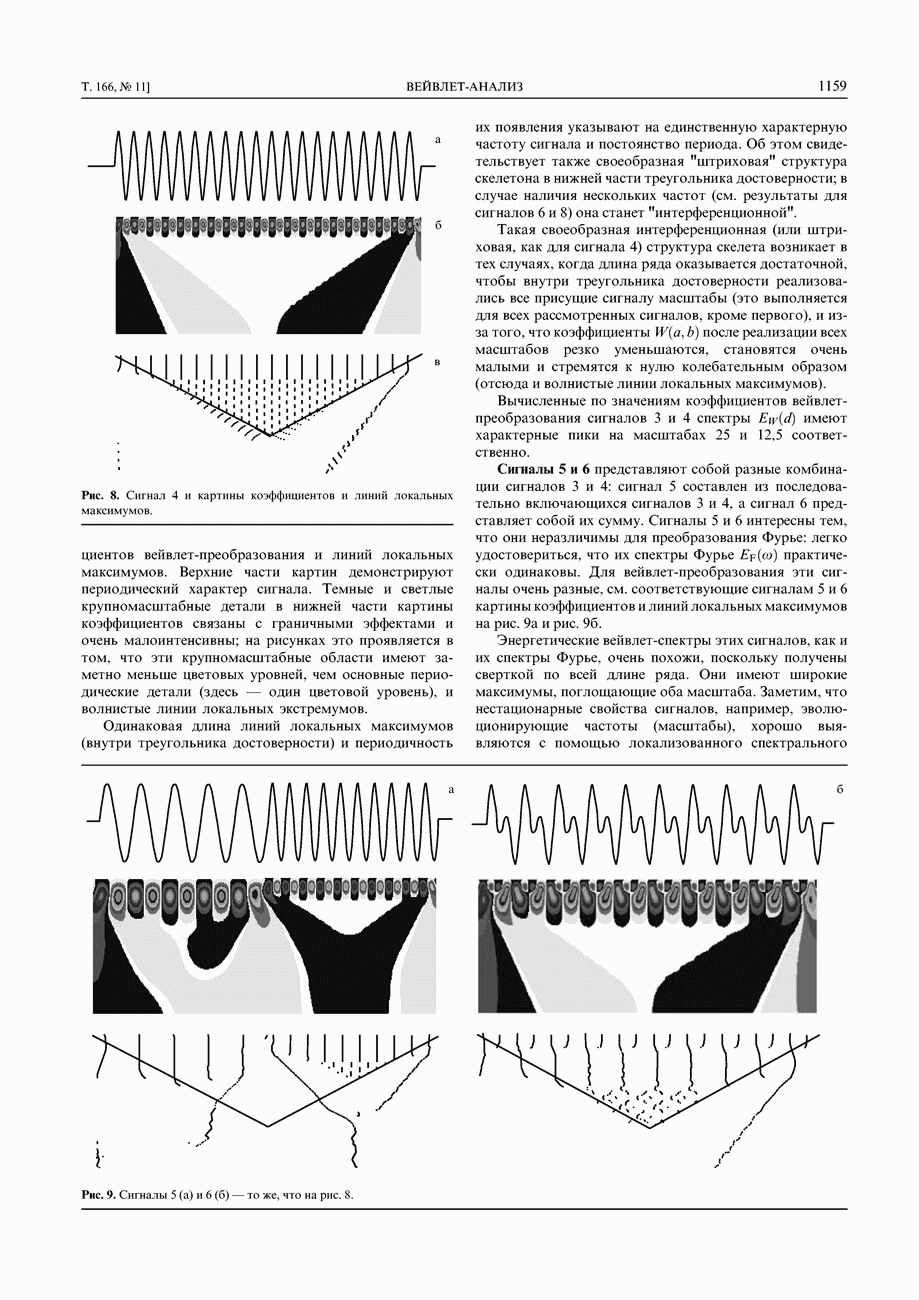
На рисунке  представлена картина распределения плотности энергии, полученная для части ряда потока ионов солнечного ветра. На картине наиболее светлые места соответствуют наибольшим значениям
представлена картина распределения плотности энергии, полученная для части ряда потока ионов солнечного ветра. На картине наиболее светлые места соответствуют наибольшим значениям  сгущение цвета до черного соответствует уменьшению
сгущение цвета до черного соответствует уменьшению  до нуля. Чтобы лучше были видны детали, распределение плотности энергии показано для части ряда и для верхней трети диапазона масштабов (соответствующий фрагмент выделен рамкой на рис. 3в).
до нуля. Чтобы лучше были видны детали, распределение плотности энергии показано для части ряда и для верхней трети диапазона масштабов (соответствующий фрагмент выделен рамкой на рис. 3в).
Показанный фрагмент демонстрирует, что энергия неравномерно распределена по масштабам — есть выделенные масштабы. Обе картины демонстрируют нестационарную структуру анализируемого процесса с элементами квазипериодичности, с эволюционирующими частотами и с диапазонами локальных периодичностей на разных масштабах.
Локальный спектр энергии. Одной из основных особенностей вейвлет-преобразования является возможность получать локализованные характеристики и изучать локальные свойства процессов. Как ни парадоксально звучат слова "локальный энергетический спектр", однако природа вейвлет-преобразования такова, что термин имеет право на существование. Поясним сказанное.
Зная плотность энергии  можно с помощью окна определить локальную плотность энергии в точке
можно с помощью окна определить локальную плотность энергии в точке  :
:

Оконная функция  "поддерживает" диапазон около
"поддерживает" диапазон около  и удовлетворяет равенству
и удовлетворяет равенству

Если в качестве  выбрать функцию Дирака, то локальный спектр энергии примет вид
выбрать функцию Дирака, то локальный спектр энергии примет вид

Эта характеристика позволяет проанализировать временную динамику передачи энергии процесса по масштабам — обмен энергией между составляющими процесс компонентами разного масштаба в любой заданный момент времени.
Глобальный спектр энергии. Полная энергия распределена по масштабам в соответствии с глобальным спектром энергии коэффициентов вейвлет-преобразования

Его называют также скалограммой (scalogram) или дисперсией вейвлет-преобразования (wavelet variance).
На рисунке 5а представлены спектр мощности  потока ионов солнечного ветра (рис. 3а) и скалограмма
потока ионов солнечного ветра (рис. 3а) и скалограмма  — глобальный спектр энергии коэффициентов вейвлет-преобразования того же сигнала. Спектры достаточно хорошо согласуются, но спектр, вычисленный по коэффициентам вейвлет-преобразования, — гораздо более гладкая кривая. Причина заключается в том, что вейвлет-спектр энергии сигнала
— глобальный спектр энергии коэффициентов вейвлет-преобразования того же сигнала. Спектры достаточно хорошо согласуются, но спектр, вычисленный по коэффициентам вейвлет-преобразования, — гораздо более гладкая кривая. Причина заключается в том, что вейвлет-спектр энергии сигнала  соответствует сглаженному спектру мощности
соответствует сглаженному спектру мощности  . Это можно показать, выразив спектр энергии
. Это можно показать, выразив спектр энергии  через спектр энергии сигнала в пространстве Фурье
через спектр энергии сигнала в пространстве Фурье 

Легко видеть, что скалограмма  соответствует спектру мощности
соответствует спектру мощности  сглаженному на каждом масштабе спектром Фурье анализирующего вейвлета.
сглаженному на каждом масштабе спектром Фурье анализирующего вейвлета.

Рис. 5. Энергетические спектры потока ионов солнечного ветра: (а) спектр мощности  и скалограмма
и скалограмма  в зависимости от частоты,
в зависимости от частоты,  скалограммы для четырех временных диапазонов (в рамке) и полная в зависимости от масштаба (он растет вверх). Графики даны в двойном логарифмическом масштабе.
скалограммы для четырех временных диапазонов (в рамке) и полная в зависимости от масштаба (он растет вверх). Графики даны в двойном логарифмическом масштабе.
Вейвлет-преобразование, предоставляющее нам как бы временную развертку спектра, позволяет получить и более локализованную энергетическую информацию. На рисунке 5б представлены четыре скалограммы  полученные сверткой не по всей длине ряда (рис. 3а), а отдельно для каждой четвертой его части. На том же рисунке для сравнения приведен глобальный спектр (на рис. 5а он показан в зависимости от частоты, на рис. 5б скалограммы показаны в зависимости от масштаба, который здесь растет вверх). Скалограммы, полученные по диапазонам, позволяют проследить эволюцию распределения энергии по масштабам.
полученные сверткой не по всей длине ряда (рис. 3а), а отдельно для каждой четвертой его части. На том же рисунке для сравнения приведен глобальный спектр (на рис. 5а он показан в зависимости от частоты, на рис. 5б скалограммы показаны в зависимости от масштаба, который здесь растет вверх). Скалограммы, полученные по диапазонам, позволяют проследить эволюцию распределения энергии по масштабам.
Энергия сигнала определяется через спектр энергии равенством

Таким образом, величина  пропорциональна площади под кривой
пропорциональна площади под кривой  , а скалограмма отражает относительный вклад различных масштабов в полную энергию и выявляет распределение энергии процесса по масштабам.
, а скалограмма отражает относительный вклад различных масштабов в полную энергию и выявляет распределение энергии процесса по масштабам.
Анализируемая функция имеет конечную энергию, а анализирующий вейвлет — нулевое среднее значение, вследствие чего спектр энергии  должен стремиться к нулю на обоих концах шкалы масштабов и должен иметь по крайней мере один максимум. Положение подобных максимумов (пиков) спектра Фурье
должен стремиться к нулю на обоих концах шкалы масштабов и должен иметь по крайней мере один максимум. Положение подобных максимумов (пиков) спектра Фурье  привычно связывается с частотами и соответствующими характерными модами анализируемого сигнала, несущими в себе основную энергию процесса. Максимумы энергетического спектра
привычно связывается с частотами и соответствующими характерными модами анализируемого сигнала, несущими в себе основную энергию процесса. Максимумы энергетического спектра  интерпретируются аналогично — они определяют масштабы процесса, вносящие основной вклад в полную энергию
интерпретируются аналогично — они определяют масштабы процесса, вносящие основной вклад в полную энергию  .
.
Покажем на простом примере связь между выявленным в результате вейвлет-преобразования масштабом и характерным масштабом, полученным из спектра Фурье. Пусть

- синусоида; ее вейвлет-преобразование, записанное через образы Фурье (см., например, формулу (17)), есть

а спектр —  Необходимыми достаточным условием наличия пика на масштабе
Необходимыми достаточным условием наличия пика на масштабе  является равенство нулю производной
является равенство нулю производной  при
при  Условие выполняется при
Условие выполняется при  , где
, где  — зависящая от вейвлета
— зависящая от вейвлета  константа с размерностью частоты. Для многих вейвлетов константа
константа с размерностью частоты. Для многих вейвлетов константа  вычисляется аналитически; так, для HAAR- и МНАТ-вейвлетов она равна
вычисляется аналитически; так, для HAAR- и МНАТ-вейвлетов она равна  соответственно.
соответственно.
На практике, если скалограмма  имеет пик при
имеет пик при  характерный временной масштаб определяется как
характерный временной масштаб определяется как  Множитель 1/2 появился из-за того, что определяется не период, а масштаб элементарного события, детали. В этом смысле синус, например, имеет две элементарные детали на периоде.
Множитель 1/2 появился из-за того, что определяется не период, а масштаб элементарного события, детали. В этом смысле синус, например, имеет две элементарные детали на периоде.
Константа  получена для простой функции. Распространяя результат на произвольный сигнал, даже негармонический, мы предполагаем, что положение максимума спектра
получена для простой функции. Распространяя результат на произвольный сигнал, даже негармонический, мы предполагаем, что положение максимума спектра  (т.е. выявленный масштаб) можно интерпретировать как среднюю продолжительность элементарного события (событий), вносящего основной вклад в энергию анализируемого процесса. Этот факт проверен на многих известных сигналах с разными вейвлетами и признан очень хорошим приближением (см., например, [16]).
(т.е. выявленный масштаб) можно интерпретировать как среднюю продолжительность элементарного события (событий), вносящего основной вклад в энергию анализируемого процесса. Этот факт проверен на многих известных сигналах с разными вейвлетами и признан очень хорошим приближением (см., например, [16]).
Выпишем еще две характеристики, определяемые через плотность энергии, — меру локальной перемежаемости и меру контрастности анализируемого сигнала.
Мера локальной перемежаемости:

— мера локальных отклонений от среднего поля спектров на каждом масштабе; она позволяет определить степень неравномерности распределения энергии по масштабам (угловыми скобками здесь обозначено усреднение).
Равенство  при всех а и
при всех а и  означает, что энергия распределена равномерно и все локальные спектры энергии одинаковы;
означает, что энергия распределена равномерно и все локальные спектры энергии одинаковы;  означает, что вклад компоненты масштаба а в точке
означает, что вклад компоненты масштаба а в точке  раз превосходит усредненный по всем
раз превосходит усредненный по всем 
Мера контрастности

позволяет определять даже малые изменения в сигнале, когда необходимо, например, выявить структурированность слабого сигнала или слабые вариации на фоне крупной структуры (встроенные структуры).
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
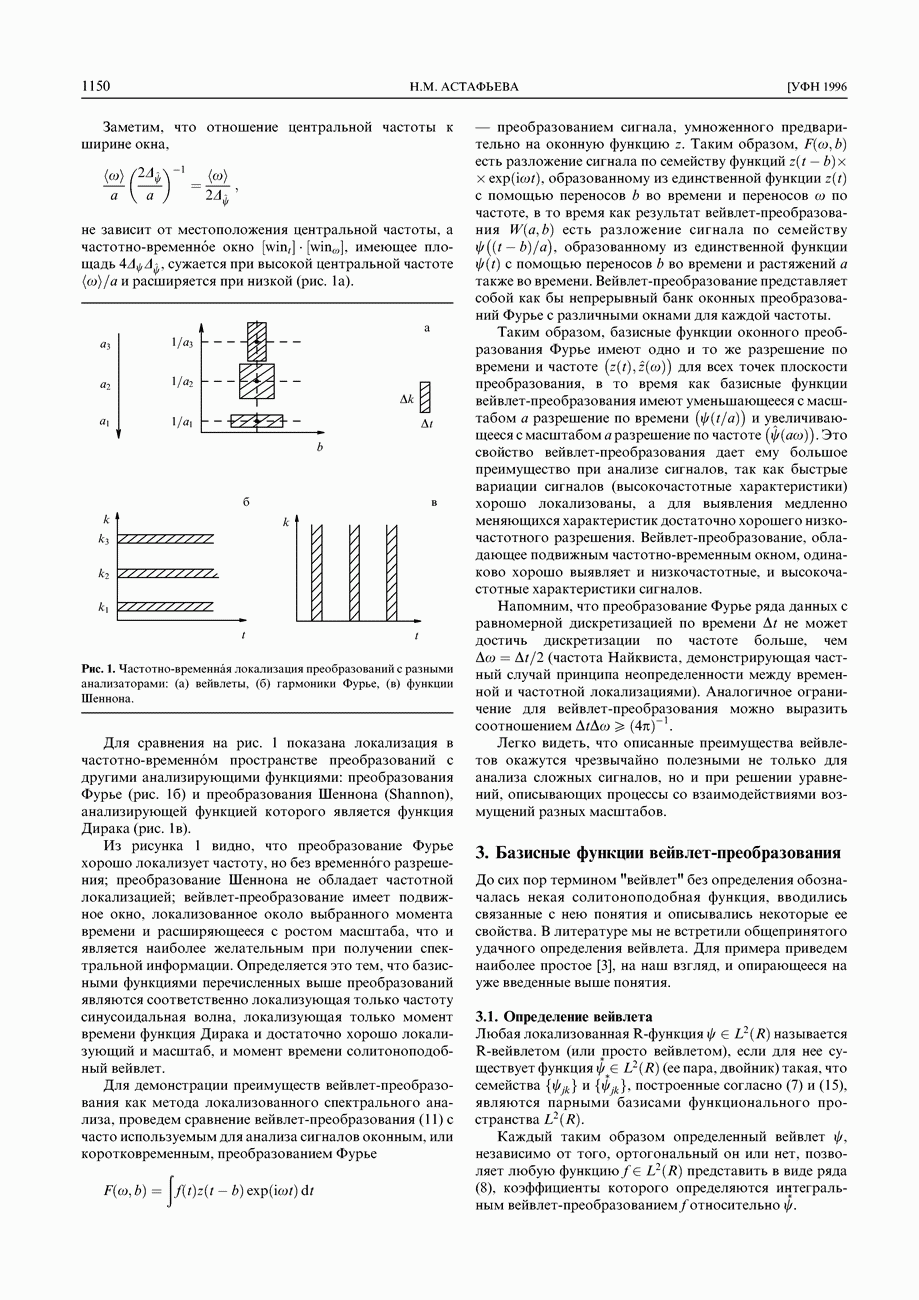
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
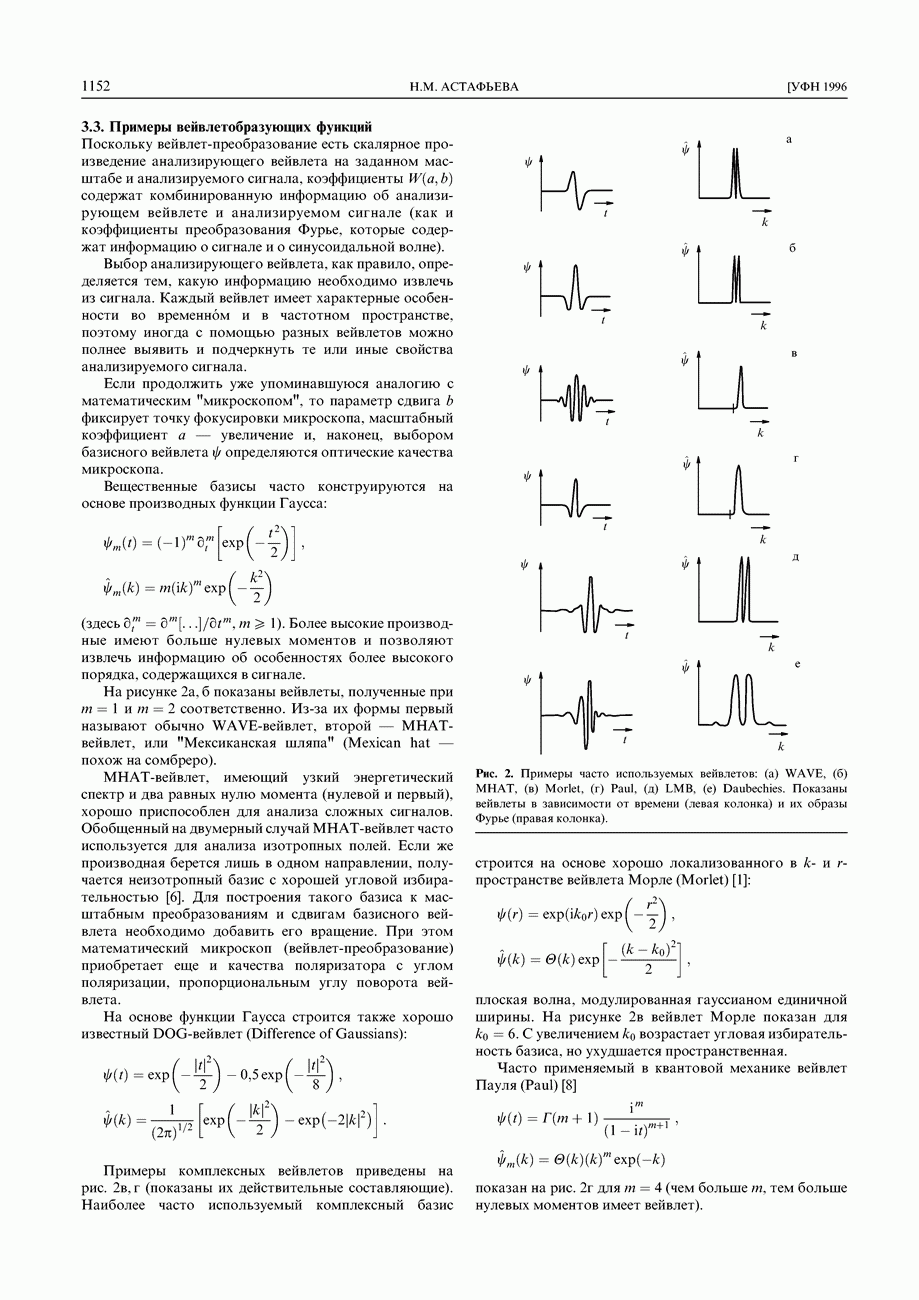
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы