| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Частотно-временная локализация
Преобразование Фурье и ряды Фурье являются прекрасным математическим аппаратом для физической интерпретации процессов при анализе характеризующих их сигналов. Однако иногда они оказываются недостаточно эффективными.
Реальный сигнал всегда (или, как правило) принадлежит пространству  Преобразование Фурье сигнала
Преобразование Фурье сигнала  с конечной энергией, определенной нормой
с конечной энергией, определенной нормой  представляет собой спектр этого сигнала:
представляет собой спектр этого сигнала:

В некоторых случаях физическая интерпретация с помощью этой формулы бывает затруднительна. Так, чтобы получить спектральную информацию на выбранной частоте, необходимо иметь и прошлую, и будущую временную информацию; к тому же формула не учитывает, что частота может эволюционировать со временем. Преобразование Фурье, например, не отличает сигнал, представляющий собой сумму двух синусоид с разными частотами, от сигнала, состоящего из тех же синусоид, включающихся последовательно одна за другой (пример рассмотрен в разделе 5).
Кроме того, известно, что частота сигнала обратно пропорциональна его продолжительности. Поэтому для получения высокочастотной информации с хорошей точностью важно извлекать ее из относительно малых временных интервалов, а не из всего сигнала; и наоборот — низкочастотную спектральную информацию извлекать из относительно широких временных интервалов сигнала.
Часть описанных трудностей снимается при использовании оконного преобразования Фурье. Однако бесконечно осциллирующая базисная функция (синусоидальная волна) не позволяет получать по-настоящему локализованную информацию. Элементом базиса вейв-лет-преобразования является хорошо локализованная функция, быстро стремящаяся к нулю вне небольшого интервала, что позволяет провести "локализованный спектральный анализ" — смысл этого несколько странного сочетания слов станет ясен из дальнейшего. Иными словами, вейвлет-преобразование автоматически обладает подвижным частотно-временным окном, узким на малых масштабах и широким на больших.
Каковы же параметры частотно-временного окна вейвлет-преобразования? Поскольку и сам вейвлет  и его фурье-образ
и его фурье-образ  достаточно быстро спадают, они могут быть использованы как "оконные функции" с "центром" и "шириной", определяемыми следующим образом.
достаточно быстро спадают, они могут быть использованы как "оконные функции" с "центром" и "шириной", определяемыми следующим образом.
Для нетривиальной оконной функции  (необходимо, чтобы функция
(необходимо, чтобы функция  также принадлежала
также принадлежала  ее центр
ее центр  и радиус
и радиус  определяются формулами
определяются формулами

при этом ширина оконной функции есть 
Пусть  — определенные по этим формулам центры и радиусы вейвлета
— определенные по этим формулам центры и радиусы вейвлета  и его фурье-образа
и его фурье-образа  соответственно. Тогда интегральное вейвлет-преобразование (11) ограничено "временным окном"
соответственно. Тогда интегральное вейвлет-преобразование (11) ограничено "временным окном"

т.е. имеет место временная локализация с центром окна в  и шириной окна
и шириной окна 
Введем функцию  которая также является оконной функцией с центром в нуле и радиусом А. Воспользовавшись равенством
которая также является оконной функцией с центром в нуле и радиусом А. Воспользовавшись равенством  можно записать интегральное вейвлет-преобразование (11) для фурье-образа в виде
можно записать интегральное вейвлет-преобразование (11) для фурье-образа в виде

Если отвлечься от фазового сдвига, то станет очевидным, что преобразование (17) дает и о спектре  сигнала
сигнала  локализованную информацию с "частотным окном"
локализованную информацию с "частотным окном"

Частотная локализация происходит около центра окна в  шириной окна, равной
шириной окна, равной  .
.
Заметим, что отношение центральной частоты к ширине окна,

не зависит от местоположения центральной частоты, а частотно-временное окно  имеющее площадь
имеющее площадь  сужается при высокой центральной частоте
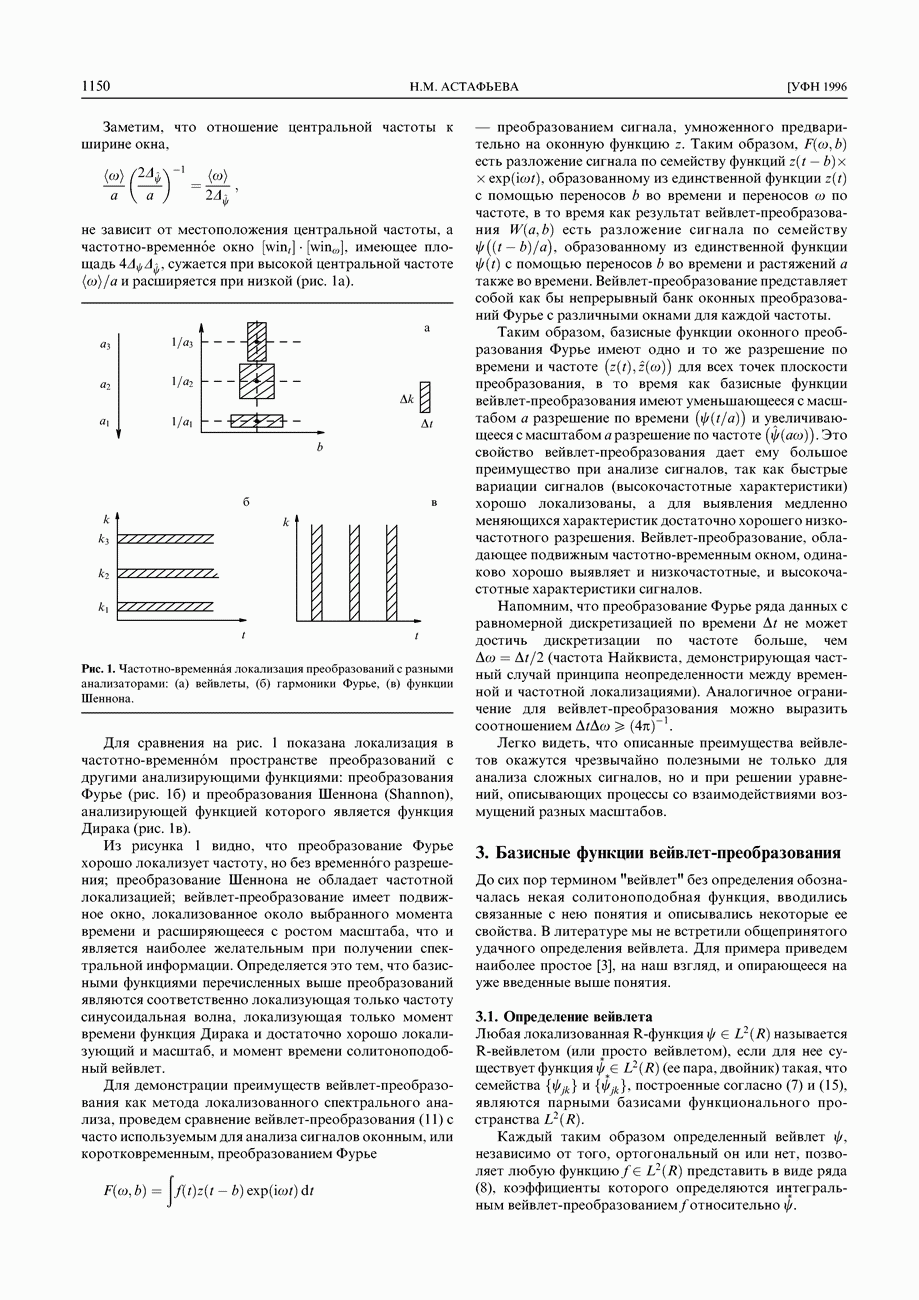
сужается при высокой центральной частоте  и расширяется при низкой (рис. 1а).
и расширяется при низкой (рис. 1а).

Рис. 1. Частотно-временная локализация преобразований с разными анализаторами: (а) вейвлеты,  гармоники Фурье, (в) функции Шеннона.
гармоники Фурье, (в) функции Шеннона.
Для сравнения на рис. 1 показана локализация в частотно-временном пространстве преобразований с другими анализирующими функциями: преобразования Фурье (рис. 16) и преобразования Шеннона (Shannon), анализирующей функцией которого является функция Дирака (рис. 1в).
Из рисунка 1 видно, что преобразование Фурье хорошо локализует частоту, но без временного разрешения; преобразование Шеннона не обладает частотной локализацией; вейвлет-преобразование имеет подвижное окно, локализованное около выбранного момента времени и расширяющееся с ростом масштаба, что и является наиболее желательным при получении спектральной информации. Определяется это тем, что базисными функциями перечисленных выше преобразований являются соответственно локализующая только частоту синусоидальная волна, локализующая только момент времени функция Дирака и достаточно хорошо локализующий и масштаб, и момент времени солитоноподобный вейвлет.
Для демонстрации преимуществ вейвлет-преобразования как метода локализованного спектрального анализа, проведем сравнение вейвлет-преобразования (11) с часто используемым для анализа сигналов оконным, или коротковременным, преобразованием Фурье

— преобразованием сигнала, умноженного предварительно на оконную функцию  Таким образом,
Таким образом,  есть разложение сигнала по семейству функций
есть разложение сигнала по семейству функций  образованному из единственной функции
образованному из единственной функции  с помощью переносов
с помощью переносов  во времени и переносов
во времени и переносов  по частоте, в то время как результат вейвлет-преобразования
по частоте, в то время как результат вейвлет-преобразования  есть разложение сигнала по семейству
есть разложение сигнала по семейству  образованному из единственной функции
образованному из единственной функции  с помощью переносов
с помощью переносов  во времени и растяжений а также во времени. Вейвлет-преобразование представляет собой как бы непрерывный банк оконных преобразований Фурье с различными окнами для каждой частоты.
во времени и растяжений а также во времени. Вейвлет-преобразование представляет собой как бы непрерывный банк оконных преобразований Фурье с различными окнами для каждой частоты.
Таким образом, базисные функции оконного преобразования Фурье имеют одно и то же разрешение по времени и частоте  для всех точек плоскости преобразования, в то время как базисные функции вейвлет-преобразования имеют уменьшающееся с масштабом а разрешение по времени
для всех точек плоскости преобразования, в то время как базисные функции вейвлет-преобразования имеют уменьшающееся с масштабом а разрешение по времени  и увеличивающееся с масштабом а разрешение по частоте
и увеличивающееся с масштабом а разрешение по частоте  Это свойство вейвлет-преобразования дает ему большое преимущество при анализе сигналов, так как быстрые вариации сигналов (высокочастотные характеристики) хорошо локализованы, а для выявления медленно меняющихся характеристик достаточно хорошего низкочастотного разрешения. Вейвлет-преобразование, обладающее подвижным частотно-временным окном, одинаково хорошо выявляет и низкочастотные, и высокочастотные характеристики сигналов.
Это свойство вейвлет-преобразования дает ему большое преимущество при анализе сигналов, так как быстрые вариации сигналов (высокочастотные характеристики) хорошо локализованы, а для выявления медленно меняющихся характеристик достаточно хорошего низкочастотного разрешения. Вейвлет-преобразование, обладающее подвижным частотно-временным окном, одинаково хорошо выявляет и низкочастотные, и высокочастотные характеристики сигналов.
Напомним, что преобразование Фурье ряда данных с равномерной дискретизацией по времени  не может достичь дискретизации по частоте больше, чем
не может достичь дискретизации по частоте больше, чем  (частота Найквиста, демонстрирующая частный случай принципа неопределенности между временной и частотной локализациями). Аналогичное ограничение для вейвлет-преобразования можно выразить соотношением
(частота Найквиста, демонстрирующая частный случай принципа неопределенности между временной и частотной локализациями). Аналогичное ограничение для вейвлет-преобразования можно выразить соотношением 
Легко видеть, что описанные преимущества вейвлетов окажутся чрезвычайно полезными не только для анализа сложных сигналов, но и при решении уравнений, описывающих процессы со взаимодействиями возмущений разных масштабов.
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
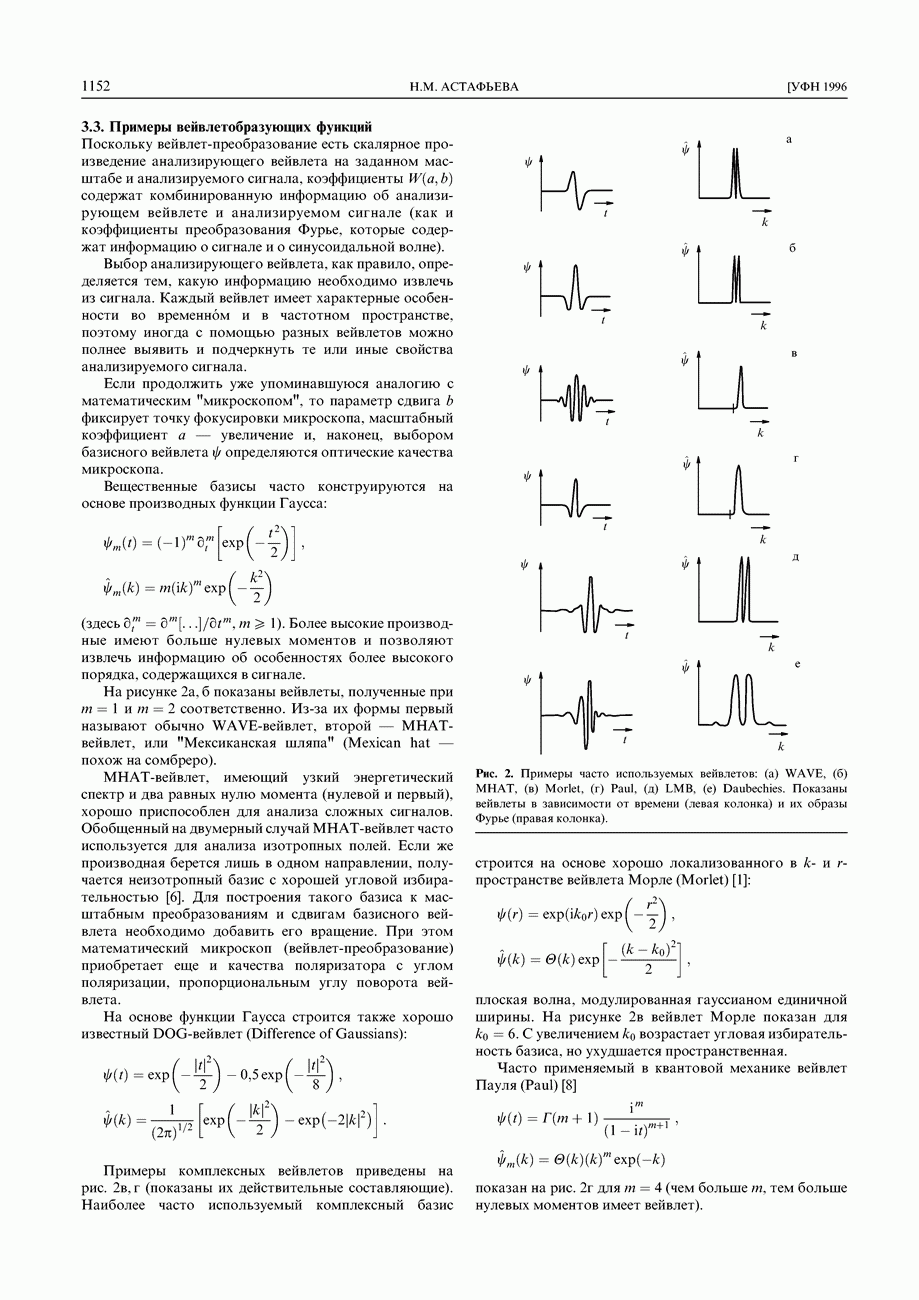
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
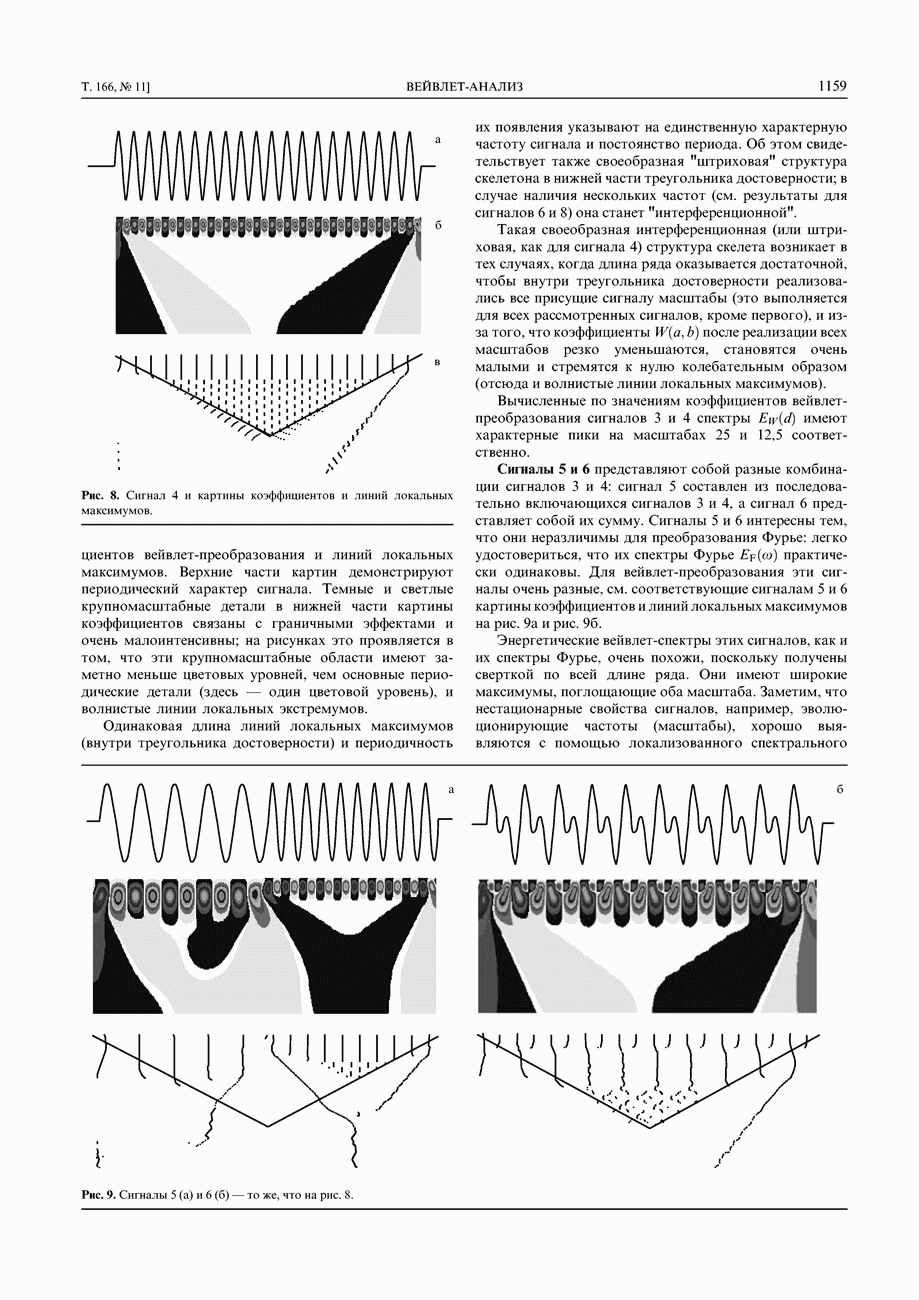
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы