| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Разложение по вейвлетам
Рассмотрим пространство  функций
функций  определенных на всей действительной оси
определенных на всей действительной оси  и обладающих конечной энергией (нормой)
и обладающих конечной энергией (нормой)

Функциональные пространства  существенно различны. В частности, локальное среднее значение каждой функции из
существенно различны. В частности, локальное среднее значение каждой функции из  должно стремиться к нулю на
должно стремиться к нулю на  Синусоидальная волна не принадлежит
Синусоидальная волна не принадлежит  , следовательно, семейство синусоидальных волн
, следовательно, семейство синусоидальных волн  не может быть базисом функционального пространства
не может быть базисом функционального пространства  Попробуем найти достаточно простые функции для конструирования базиса пространства
Попробуем найти достаточно простые функции для конструирования базиса пространства  .
.
"Волны", образующие пространство  должны стремиться к нулю на
должны стремиться к нулю на  и для практических целей чем быстрее, тем лучше. Рассмотрим в качестве базисных функций вейвлеты — хорошо локализованные солитоно-подобные "маленькие волны" (дословный перевод слова wavelet).
и для практических целей чем быстрее, тем лучше. Рассмотрим в качестве базисных функций вейвлеты — хорошо локализованные солитоно-подобные "маленькие волны" (дословный перевод слова wavelet).
Как и в случае с пространством  которое полностью формировалось с помощью одной базисной функции
которое полностью формировалось с помощью одной базисной функции  сконструируем функциональное пространство
сконструируем функциональное пространство  также с помощью одного вейвлета
также с помощью одного вейвлета  Отметим, что это может быть вейвлет с одной частотой или с набором частот (frequency bands). Начнем с дискретных преобразований.
Отметим, что это может быть вейвлет с одной частотой или с набором частот (frequency bands). Начнем с дискретных преобразований.
Как же с помощью быстро стремящейся к нулю локализованной функции покрыть всю ось  Наиболее просто это можно сделать, предусмотрев систему сдвигов (переносов) вдоль оси. Пусть для простоты они будут целыми, т.е.
Наиболее просто это можно сделать, предусмотрев систему сдвигов (переносов) вдоль оси. Пусть для простоты они будут целыми, т.е. 
Введем аналог синусоидальной частоты. Для простоты и определенности запишем ее через степени двойки:  здесь
здесь  — целые числа
— целые числа 
Таким образом, с помощью дискретных масштабных преобразований  и сдвигов
и сдвигов  мы можем описать все частоты и покрыть всю ось, имея единственный базисный вейвлет
мы можем описать все частоты и покрыть всю ось, имея единственный базисный вейвлет 
Напомним определение нормы:

(звездочка обозначает комплексное сопряжение). Следовательно,

т.е. если вейвлет  имеет единичную норму, то все вейвлеты семейства
имеет единичную норму, то все вейвлеты семейства  вида
вида

также нормированы на единицу, т.е. 
Вейвлет  называется ортогональным, если определенное соотношением (7) семейство
называется ортогональным, если определенное соотношением (7) семейство  представляет собой ортонормированный базис функционального пространства
представляет собой ортонормированный базис функционального пространства  т.е.
т.е.

и каждая функция  может быть представлена в виде ряда
может быть представлена в виде ряда

равномерная сходимость которого в  означает, что
означает, что

Простейшим примером ортогонального вейвлета является  -вейвлет, названный так по имени предложившего его Хаара (Haar), и определяемый соотношением
-вейвлет, названный так по имени предложившего его Хаара (Haar), и определяемый соотношением

Легко видеть, что любые две функции  полученные из этого вейвлета по формуле (7) с помощью масштабных преобразований
полученные из этого вейвлета по формуле (7) с помощью масштабных преобразований  и сдвигов
и сдвигов  ортогональны и имеют единичную норму.
ортогональны и имеют единичную норму.
Сконструируем базис функционального пространства  с помощью непрерывных масштабных преобразований и переносов вейвлета
с помощью непрерывных масштабных преобразований и переносов вейвлета  с произвольными значениями базисных параметров — масштабного коэффициента а и параметра сдвига
с произвольными значениями базисных параметров — масштабного коэффициента а и параметра сдвига 

На его основе запишем интегральное вейвлет-преобразование:

Проводя дальнейшую аналогию с преобразованием Фурье, коэффициенты  разложения (8) функции
разложения (8) функции  в ряд по вейвлетам можно определить через интегральное вейвлет-преобразование:
в ряд по вейвлетам можно определить через интегральное вейвлет-преобразование:

В дальнейшем иногда вместо  для коэффициентов (амплитуд) вейвлет-преобразования используются обозначения
для коэффициентов (амплитуд) вейвлет-преобразования используются обозначения  или
или  или
или 
Итак, каждая функция из  может быть получена суперпозицией масштабных преобразований и сдвигов базисного вейвлета, т.е. является композицией "вей-влетных волн" (с коэффициентами, зависящими от номера волны (частоты, масштаба) и от параметра сдвига (времени).
может быть получена суперпозицией масштабных преобразований и сдвигов базисного вейвлета, т.е. является композицией "вей-влетных волн" (с коэффициентами, зависящими от номера волны (частоты, масштаба) и от параметра сдвига (времени).
Использование дискретного вейвлет-преобразования (дискретного частотно-временного пространства в виде целых сдвигов и растяжений по степеням двойки) позволяет провести доказательство многих положений теории вейвлетов [2-5], связанных с полнотой и ортогональностью базиса, сходимостью рядов и т.п. Доказательность этих положений необходима, например, при сжатии информации или в задачах численного моделирования, т.е. в случаях, когда важно провести разложение с минимальным числом независимых коэффициентов вейвлет-преобразования и иметь точную формулу обратного преобразования. При применении вейвлетов для анализа сигналов непрерывное вейвлет-преобразование (11) более удобно; его некоторая избыточность, связанная с непрерывным изменением масштабного коэффициента а и параметра сдвига  становится здесь положительным качеством, так как позволяет более полно и четко представить и проанализировать содержащуюся в данных информацию.
становится здесь положительным качеством, так как позволяет более полно и четко представить и проанализировать содержащуюся в данных информацию.
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
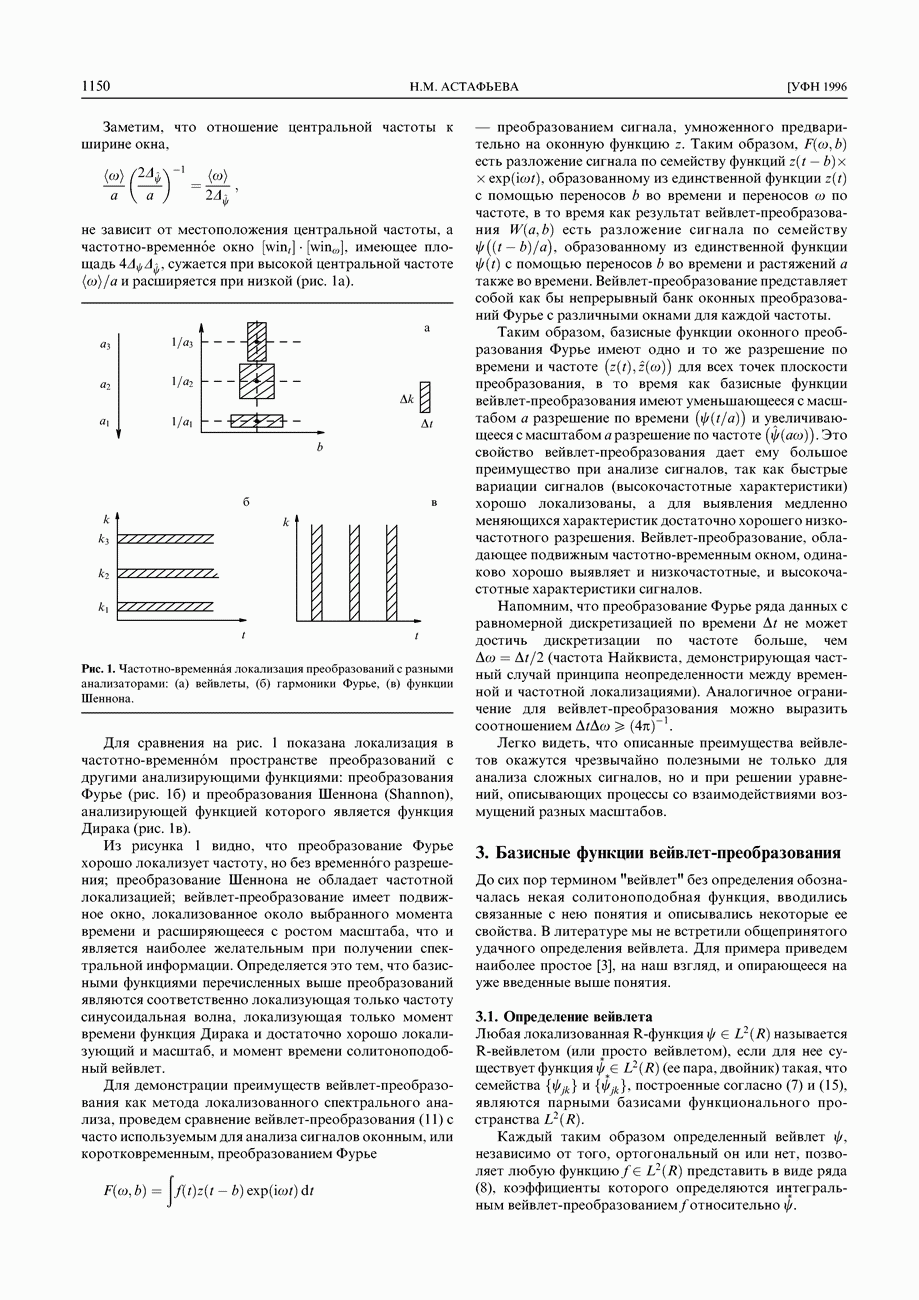
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
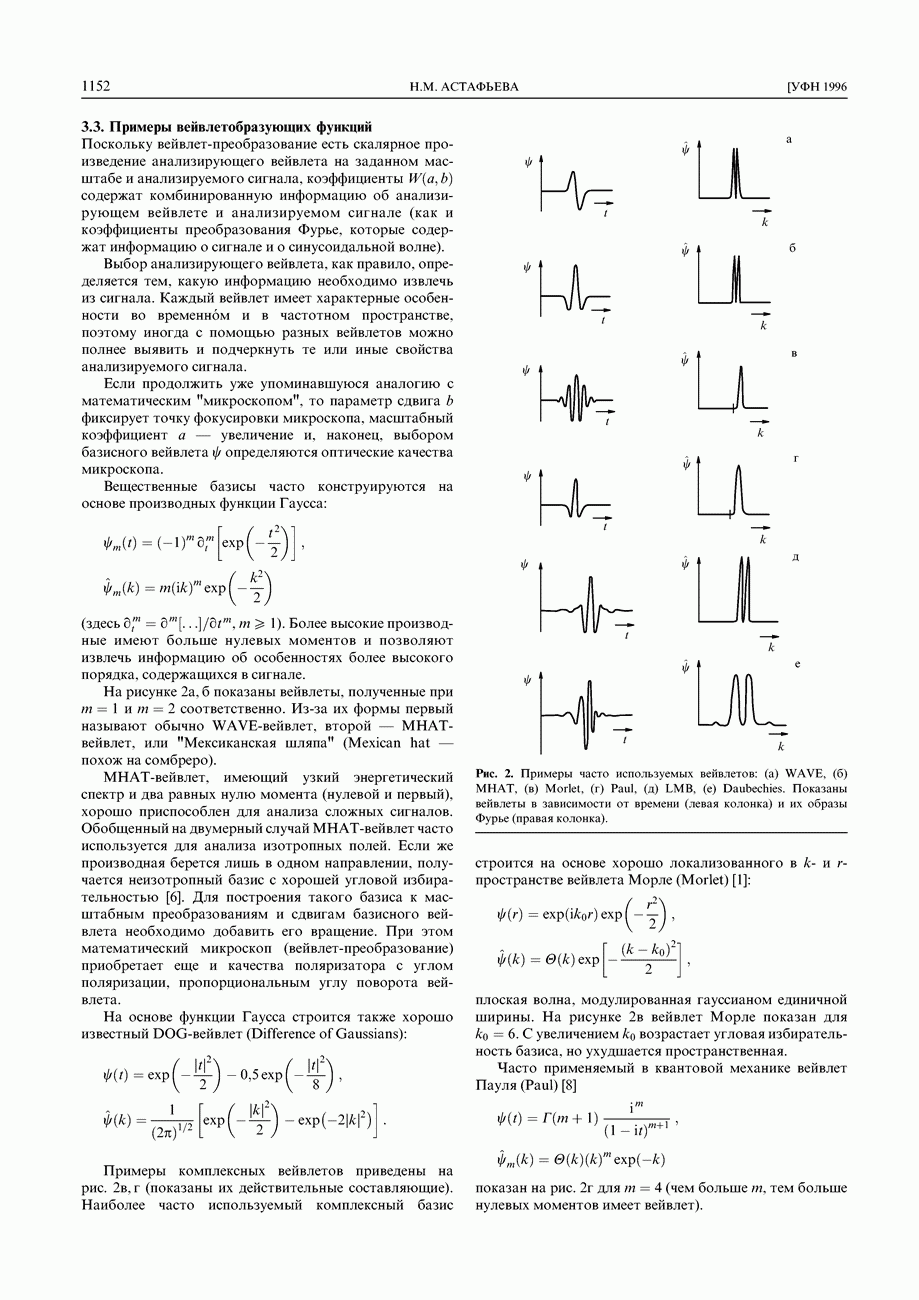
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
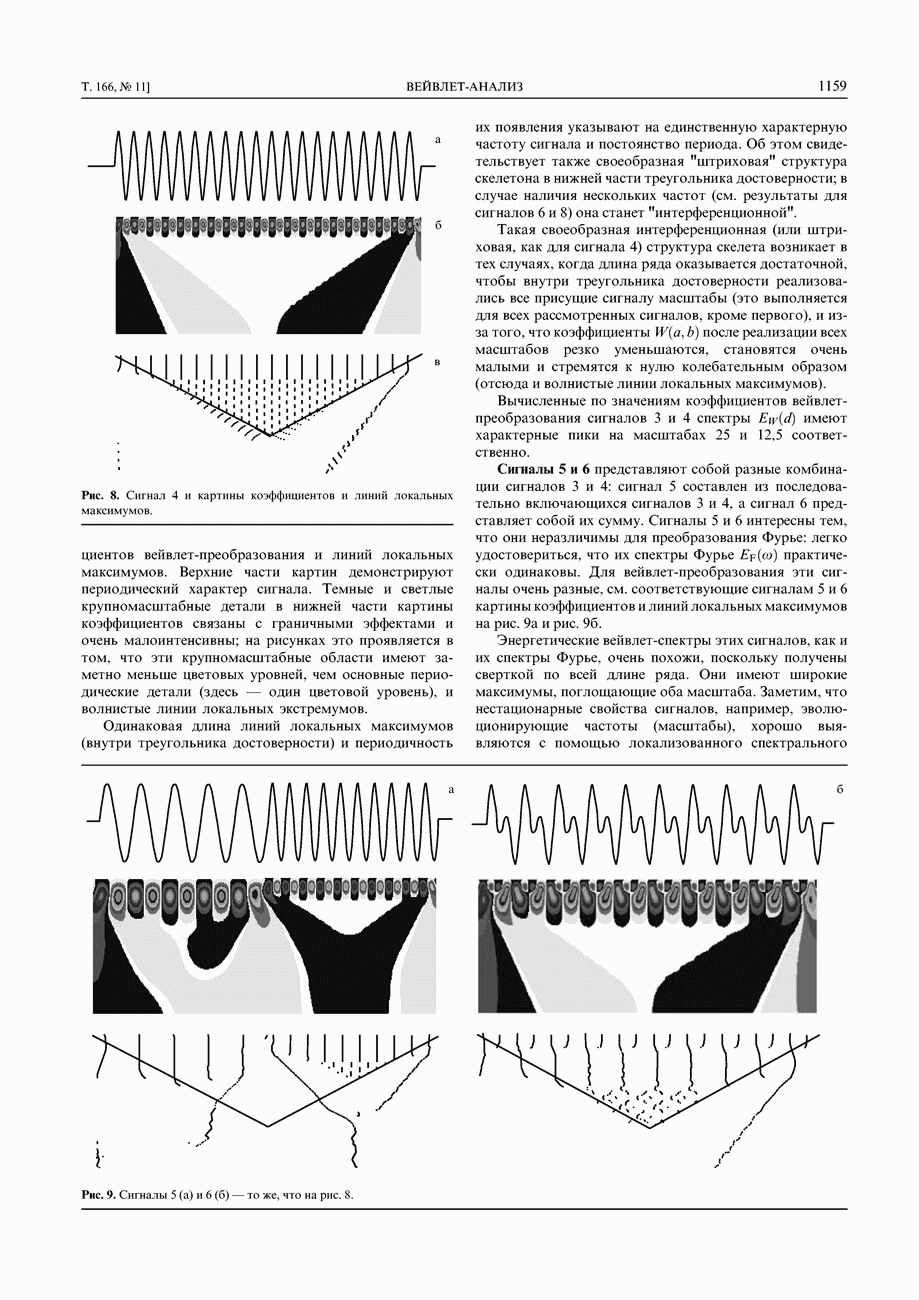
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы