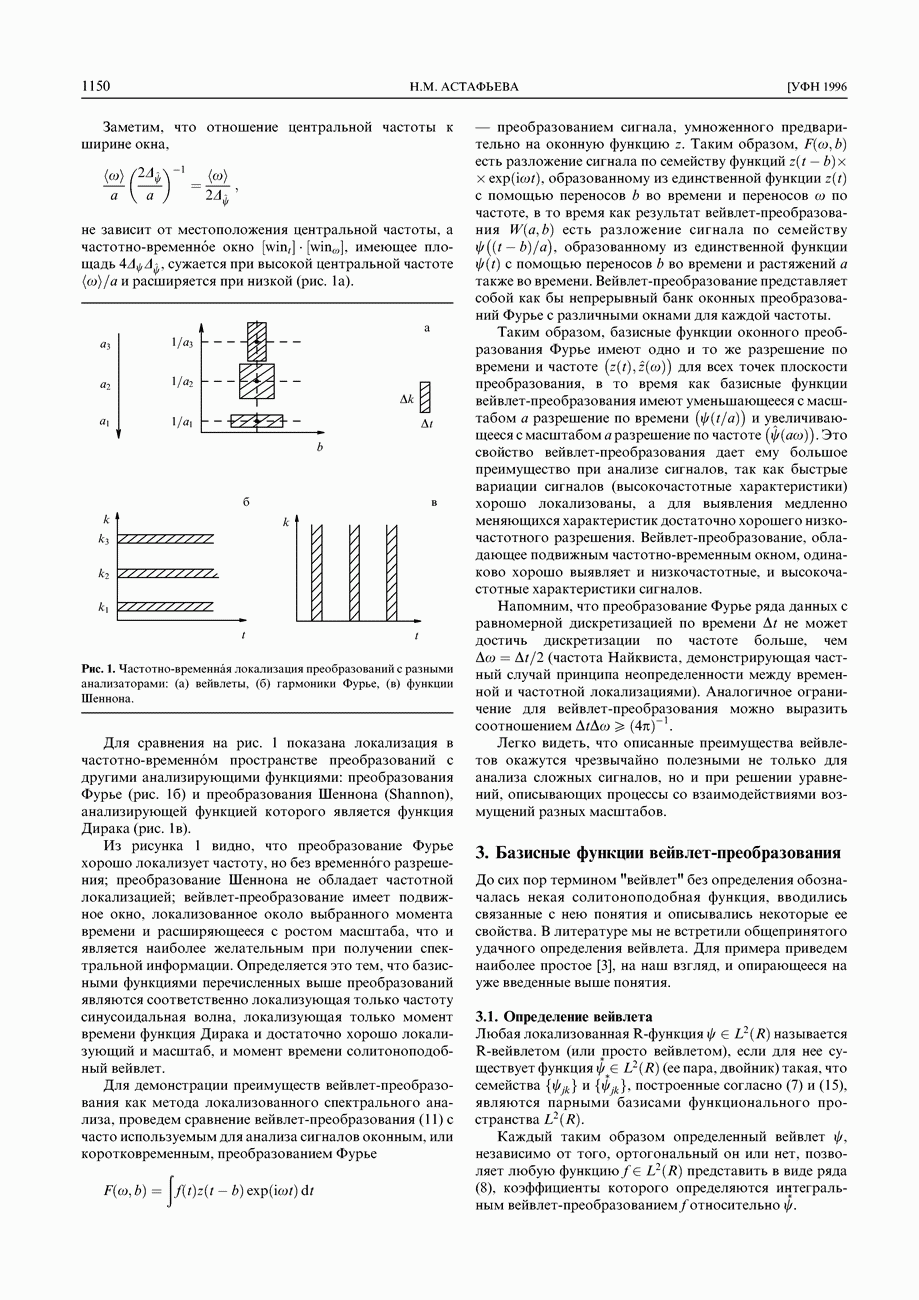
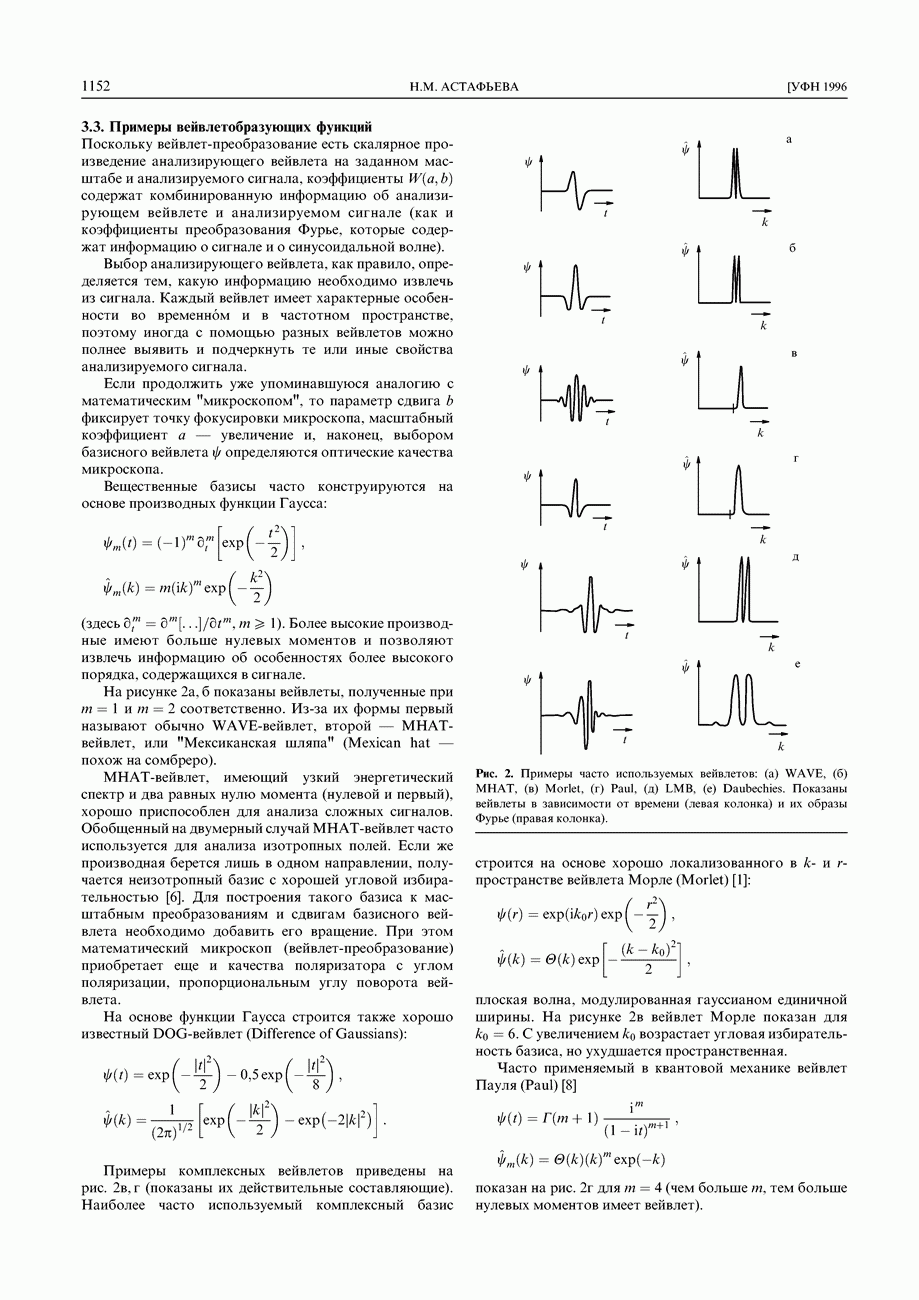
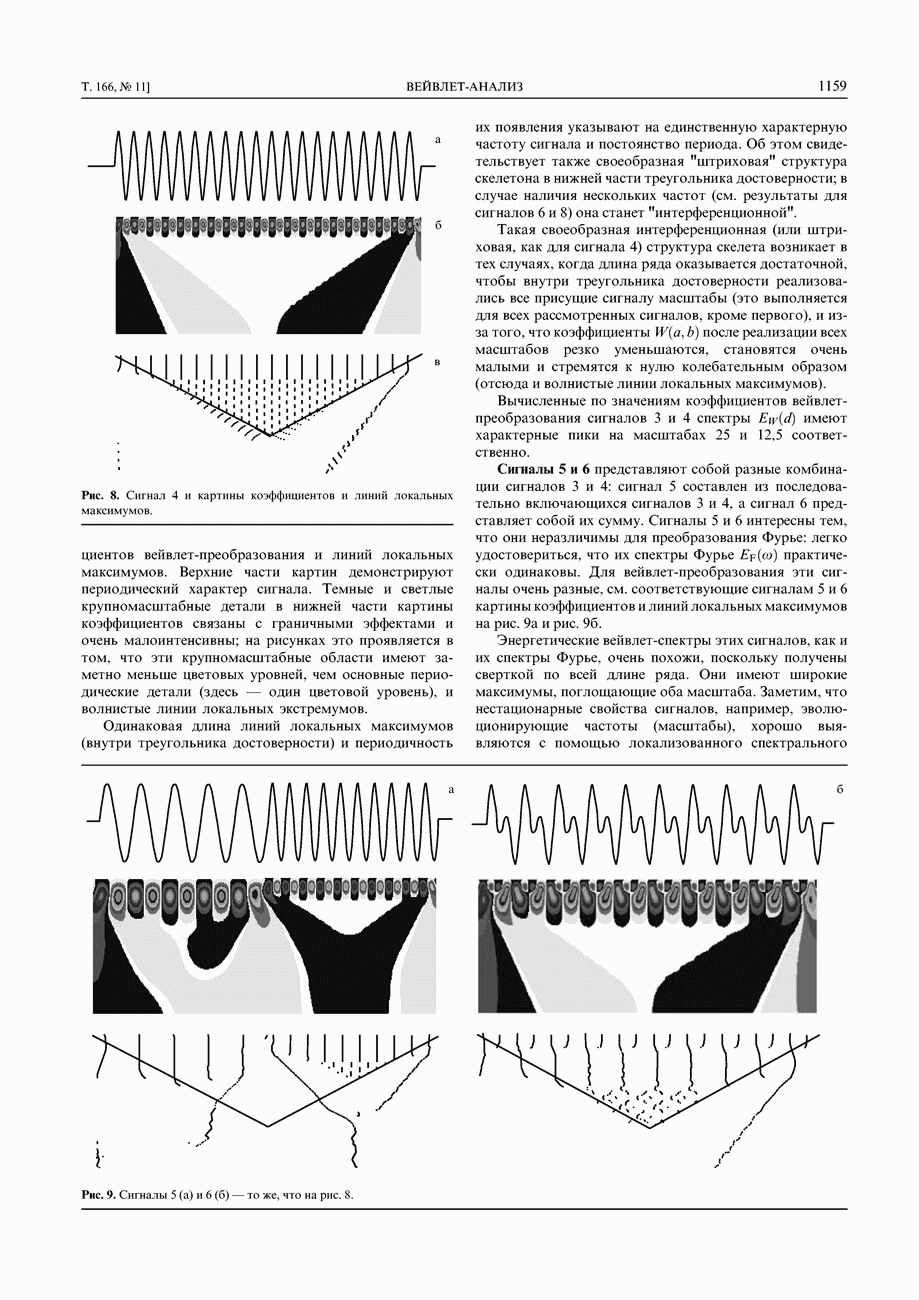
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. Признаки вейвлета
Для практического применения важно знать признаки, которыми обязательно должна обладать функция, чтобы быть вейвлетом; приведем их здесь, а также рассмотрим в качестве примеров некоторые хорошо известные функции и их соответствие этим необходимым признакам.
Локализация. Вейвлет-преобразование в отличие от преобразования Фурье использует локализованную базисную функцию. Вейвлет должен быть локализован и во временном пространстве, и по частоте.
Нулевое среднее:

Часто для приложений оказывается необходимым, чтобы не только нулевой, но и все первые  моментов были равны нулю:
моментов были равны нулю:

Такой вейвлет называется вейвлетом  порядка. Обладающие большим числом нулевых моментов вейвлеты позволяют, игнорируя наиболее регулярные полиномиальные составляющие сигнала, анализировать мелкомасштабные флуктуации и особенности высокого порядка.
порядка. Обладающие большим числом нулевых моментов вейвлеты позволяют, игнорируя наиболее регулярные полиномиальные составляющие сигнала, анализировать мелкомасштабные флуктуации и особенности высокого порядка.
Ограниченность:

Оценка хорошей локализации и ограниченности может быть записана в виде

здесь  — доминантная частота вейвлета, число
— доминантная частота вейвлета, число  должно быть возможно большим.
должно быть возможно большим.
Автомодельность базиса. Характерным признаком базиса вейвлет-преобразования является его самоподобие. Все вейвлеты данного семейства  имеют то же число осцилляций, что и базисный вейвлет
имеют то же число осцилляций, что и базисный вейвлет  поскольку получены из него посредством масштабных преобразований и сдвигов. Благодаря этому вейвлет-преобразование с успехом применяется для анализа фрактальных сигналов (см., например, [7]).
поскольку получены из него посредством масштабных преобразований и сдвигов. Благодаря этому вейвлет-преобразование с успехом применяется для анализа фрактальных сигналов (см., например, [7]).
Сказанное выше можно проиллюстрировать примерами из [6], где приведен ряд функций и их образов Фурье. Для сравнения среди приведенных функций есть и вейвлеты, и функции, которые по тем или иным причинам вейв летами быть не могут.
Например,  -функция и синус не удовлетворяют необходимому условию одновременной локализации во временном пространстве и в пространстве частот: хорошо локализованная в
-функция и синус не удовлетворяют необходимому условию одновременной локализации во временном пространстве и в пространстве частот: хорошо локализованная в  -пространстве
-пространстве  -функция не обладает этим свойством в
-функция не обладает этим свойством в  -пространстве; наоборот, хорошо локализованный в
-пространстве; наоборот, хорошо локализованный в  -пространстве синус не обладает этим свойством в
-пространстве синус не обладает этим свойством в  -пространстве.
-пространстве.
Функция Табора

представляет собой модулированную функцию Гаусса с четырьмя параметрами: сдвиг  стандартное (среднеквадратичное) отклонение а, частота модуляции
стандартное (среднеквадратичное) отклонение а, частота модуляции  и фазовый сдвиг Разложение по функциям Табора является разложением по модулированным фрагментам синусоид. Длина фрагментов для всех частот постоянна, что дает различное число осцилляций для разных гармоник. Отсюда следует, что достаточно хорошо локализованная и в
и фазовый сдвиг Разложение по функциям Табора является разложением по модулированным фрагментам синусоид. Длина фрагментов для всех частот постоянна, что дает различное число осцилляций для разных гармоник. Отсюда следует, что достаточно хорошо локализованная и в  и в
и в  -пространстве функция Табора не может быть базисной функцией вейвлет-преобразования, поскольку построенный на ее основе базис не обладает свойством самоподобия.
-пространстве функция Табора не может быть базисной функцией вейвлет-преобразования, поскольку построенный на ее основе базис не обладает свойством самоподобия.
HAAR-вейвлет (см. формулу (9)) — пример ортогонального дискретного вейвлета, порождающего ортонормированный базис. Недостатками этого вейвлета являются негладкость — резкие границы в  -пространстве, вследствие чего возникают бесконечные (убывающие как
-пространстве, вследствие чего возникают бесконечные (убывающие как  "хвосты" в
"хвосты" в  -пространстве, а также несимметрия формы. Для некоторых приложений эти недостатки несущественны, а иногда односторонность вейвлета даже становится достоинством. Часто применяется очень похожий, также дискретный, но симметричный
-пространстве, а также несимметрия формы. Для некоторых приложений эти недостатки несущественны, а иногда односторонность вейвлета даже становится достоинством. Часто применяется очень похожий, также дискретный, но симметричный  -вейвлет, более известный под названием "Французская шляпа" (French hat — похож на цилиндр):
-вейвлет, более известный под названием "Французская шляпа" (French hat — похож на цилиндр):

здесь  — функция Хевисайда
— функция Хевисайда  при
при  FHAT-вейвлет, нерегулярный во временном пространстве и недостаточно быстро спадающий в пространстве частот, и
FHAT-вейвлет, нерегулярный во временном пространстве и недостаточно быстро спадающий в пространстве частот, и  -вейвлет (вейвлет Литтлвуда-Пели (Littlewood & Paley, см. [6])), наоборот, имеющий резко очерченные границы в
-вейвлет (вейвлет Литтлвуда-Пели (Littlewood & Paley, см. [6])), наоборот, имеющий резко очерченные границы в  -пространстве и плохо спадающий в
-пространстве и плохо спадающий в  -пространстве, можно считать предельными случаями, между которыми находятся практически все вейвлеты.
-пространстве, можно считать предельными случаями, между которыми находятся практически все вейвлеты.
| << Предыдущий параграф | Следующий параграф >> |
- Вейвлет-анализ: основы теории и примеры применения
- 1. Введение
- 2. От преобразования Фурье к вейвлет-преобразованию
- 2.2. Разложение по вейвлетам
- 2.3. Обратное вейвлет-преобразование
- 2.4. Частотно-временная локализация
- 3. Базисные функции вейвлет-преобразования
- 3.2. Признаки вейвлета
- 3.3. Примеры вейвлетобразующих функций
- 4. Свойства и возможности вейвлет-преобразования
- 4.2. Свойства вейвлет-преобразования
- 4.3. Некоторые возможности вейвлет-анализа
- 5. Применение вейвлет-преобразования к модельным сигналам
- 5.2. Сигнал с особенностью
- 5.3. Фрактальное множество
- 6. Анализ временных метеорологических рядов
- 6.2. 500 лет из жизни Эль-Ниньо
- 6.3. Среднемесячные значения индекса Южного Колебания
- 6.4. Суточные значения индекса Южного Колебания
- 6.5. Глобальные температуры и ЮКЭН
- 7. Заключение
- Список литературы