| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14. Моделирование потоков заявок
Рассмотрим способы моделирования на ЭВМ потоков заявок, поступающих в систему массового обслуживания. Сначала остановимся на достаточно простом и вместе с тем наиболее распространенном случае, когща в систему поступает ординарный стационарный поток однородных событий с ограниченным последействием (поток типа Пальма).
Любой поток типа Пальма может быть задан функцией плотности  случайных интервалов
случайных интервалов  между последовательными моментами — поступления заявок. Для моделирования его на ЭВМ достаточно построить необходимое число реализаций потока, т. е. таких неслучайных последовательностей
между последовательными моментами — поступления заявок. Для моделирования его на ЭВМ достаточно построить необходимое число реализаций потока, т. е. таких неслучайных последовательностей  моментов
моментов
поступления заявок в систему, интервалы между которыми  являлись бы возможными значениями случайных величин
являлись бы возможными значениями случайных величин  описываемых функцией плотности
описываемых функцией плотности 
Процедура построения последовательности  состоит в следующем. Сначала формируется
состоит в следующем. Сначала формируется  Функция плотности
Функция плотности  может быть определена через
может быть определена через  по формуле Пальма (4.4). Тогда, исходя из наличия в ЭВМ электронного или алгоритмического датчика случайных чисел
по формуле Пальма (4.4). Тогда, исходя из наличия в ЭВМ электронного или алгоритмического датчика случайных чисел  с равномерным распределением в интервале (0,1), приступаем к формированию
с равномерным распределением в интервале (0,1), приступаем к формированию  Для этого одним из способов, рассмотренных в главе П, преобразуем случайное число
Для этого одним из способов, рассмотренных в главе П, преобразуем случайное число  в случайное число
в случайное число  имеющее функцию плотности
имеющее функцию плотности  Получив
Получив  полагаем
полагаем

Далее переходим к формированию  Очередное случайное число
Очередное случайное число  аналогичным образом преобразуем в случайное число
аналогичным образом преобразуем в случайное число  имеющее функцию плотности
имеющее функцию плотности  Получив
Получив  полагаем
полагаем

В дальнейшем процедура получения любого  совпадает с процедурой формирования
совпадает с процедурой формирования  т. е. очередное случайное число преобразуется в случайное число
т. е. очередное случайное число преобразуется в случайное число  имеющее функцию плотности
имеющее функцию плотности  и
и

Рассмотрим некоторые примеры, часто встречающиеся при решении практических задач методом статистического моделирования.
Пример 1. Простейший (пауссоновский) поток.
Как отмечалось выше, простейший (пауссоновский) поток является стационарным ординарным потоком однородных событий без последействия, т. е. одним из возможных частных случаев потоков типа Пальма. Функция плотности  для простейшего потока имеет вид показательного распределения (4.6):
для простейшего потока имеет вид показательного распределения (4.6):

где  — интенсивность потока, определяющая среднее значение числа заявок, поступающих в единицу времени.
— интенсивность потока, определяющая среднее значение числа заявок, поступающих в единицу времени.
Чтобы определить функцию плотности  для первого интервала, воспользуемся формулой Пальма.
для первого интервала, воспользуемся формулой Пальма.

После несложных вычислений получаем:

Отсюда следует, что функция плотности первого интервала для простейшего потока имеет тот же вид, что и  Этим свойством в общем случае, не обладают другие потоки типа Пальма.
Этим свойством в общем случае, не обладают другие потоки типа Пальма.
Таким образом, для формирования реализаций простейшего потока необходимо иметь последовательность случайных чисел  имеющих показательное распределение (4.6) с параметром К. Методику получения такой последовательности мы рассматривали в главе II. В соответствии с (2.15) случайные числа
имеющих показательное распределение (4.6) с параметром К. Методику получения такой последовательности мы рассматривали в главе II. В соответствии с (2.15) случайные числа  могут быть получены по формуле
могут быть получены по формуле

где  — случайные числа с равномерным распределением в интервале (0,1).
— случайные числа с равномерным распределением в интервале (0,1).
Последовательность моментов поступления заявок  будет следующей:
будет следующей:

Пример 2. Поток с равномерным распределением интервалов 
Функция плотности рассматриваемого потока имеет вид равномерного распределения:

Можно показать, что среднее значение (математическое ожидание) случайной величины  равно
равно  Поэтому среднее число заявок, поступивших в единицу времени (интенсивность потока):
Поэтому среднее число заявок, поступивших в единицу времени (интенсивность потока):

Определим функцию плотности  для первого интервала. По формуле Пальма аналогично формуле (4.11):
для первого интервала. По формуле Пальма аналогично формуле (4.11):

Заметим, что среднее значение длительности первого интервала может быть получено как математическое ожидание случайной величины, имеющей функцию плотности (4.16):

Перейдем к формированию первого интервала  Для этого, имея случайные числа
Для этого, имея случайные числа  с равномерным законом распределения в интервале (0,1), необходимо получить случайное число
с равномерным законом распределения в интервале (0,1), необходимо получить случайное число  соответствующее функции плотности (4.16). Преобразуем соотношение (4.16) следующим образом. Подставим в него вместо величины
соответствующее функции плотности (4.16). Преобразуем соотношение (4.16) следующим образом. Подставим в него вместо величины  ее значение
ее значение  из равенства (4.15). Тогда можно записать функцию плотности
из равенства (4.15). Тогда можно записать функцию плотности 

Легко усмотреть, что  в таком виде совпадает с функцией плотности (2.16). Поэтому для определения
в таком виде совпадает с функцией плотности (2.16). Поэтому для определения  можно воспользоваться формулой (2.20):
можно воспользоваться формулой (2.20):

Формирование  сводится к получению случайных чисел, имеющих равномерное распределение в интервале
сводится к получению случайных чисел, имеющих равномерное распределение в интервале  соответствующих функций плотности (4.14). Для этого достаточно случайные числа
соответствующих функций плотности (4.14). Для этого достаточно случайные числа  с равномерным распределением в интервале (0,1) привести к интервалу
с равномерным распределением в интервале (0,1) привести к интервалу 

Последовательность моментов поступления заявок рассматриваемого потока определяется системой уравнений (4.13).
Аналогично могут быть описаны процедуры формирования других потоков однородных событий с ограниченным последействием. Соответствующие соотношения приводятся в работах [3], [4] и др.
Необходимо отметить, что потоки, рассмотренные в примерах 1 и 2, отличаются благоприятной особенностью: интегралы в формуле Пальма и формулах преобразования случайных чисел берутся в конечном виде. В общем случае эти интегралы могут оказаться неберущимися. Кроме того, функции плотности  иногда задаются таблично по (результатам обработки статистического материала. На практике в такого рода ситуациях пользуются приближенными методами. Интеграл в формуле Пальма вычисляется обычно для заданного набора
иногда задаются таблично по (результатам обработки статистического материала. На практике в такого рода ситуациях пользуются приближенными методами. Интеграл в формуле Пальма вычисляется обычно для заданного набора  численными методами. Это не оказывается существенно на объеме вычислений, так как формула Пальма применяется только один раз для данного потока. Преобразование случайных чисел выполняется, как правило, методом кусочной аппроксимации функции плотности в соответствии с соотношениями (2.23), (2.24) и (2.25).
численными методами. Это не оказывается существенно на объеме вычислений, так как формула Пальма применяется только один раз для данного потока. Преобразование случайных чисел выполняется, как правило, методом кусочной аппроксимации функции плотности в соответствии с соотношениями (2.23), (2.24) и (2.25).
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ (МОНТЕ КАРЛО)
- 2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
- 3. Кратные интегралы
- 4. Требуемое количество операций
- Глава II. ПОЛУЧЕНИЕ И ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ
- 6. Получение случайных чисел с заданным законом распределения
- 7. Приближенные способы преобразования случайных чисел
- 8. Моделирование случайных векторов
- Глава III. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
- 10. Этапы формализации реальных сложных систем
- 11. Операторная схема моделирующего алгоритма
- 12. Метод статистического моделирования как аппарат анализа сложных систем
- Глава IV. СТАТИСТИЧЕСКИЕ МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
- 13. Понятие системы массового обслуживания
- 14. Моделирование потоков заявок
- 15. Моделирование одноканальной системы массового обслуживания
- 16. Моделирование многоканальной системы
- 17. Модификаций систем массового обслуживания
- Глава V. МОДЕЛИРОВАНИЕ АВТОМОБИЛЬНОГО ДВИЖЕНИЯ
- 19. Описание потока автомобилей
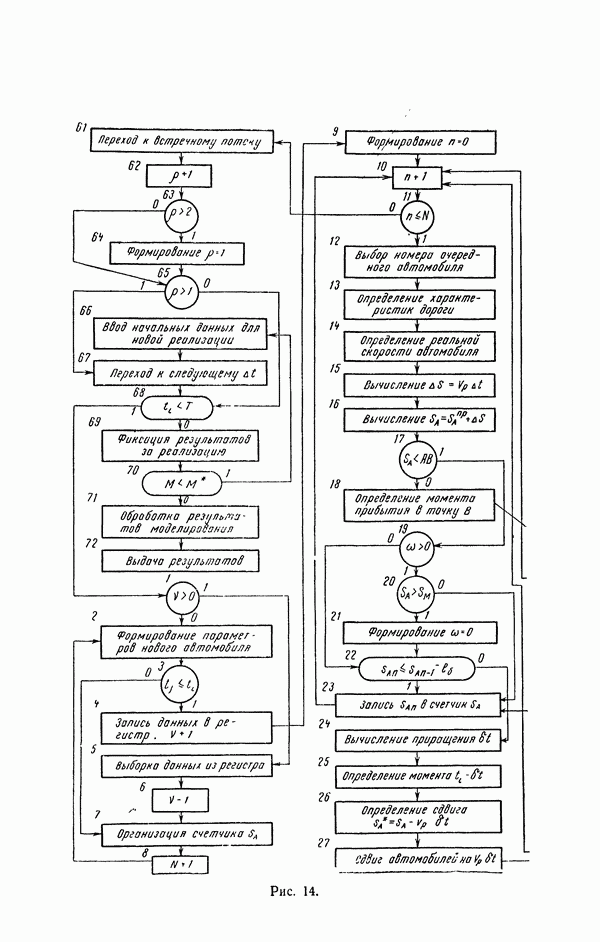
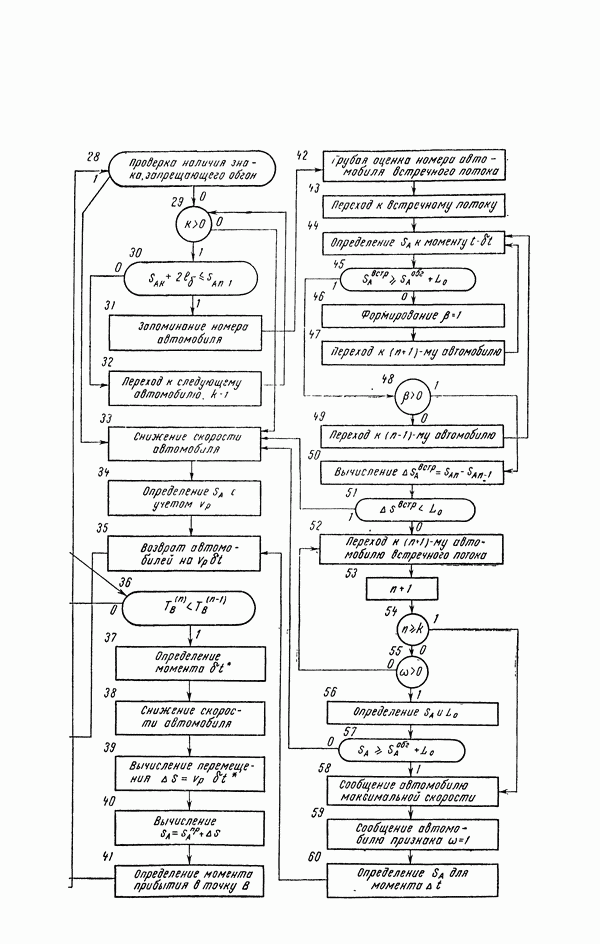
- 20. Структура моделирующего алгоритма
- 21. Исходные данные и результаты моделирования