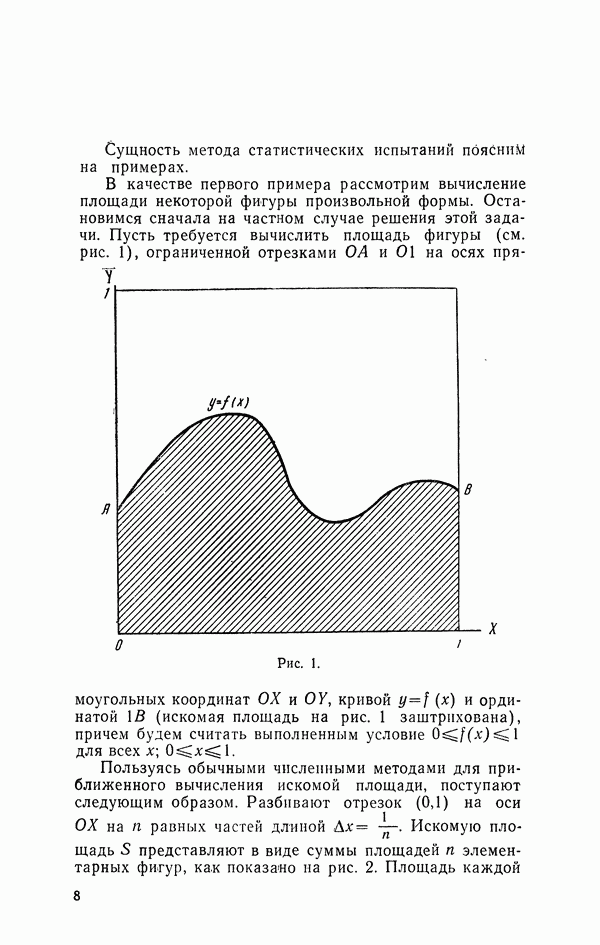
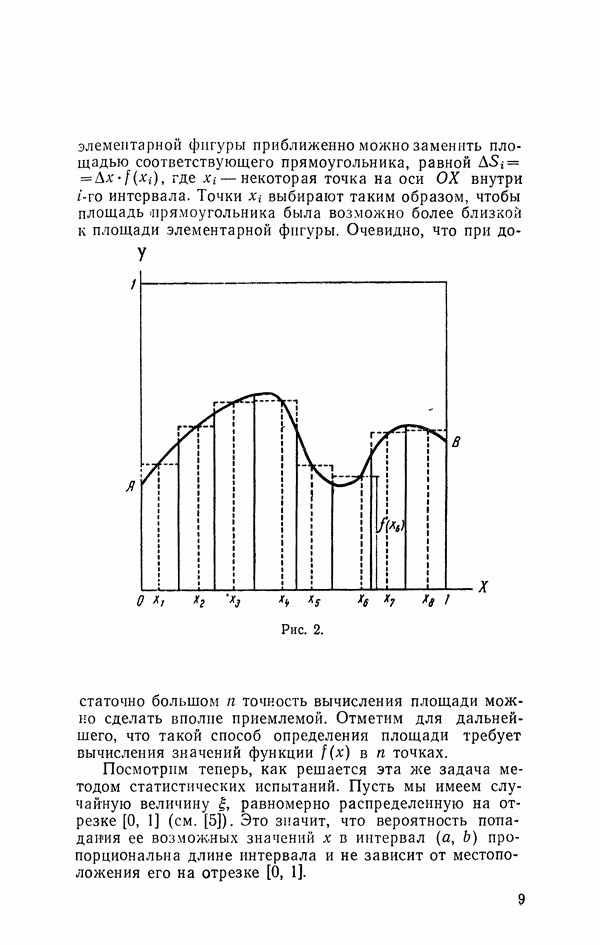
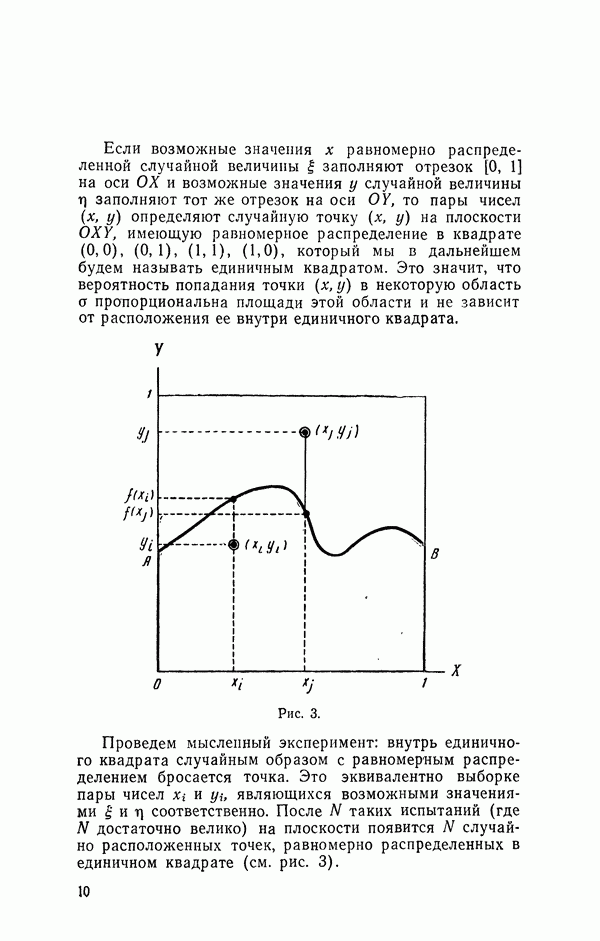
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Кратные интегралы
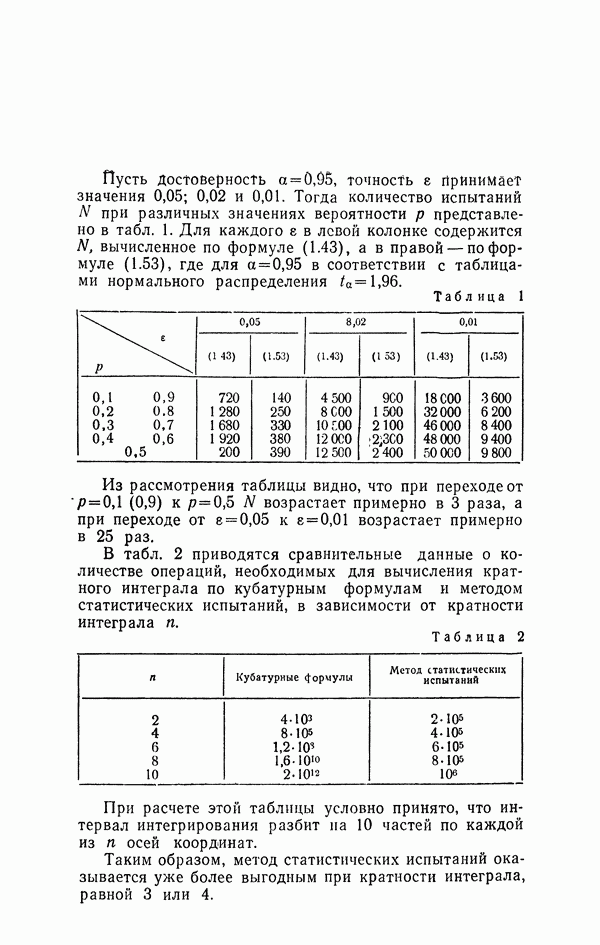
Рассмотрим приемы вычисления интеграла методом статистических испытаний с точки зрения целесообразности их применения для вычисления многократных интегралов.
Методику подхода к вычислению многократных интегралов проследим на примере интеграла

по ограниченной замкнутой области  заключенной внутри
заключенной внутри  - мерного параллелепипеда
- мерного параллелепипеда

Заменой переменных

приведем интеграл (1.23) к виду

где

Область интегрирования целиком заключена внутри  -мерного единичного куба.
-мерного единичного куба.
Для вычисления интеграла применим уже изложенный метод (см. стр. 12). Изменением масштаба по оси  преобразуем вычисляемый интеграл
преобразуем вычисляемый интеграл

где  — минимальное,
— минимальное,  максимальное значение
максимальное значение  по области со.
по области со.

и

где

Будем рассматривать вычисляемый интеграл как некоторый объем в  -мерном пространстве:
-мерном пространстве:

Координаты случайной точки в этом пространстве имеют вид совокупности  случайных чисел
случайных чисел

равномерно распределенных в интервале (0,1). Проведем N испытаний, состоящих в заполнении  - мерного единичного куба равномерно распределенными случайными точками. Будем проверять принадлежность этих точек объему V посредством неравенства
- мерного единичного куба равномерно распределенными случайными точками. Будем проверять принадлежность этих точек объему V посредством неравенства

аналогичного неравенству (1.2). По окончании эксперимента получим искомый объем

Вычисляя интеграл (1.23) как среднее значение функции, поступаем следующим образом. Выбираем последовательность  чисел
чисел

равномерно распределенных в интервале (0,1), причем точки  не принадлежащие области со, в расчет не принимаются. Получив N точек
не принадлежащие области со, в расчет не принимаются. Получив N точек  принадлежащих области
принадлежащих области  , вычисляем среднее значение
, вычисляем среднее значение

функции  по области
по области  . Затем определяем значение интеграла (1.23)
. Затем определяем значение интеграла (1.23)

где — объем области 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ (МОНТЕ КАРЛО)
- 2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
- 3. Кратные интегралы
- 4. Требуемое количество операций
- Глава II. ПОЛУЧЕНИЕ И ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ
- 6. Получение случайных чисел с заданным законом распределения
- 7. Приближенные способы преобразования случайных чисел
- 8. Моделирование случайных векторов
- Глава III. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
- 10. Этапы формализации реальных сложных систем
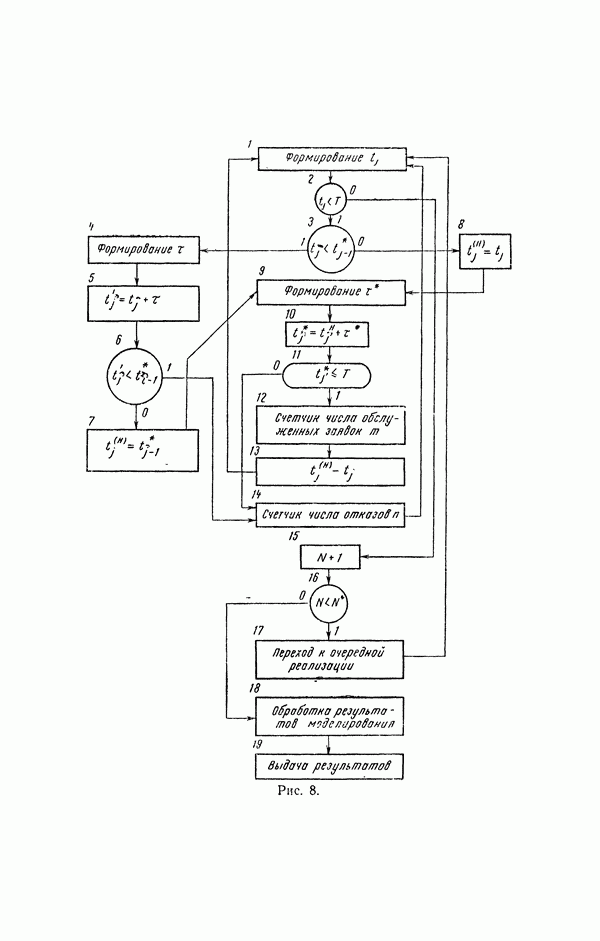
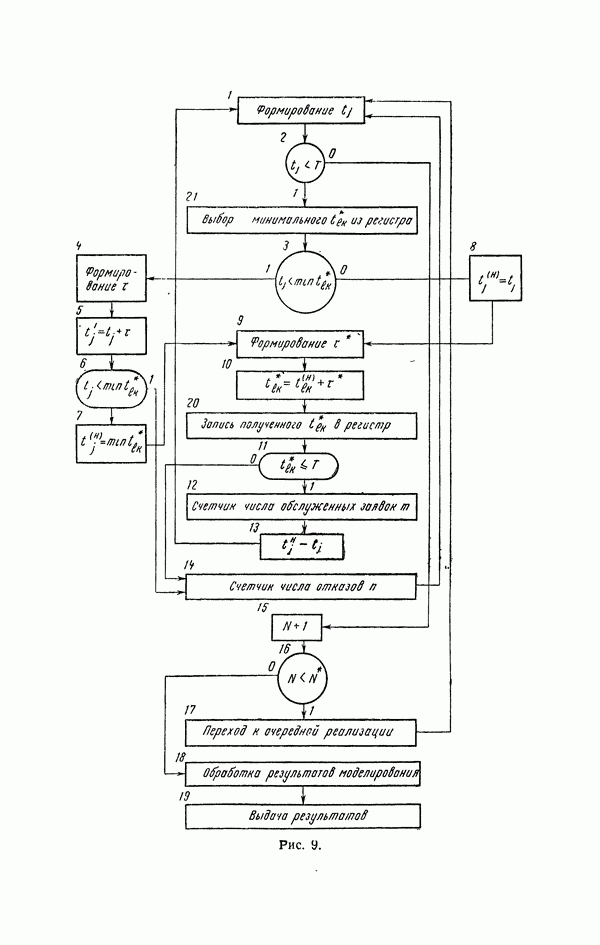
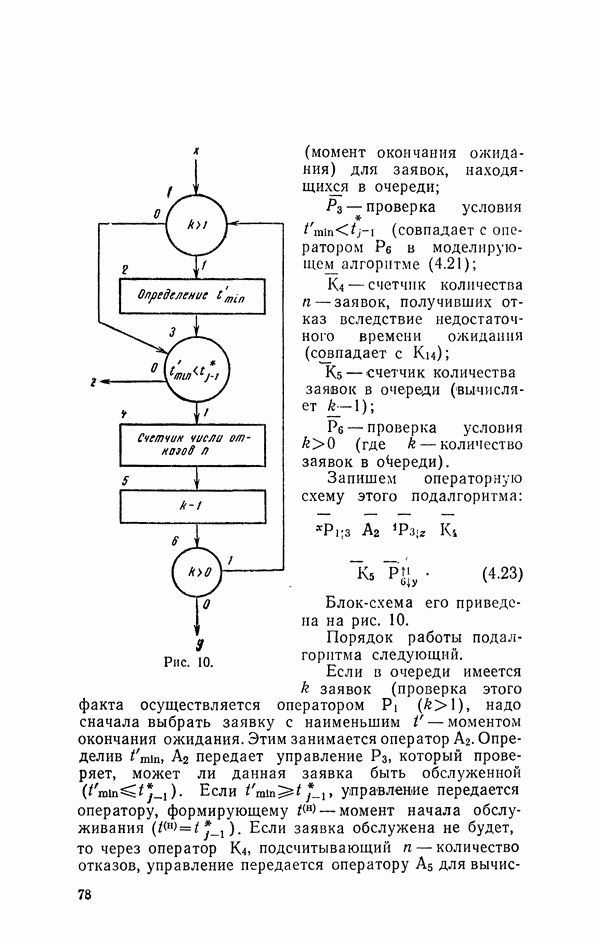
- 11. Операторная схема моделирующего алгоритма
- 12. Метод статистического моделирования как аппарат анализа сложных систем
- Глава IV. СТАТИСТИЧЕСКИЕ МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
- 13. Понятие системы массового обслуживания
- 14. Моделирование потоков заявок
- 15. Моделирование одноканальной системы массового обслуживания
- 16. Моделирование многоканальной системы
- 17. Модификаций систем массового обслуживания
- Глава V. МОДЕЛИРОВАНИЕ АВТОМОБИЛЬНОГО ДВИЖЕНИЯ
- 19. Описание потока автомобилей
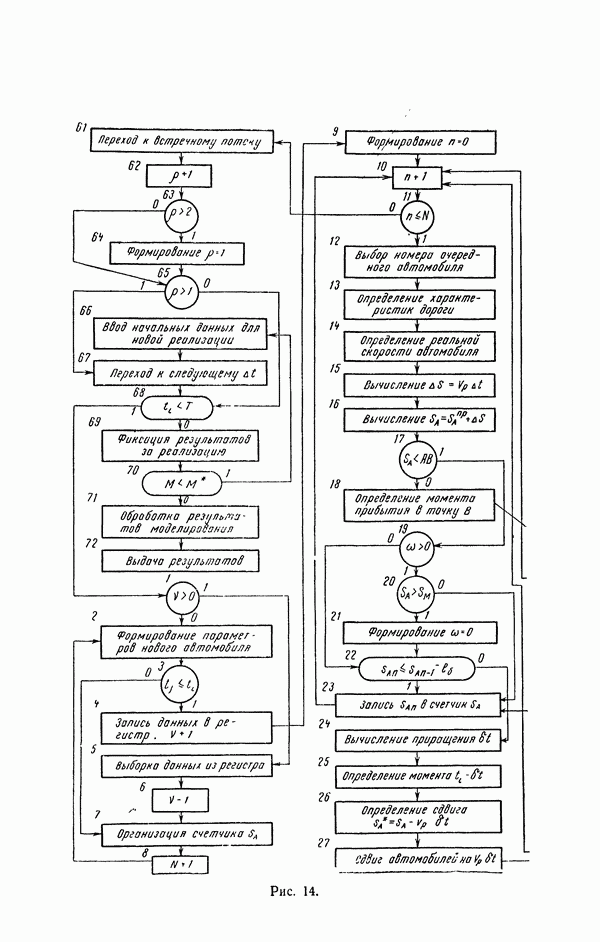
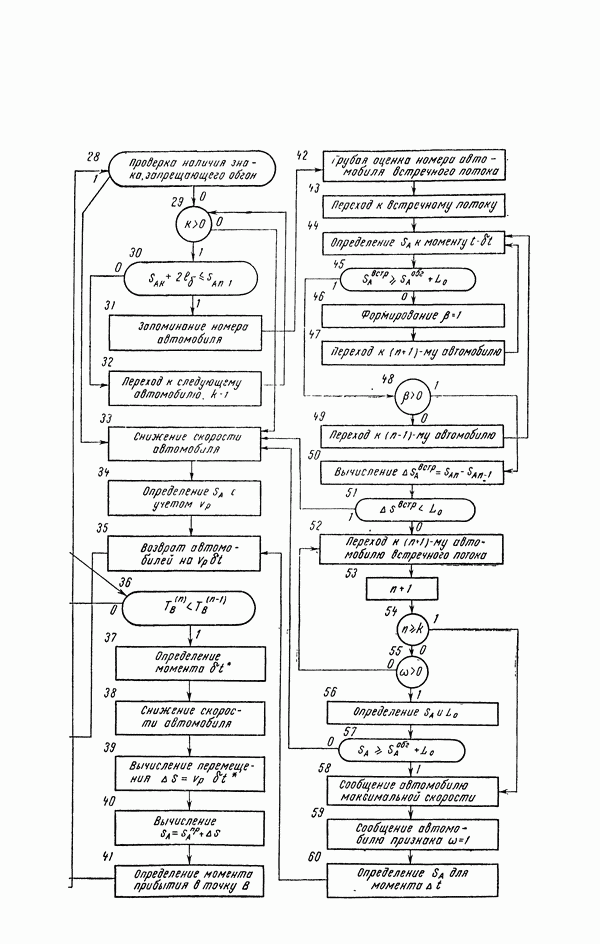
- 20. Структура моделирующего алгоритма
- 21. Исходные данные и результаты моделирования