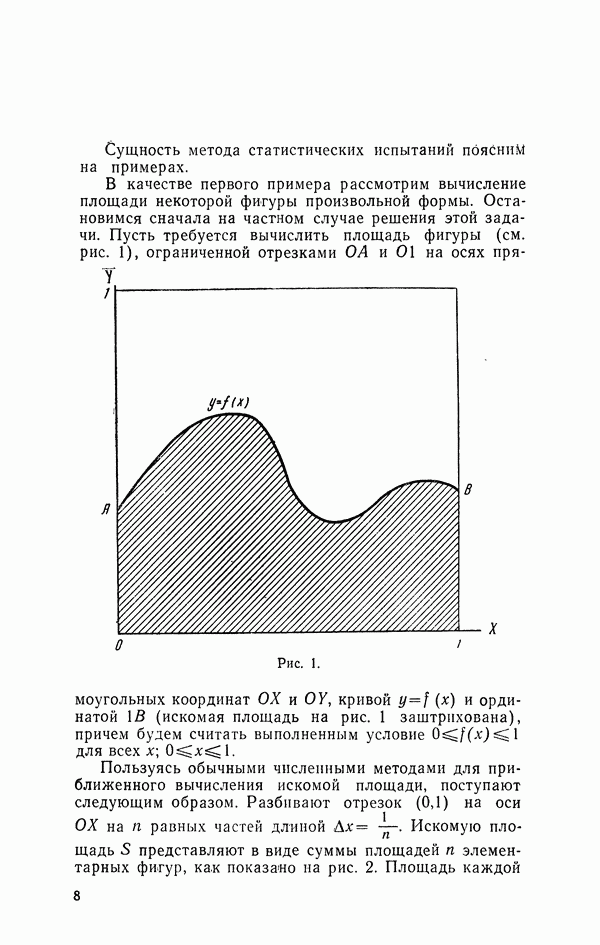
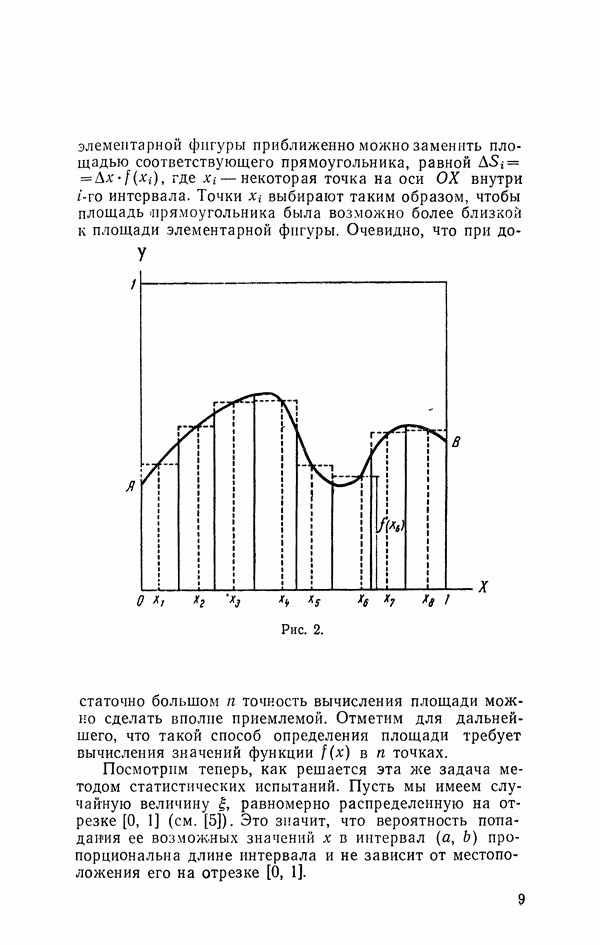
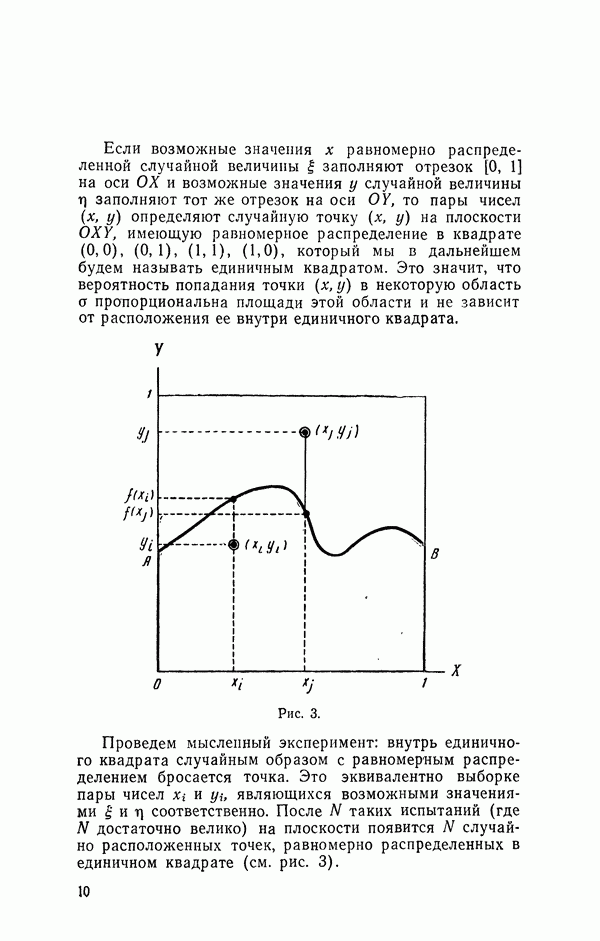
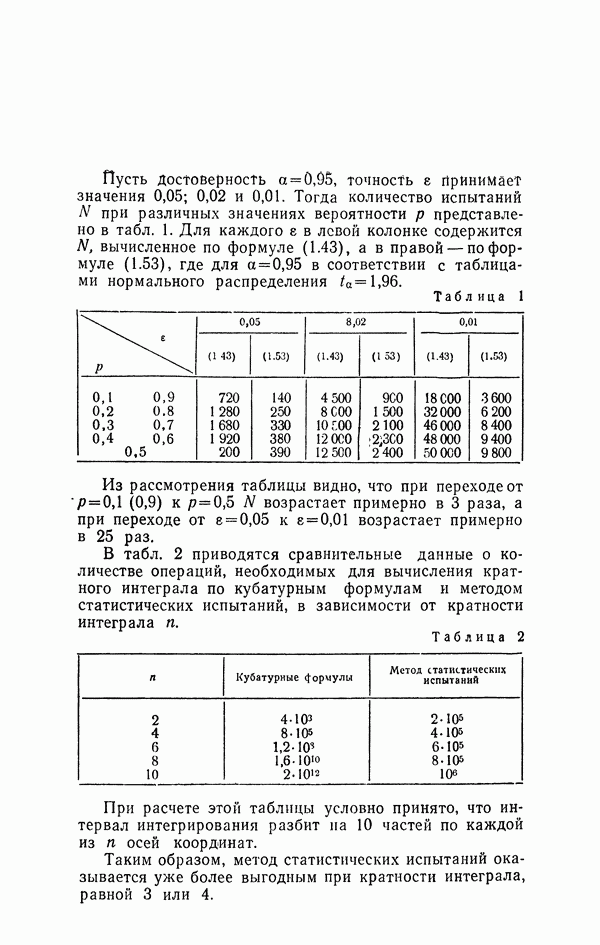
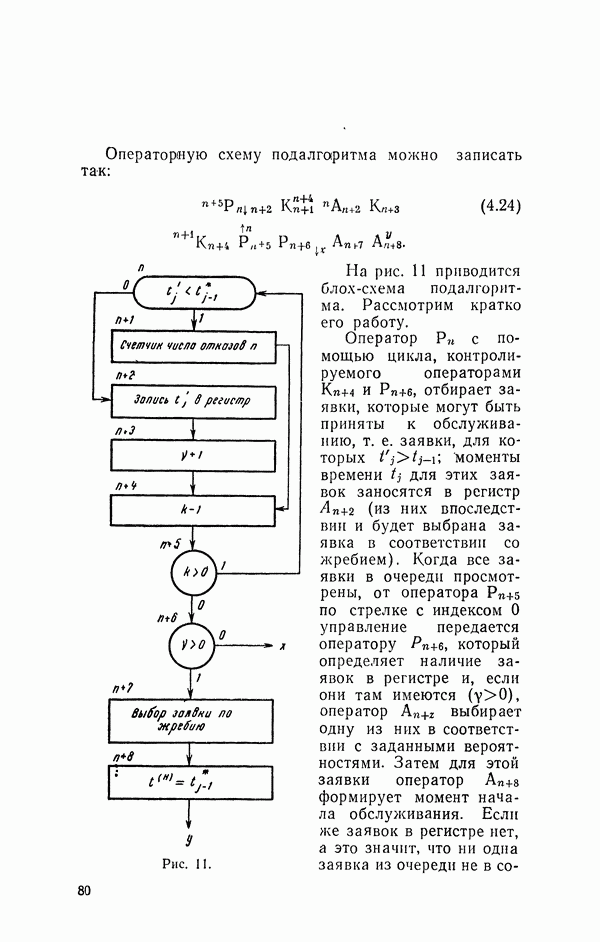
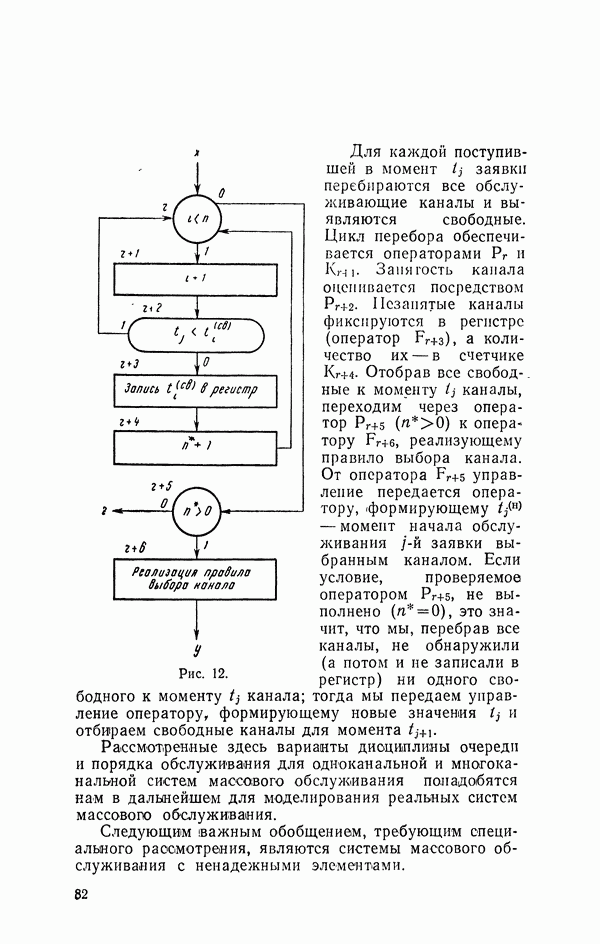
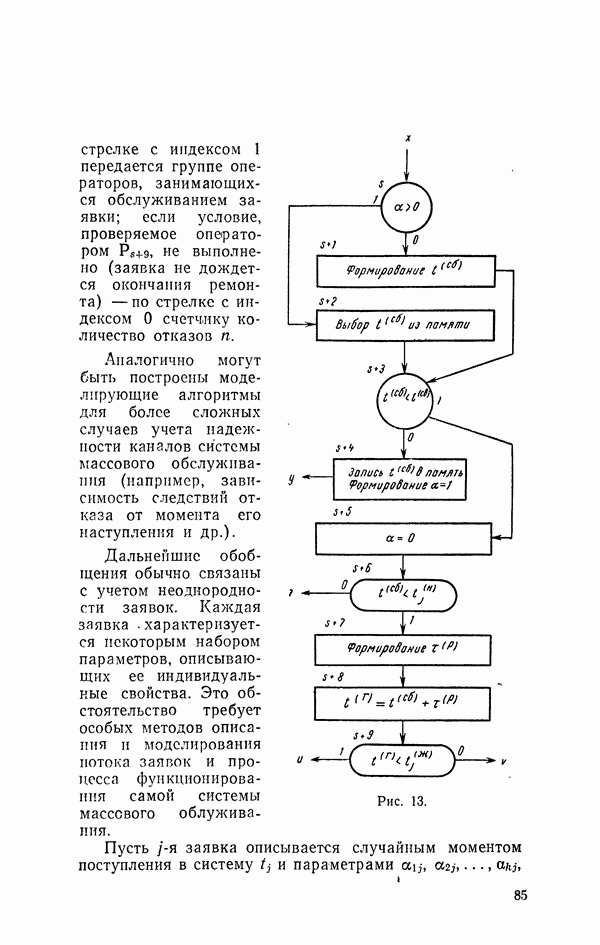
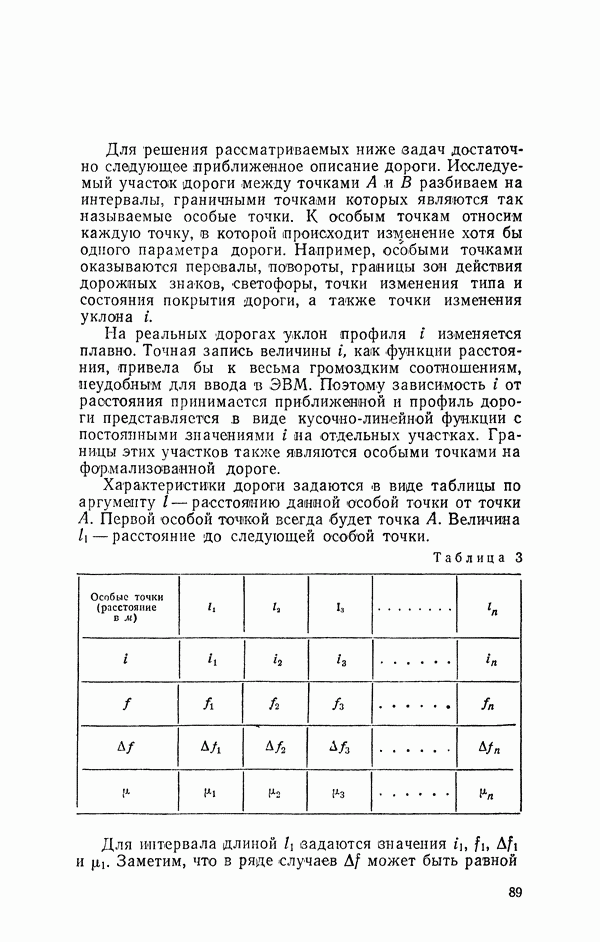
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. Приближенные способы преобразования случайных чисел
Рассмотренная процедура моделирования случайной величины с заданным законом распределения с помощью равномерно распределенной случайной величины, имеет существенные недостатки, препятствующие широкому применению этого метода на практике. Это обстоятельство послужило толчком для создания различных способов приближенного моделирования.
Существуют способы, пригодные только для моделирования случайных величин с конкретными законами распределения, существуют также универсальные способы, с помощью которых возможно моделировать законы распределения любого вида.
Приведем один из таких универсальных способов. Пусть закон распределения случайной величины  предложенной нам для моделирования, задай функцией плотности
предложенной нам для моделирования, задай функцией плотности  , возможные значения которой лежат в интервале
, возможные значения которой лежат в интервале  Если это интервал с бесконечными границами, целесообразно перейти к усеченному распределению. Представим
Если это интервал с бесконечными границами, целесообразно перейти к усеченному распределению. Представим  на участке
на участке  в виде кусочно - постоянной функции (см. рис. 6), т. е. разобьем
в виде кусочно - постоянной функции (см. рис. 6), т. е. разобьем  на
на  интервалов и будем считать
интервалов и будем считать  на каждом
на каждом

Рис. 6.
интервале постоянной; тогда случайную величину  можно представить в виде
можно представить в виде

т. е. на каждом участке  величина
величина  считается распределенной равномерно. Чтобы аппроксимировать
считается распределенной равномерно. Чтобы аппроксимировать  наиболее удобным способом, целесообразно разбить
наиболее удобным способом, целесообразно разбить  на интервалы таким образом, чтобы вероятность попадания случайной величины
на интервалы таким образом, чтобы вероятность попадания случайной величины  в любой интервал
в любой интервал  была постоянной, т. е. не зависела от номера интервала
была постоянной, т. е. не зависела от номера интервала 
Для вычисления  пользуются следующим соотношением:
пользуются следующим соотношением:

где  — количество интервалов (обычно принимается равным
— количество интервалов (обычно принимается равным  где
где  — целое положительное число).
— целое положительное число).
Процедура моделирования предполагает следующее:
1) выбирается случайное равномерно распределенное число 
2) с помощью  случайным образом выбирается интервал
случайным образом выбирается интервал 
3) берется следующее равномерно распределенное число 1 и масштабируется с целью приведения его к интервалу  становится случайной величиной, равномерно распределенной в интервале
становится случайной величиной, равномерно распределенной в интервале 
Случайное число  с требуемым законом распределения вычисляем по формуле
с требуемым законом распределения вычисляем по формуле

Интересно несколько подробнее рассмотреть процесс выборки интервала  с помощью Как известно, случайное число получается на машине в виде последовательности нулей и единиц. Если число интервалов
с помощью Как известно, случайное число получается на машине в виде последовательности нулей и единиц. Если число интервалов  равно
равно  то количество всевозможных комбинаций нулей и единиц
то количество всевозможных комбинаций нулей и единиц  -разрядного двоичного числа даст нам количество интервалов
-разрядного двоичного числа даст нам количество интервалов  т. е. каждому интервалу
т. е. каждому интервалу  можно поставить в соответствие одну и только одну комбинацию нулей и единиц
можно поставить в соответствие одну и только одну комбинацию нулей и единиц  -разрядного
-разрядного
двоичного числа. Это обстоятельство сильно упрощает методику выбора интервала 
Каждый интервал кодируется  -разрядным двоичным числом, и результаты заносятся в специальную таблицу.
-разрядным двоичным числом, и результаты заносятся в специальную таблицу.
В эту же таблицу заносятся значения  — коэффициента масштабирования.
— коэффициента масштабирования.
Таким образом, выделив  разрядов
разрядов  мы сразу определяем номер интервала
мы сразу определяем номер интервала 
Для реализации изложенного метода приближенного моделирования случайных величин на ЭВМ требуется небольшое количество операций; кроме того, количество операций не зависит от точности аппроксимации (т. е. от количества интервалов  Точность аппроксимации влияет только на размеры участка памяти, куда помещается таблица закодированных значений
Точность аппроксимации влияет только на размеры участка памяти, куда помещается таблица закодированных значений  Этим способом преобразования случайных чисел широко пользуются в практике статистического моделирования.
Этим способом преобразования случайных чисел широко пользуются в практике статистического моделирования.
Небезынтересны также способы получения случайных чисел с заданным законом распределения, основанные на использовании предельных теорем теории вероятностей. В качестве примера рассмотрим способ получения случайных чисел с нормальным законом распределения, весьма часто встречающийся при решении практических задач.
В силу центральной предельной теоремы теории вероятностей сумма большого числа одинаково распределенных независимых случайных величин при весьма общих условиях имеет приближенно нормальное распределение.
Пусть  случайные величины, имеющие равномерное распределение в интервале (0,1). Тогда
случайные величины, имеющие равномерное распределение в интервале (0,1). Тогда

оказывается случайной величиной с распределением, близким к нормальному, при больших 
Как известно, математическое ожидание (среднее значение) случайной величины

а среднее квадратическое отклонение

Поэтому математическое ожидание а суммы 

а среднее квадратическое отклонение

Процедура формирования случайных чисел с нормальным распределением, имеющим  сводится к следующему:
сводится к следующему:
1) выбираются  последовательных случайных чисел
последовательных случайных чисел 
2) вычисляется сумма 
3) определяется случайное число

имеющее приближенно нормальное распределение со средним значением, равным 0, и дисперсией —1. Как показывает опыт, для решения практических задач можно пользоваться 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ (МОНТЕ КАРЛО)
- 2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
- 3. Кратные интегралы
- 4. Требуемое количество операций
- Глава II. ПОЛУЧЕНИЕ И ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ
- 6. Получение случайных чисел с заданным законом распределения
- 7. Приближенные способы преобразования случайных чисел
- 8. Моделирование случайных векторов
- Глава III. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
- 10. Этапы формализации реальных сложных систем
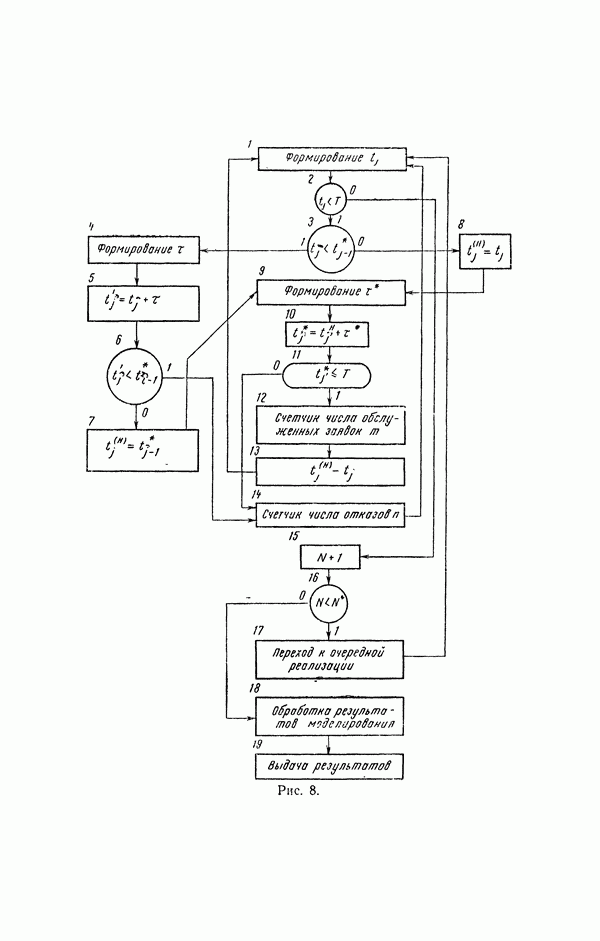
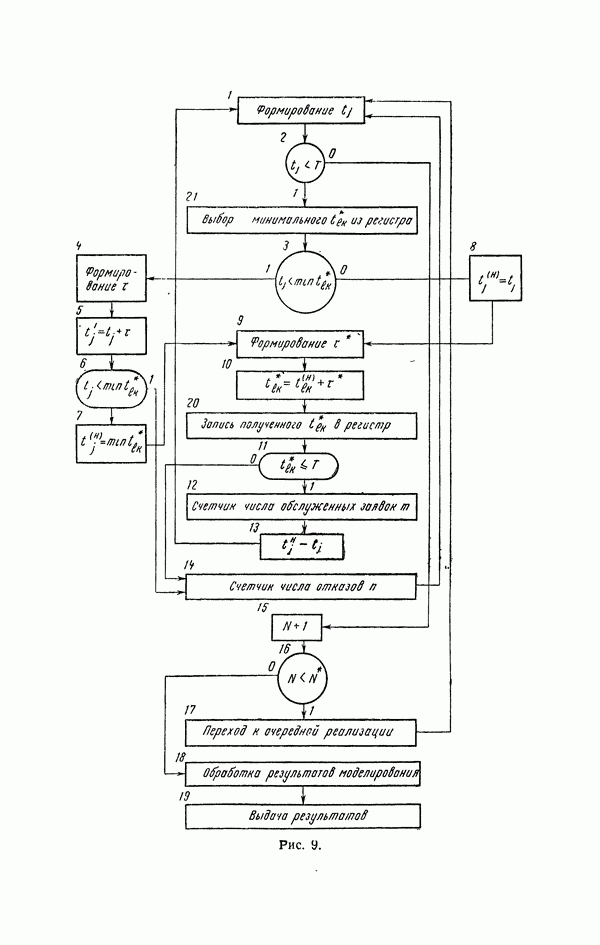
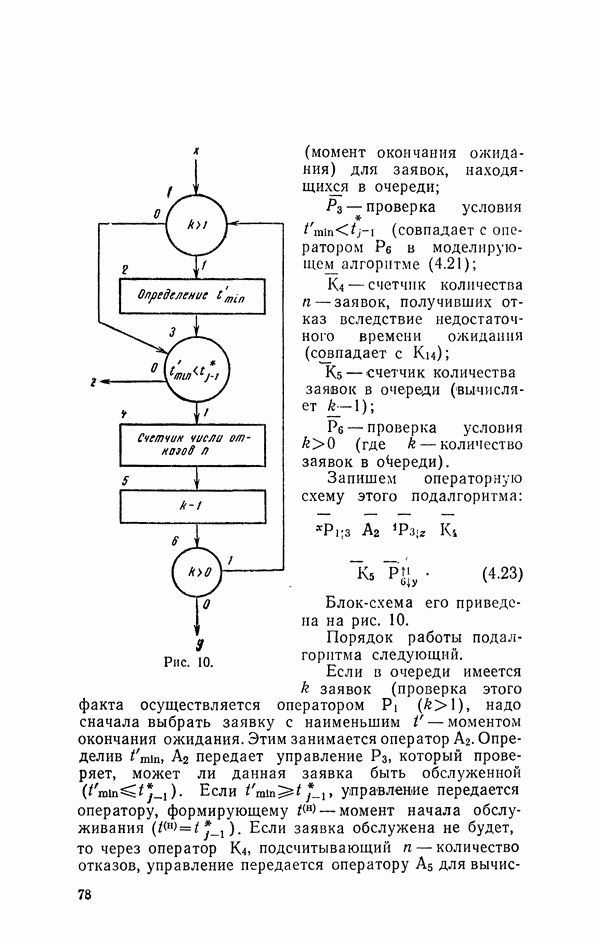
- 11. Операторная схема моделирующего алгоритма
- 12. Метод статистического моделирования как аппарат анализа сложных систем
- Глава IV. СТАТИСТИЧЕСКИЕ МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
- 13. Понятие системы массового обслуживания
- 14. Моделирование потоков заявок
- 15. Моделирование одноканальной системы массового обслуживания
- 16. Моделирование многоканальной системы
- 17. Модификаций систем массового обслуживания
- Глава V. МОДЕЛИРОВАНИЕ АВТОМОБИЛЬНОГО ДВИЖЕНИЯ
- 19. Описание потока автомобилей
- 20. Структура моделирующего алгоритма
- 21. Исходные данные и результаты моделирования