| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8. Моделирование случайных векторов
При решении задач методом статистических испытаний нередко возникает необходимость в формировании возможных значений или, как иногда говорят, реализаций случайных векторов.
Случайный вектор можно задать проекциями на оси координат, причем эти проекции являются случайными
величинами, описываемыми совместным законом распределения. В простейшем случае, когда рассматривается случайный вектор на плоскости  необходимо задать совместный закон распределения его проекций
необходимо задать совместный закон распределения его проекций  на оси X и Y соответственно.
на оси X и Y соответственно.
Предположим сначала, что двумерная случайная величина  является дискретной и ее составляющая
является дискретной и ее составляющая  принимает возможные значения
принимает возможные значения  составляющая
составляющая  — значения
— значения  причем каждой паре
причем каждой паре  соответствует вероятность
соответствует вероятность  При этих предположениях можно найти частное распределение случайной величины
При этих предположениях можно найти частное распределение случайной величины  , а именно: каждому возможному значению
, а именно: каждому возможному значению  случайной величины
случайной величины  будет соответствовать вероятность
будет соответствовать вероятность

Теперь по правилам, рассмотренным в § 6 (см. (2.8), (2.9) и др.), можно определить конкретное значение  случайной величины
случайной величины  в соответствии с распределением вероятностей (2.32). Пусть это будет
в соответствии с распределением вероятностей (2.32). Пусть это будет  Тогда из всех значений
Тогда из всех значений  выберем совокупность
выберем совокупность

которая описывает условное распределение случайной величины  при условии, что
при условии, что  . Затем по тем же правилам определим конкретное значение
. Затем по тем же правилам определим конкретное значение  (пусть оно равно
(пусть оно равно  ) случайной величины
) случайной величины  в соответствии с распределением вероятностей (2.33). Полученная пара
в соответствии с распределением вероятностей (2.33). Полученная пара  и будет первой реализацией моделируемого случайного вектора. Далее аналогичным способом определяем возможное значение
и будет первой реализацией моделируемого случайного вектора. Далее аналогичным способом определяем возможное значение  в соответствии с распределением (2.32), выбираем совокупность
в соответствии с распределением (2.32), выбираем совокупность

и находим  в соответствии с распределением вероятностей (2.34) и т. д.
в соответствии с распределением вероятностей (2.34) и т. д.
Процедура моделирования не претерпевает принципиальных изменений и в том случае, когда речь идет о моделировании непрерывного случайного вектора. В этом случае двумерная случайная величина  описывается совместной функцией плотности
описывается совместной функцией плотности  Частная
Частная
функция плотности случайной величины  может быть определена в соответствии с соотношением, аналогичным (2.32), а именно:
может быть определена в соответствии с соотношением, аналогичным (2.32), а именно:

Имея функцию плотности  можно найти случайное число
можно найти случайное число  (пусть это будет
(пусть это будет  по правилам, рассмотренным в § 7. Затем определяется условное распределение случайной величины
по правилам, рассмотренным в § 7. Затем определяется условное распределение случайной величины  при условии, что
при условии, что 

В соответствии с функцией плотиости (2.36) можно определить случайное число  (пусть это будет
(пусть это будет  Тогда пара
Тогда пара  и является искомой реализацией вектора
и является искомой реализацией вектора 
Рассматриваемый метод формирования реализаций случайных векторов в принципе обобщается на случай пространства любого числа измерений  многомерные случайные величины). Однако при больших
многомерные случайные величины). Однако при больших  объем вычислений существенно возрастает и может служить серьезным препятствием для практической работы.
объем вычислений существенно возрастает и может служить серьезным препятствием для практической работы.
Процедура формирования реализаций случайного вектора значительно упрощается и становится менее громоздкой в том случае, когда многомерная случайная 4 величина задается в рамках корреляционной теории (при помощи корреляционной матрицы).
Остановимся кратко на трехмерном случае. Пусть требуется сформировать реализации трехмерного случайного вектора  , имеющего нормальное распределение с математическими ожиданиями
, имеющего нормальное распределение с математическими ожиданиями

и корреляционной матрицей

Здесь  дисперсии случайных величин I, Л и
дисперсии случайных величин I, Л и  соответственно,
соответственно,  корреляционные моменты
корреляционные моменты  соответственно.
соответственно.
Будем предполагать, что в нашем распоряжении имеются случайные числа  имеющие одномерное нормальное распределение с математическим ожиданием
имеющие одномерное нормальное распределение с математическим ожиданием  и дисперсией
и дисперсией  Способы формирования случайных чисел, обладающих такими свойствами, мы уже рассматривали.
Способы формирования случайных чисел, обладающих такими свойствами, мы уже рассматривали.
Выберем три числа, скажем  и преобразуем их так, чтобы они имели характеристики (2.37) и (2.38).
и преобразуем их так, чтобы они имели характеристики (2.37) и (2.38).
Искомые составляющие случайного вектора  обозначим
обозначим  и представим в виде:
и представим в виде:

где  — пока неизвестные нам коэффициенты. Для вычисления коэффициентов
— пока неизвестные нам коэффициенты. Для вычисления коэффициентов  воспользуемся элементами корреляционной матрицы. По определению
воспользуемся элементами корреляционной матрицы. По определению

поэтому

Аналогично, поскольку  при
при  (случайные величины
(случайные величины  независимы между собой):
независимы между собой):

Соотношения (2.40) и 2.41) представляют собой систему уравнений относительно коэффициентов  Решив эту систему уравнений, найдем:
Решив эту систему уравнений, найдем:

Располагая коэффициентами  легко три последовательных независимых случайных числа
легко три последовательных независимых случайных числа  преобразовать в составляющие случайного вектора
преобразовать в составляющие случайного вектора  вида (2.39).
вида (2.39).
На этом мы закончим рассмотрение приемов моделирования элементарных вероятностных схем при помощи случайных чисел. Аналогичные приемы могут быть разработаны и для других случаев, встречающихся при решении практических задач.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ (МОНТЕ КАРЛО)
- 2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
- 3. Кратные интегралы
- 4. Требуемое количество операций
- Глава II. ПОЛУЧЕНИЕ И ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ
- 6. Получение случайных чисел с заданным законом распределения
- 7. Приближенные способы преобразования случайных чисел
- 8. Моделирование случайных векторов
- Глава III. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
- 10. Этапы формализации реальных сложных систем
- 11. Операторная схема моделирующего алгоритма
- 12. Метод статистического моделирования как аппарат анализа сложных систем
- Глава IV. СТАТИСТИЧЕСКИЕ МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
- 13. Понятие системы массового обслуживания
- 14. Моделирование потоков заявок
- 15. Моделирование одноканальной системы массового обслуживания
- 16. Моделирование многоканальной системы
- 17. Модификаций систем массового обслуживания
- Глава V. МОДЕЛИРОВАНИЕ АВТОМОБИЛЬНОГО ДВИЖЕНИЯ
- 19. Описание потока автомобилей
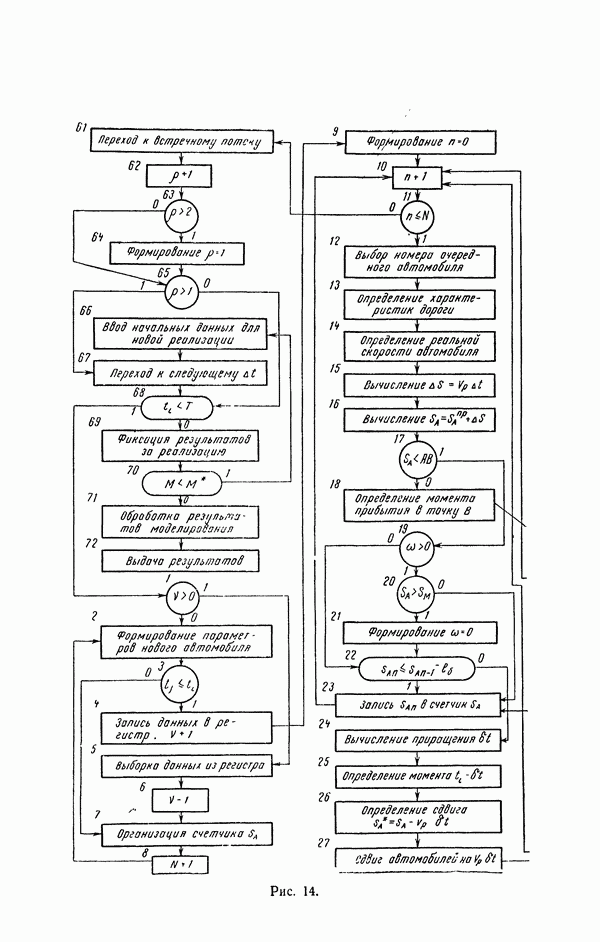
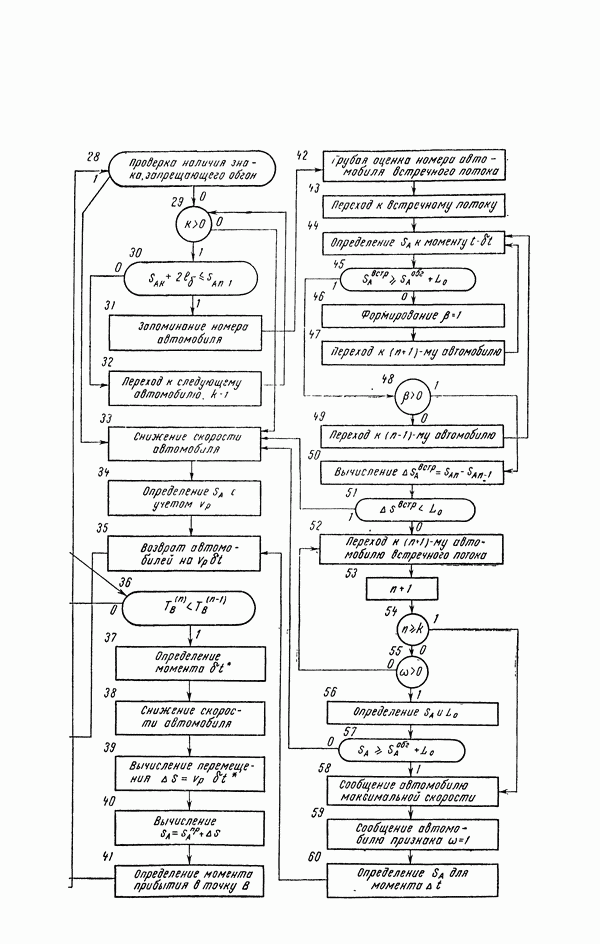
- 20. Структура моделирующего алгоритма
- 21. Исходные данные и результаты моделирования