| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
17. Модификаций систем массового обслуживания
Системы массового обслуживания как математические схемы для формального описания функционирования реальных систем крайне дифференцированы. Поэтому случаи, встречающиеся на практике, далеко не исчерпываются рассмотренными выше простейшими одноканальной и многоканальной системами. Виды этих систем столь многочисленны, что нет возможности даже кратко на всех остановиться. Теперь мы рассмотрим важнейшие виды систем массового обслуживания более общего характера, чем описанные выше; приведем соответствующие примеры.
Начнем с возможных вариантов дисциплины очереди заявок. В рассмотренных выше одноканальной и многоканальной системах массового обслуживания заявки, поступающие в систему, обслуживаются в порядке поступления. Иногда для некоторых важных в практическом отношении задач такой порядок обслуживания оказывается невыгодным. Нередки случаи, когда заявки, имеющие право  порядке очереди) на немедленное обслуживание, могут находиться в системе довольно долго
порядке очереди) на немедленное обслуживание, могут находиться в системе довольно долго  — велико) и обслуживаться после других заявок, - имеющих малое
— велико) и обслуживаться после других заявок, - имеющих малое  и поэтому быстро покидающих систему. Очевидно, что здесь мы сталкиваемся с упомянутым выше случаем целесообразности изменения порядка обслуживания, а именно: предпочтительного обслуживания заявок, ранее других покидающих систему.
и поэтому быстро покидающих систему. Очевидно, что здесь мы сталкиваемся с упомянутым выше случаем целесообразности изменения порядка обслуживания, а именно: предпочтительного обслуживания заявок, ранее других покидающих систему.
Рассмотрим несложную модификацию, позволяющую использовать алгоритм (4.21) для моделирования систем такого типа.
В момент освобождения линии  в очереди может оказаться несколько заявок. Необходимо предусмотреть специальный блок операторов (подалгоритм), занимающихся фиксацией всех
в очереди может оказаться несколько заявок. Необходимо предусмотреть специальный блок операторов (подалгоритм), занимающихся фиксацией всех  для заявок, находящихся, в очереди, и отысканием заявки, которая ранее других покидает систему.
для заявок, находящихся, в очереди, и отысканием заявки, которая ранее других покидает систему.
Для модификации алгоритма (4.21) нам требуются следующие операторы:
 -проверка условия
-проверка условия  (где
(где  — количество заявок в очереди);
— количество заявок в очереди);
 — определение
— определение  — наименьшего значения
— наименьшего значения 
(момент окончания ожидания) для заявок, находящихся в очереди;
 — проверка условия
— проверка условия
 (совпадает с оператором
(совпадает с оператором  в моделирующем алгоритме (4.21);
в моделирующем алгоритме (4.21);
 — счетчик количества
— счетчик количества  — заявок, получивших отказ вследствие недостаточного времени ожидання (совпадает с
— заявок, получивших отказ вследствие недостаточного времени ожидання (совпадает с  )
)
 — счетчик количества заявок в очереди (вычисляет
— счетчик количества заявок в очереди (вычисляет  )
)
 — проверка условия
— проверка условия  (где
(где  — количество заявок в опереди).
— количество заявок в опереди).
Запишем операторную схему этого подалгоритма:

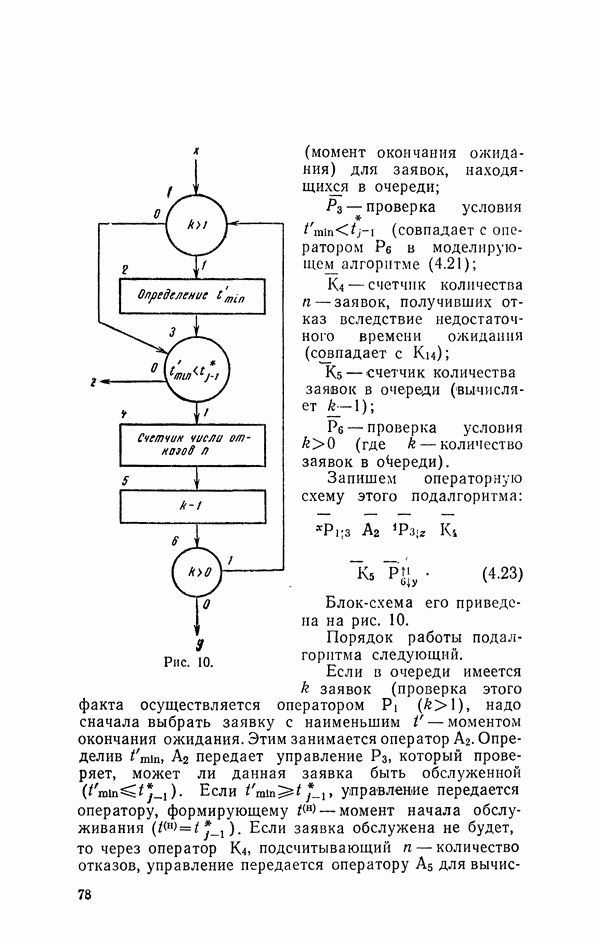
Блок-схема его приведена на рис. 10.

Рис. 10.
Порядок работы подалгоритма следующий.
Если в очереди имеется  заявок (проверка этого факта осуществляется оператором
заявок (проверка этого факта осуществляется оператором  надо сначала выбрать заявку с наименьшим
надо сначала выбрать заявку с наименьшим  — моментом окончания ожидания. Этим занимается оператор
— моментом окончания ожидания. Этим занимается оператор  Определив
Определив  передает управление
передает управление  который проверяет, может ли данная заявка быть обслуженной
который проверяет, может ли данная заявка быть обслуженной  Если
Если  управление передается оператору, формирующему
управление передается оператору, формирующему  — момент начала обслуживания
— момент начала обслуживания  Если заявка обслужена не будет, то через оператор
Если заявка обслужена не будет, то через оператор  подсчитывающий
подсчитывающий  — количество отказов, управление передается оператору
— количество отказов, управление передается оператору  для вычисления
для вычисления
количества заявок в очереди  и затем оператору
и затем оператору  для проверки неравенства
для проверки неравенства  Если
Если  (существует очередь заявок), управление передается снова оператору
(существует очередь заявок), управление передается снова оператору  и затем
и затем  для перегруппировки заявок в очереди (определения нового
для перегруппировки заявок в очереди (определения нового  Если неравенство
Если неравенство  не выполнено (нет очереди заявок), управление передается оператору, формирующему
не выполнено (нет очереди заявок), управление передается оператору, формирующему  момент поступления новой заявки.
момент поступления новой заявки.
Эта модификация моделирующего алгоритма позволяет кроме обычных результатов получить дополнительные характеристики моделируемого процесса, такие, как среднюю длину очереди и среднее время ожидания. Это нетрудно сделать, выводя на печать величину  для каждого момента изменения его значения (поступления новой заявки, взятие очередной заявки на обслуживание или получения отказа), а также моменты
для каждого момента изменения его значения (поступления новой заявки, взятие очередной заявки на обслуживание или получения отказа), а также моменты  окончания ожидания для всех заявок в очереди.
окончания ожидания для всех заявок в очереди.
В качестве примера других возможных вариантов дисциплины очереди рассмотрим обслуживание в случайном порядке в соответствии с заданными вероятностями.
Пусть время пребывания заявки в системе ограничено как в алгоритме (4.21), а заявки принимаются к обслуживанию в соответствии с вероятностями  задаваемыми заранее или вычисляемыми в процессе моделирования.
задаваемыми заранее или вычисляемыми в процессе моделирования.
Приводим необходимые операторы:
 — проверка условия
— проверка условия 
 — счетчик числа отказов
— счетчик числа отказов 
 — запоминание (запись в регистр) заявки, удовлетворяющей условию; проверяемому оператором
— запоминание (запись в регистр) заявки, удовлетворяющей условию; проверяемому оператором 
 — счетчик количества
— счетчик количества  — заявок в регистре (операция
— заявок в регистре (операция  )
)
 — счетчик количества
— счетчик количества  — заявок в очереди
— заявок в очереди 
 — проверка наличия заявок в очереди
— проверка наличия заявок в очереди 
 — проверка наличия заявок в регистре
— проверка наличия заявок в регистре 
 — выбор заявки в соответствии с заданными вероятностями;
— выбор заявки в соответствии с заданными вероятностями;
 — формирование
— формирование  — момента начала обслуживания для выбранной заявки
— момента начала обслуживания для выбранной заявки 
Операторную схему подалгаритма можно записать так:

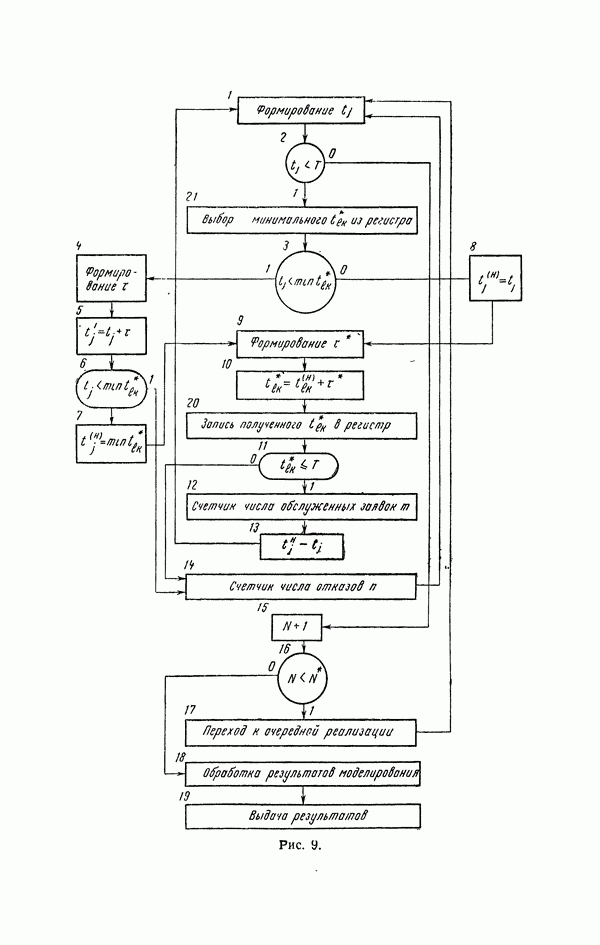
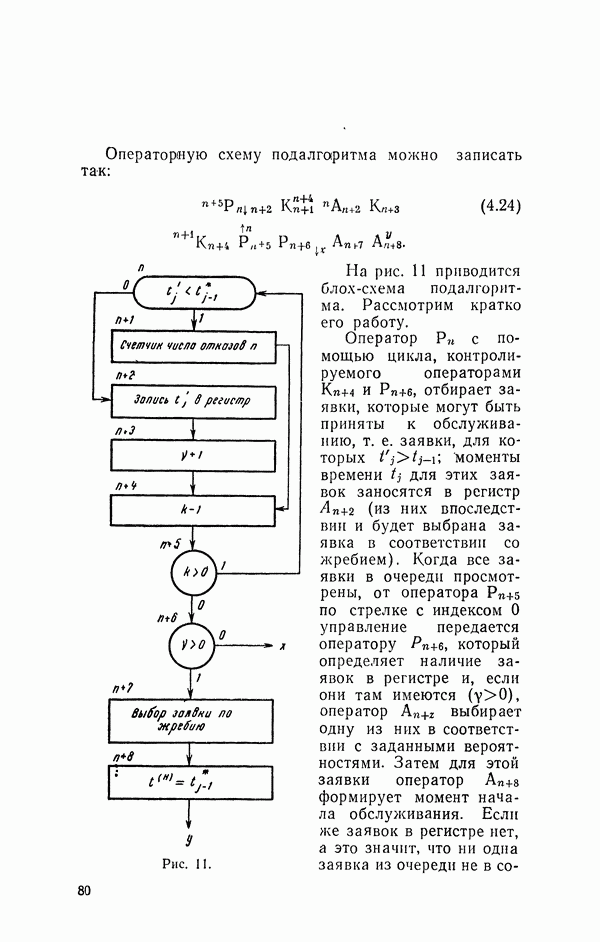
На рис. 11 приводится блох - схема подалгоритма. Рассмотрим кратко его работу.

Рис. 11.
Оператор  с помощью цикла, контролируемого операторами
с помощью цикла, контролируемого операторами  отбирает заявки, которые могут быть приняты к обслуживанию, т. е. заявки, для которых
отбирает заявки, которые могут быть приняты к обслуживанию, т. е. заявки, для которых  моменты времени
моменты времени  для этих заявок заносятся в регистр
для этих заявок заносятся в регистр  (из них впоследствии и будет выбрана заявка в соответствии со жребием). Когда все заявки в очереди просмотрены, от оператора
(из них впоследствии и будет выбрана заявка в соответствии со жребием). Когда все заявки в очереди просмотрены, от оператора  по стрелке с индексом О управление передается оператору
по стрелке с индексом О управление передается оператору  который определяет наличие заявок в регистре и, если они там имеются
который определяет наличие заявок в регистре и, если они там имеются  оператор
оператор  выбирает одну из них в соответствии с заданными вероятностями. Затем для этой заявки оператор
выбирает одну из них в соответствии с заданными вероятностями. Затем для этой заявки оператор  формирует момент начала обслуживания. Если же заявок в регистре нет, а это значит, что ни одна заявка из очереди не в
формирует момент начала обслуживания. Если же заявок в регистре нет, а это значит, что ни одна заявка из очереди не в
состоянии дождаться момента освобождения канала и, следовательно, все они получили отказ (что было зафиксировано оператором  тогда управление от оператора
тогда управление от оператора  по стрелке с индексом 0 передается оператору, формирующему новую заявку.
по стрелке с индексом 0 передается оператору, формирующему новую заявку.
Приведенная блок - схема подалгоритма может быть попользована для моделирования простейшего случая обслуживания с преимуществом, а именно для выбора заявки в соответствии с заданным коэффициентом преимущества.
Действительно, если заменить оператор  (выбор заявки по жребию) оператором — выбор заявки в соответствии с коэффициентом преимущества, мы и получим искомый алгоритм.
(выбор заявки по жребию) оператором — выбор заявки в соответствии с коэффициентом преимущества, мы и получим искомый алгоритм.
Переходя к рассмотрению дисциплины очереди обслуживающих каналов многоканальной системы массового обслуживания, остановимся на алгоритме, моделирующем выбор канала в соответствии с заданным правилом.
Для этого нам потребуются следующие операторы:
 — проверка условия
— проверка условия  где
где  — текущее,
— текущее,  максимальное значение номера обслуживающего канала;
максимальное значение номера обслуживающего канала;
 — счетчик числа каналов (реализует операцию
— счетчик числа каналов (реализует операцию  )
)
 — проверка условия
— проверка условия  где
где  момент поступления очередной заявки,
момент поступления очередной заявки,  момент освобождения
момент освобождения  канала;
канала;
 — запоминание (занесение в регистр)
— запоминание (занесение в регистр)  которых не справедливо условие, проверяемое оператором
которых не справедливо условие, проверяемое оператором 
 - счетчик количества свободных каналов в регистре (реализует операцию
- счетчик количества свободных каналов в регистре (реализует операцию  где
где  количество свободных каналов);
количество свободных каналов);
 — проверка условия
— проверка условия  ( т. е. имеются ли свободные каналы в регистре);
( т. е. имеются ли свободные каналы в регистре);
 — реализация заданного правила выбора канала для обслуживания.
— реализация заданного правила выбора канала для обслуживания.
Операторная схема подалгоритма имеет вид:

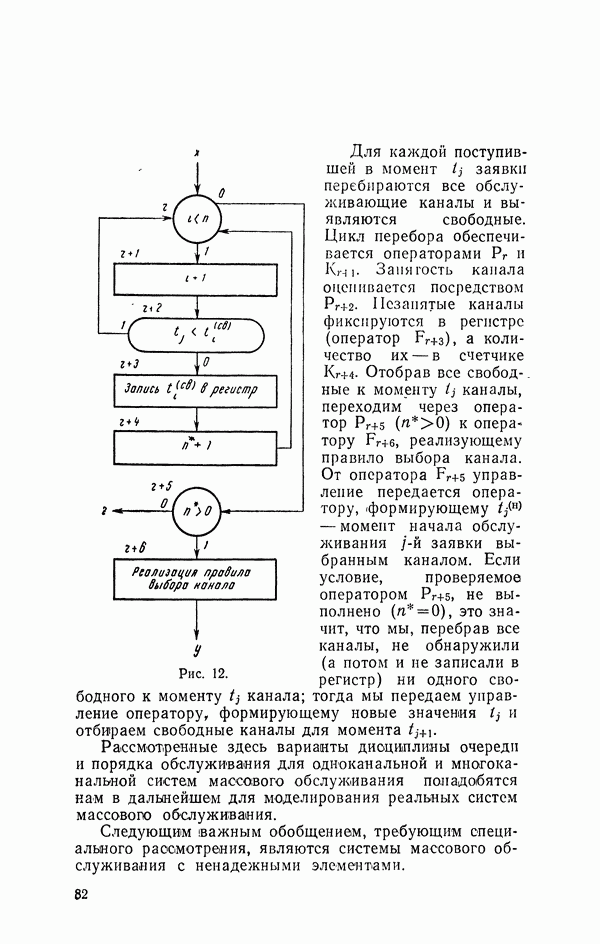
Блок - схема приведена на рис. 12.
Подалгорит,м работает следующим образом.

Рис. 12.
Для каждой поступившей в момент  заявки перебираются все обслуживающие каналы и выявляются свободные. Цикл перебора обеспечивается операторами
заявки перебираются все обслуживающие каналы и выявляются свободные. Цикл перебора обеспечивается операторами  Занятость канала оценивается посредством
Занятость канала оценивается посредством  Незанятые каналы фиксируются в регистре (оператор
Незанятые каналы фиксируются в регистре (оператор  количество их — в счетчике
количество их — в счетчике  Отобрав все свобод-,
Отобрав все свобод-,  к моменту
к моменту  каналы, переходим через оператор
каналы, переходим через оператор  к оператору
к оператору  реализующему правило выбора канала. От оператора
реализующему правило выбора канала. От оператора  управление передается оператору, формирующему — момент начала обслуживания
управление передается оператору, формирующему — момент начала обслуживания  заявки выбранным каналом. Если условие, проверяемое оператором
заявки выбранным каналом. Если условие, проверяемое оператором  не выполнено
не выполнено  это значит, что мы, перебрав все каналы, не обнаружили (а потом и не записали в регистр) ни одного свободного к моменту
это значит, что мы, перебрав все каналы, не обнаружили (а потом и не записали в регистр) ни одного свободного к моменту  канала; тогда мы передаем управление оператору, формирующему новые значения
канала; тогда мы передаем управление оператору, формирующему новые значения  и отбираем свободные каналы для момента
и отбираем свободные каналы для момента 
Рассмотренные здесь варианты дисциплины очереди и порядка обслуживания для одноканальной и многоканальной систем массового обслуживания понадобятся нам в дальнейшем для моделирования реальных систем массового обслуживания.
Следующим важным обобщением, требующим специального рассмотрения, являются системы массового обслуживания с ненадежными элементами.
Во многих практических задачах системы массового обслуживания рассматриваются как системы с ненадежными элементами. В общем случае это означает, что в некоторый момент времени  в работе обслуживающего канала происходит отказ (сбой); канал может быть отремонтирован за время
в работе обслуживающего канала происходит отказ (сбой); канал может быть отремонтирован за время  и снова приступить к обслуживанию в момент времени
и снова приступить к обслуживанию в момент времени 
Надежность канала задается функцией распределения интервала безотказной работы  равной вероятности того, что
равной вероятности того, что 

а  (время ремонта) - как случайная величина с задан ным законом распределения.
(время ремонта) - как случайная величина с задан ным законом распределения.
Можно интерпретировать сбой и ремонт канала как обслуживание фиктивной заявки с моментом начала обслуживания  длительностью обслуживания и главенствующим коэффициентом преимущества. Весь период ремонта канал можно считать фиктивно занятым. Обычно принимаются два предположения относительно судьбы заявки, находящейся на обслуживании в момент сбоя; либо заявка получает отказ и уходит из системы, либо ее обслуживание может быть продолжено после устранения последствий сбоя (после ремонта).
длительностью обслуживания и главенствующим коэффициентом преимущества. Весь период ремонта канал можно считать фиктивно занятым. Обычно принимаются два предположения относительно судьбы заявки, находящейся на обслуживании в момент сбоя; либо заявка получает отказ и уходит из системы, либо ее обслуживание может быть продолжено после устранения последствий сбоя (после ремонта).
Рассмотрим принципы моделирования систем с ненадежными элементами на примере одноканальной системы (4.21).
-Пусть мы имеем одноканальную систему. Дополним ее описание следующими свойствами: в моменты времени  заданные законом распределения
заданные законом распределения  канал выходит из строя; ремонт его продолжается случайное время
канал выходит из строя; ремонт его продолжается случайное время  заданное законом распределения
заданное законом распределения  заявка, при обслуживании которой наступил сбой, получает отказ.
заявка, при обслуживании которой наступил сбой, получает отказ.
Воспользуемся следующими операторами:
 — проверка условия
— проверка условия 
 — формирование случайного числа
— формирование случайного числа  в соответствии с функцией распределения (4.26);
в соответствии с функцией распределения (4.26);
 — выбор
— выбор  из памяти;
из памяти;
 — проверка условия
— проверка условия 
 — запись
— запись  в память, формирование
в память, формирование 
 — формирование
— формирование 
 — проверка условия
— проверка условия 
 — формирование случайного значения
— формирование случайного значения  времени ремонта обслуживающего канала;
времени ремонта обслуживающего канала;
 определение момента — готовности капала к обслуживанию после ремонта;
определение момента — готовности капала к обслуживанию после ремонта;
 — проверка условия
— проверка условия  (возможности обслужить заявку после ремонта).
(возможности обслужить заявку после ремонта).
Операторная схема подалгоритма учета надежности  может быть представлена в виде:
может быть представлена в виде:

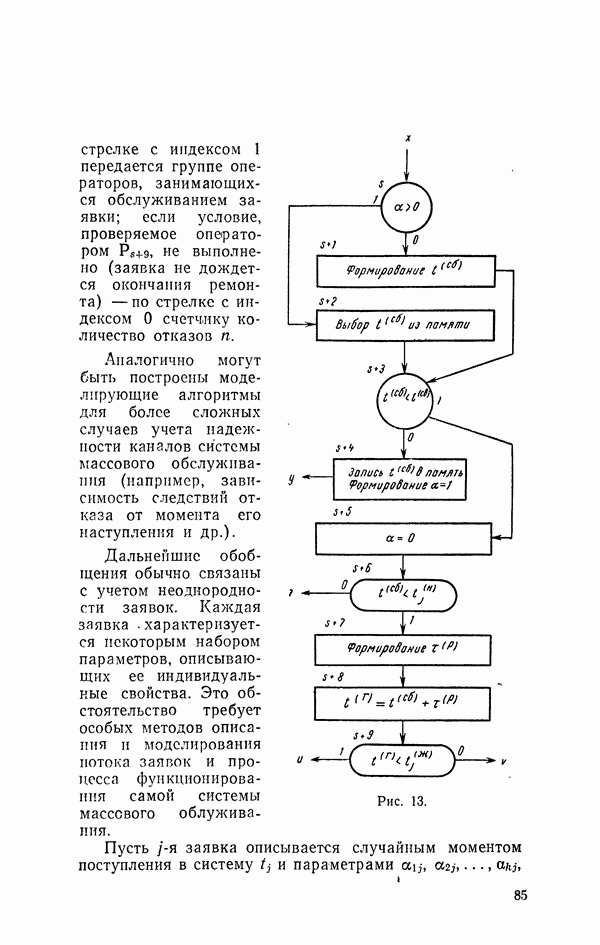
Блок-схема подалгоритма представлена на рис. 13. Подалгоритм работает следующим образом.
Оператор  проверяет условие
проверяет условие  Если
Если  это свидетельствует, что значение
это свидетельствует, что значение  уже сформировано и записано в память; управление передается оператору
уже сформировано и записано в память; управление передается оператору  для извлечения
для извлечения  из памяти. В противном случае
из памяти. В противном случае  оператор
оператор  формирует значение
формирует значение  Оператор
Оператор  проверяет неравенство
проверяет неравенство  Если это неравенство не выполнено, т. е. сбой произошел после окончания обслуживания, то заявка может быть обслужена. В этом случае значение
Если это неравенство не выполнено, т. е. сбой произошел после окончания обслуживания, то заявка может быть обслужена. В этом случае значение  следует записать в память, сформировав признак
следует записать в память, сформировав признак  (свидетельствующий о наличии
(свидетельствующий о наличии  в памяти). Если неравенство
в памяти). Если неравенство  выполнено, вопрос о возможности обслужить заявку будет рассматриваться особо. Значение
выполнено, вопрос о возможности обслужить заявку будет рассматриваться особо. Значение  уже не понадобится нам
уже не понадобится нам  рассмотрении последующих заявок, поэтому управление но стрелке с индексом 1 передается оператору
рассмотрении последующих заявок, поэтому управление но стрелке с индексом 1 передается оператору  для формирования
для формирования  Если неравенство
Если неравенство  проверяемое оператором
проверяемое оператором  не выполнено, т. е.
не выполнено, т. е.  (сбой произошел после начала обслуживания) - заявка получает отказ (управление по стрелке с индексом 0 передается оператору, фиксирующему количество отказов). Если условие, проверяемое оператором
(сбой произошел после начала обслуживания) - заявка получает отказ (управление по стрелке с индексом 0 передается оператору, фиксирующему количество отказов). Если условие, проверяемое оператором  выполнено —
выполнено —  (сбой произошел до начала обслуживания), вопрос о возможности обслужить заявку нельзя решить, не зная
(сбой произошел до начала обслуживания), вопрос о возможности обслужить заявку нельзя решить, не зная  -времени ремонта. Оператор
-времени ремонта. Оператор  формирует и затем оператор
формирует и затем оператор  вычисляет
вычисляет  (момент окончания ремонта). Теперь судьба заявки может быть выяснена. Если условие, проверяемое оператором
(момент окончания ремонта). Теперь судьба заявки может быть выяснена. Если условие, проверяемое оператором  выполнено —
выполнено —  (ремонт окончится раньше, чем истечет время ожидания), управление по
(ремонт окончится раньше, чем истечет время ожидания), управление по
стрелке с индексом 1 передается группе операторов, занимающихся обслуживанием заявки; если условие, проверяемое оператором  не выполнено (заявка не дождется окончания ремонта) — по стрелке с индексом 0 счетчику количество отказов
не выполнено (заявка не дождется окончания ремонта) — по стрелке с индексом 0 счетчику количество отказов 
Аналогично могут быть построены моделирующие алгоритмы для более сложных случаев учета надежности каналов системы массового обслуживания (например, зависимость следствий отказа от момента его наступления и Др.).
Дальнейшие обобщения обычно связаны с учетом неоднородности заявок. Каждая заявка характеризуется некоторым набором параметров, описывающих ее индивидуальные свойства. Это обстоятельство требует особых методов описания и моделирования потока заявок и процесса функционирования самой системы массового облуживания.

Рис. 13.
Пусть  заявка описывается случайным моментом поступления в систему
заявка описывается случайным моментом поступления в систему  и параметрами
и параметрами 
принимающими случайные значения. Математической схемой для описания потока неоднородных заявок может служить схема потока случайных векторов. В общем веде эта схема сложна и громоздка с точки зрения реализации на ЭВМ. При решении практических задач стремятся поток моментов поступления заявок представить как поток однородных событий, а случайные параметры описать соответствующими условными (или безусловными, колда параметры и поток моментов независимы) распределениями вероятностей. При этом мы приходим к необходимости формировать на ЭВМ реализации многомерных случайных векторов (см. главу II). Объем вычислений уменьшается, если составляющие случайного вектора независимы (например, поток с ограниченным последействием).
Неоднородность заявок оказывает влияние и на процесс «их обслуживания. Наиболее распространены случаи, когда характеристики обслуживания, такие, как время ожидания обслуживания  время занятости канала (длительность обслуживания)
время занятости канала (длительность обслуживания)  и т. д., являются функциями параметров заявки
и т. д., являются функциями параметров заявки  Это обстоятельство учитывается при моделировании: к операторам моделирующего алгоритма добавляются соотношения для расчета
Это обстоятельство учитывается при моделировании: к операторам моделирующего алгоритма добавляются соотношения для расчета  и т.
и т.
Наконец, на практике встречаются системы, обладающие специальными комплексами управления, которые по заданным параметрам заявки и известньим характеристикам состояний системы обслуживания вырабатывают команды, определяющие порядок обслуживания и значения характеристик обслуживания. Моделирование таких систем на ЭВМ проводится с использованием рассмотренных выше методов, но с дополнениями к моделирующему алгоритму, имитирующими работу комплекса управления. Обычно имитация сводится к воспроизведению на ЭВМ некоторых формально описанных алгоритмов, хотя бы приближенно представляющих работу комплекса управления.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ (МОНТЕ КАРЛО)
- 2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
- 3. Кратные интегралы
- 4. Требуемое количество операций
- Глава II. ПОЛУЧЕНИЕ И ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ
- 6. Получение случайных чисел с заданным законом распределения
- 7. Приближенные способы преобразования случайных чисел
- 8. Моделирование случайных векторов
- Глава III. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
- 10. Этапы формализации реальных сложных систем
- 11. Операторная схема моделирующего алгоритма
- 12. Метод статистического моделирования как аппарат анализа сложных систем
- Глава IV. СТАТИСТИЧЕСКИЕ МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
- 13. Понятие системы массового обслуживания
- 14. Моделирование потоков заявок
- 15. Моделирование одноканальной системы массового обслуживания
- 16. Моделирование многоканальной системы
- 17. Модификаций систем массового обслуживания
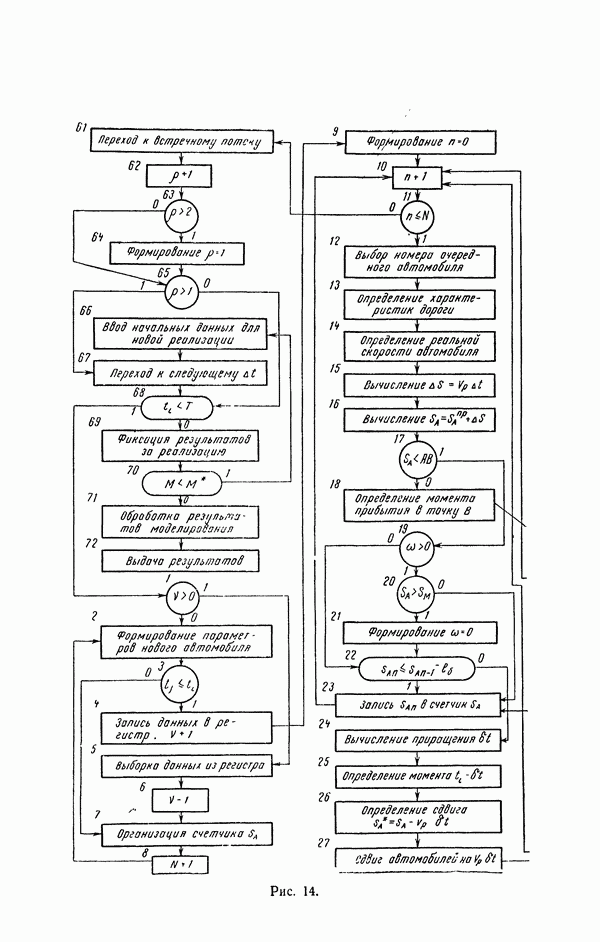
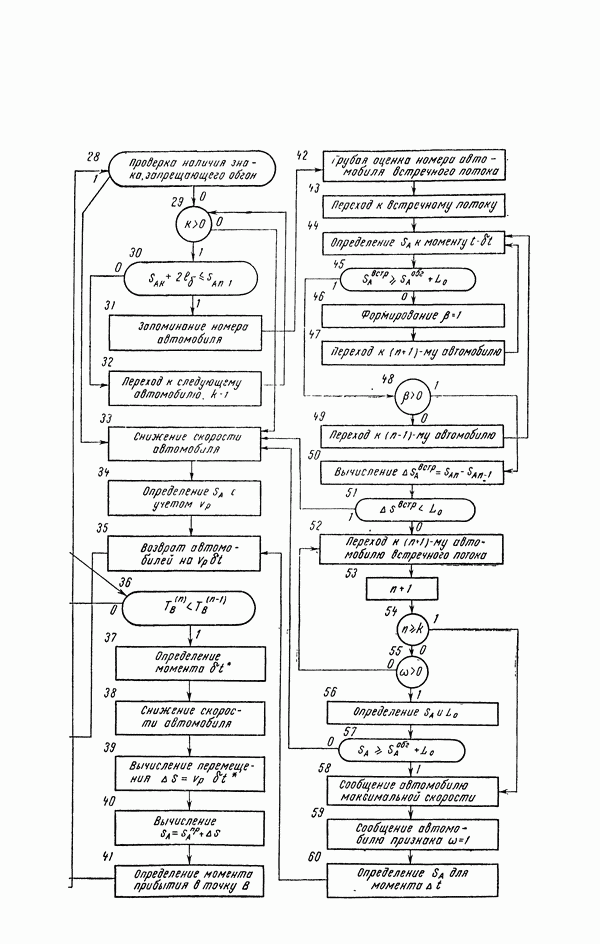
- Глава V. МОДЕЛИРОВАНИЕ АВТОМОБИЛЬНОГО ДВИЖЕНИЯ
- 19. Описание потока автомобилей
- 20. Структура моделирующего алгоритма
- 21. Исходные данные и результаты моделирования