| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
В дальнейшем мы будем различать дискретные и непрерывные случайные величины. Дискретная случайная величина  может принимать лишь конечное или счетное множество возможных значений
может принимать лишь конечное или счетное множество возможных значений  Каждому
Каждому
возможному значению  ставится в соответствие его вероятность
ставится в соответствие его вероятность  Зависимость вида
Зависимость вида

будем называть законом распределения дискретной случайной величины. При исследовании дискретных случайных величин пользуются также функцией распределения  которая при каждом
которая при каждом  равна вероятности того, что
равна вероятности того, что 

Если известен закон распределения  всегда можно определить функцию распределения
всегда можно определить функцию распределения

и, наоборот, по заданной функции распределения  можно найти закон распределения
можно найти закон распределения

Кроме дискретных случайных величин рассматриваются случайные величины, возможные значения которых сплошь заполняют соответствующие интервалы на числовой оси. Такая случайная величина характеризуется функцией распределения, которая определяется также, как и для дискретных случайных величин; при каждом  функция распределения
функция распределения

Во многих случаях функция распределения  оказывается дифференцируемой. Если существует производная
оказывается дифференцируемой. Если существует производная

случайная величина  называется непрерывной, а функция
называется непрерывной, а функция  -функцией плотности вероятностей случайной величины
-функцией плотности вероятностей случайной величины  Очевидно, что
Очевидно, что

Рассмотрим случайную величину возможные значения которой  принадлежат некоторому интервалу на оси
принадлежат некоторому интервалу на оси  Закон распределения этой случайной величины задан функцией плотности
Закон распределения этой случайной величины задан функцией плотности  Вычислим вероятность попадания случайной величины внутрь полуинтервала
Вычислим вероятность попадания случайной величины внутрь полуинтервала  целиком лежащего в вышеуказанном интервале на оси ОХ.
целиком лежащего в вышеуказанном интервале на оси ОХ.
Из теории вероятностей известно (см. [5]), что

Для решения этой задачи воспользуемся методом статистических испытаний.
Легко видеть, что в данном случае применима уже изложенная нами процедура вычисления интеграла вида (1.9). Однако мы рассмотрим другой вариант метода статистических испытаний. Предположим, что в нашем распоряжении имеются случайные числа  закон распределения которых описывается функцией плотности
закон распределения которых описывается функцией плотности  Поскольку случайные числа
Поскольку случайные числа  можно рассматривать как возможные значения случайной величины искомая вероятность
можно рассматривать как возможные значения случайной величины искомая вероятность  приближенно (при достаточно большом числе испытаний
приближенно (при достаточно большом числе испытаний  равна частоте попадания случайных чисел
равна частоте попадания случайных чисел  в полуинтервал
в полуинтервал 

где  — количество случайных чисел, удовлетворяющих неравенству
— количество случайных чисел, удовлетворяющих неравенству

при N испытаниях.
Другими словами, в условиях данной задачи

Процедура вычисления интеграла на ЭВМ следующая:
1. Из множества случайных чисел с законом распределения  выбираем значение
выбираем значение 
 сравниваем с граничными значениями полуинтервала
сравниваем с граничными значениями полуинтервала  выполнение неравенства
выполнение неравенства  отмечаем признаком
отмечаем признаком  невыполнение
невыполнение 
3. Полученное значение признака со прибавляем к количеству случайных чисел, попавших внутрь полуинтервала 
4. К содержимому счетчика количества испытаний N прибавляется единица.
5. Управление передается снова первой операции.
Проведя N таких испытаний, вычисляем значение частоты 
Нетрудно заметить, что рассмотренный второй вариант подхода к вычислению интеграла

существенным образом отличается от первого варианта (см. стр. 14) подхода. Так, в первом варианте для реализации каждого испытания были необходимы два случайных числа  Кроме того, требовалось вычисление подынтегральной функции для каждого значения
Кроме того, требовалось вычисление подынтегральной функции для каждого значения  случайной величины что, вообще говоря, может быть связано со значительным объемом вычислений. С другой стороны, первый способ является более общим случаем вычисления интеграла; этот способ пригоден для подынтегральных функций весьма широкого класса, тогда как второй способ предполагает, что подынтегральная функция является функцией плотности некоторой случайной величины, что накладывает на нее определенные ограничения. Первый способ оперирует с равномерно распределенной случайной величиной, которую легко получить на ЭВМ, тогда как рассмотренный здесь требует специального преобразования равномерного распределения в заданное.
случайной величины что, вообще говоря, может быть связано со значительным объемом вычислений. С другой стороны, первый способ является более общим случаем вычисления интеграла; этот способ пригоден для подынтегральных функций весьма широкого класса, тогда как второй способ предполагает, что подынтегральная функция является функцией плотности некоторой случайной величины, что накладывает на нее определенные ограничения. Первый способ оперирует с равномерно распределенной случайной величиной, которую легко получить на ЭВМ, тогда как рассмотренный здесь требует специального преобразования равномерного распределения в заданное.
Перечисленные отличия разграничивают классы задач, которые удобно решать тем или другим способом. Так, первым способом широко пользуются для вычисления многократных интегралов, в то время как второй способ находит применение при моделировании сложных систем методом статистических испытаний.
Перейдем к рассмотрению еще одной разновидности применения метода статистических испытаний для вычисления интегралов.
Пусть  — случайная величина, возможные значения которой принадлежат отрезку
— случайная величина, возможные значения которой принадлежат отрезку  -функция плотности этой случайной величины. Рассмотрим непрерывную функцию
-функция плотности этой случайной величины. Рассмотрим непрерывную функцию  Из теории вероятностей известно (см. [5]), что среднее значение, или математическое ожидание функции
Из теории вероятностей известно (см. [5]), что среднее значение, или математическое ожидание функции  равно
равно

Воспользуемся методом статистических испытаний для вычисления интегралов вида (1.13). Из совокупности возможных значений  случайной величины
случайной величины  выберем последовательность
выберем последовательность  и вычислим значения
и вычислим значения  причем
причем  не принадлежащие отрезку
не принадлежащие отрезку  в расчет не принимаются. При достаточно больших N среднее арифметическое весьма близко к математическому ожиданию случайной величины. Поэтому в качестве приближенного значения для интеграла (1.13) может быть взято среднее арифметическое
в расчет не принимаются. При достаточно больших N среднее арифметическое весьма близко к математическому ожиданию случайной величины. Поэтому в качестве приближенного значения для интеграла (1.13) может быть взято среднее арифметическое

Как осуществить это практически? Пусть перед нами стоит задача вычислить

Выберем некоторый закон распределения  для которого имеется удобный способ получения случайных чисел и областью определения которого является интервал
для которого имеется удобный способ получения случайных чисел и областью определения которого является интервал  Преобразуем подынтегральную функцию следующим образом:
Преобразуем подынтегральную функцию следующим образом:

Если теперь обозначить

то интеграл примет вид

и может быть вычислен при помощи метода статистических испытаний.
В частном случае, если а и  конечны или их можно считать конечными приближенно, в качестве
конечны или их можно считать конечными приближенно, в качестве  целесообразно выбрать равномерный закон распределения.
целесообразно выбрать равномерный закон распределения.
Как известно (см. [5]), плотность вероятности равномерного закона распределения в интервале  равна:
равна:

Подставим в интеграл (1.16) значение  из формулы (1.19)
из формулы (1.19)

и рассмотрим процедуру вычисления, описанную выше, для общего случая в связи с равенством (1.14).
Из множества равномерно распределенных случайных чисел выбирается  Для каждого значения
Для каждого значения  вычисляется
вычисляется  затем вычисляется среднее значение
затем вычисляется среднее значение

функции  в интервале
в интервале  Таким образом, величина интеграла (1.20) может быть представлена следующей формулой
Таким образом, величина интеграла (1.20) может быть представлена следующей формулой

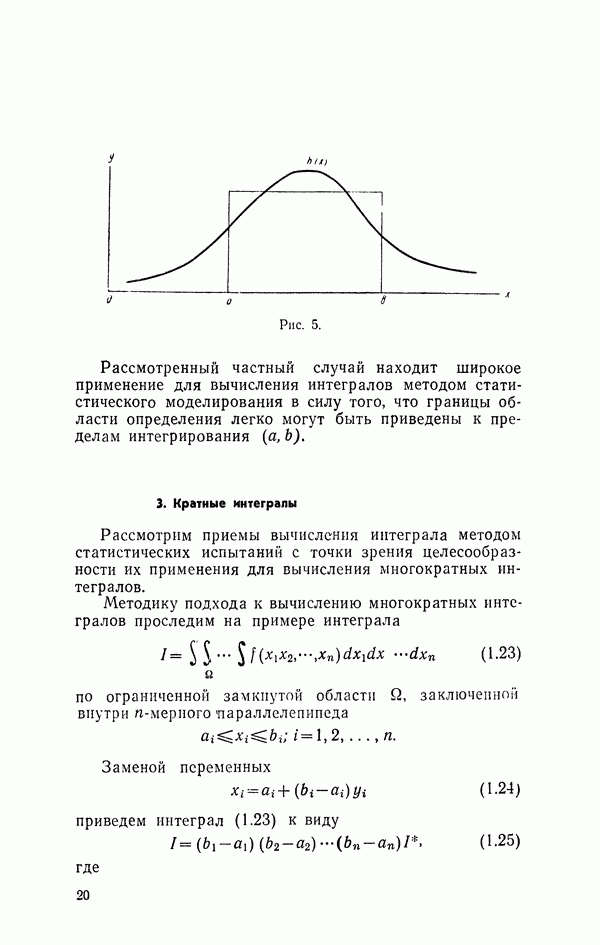
На рис. 5 видно, что площадь под кривой заменяется площадью прямоугольника с основанием  и высотой, равной среднему значению функции
и высотой, равной среднему значению функции  на отрезке
на отрезке 

Рис. 5.
Рассмотренный частный случай находит широкое применение для вычисления интегралов методом статистического моделирования в силу того, что границы области определения легко могут быть приведены к пределам интегрирования 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ (МОНТЕ КАРЛО)
- 2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
- 3. Кратные интегралы
- 4. Требуемое количество операций
- Глава II. ПОЛУЧЕНИЕ И ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ
- 6. Получение случайных чисел с заданным законом распределения
- 7. Приближенные способы преобразования случайных чисел
- 8. Моделирование случайных векторов
- Глава III. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
- 10. Этапы формализации реальных сложных систем
- 11. Операторная схема моделирующего алгоритма
- 12. Метод статистического моделирования как аппарат анализа сложных систем
- Глава IV. СТАТИСТИЧЕСКИЕ МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
- 13. Понятие системы массового обслуживания
- 14. Моделирование потоков заявок
- 15. Моделирование одноканальной системы массового обслуживания
- 16. Моделирование многоканальной системы
- 17. Модификаций систем массового обслуживания
- Глава V. МОДЕЛИРОВАНИЕ АВТОМОБИЛЬНОГО ДВИЖЕНИЯ
- 19. Описание потока автомобилей
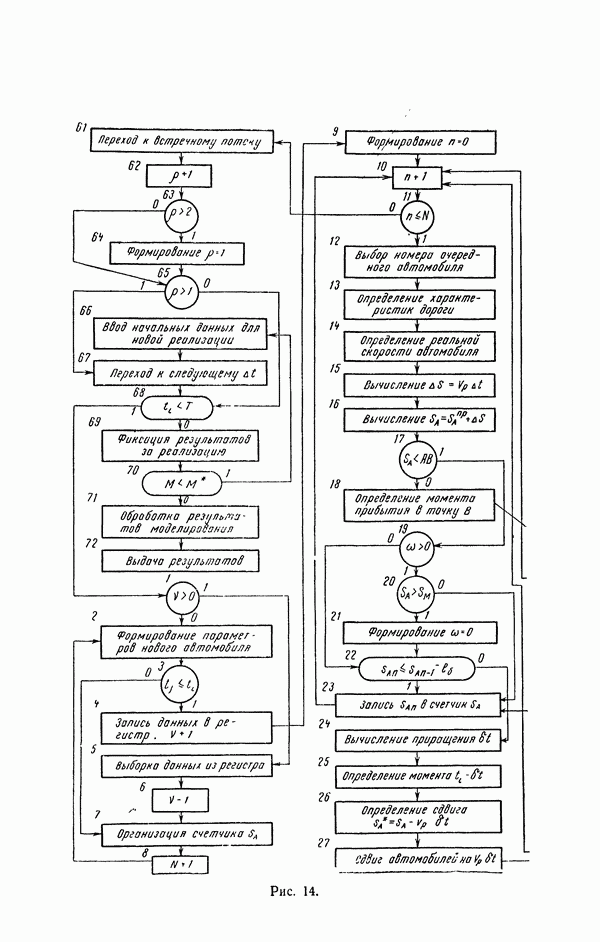
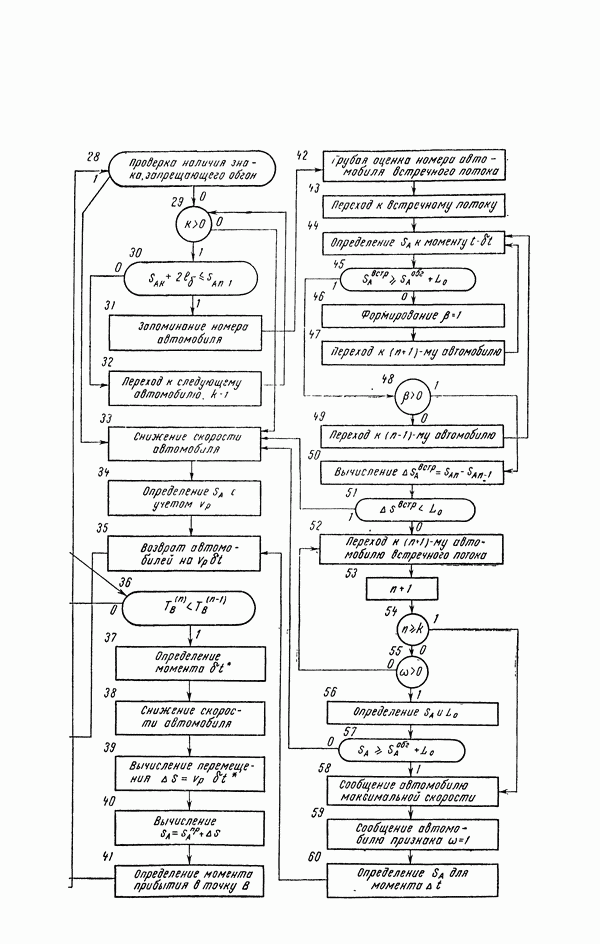
- 20. Структура моделирующего алгоритма
- 21. Исходные данные и результаты моделирования