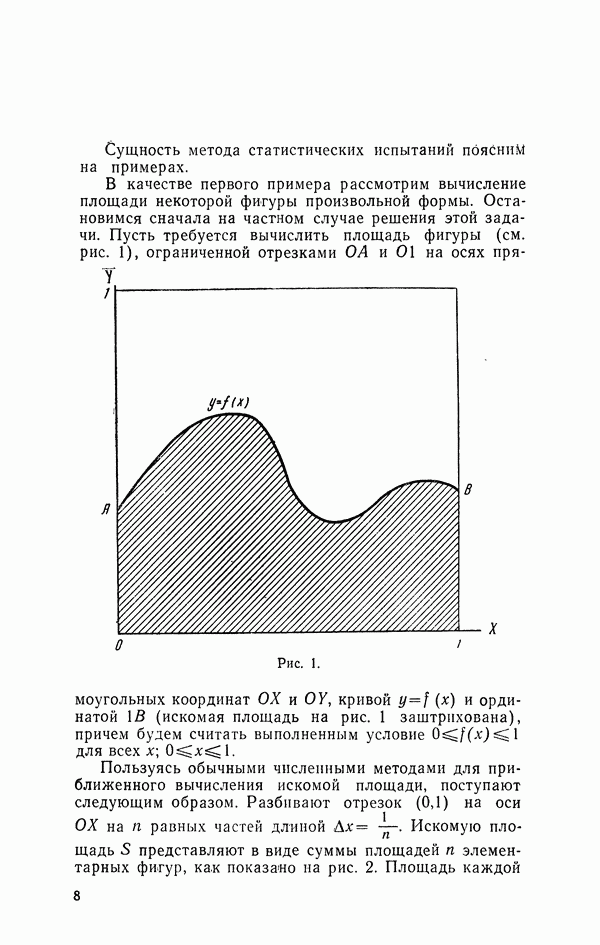
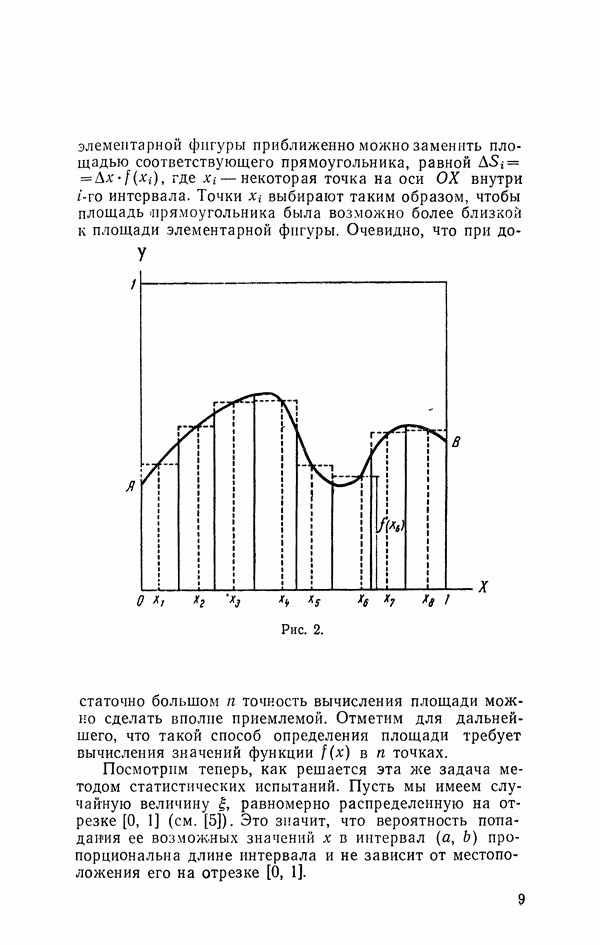
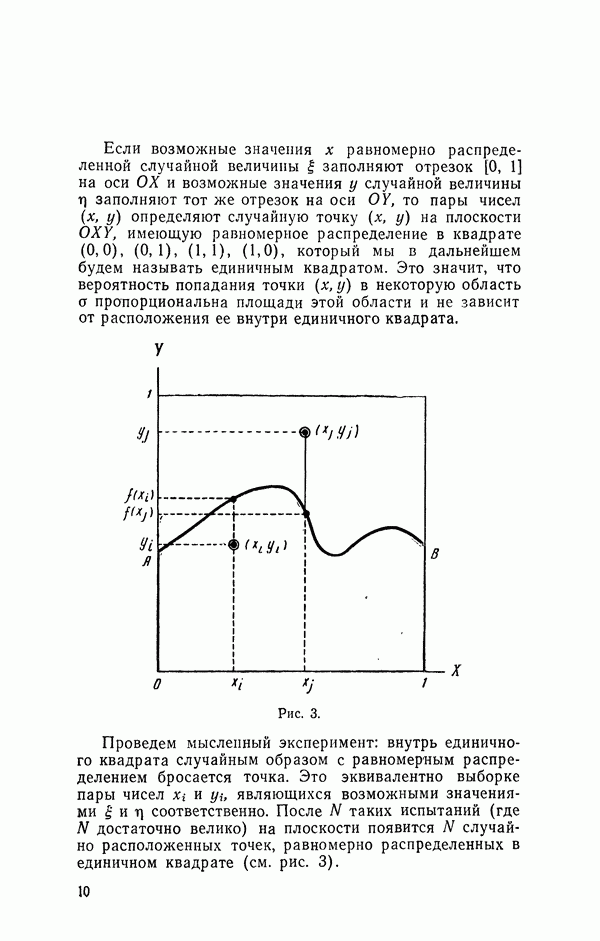
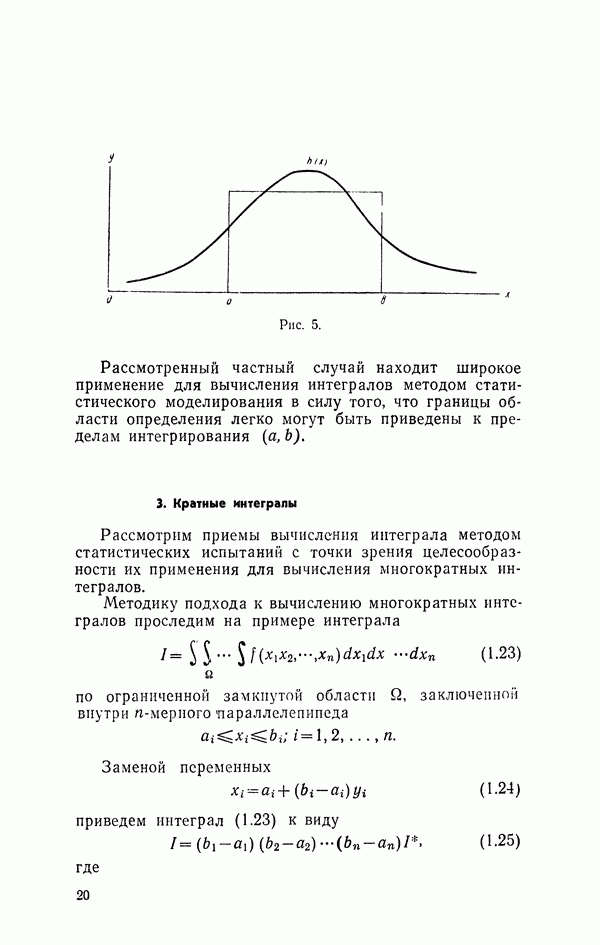
16. Моделирование многоканальной системы

Рассмотрим теперь структуру моделирующего алгоритма для случая многоканальной системы.

Пусть система массового обслуживания имеет каналов, вполне идентичных (с точки зрения длительности обслуживания) и равноправных (в смысле возможности использования для обслуживания данной заявки любого свободного канала).

Будем по-прежнему считать, что в систему поступает ординарный поток заявок с заданным законом распределения. Время возможного ожидания до начала обслуживания — случайная величина с законом распределения ф(т). Длительность обслуживания имеет закон распределения . Процесс функционирования системы рассматривается в интервале времени . Заявки принимаются к обслуживанию в порядке очереди (в порядке поступления в систему). Если для обслуживания данной заявки имеется несколько свободных каналов, то каналы привлекаются к обслуживанию в порядке очереди (в первую очередь привлекается тот канал, который ранее других освободился от обслуживания).

Описанная здесь система близка по характеру к одноканальной системе. Поэтому многие операторы схемы (4. 21) могут быть использованы для построения моделирующего алтритма в нашем случае. Сохраним также

все обозначения, использованные для построения схемы (4.21).

Рассмотрим следующие операторы:

— вычисление момента окончания обслуживания заявки (момента освобождения канала) где — момент начала обслуживания заявки каналом;

— запись полученного в регистр;

— выбор из регистра — наименьшего из каналов, свободных в данный момент времени;

— проверка условия (в момент поступления заявки все каналы заняты);

— проверка условия (заявка покидает систему ранее чем освободится хотя бы один из каналов);

— выбор в качестве момента начала обслуживания величины

— проверка условия (период пребывания заявки в системе целиком принадлежит интервалу моделирования процесса).

Запишем операторную схему моделирующего алгоритма для многоканальной системы, пользуясь также операторами схемы (4.21):

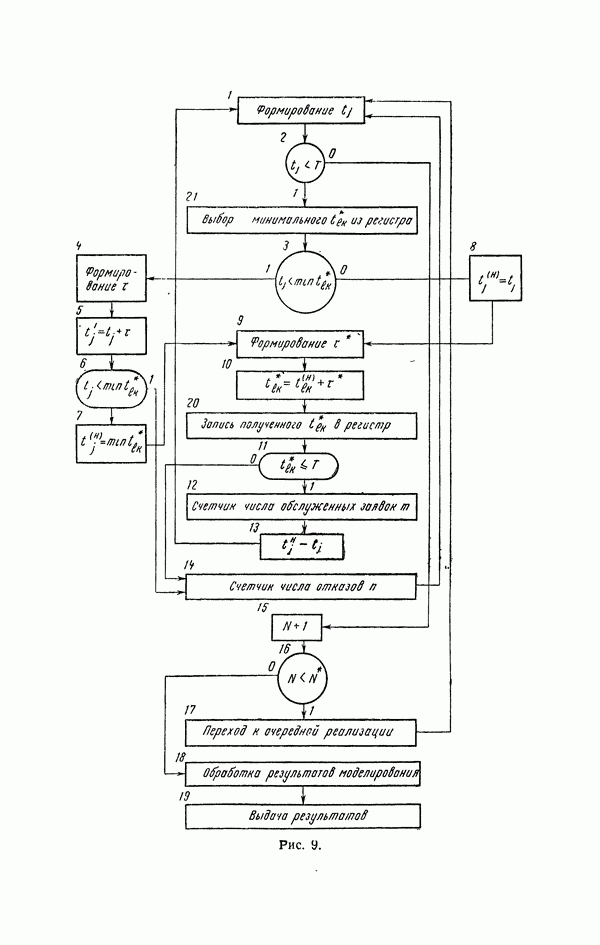
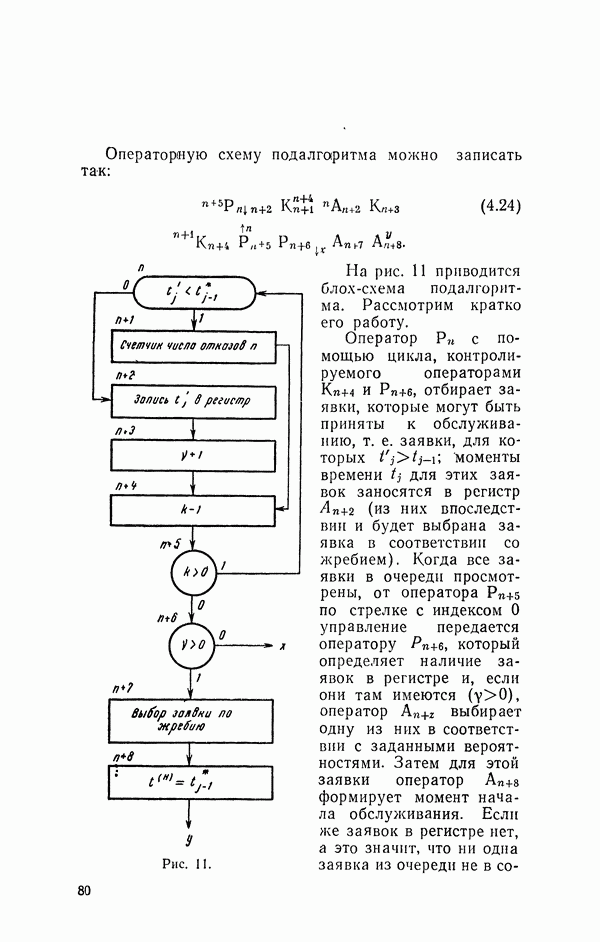
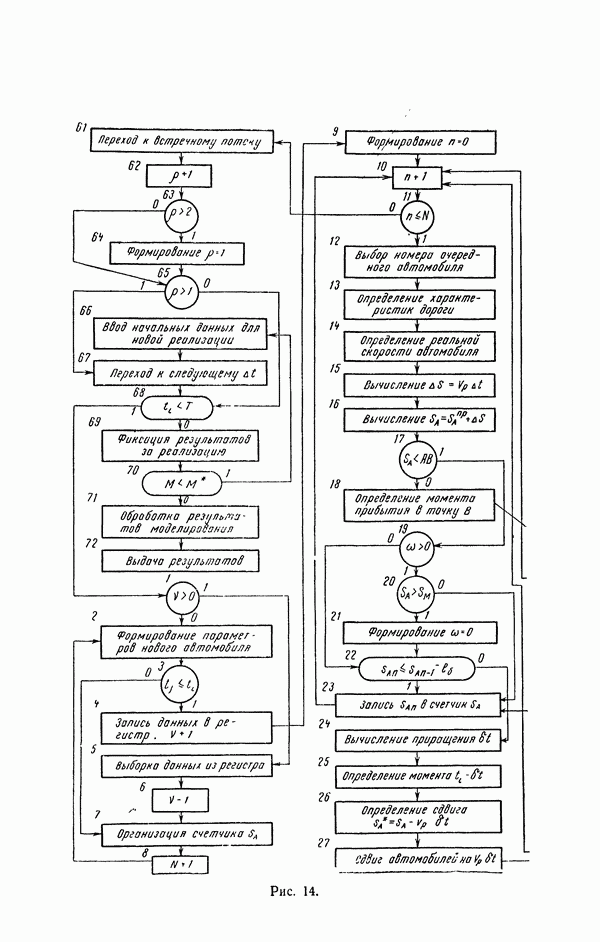
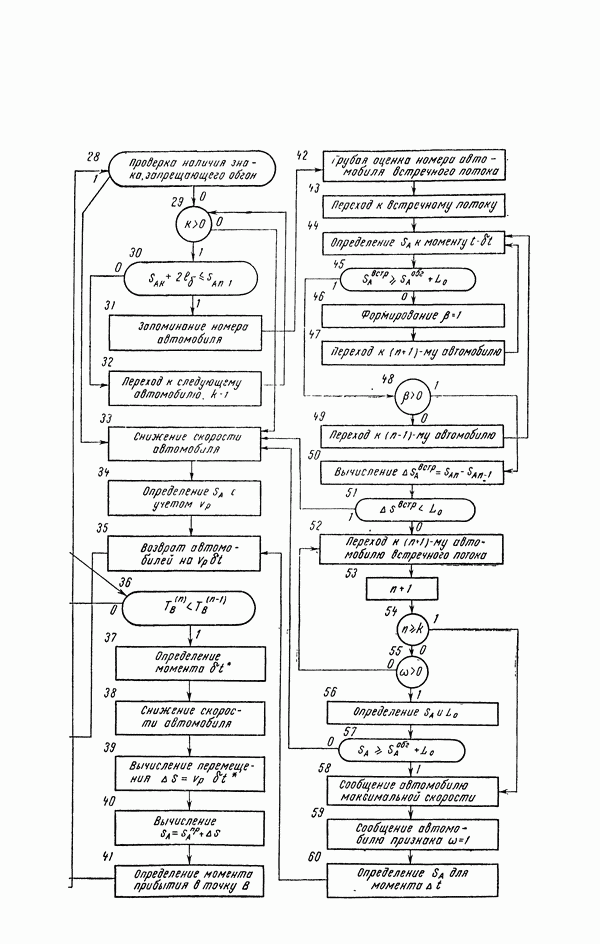
На рис. 9 представлена блок - схема рассматриваемого алгоритма.

Моделирующий алгоритм (4. 22) работает аналогично алгоритму (4.21). Поэтому мы не будет останавливаться подробно на его описании. Отметим только некоторые особенности.

Рис. 9

(см. скан)

Когда оператором определены момент окончания обслуживания заявки каналом, имеется, с сдной стороны, момент окончания обслуживания заявки, а с другой — момент освобождения канала.

Далее как момент окончания обслуживания заявки, сравнивается с Т (оператор Если условие, проверяемое оператором не выполнено — заявка не считается обслуженной и управление передается оператору Для подсчета числа отказов. Когда же условие, проверяемое оператором выполнено, управление передается оператору для подсчета числа обслуженных заявок. Кроме того, рассматривается в этом случае момент освобождения канала. Может случиться, что в данный момент времени имеются и другие свободные каналы. Моменты освобождения их помещены в специальный регистр (ячейку памяти ЭВМ) в порядке возрастания. Оператор записывает в этот регистр очередное значение полученное оператором . В отличие от схемы (4. 21) от оператора по стрелке с индексом 1 управление передается оператору который выбирает из регистра наименьшее и передает управление Таким образом, наличие свободного канала выясняется сравнением - момента поступления очередной заявки — с — минимальным временем освобождения одного из каналов. В случае отрицательного решения вопроса о наличии свободного канала, в момент поступления заявки, величина используется (оператор для определения возможности обслужить заявку. Если данная заявка может быть обслужена, то в качестве момента начала обслуживания опять же выбирается (оператор ). В остальном работа алгоритма (4.22) не отличается от работы алгоритма (4.21).

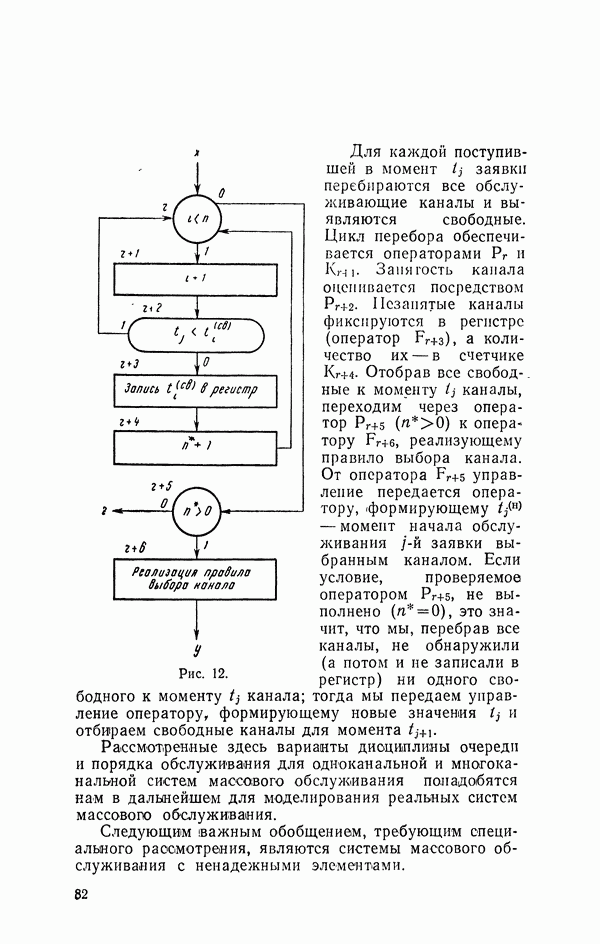
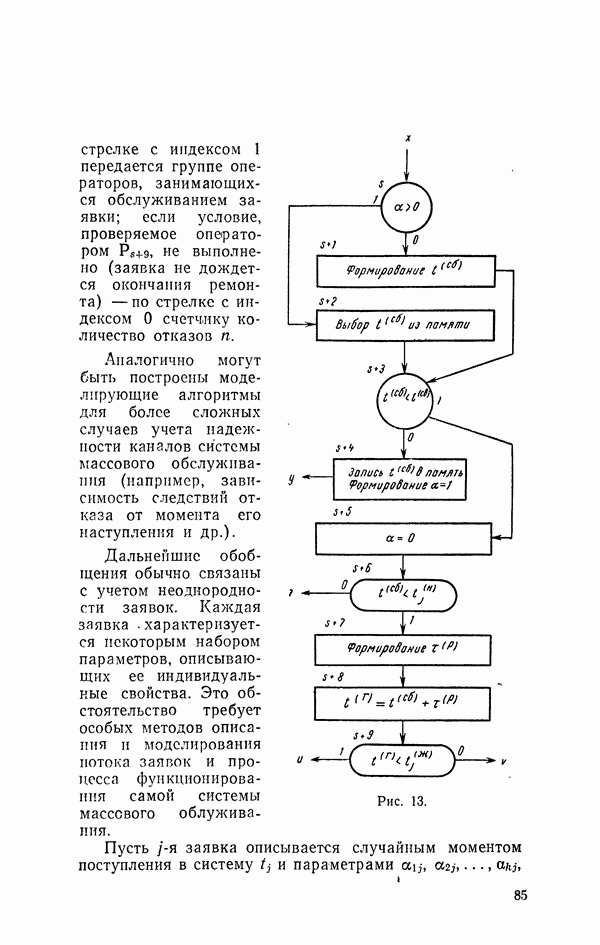
В заключение заметим, что структура моделирующего алгоритма существенно зависит от порядка выбора заявок из очереди для обслуживания (дисциплина очереди заявок) и порядка привлечения к обслуживанию свободных каналов (дисциплина очереди каналов). Некоторые наиболее распространенные варианты дисциплины очереди заявок и каналов мы рассмотрим в следующем параграфе.