| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Требуемое количество операций
Рассматривая различные способы вычисления интеграла методом статистических испытаний, мы ввели N — число испытаний, оговаривая каждый раз, что N достаточно велико. Какую же величину N можно считать достаточной для вычисления интеграла с заданной точностью? Будем говорить, что равенство  имеет точность
имеет точность  с достоверностью а, если вероятность
с достоверностью а, если вероятность

Проследим это на примере второго способа вычисления интеграла на ЭВМ (см. стр. 16). В качестве приближенного значения  интеграла
интеграла  мы брали величину
мы брали величину  Если рассматривать
Если рассматривать  как случайную величину, можно вычислить математическое ожидание I
как случайную величину, можно вычислить математическое ожидание I

и дисперсию

тогда средняя квадратичная ошибка

Свяжем величины а и  с числом испытаний N при помощи неравенства Чебышева (см. [5]):
с числом испытаний N при помощи неравенства Чебышева (см. [5]):

Заменим левую часть неравенства (1.40) выражением из формулы (1.36)

подставляя вместо  его значения, получаем
его значения, получаем

и, решая неравенство относительно N, вычислим

Надо сказать, что формула (1.43), полученная на основании неравенства Чебышева, дает только верхнюю грань величины 
Более точно количество испытаний N можно подсчитать, учитывая, что в рассматриваемом примере (см. стр. 16) величина  симптотически (при
симптотически (при  ) подчиняется нормальному закону распределения. Основываясь на этом факте, перепишем формулу (1.36)
) подчиняется нормальному закону распределения. Основываясь на этом факте, перепишем формулу (1.36)

Величина  выбирается из таблиц нормального распределения для заданного а. Сопоставив равенства (1.40) и (1.44), находим
выбирается из таблиц нормального распределения для заданного а. Сопоставив равенства (1.40) и (1.44), находим

или

отсюда

Этой более точной формулой мы будем пользоваться в дальнейшем для оценки количества испытаний N.
Теперь рассмотрим приемы вычисления многомерных интегралов с точки зрения сравнения этих приемов с обычными кубатурными формулами. Выясним трудоемкость вычисления кратных интегралов методом статистических испытаний. Полное число операций

где  — число операций, затрачиваемое на вычисление одного значения подынтегральной функции
— число операций, затрачиваемое на вычисление одного значения подынтегральной функции

(предположим, что остальные вычисления незначительны).
Число операций также зависит от того, какую точность мы хотим получить, и. следовательно,

Обычно используются кубатурные формулы вида 

где  — точки
— точки  -мерного куба, для вычисления которых требуются
-мерного куба, для вычисления которых требуются  операций, где
операций, где  тоже зависит от заданной точности результата
тоже зависит от заданной точности результата

Очевидно, что сравнивать объемы вычислений методом статистических испытаний и с помощью кубатурных
формул необходимо соблюдая одинаковую точность 
Выясним сначала зависимость  На основании формулы (1.47)
На основании формулы (1.47)

Если говорить о «максимальной» ошибке, то для данного случая можно воспользоваться правилом «трех сигм». Тогда 
Так как максимум значения  достигается при
достигается при  и равен 0,25, можно приблизительно оцепить величину N:
и равен 0,25, можно приблизительно оцепить величину N:

следовательно,  имеет порядок
имеет порядок

для интегралов любой кратности.
Для кубатурных формул

где  зависит от гладкости функции,
зависит от гладкости функции,  число измерений. Таким образом, отношение числа операций
число измерений. Таким образом, отношение числа операций  необходимых при вычислении интеграла методом статистических испытаний, к числу операций
необходимых при вычислении интеграла методом статистических испытаний, к числу операций  при счете по кубатурным формулам составляет
при счете по кубатурным формулам составляет

Из формулы (1.57) следует, что метод статистических испытаний имеет преимущества уже при

для малых  .
.
Для наглядности приведем числовые данные о требуемом количестве испытаний.
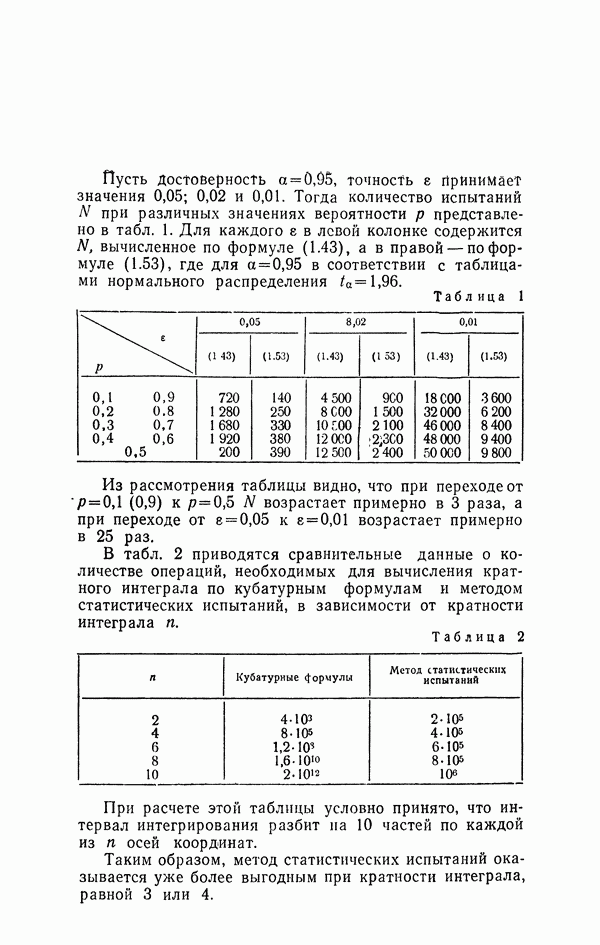
Пусть достоверность  точность
точность  принимает значения 0,05; 0,02 и 0,01. Тогда количество испытаний N при различных значениях вероятности
принимает значения 0,05; 0,02 и 0,01. Тогда количество испытаний N при различных значениях вероятности  представлено в табл. 1. Для каждого
представлено в табл. 1. Для каждого  в левой колонке содержится N, вычисленное по формуле (1.43), а в правой — по формуле (1.53), где для
в левой колонке содержится N, вычисленное по формуле (1.43), а в правой — по формуле (1.53), где для  в соответствии с таблицами нормального распределения
в соответствии с таблицами нормального распределения 
Таблица 1

Из рассмотрения таблицы видно, что при переходе от р = 0,1 (0,9) к р = 0,5 N возрастает примерно в 3 раза, а при переходе от  возрастает примерно в 25 раз.
возрастает примерно в 25 раз.
В табл. 2 приводятся сравнительные данные о количестве операций, необходимых для вычисления кратного интеграла по кубатурным формулам и методом статистических испытаний, в зависимости от кратности интеграла 
Таблица 2

При расчете этой таблицы условно принято, что интервал интегрирования разбит на 10 частей по каждой из  осей координат.
осей координат.
Таким образом, метод статистических испытаний оказывается уже более выгодным при кратности интеграла, равной 3 или 4.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ (МОНТЕ КАРЛО)
- 2. Попадание случайной величины в заданный интервал. Среднее значение функции до случайной величины
- 3. Кратные интегралы
- 4. Требуемое количество операций
- Глава II. ПОЛУЧЕНИЕ И ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ
- 6. Получение случайных чисел с заданным законом распределения
- 7. Приближенные способы преобразования случайных чисел
- 8. Моделирование случайных векторов
- Глава III. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
- 10. Этапы формализации реальных сложных систем
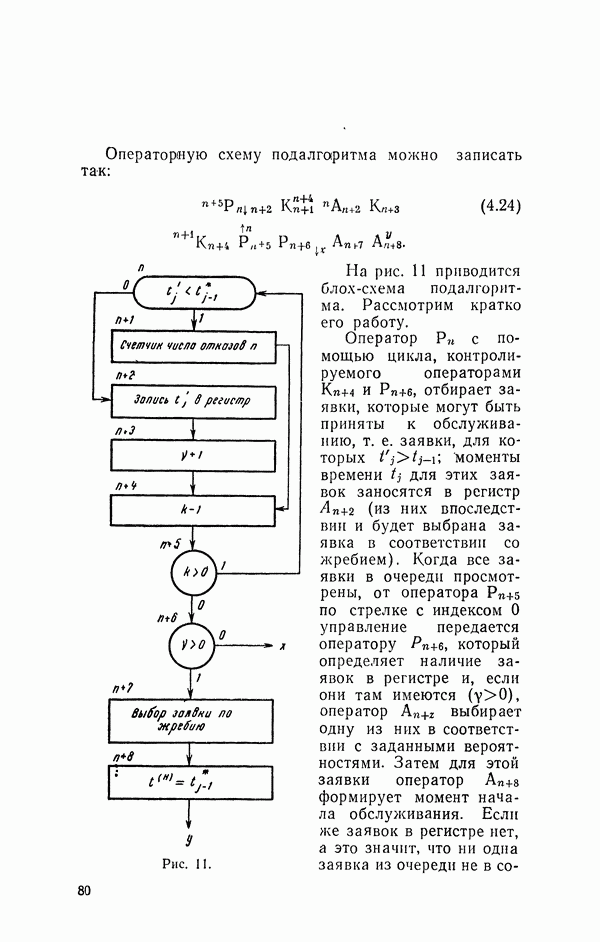
- 11. Операторная схема моделирующего алгоритма
- 12. Метод статистического моделирования как аппарат анализа сложных систем
- Глава IV. СТАТИСТИЧЕСКИЕ МОДЕЛИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
- 13. Понятие системы массового обслуживания
- 14. Моделирование потоков заявок
- 15. Моделирование одноканальной системы массового обслуживания
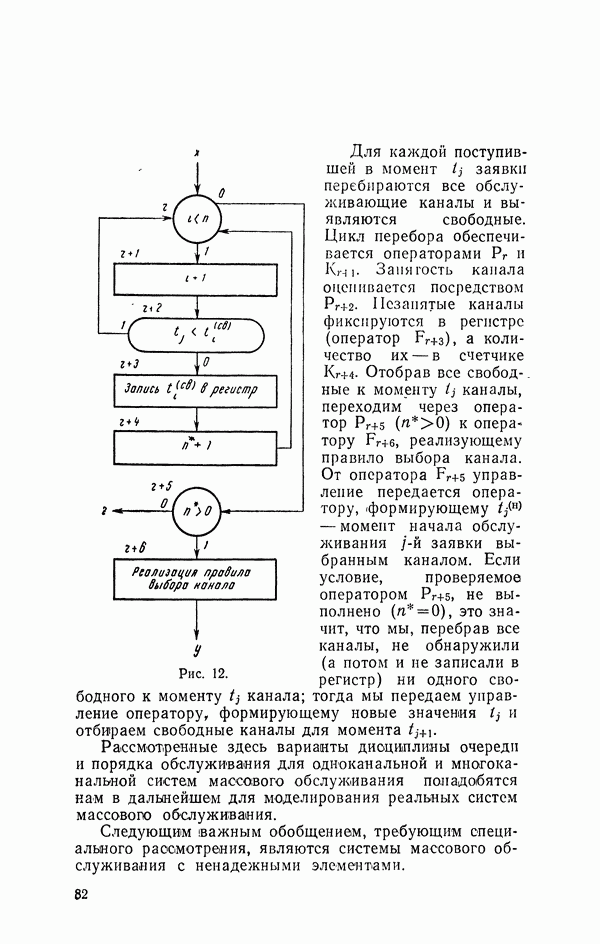
- 16. Моделирование многоканальной системы
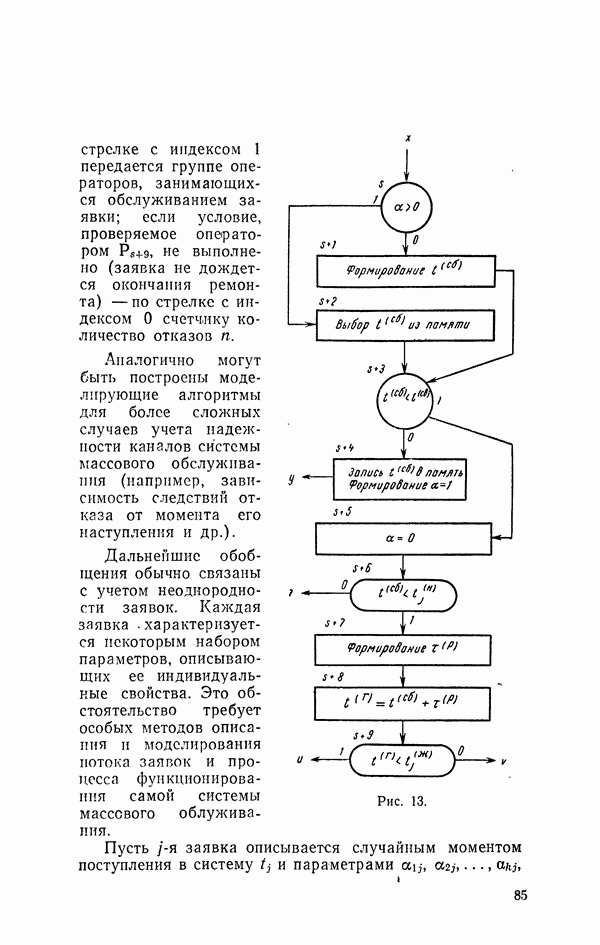
- 17. Модификаций систем массового обслуживания
- Глава V. МОДЕЛИРОВАНИЕ АВТОМОБИЛЬНОГО ДВИЖЕНИЯ
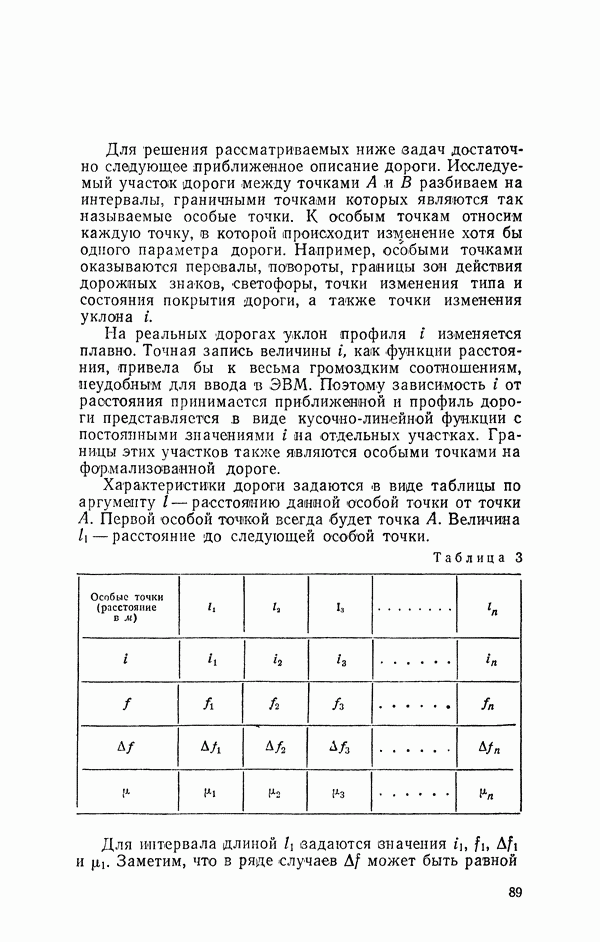
- 19. Описание потока автомобилей
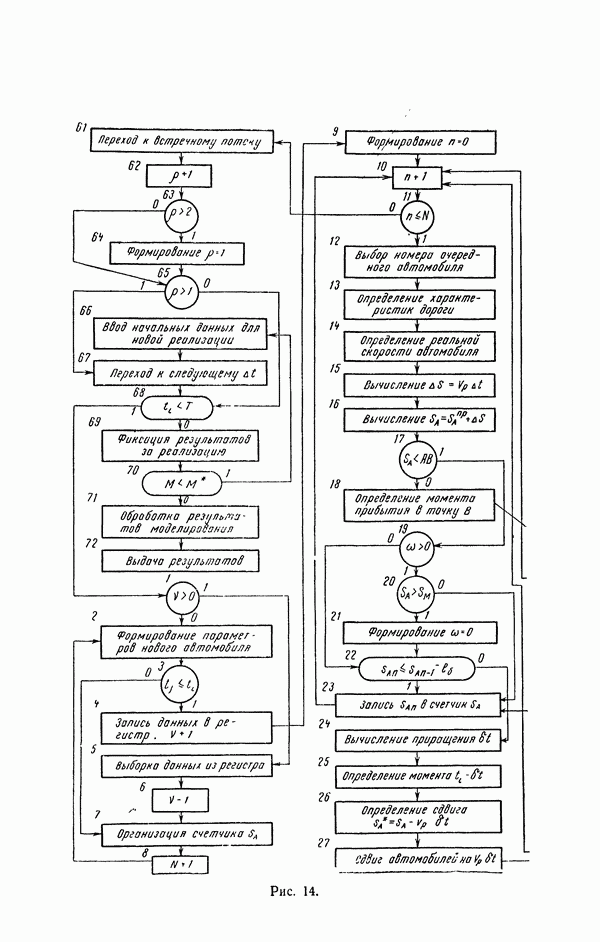
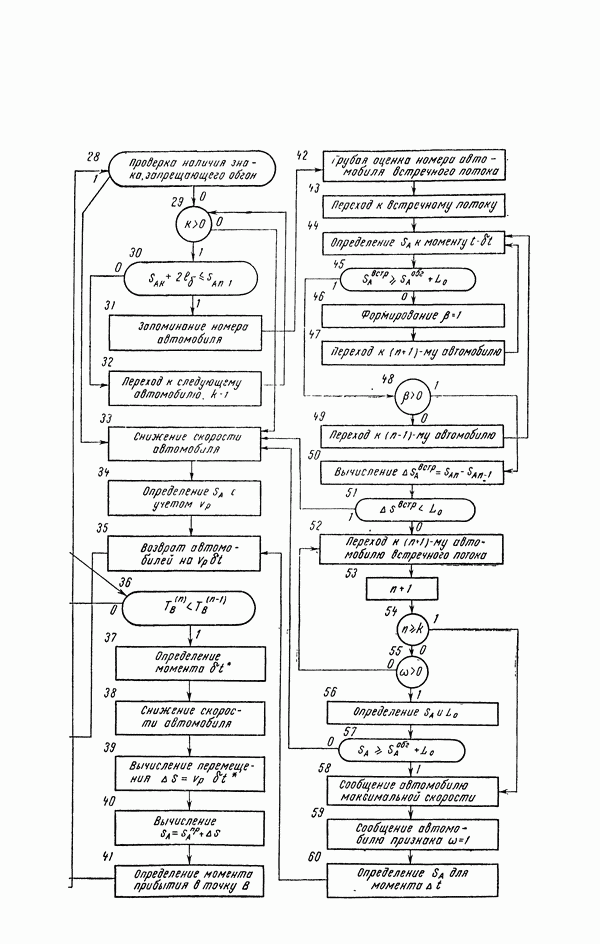
- 20. Структура моделирующего алгоритма
- 21. Исходные данные и результаты моделирования