| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Определенный интеграл
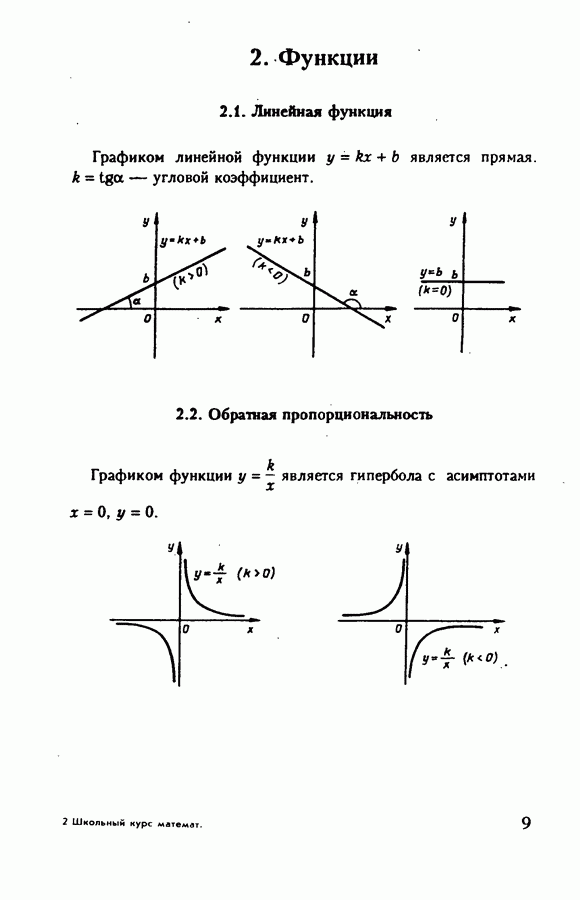
3.1. Формула Ньютона-Лейбница
Если  — первообразная для
— первообразная для  на промежутке X и если
на промежутке X и если  — точки из этого промежутка X, то
— точки из этого промежутка X, то
 (формула Ньютона-Лейбница),
(формула Ньютона-Лейбница),
где  — определенный интеграл;
— определенный интеграл;  — пределы интегрирования;
— пределы интегрирования;  — подынтегральная функция.
— подынтегральная функция.
3.2. Свойства определенного интеграла

Если  то
то  (аддитивное свойство интеграла).
(аддитивное свойство интеграла).

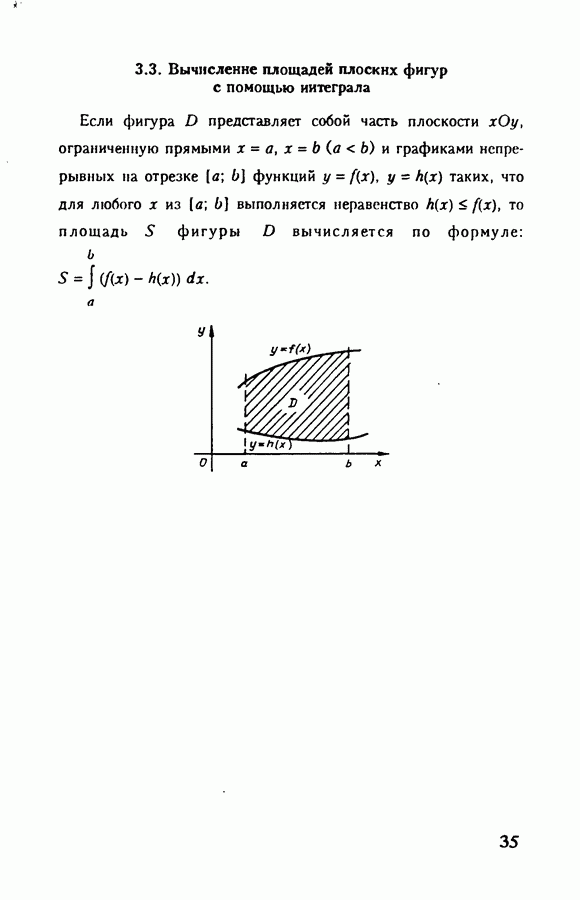
3.3. Вычисление площадей плоских фигур с помощью интеграла
Если фигура  представляет собой часть плоскости
представляет собой часть плоскости  ограниченную прямыми
ограниченную прямыми  и графиками непрерывных на отрезке
и графиками непрерывных на отрезке  функций
функций  таких, что для любого х из
таких, что для любого х из  выполняется неравенство
выполняется неравенство  то площадь
то площадь  фигуры
фигуры  вычисляется по формуле:
вычисляется по формуле: 

| << Предыдущий параграф | Следующий параграф >> |
- АЛГЕБРА
- 2. Функции
- 2.7. Свойства функций
- 2.8. Построение графиков функций с помощью преобразований известных графиков
- 3. Уравнения
- 4. Неравенства
- 5. Прогрессии
- 5.1. Арифметическая прогрессия
- 5.2. Геометрическая прогрессия
- ТРИГОНОМЕТРИЯ
- 1. Тригонометрические функции
- 2. Формулы тригонометрии
- ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- 1. Производная
- 2. Исследование функций с помощью производной
- 2.2. Исследование на экстремум
- 2.3. Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке
- ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
- 1. Первообразная
- 2. Неопределенный интеграл
- 3. Определенный интеграл
- ПЛАНИМЕТРИЯ
- 1. Треугольники
- 1.4. Произвольный треугольник
- 2. Четырехугольники
- 2.1. Выпуклый четырехугольник
- 2.2. Параллелограмм
- 2.3. Трапеция
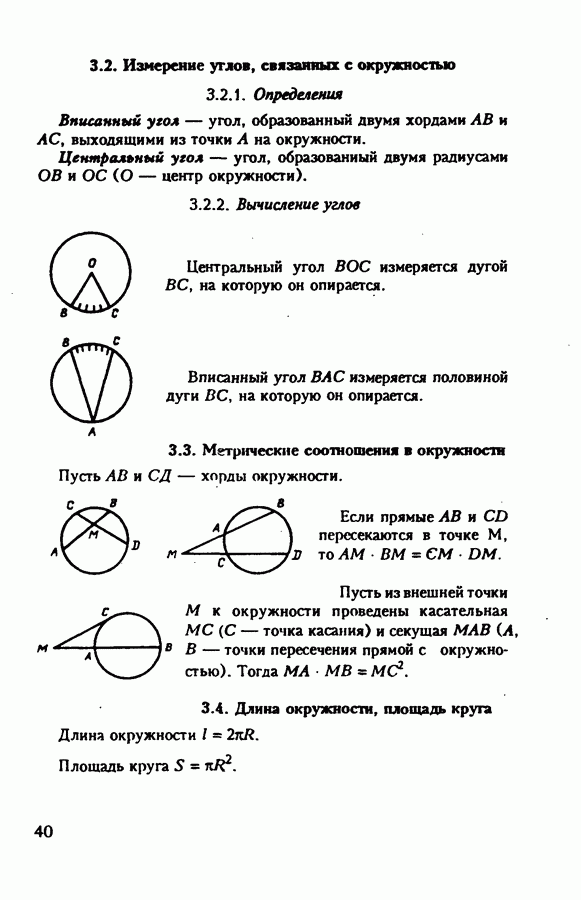
- 3. Окружность и круг
- 3.2. Измерение углов, связанных с окружностью
- 3.3. Метрические соотношения в окружности
- 3.4. Длина окружности, площадь круга
- 3.5. Длина дуги, площадь сектора
- СТЕРЕОМЕТРИЯ
- 1. Основные теоремы, используемые для обоснования чертежа
- 2. Пирамида
- 3. Призма
- 4. Круглые тела
- 5. Описанные шары
- 6. Вписанные шары