| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
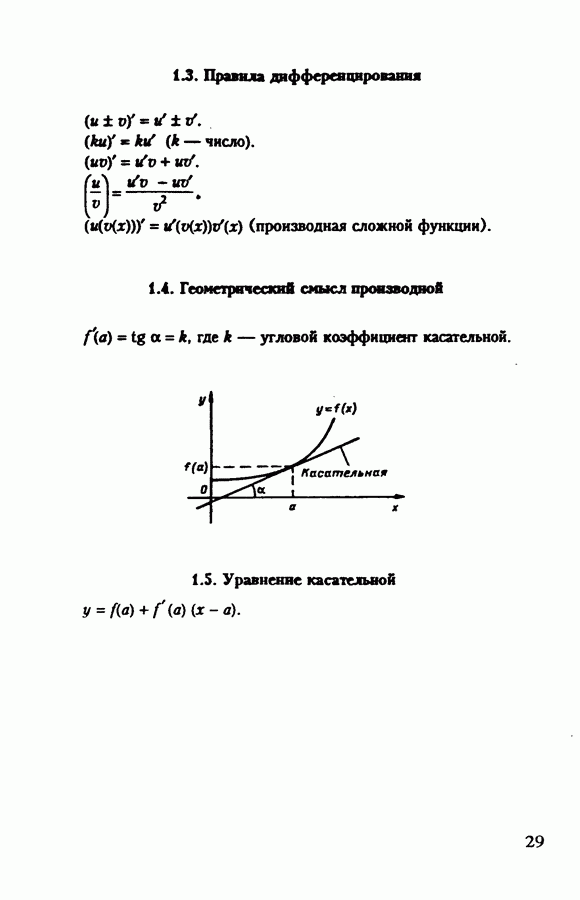
1.4. Произвольный треугольник
1.4.1. Четыре замечательные точки в треугольнике
Медианы треугольника пересекаются в одной точке и делятся в ней в отношении  считая от вершины. Эта точка называется центром тяжести.
считая от вершины. Эта точка называется центром тяжести.
Высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром.
Биссектрисы треугольника пересекаются в одной точке. Эта точка является центром вписанной окружности.
Перпендикуляры, проведенные к сторонам треугольника через их середины, пересекаются в одной точке. Эта точка является центром описанной окружности.
1.4.2. Средняя линия треугольника
Параллельна основанию.
Равна половине основания.
Делит пополам любой отрезок, соединяющий вершину треугольника с какой-либо точкой основания.
1.4.3. Свойство биссектрисы треугольника
Пусть в треугольнике  проведена биссектриса
проведена биссектриса  Тогда
Тогда  (биссектриса делит основание на части, пропорциональные боковым сторонам).
(биссектриса делит основание на части, пропорциональные боковым сторонам).

1.4.4. Определение вида треугольника по его сторонам
Пусть с — наибольшая из трех сторон треугольника.
Если  то треугольник остроугольный.
то треугольник остроугольный.
Если  то треугольник прямоугольный.
то треугольник прямоугольный.
Если  то треугольник тупоугольный.
то треугольник тупоугольный.
1.4.5. Площадь

1.4.6. Формулы для вычисления радиусов R и r

1.4.7. Соотношения между сторонами и углами
 (теорема косинусов).
(теорема косинусов).
 (теорема синусов).
(теорема синусов).
1.4.8. Три важные теоремы о площадях
Если два треугольника подобны, то их площади относятся как квадраты соответствующих сторон.
Если у двух треугольников равны основания, то площади относятся как соответствующие высоты.
Если одна высота одного треугольника равна одной высоте другого треугольника, то площади относятся как стороны, к которым проведены эти высоты.
| << Предыдущий параграф | Следующий параграф >> |
- АЛГЕБРА
- 2. Функции
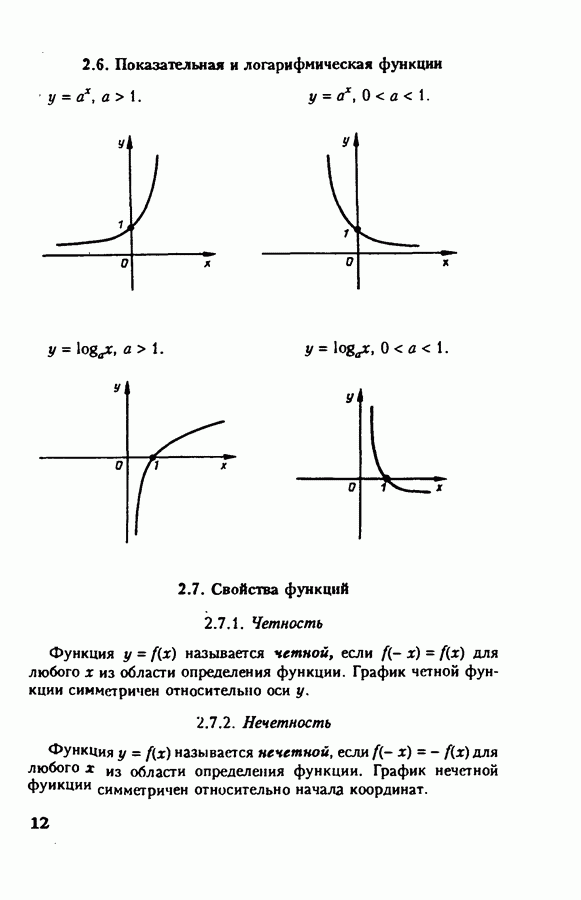
- 2.7. Свойства функций
- 2.8. Построение графиков функций с помощью преобразований известных графиков
- 3. Уравнения
- 4. Неравенства
- 5. Прогрессии
- 5.1. Арифметическая прогрессия
- 5.2. Геометрическая прогрессия
- ТРИГОНОМЕТРИЯ
- 1. Тригонометрические функции
- 2. Формулы тригонометрии
- ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- 1. Производная
- 2. Исследование функций с помощью производной
- 2.2. Исследование на экстремум
- 2.3. Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке
- ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
- 1. Первообразная
- 2. Неопределенный интеграл
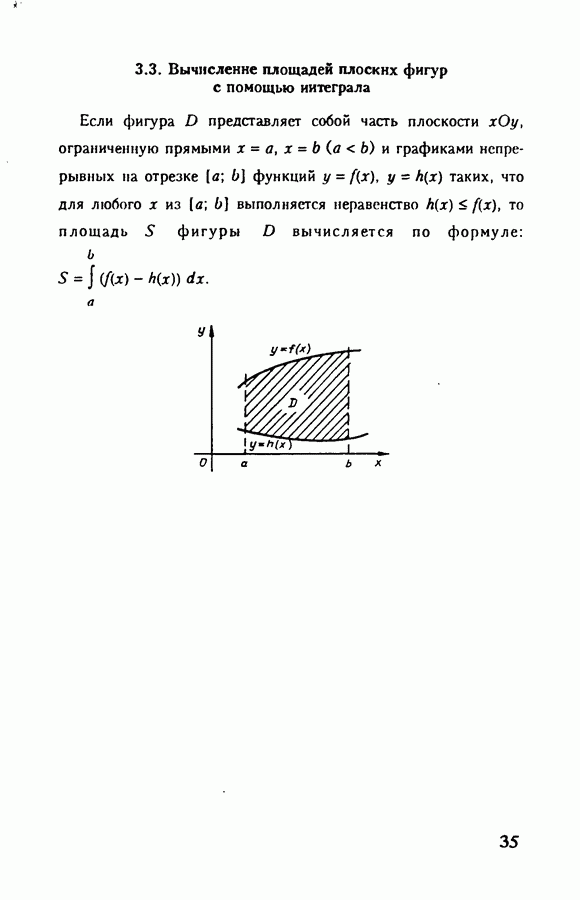
- 3. Определенный интеграл
- ПЛАНИМЕТРИЯ
- 1. Треугольники
- 1.4. Произвольный треугольник
- 2. Четырехугольники
- 2.1. Выпуклый четырехугольник
- 2.2. Параллелограмм
- 2.3. Трапеция
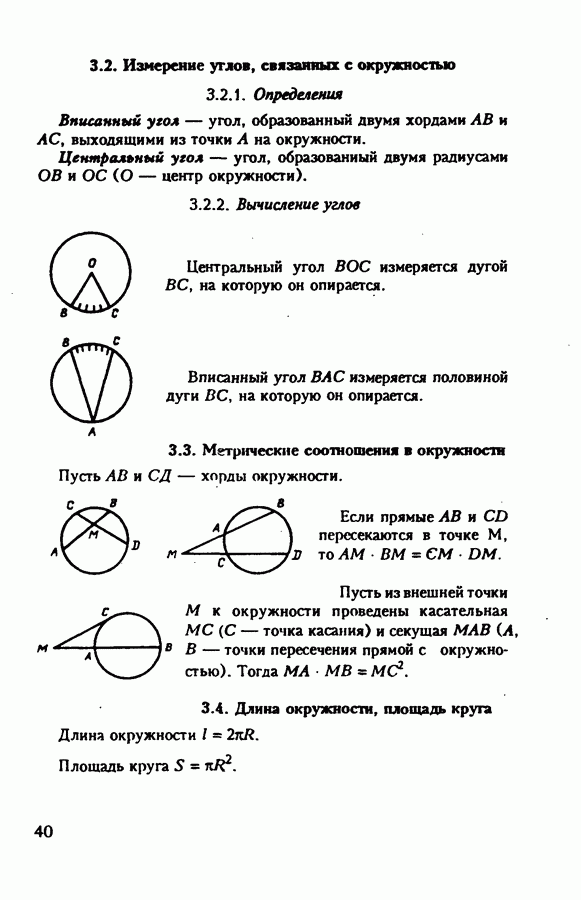
- 3. Окружность и круг
- 3.2. Измерение углов, связанных с окружностью
- 3.3. Метрические соотношения в окружности
- 3.4. Длина окружности, площадь круга
- 3.5. Длина дуги, площадь сектора
- СТЕРЕОМЕТРИЯ
- 1. Основные теоремы, используемые для обоснования чертежа
- 2. Пирамида
- 3. Призма
- 4. Круглые тела
- 5. Описанные шары
- 6. Вписанные шары