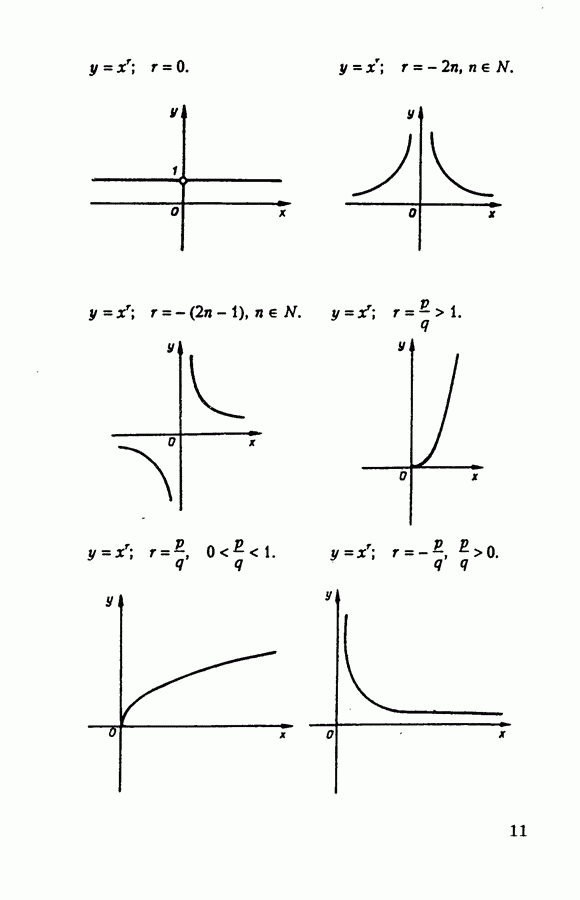| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Вписанные шары
6.1. Шар и пирамида
Центр вписанного шара — точка пересечения биссекторных плоскостей, построенных для всех имеющихся в пирамиде двугранных углов; если эти биссекторные плоскости не имеют общей точки, то шар вписать нельзя.
Частный случай: боковые грани пирамиды равнонаклонены к плоскости основания. Тогда:
шар вписать можно;
центр О шара лежит на высоте пирамиды, конкретнее — это точка пересечения высоты с биссектрисой угла между апофемой и проекцией этой апофемы на плоскость основания.
6.2. Шар и прямая призма
В прямую призму можно вписать шар тогда и только тогда, когда:
в основание призмы можно вписать окружность,
диаметр этой окружности равен высоте призмы.
Центром шара служит середина отрезка, соединяющего центры вписанных в основания окружностей.

где  — радиус вписанного шара;
— радиус вписанного шара;  — радиус вписанной в основание окружности; Н — высота призмы.
— радиус вписанной в основание окружности; Н — высота призмы.
6.3. Шар и цилиндр
В цилиндр можно вписать шар тогда и только тогда, когда осевое сечение цилиндра — квадрат (такой цилиндр иногда называют равносторонним). Центром шара служит центр симметрии осевого сечения цилиндра.
6.4. Шар и конус
В конус можно вписать шар всегда. Центром шара служит центр окружности, вписанной в осевое сечение конуса.
6.5. Шар и усеченный конус
В усеченный конус можно вписать шар тогда и только тогда, когда 
где  — радиусы оснований;
— радиусы оснований;  — образующая.
— образующая.
Центром шара служит середина отрезка, соединяющего центры оснований.

где  — радиус вписанного шара;
— радиус вписанного шара;  — высота усеченного конуса.
— высота усеченного конуса.
| << Предыдущий параграф |
- АЛГЕБРА
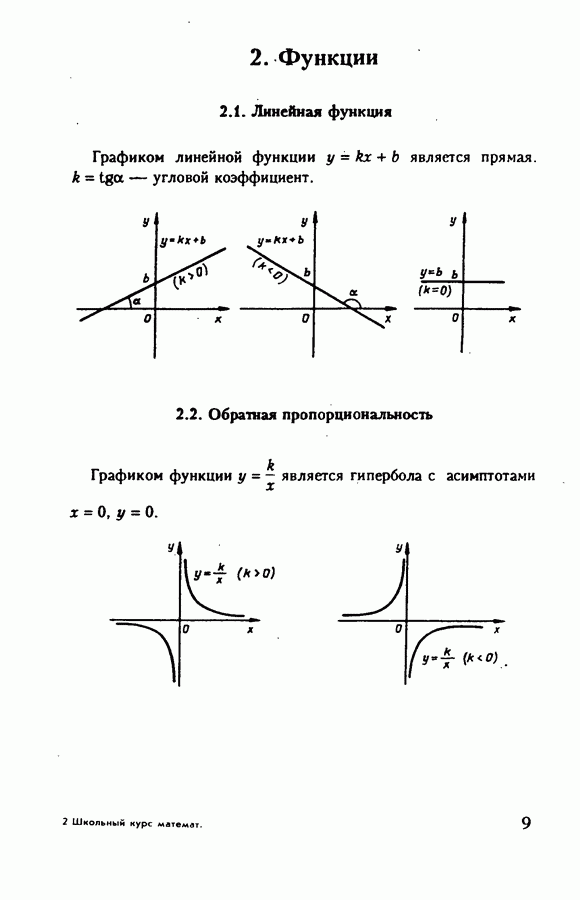
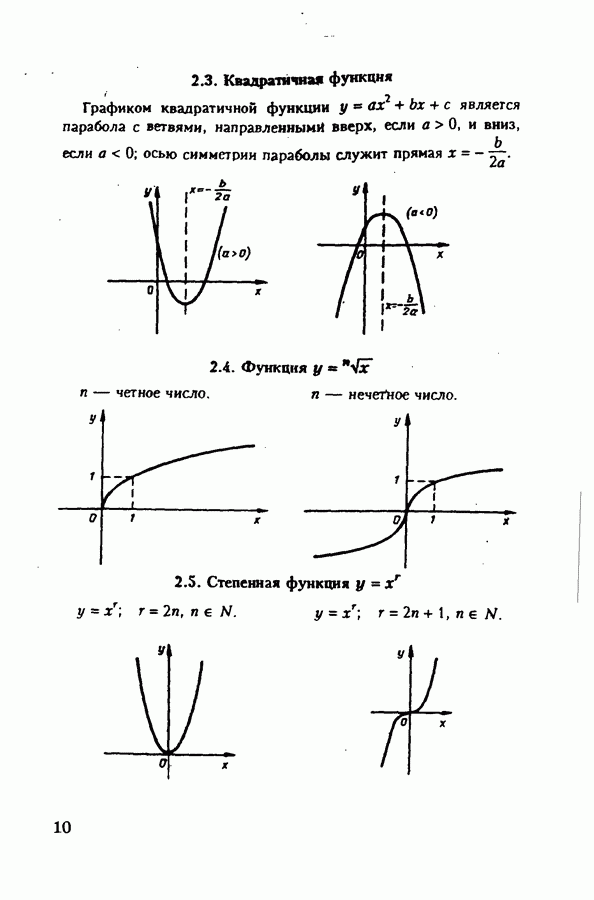
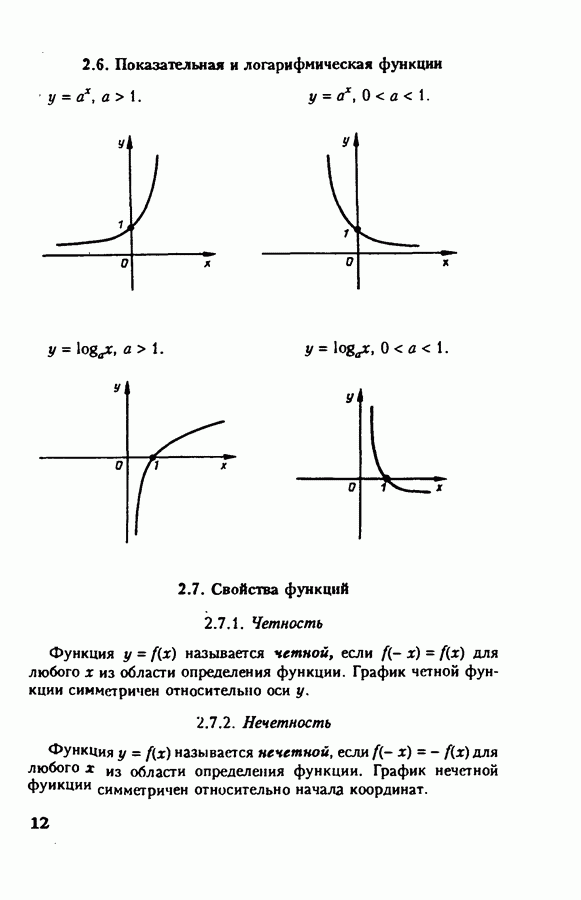
- 2. Функции
- 2.7. Свойства функций
- 2.8. Построение графиков функций с помощью преобразований известных графиков
- 3. Уравнения
- 4. Неравенства
- 5. Прогрессии
- 5.1. Арифметическая прогрессия
- 5.2. Геометрическая прогрессия
- ТРИГОНОМЕТРИЯ
- 1. Тригонометрические функции
- 2. Формулы тригонометрии
- ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- 1. Производная
- 2. Исследование функций с помощью производной
- 2.2. Исследование на экстремум
- 2.3. Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке
- ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
- 1. Первообразная
- 2. Неопределенный интеграл
- 3. Определенный интеграл
- ПЛАНИМЕТРИЯ
- 1. Треугольники
- 1.4. Произвольный треугольник
- 2. Четырехугольники
- 2.1. Выпуклый четырехугольник
- 2.2. Параллелограмм
- 2.3. Трапеция
- 3. Окружность и круг
- 3.2. Измерение углов, связанных с окружностью
- 3.3. Метрические соотношения в окружности
- 3.4. Длина окружности, площадь круга
- 3.5. Длина дуги, площадь сектора
- СТЕРЕОМЕТРИЯ
- 1. Основные теоремы, используемые для обоснования чертежа
- 2. Пирамида
- 3. Призма
- 4. Круглые тела
- 5. Описанные шары
- 6. Вписанные шары