| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Сверточные коды.
Рассмотренный цепной код является простейшим случаем сверточных кодов. В основу сверточного кодирования положен принцип формирования последовательности - проверочных элементов линейной комбинацией элементов информационной последовательности, поступающей непрерывно на вход кодирующего устройства. Сверточные коды могут иметь произвольную скорость  Кодер сверточного кода имеет k входов и
Кодер сверточного кода имеет k входов и  выходов. Эти коды могут быть разделимыми и неразделимыми. В последнем случае в каждый дискретный момент времени на входы кодирующего устройства поступают k информационных символов, а с выходов считываются
выходов. Эти коды могут быть разделимыми и неразделимыми. В последнем случае в каждый дискретный момент времени на входы кодирующего устройства поступают k информационных символов, а с выходов считываются  символов, из которых k символов являются информационными, а остальные
символов, из которых k символов являются информационными, а остальные  линейными комбинациями информационных последовательностей и образуют последовательность проверочных элементов. Если передача информации происходит по одному каналу, то к выходу кодирующего устройства подключается специальная коммутирующая схема.
линейными комбинациями информационных последовательностей и образуют последовательность проверочных элементов. Если передача информации происходит по одному каналу, то к выходу кодирующего устройства подключается специальная коммутирующая схема.
Представим входные информационные последовательности в виде k полиномов:

Выходные проверочные последовательности можно представить в виде  полиномов:
полиномов:

Поскольку в сверточном коде проверочные последовательности являются линейными комбинациями информационных последовательностей, то согласно алгебре многочленов проверочная последовательность может быть записана в виде

где  . Полиномы
. Полиномы  называются образующими (по терминологии циклических кодов). Если
называются образующими (по терминологии циклических кодов). Если  — наибольшая степень образующих полиномов, то любой информационный элемент будет оказывать влияние на проверочную последовательность
— наибольшая степень образующих полиномов, то любой информационный элемент будет оказывать влияние на проверочную последовательность  на протяжение не более
на протяжение не более  тактов. В течение этого времени с выхода кодирующего устройства будет считано
тактов. В течение этого времени с выхода кодирующего устройства будет считано  символов. Величину
символов. Величину  называют кодовым ограничением сверточного кода. Для сверточных кодов со скоростью передачи
называют кодовым ограничением сверточного кода. Для сверточных кодов со скоростью передачи  число образующих полиномов равно
число образующих полиномов равно  Начальным кодовым словом сверточного кода называют первую совокупность символов на выходах кодирующего устройства.
Начальным кодовым словом сверточного кода называют первую совокупность символов на выходах кодирующего устройства.
Для пояснения принципа кодирования рассмотрим случай, когда скорость кода равна  . Тогда число образующих полиномов равно
. Тогда число образующих полиномов равно  Возьмем образующий полином степени
Возьмем образующий полином степени  :
:

При поступлении на вход кодера информационной последовательности  на выходе получаем информационную последовательность
на выходе получаем информационную последовательность  совпадающую с исходной, и проверочную последовательность
совпадающую с исходной, и проверочную последовательность  Представляя эти последовательности в виде полиномов и используя (7.19), имеем
Представляя эти последовательности в виде полиномов и используя (7.19), имеем

Таким образом, кодирование заключается в вычислении произведения  . С учетом того, что операция умножения происходит в поле
. С учетом того, что операция умножения происходит в поле  вычисление
вычисление  осуществляется линейным многотактным фильтром, содержащим регистры и сумматор по модулю 2 (но без обратных связей). Значения проверочных элементов определяются выражением
осуществляется линейным многотактным фильтром, содержащим регистры и сумматор по модулю 2 (но без обратных связей). Значения проверочных элементов определяются выражением

Если на вход кодирующего устройства информационные символы поступают поочередно, то проверочные разряды b, в соответствии с (7.20) будут формироваться следующим образом:


Из (7.22) видно, что формирование проверочных разрядов происходит суммированием по модулю 2 каждого информационного разряда с некоторым набором предыдущих разрядов. Подобная рекуррентная процедура и объясняет название этих кодов как непрерывных (рекуррентных). Рассмотренный выше цепной код является простейшим частным случаем такого кода. Очевидно, что структура сверточного кода полностью определяется образующим полиномом.
При декодировании принятые последовательности информационных и проверочных символов могут вследствие ошибок отличаться от переданных. Декодирование сверточного кода осуществляется следующим образом. Принятая информационная последовательность кодируется так же, как это делается на передаче, далее выполняется сложение по модулю 2 с принятой проверочной последовательностью. В результате получается корректирующая последовательность, по которой можно исправить ошибки.
Существуют различные процедуры декодирования, среди которых наиболее эффективен алгоритм Возенкрафта — Фано [7.1, 7.2]. Подробнее со свойствами сверточных кодов можно ознакомиться в [7.1].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
- Модулированные сигналы.
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
- Основы микропроцессорной реализации модуляторов УПС.
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
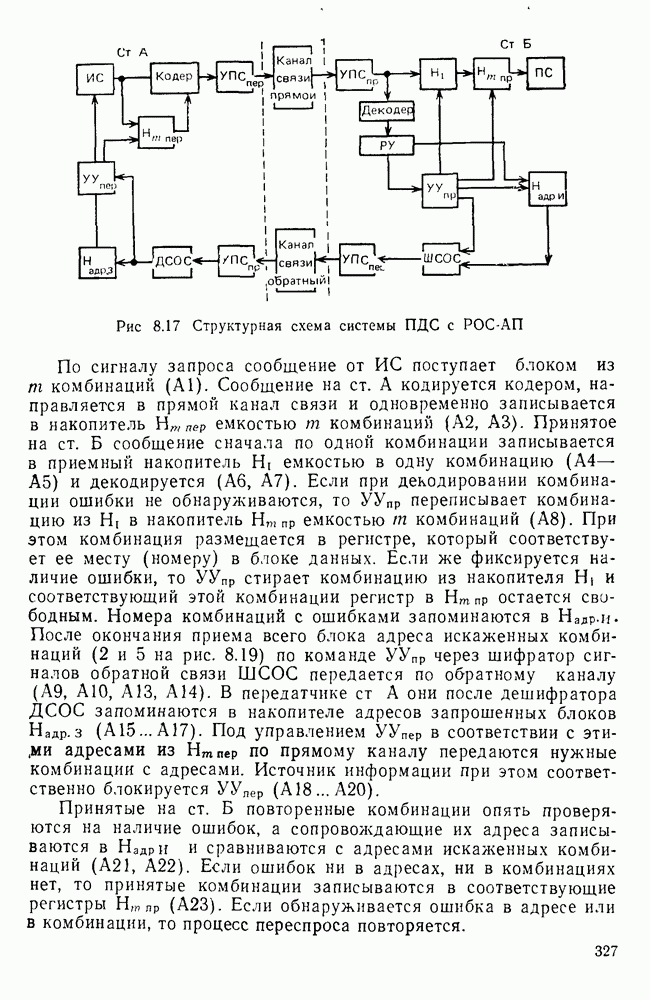
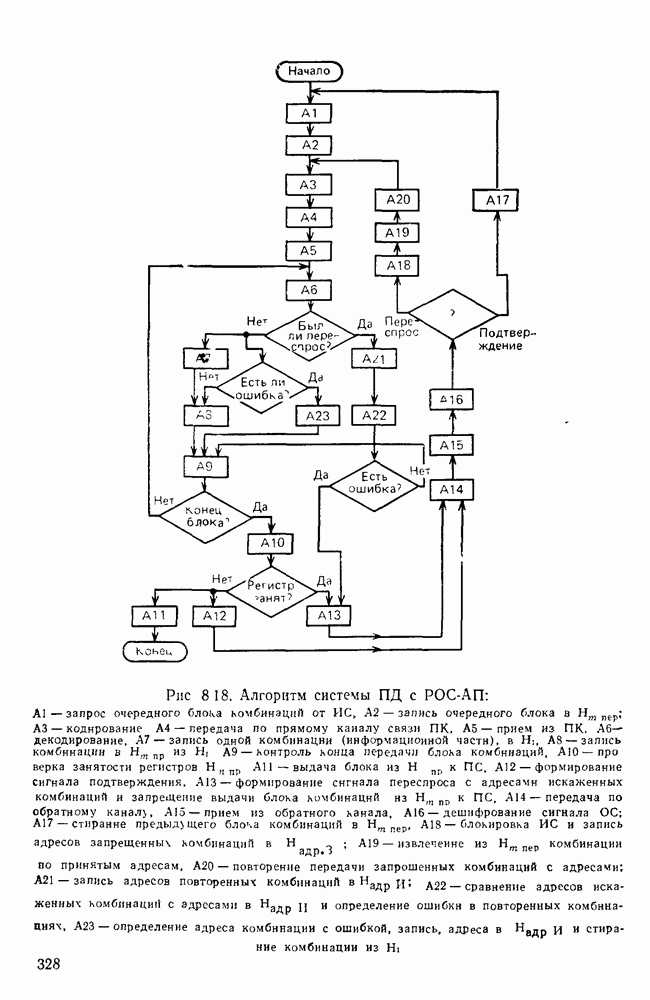
- Система с РОС и адресным переспросом РОС-АП.
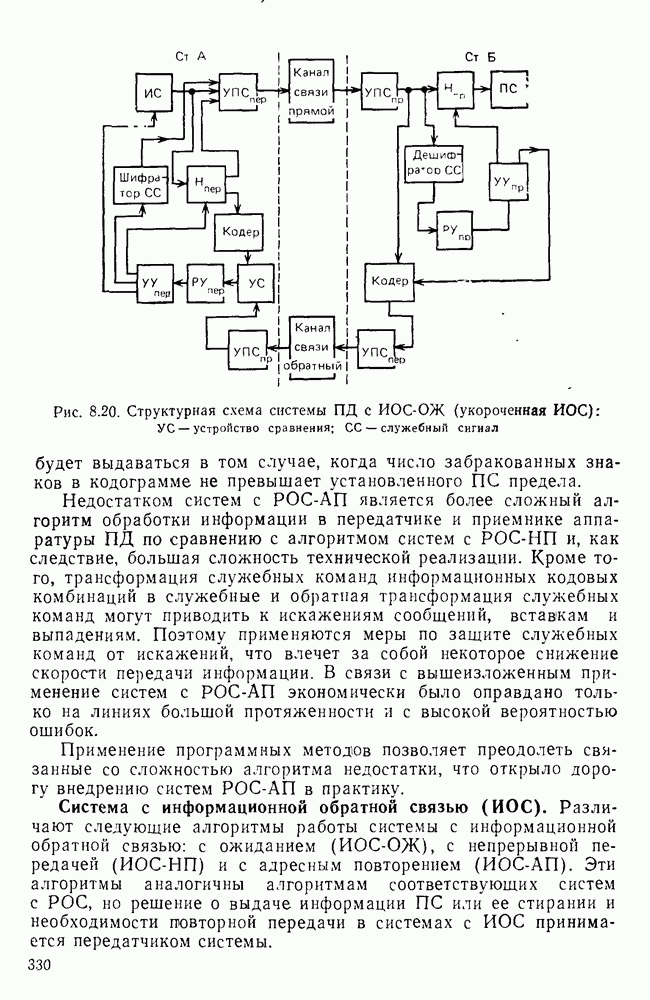
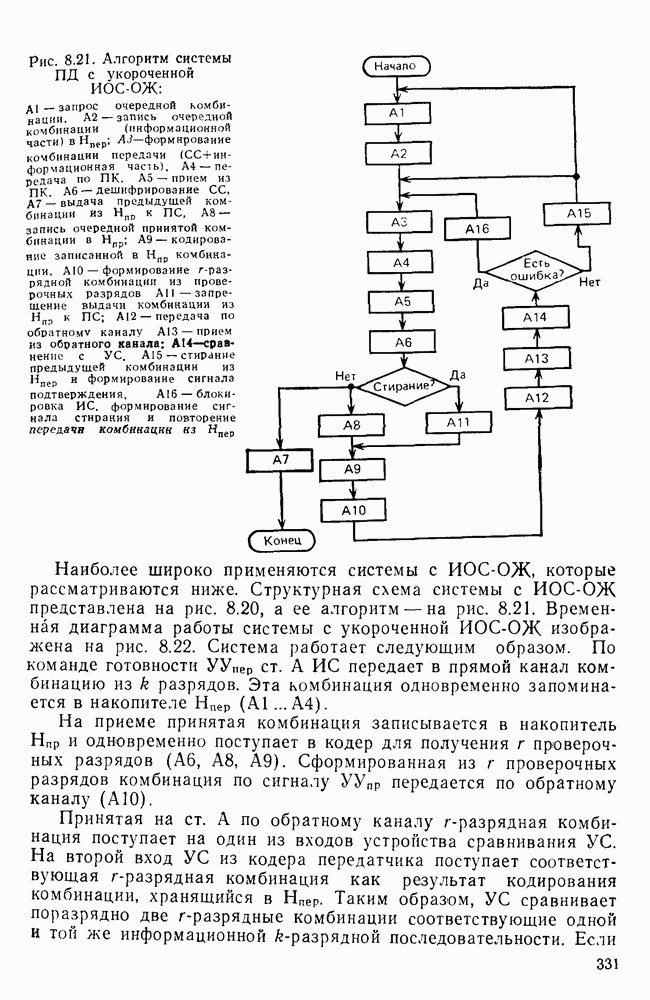
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ