| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
Общие положения.
Как было показано в разд. 6.2, сигналы, в том числе модулированные по амплитуде, частоте и фазе, в пределах единичного интервала то можно представить в виде суммы некоторых ортонормированных функций времени  взятых с соответствующими весовыми коэффициентами
взятых с соответствующими весовыми коэффициентами 
Связь между сигналом  представляемым рядом Фурье, базисными функциями
представляемым рядом Фурье, базисными функциями  и спектральными коэффициентами
и спектральными коэффициентами  выражается известной формулой
выражается известной формулой


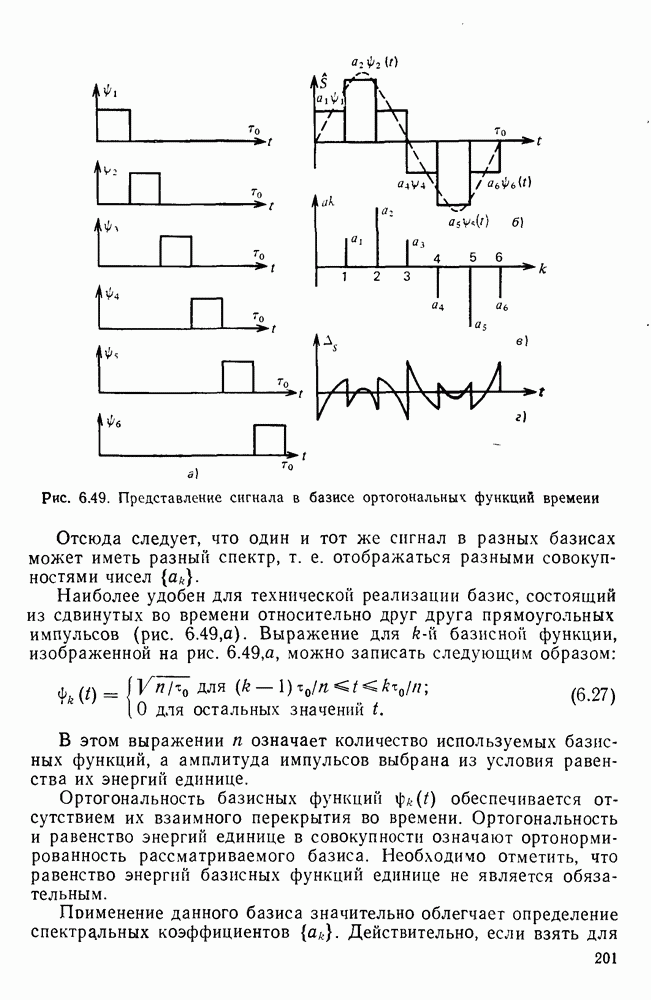
Рис. 6.49. Представление сигнала в базисе ортогональных функций времени
Отсюда следует, что один и тот же сигнал в разных базисах может иметь разный спектр, т. е. отображаться разными совокупностями чисел 
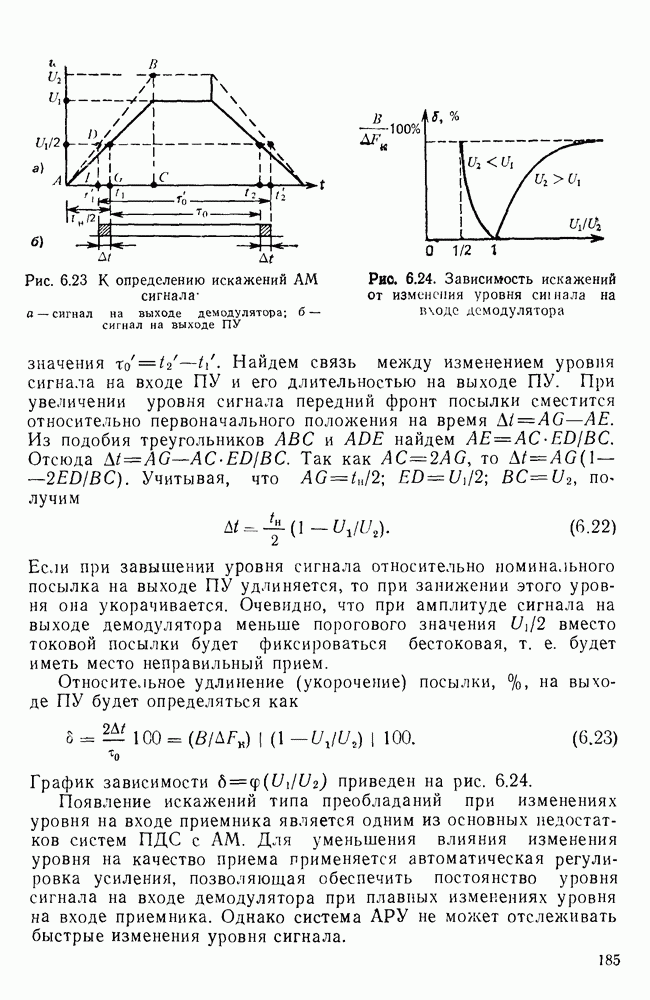
Наиболее удобен для технической реализации базис, состоящий из сдвинутых во времени относительно друг друга прямоугольных импульсов (рис. 6.49, а). Выражение для  базисной функции, изображенной на рис. 6.49, а, можно записать следующим образом:
базисной функции, изображенной на рис. 6.49, а, можно записать следующим образом:

[О для остальных значений 
В этом выражении  означает количество используемых базисных функций, а амплитуда импульсов выбрана из условия равенства их энергий единице.
означает количество используемых базисных функций, а амплитуда импульсов выбрана из условия равенства их энергий единице.
Ортогональность базисных функций обеспечивается отсутствием их взаимного перекрытия во времени. Ортогональность и равенство энергий единице в совокупности означают ортонормированность рассматриваемого базиса. Необходимо отметить, что равенство энергий базисных функций единице не является обязательным.
Применение данного базиса значительно облегчает определение спектральных коэффициентов 

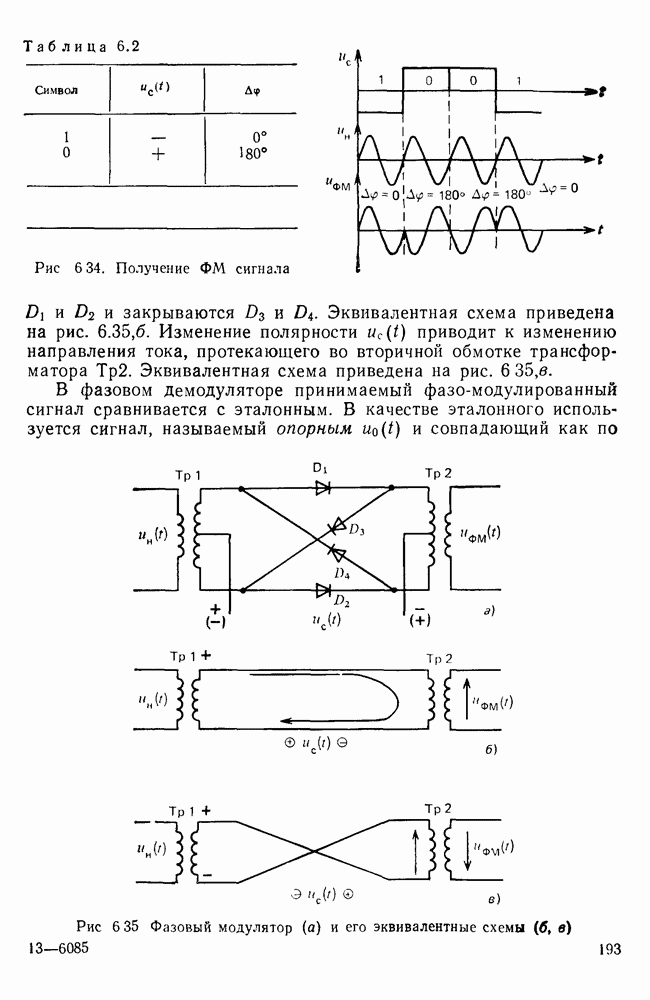
Рис. 6 50 Схема трансверсального фильтра
Действительно, если взять для простоты амплитуды функций  равными единице, то с учетом того, что базисные функции равны нулю вне интервала
равными единице, то с учетом того, что базисные функции равны нулю вне интервала  выражение (6.26) существенно упрощается:
выражение (6.26) существенно упрощается:

Таким образом, для вычисления  необходим лишь интегратор. Совокупность спектральных коэффициентов для синусоидального сигнала в рассматриваемом базисе изображена на рис. 6.49, б.
необходим лишь интегратор. Совокупность спектральных коэффициентов для синусоидального сигнала в рассматриваемом базисе изображена на рис. 6.49, б.
С помощью таких базисных функций также легко и генерировать (синтезировать) сигналы. На рис.  показано представление синусоидального сигнала суммой сдвинутых во времени импульсов, взятых с весовыми коэффициентами
показано представление синусоидального сигнала суммой сдвинутых во времени импульсов, взятых с весовыми коэффициентами  , а на рис. 6.50 изображена схема для генерации таким способом синусоидального сигнала. Схема содержит регистр сдвига, содержащий
, а на рис. 6.50 изображена схема для генерации таким способом синусоидального сигнала. Схема содержит регистр сдвига, содержащий  ячеек памяти. Если на тактовые входы ячеек памяти подавать тактовые импульсы с частотой
ячеек памяти. Если на тактовые входы ячеек памяти подавать тактовые импульсы с частотой  то при продвижении импульса, записанного предварительно в первую ячейку, на выходах ячеек памяти будут последовательно во времени возникать импульсы длительностью
то при продвижении импульса, записанного предварительно в первую ячейку, на выходах ячеек памяти будут последовательно во времени возникать импульсы длительностью 
Таким образом, регистр сдвига можно рассматривать как генератор базисных функций  Для придания импульсам амплитуд, определяемых значениями соответствующих спектральных коэффициентов (рис. 6.49, б), обычно применяют делители напряжений, образованные резисторами
Для придания импульсам амплитуд, определяемых значениями соответствующих спектральных коэффициентов (рис. 6.49, б), обычно применяют делители напряжений, образованные резисторами  и общим резистором
и общим резистором  Очевидно, что коэффициенты деления делителей должны быть равны (или пропорциональны) значениям
Очевидно, что коэффициенты деления делителей должны быть равны (или пропорциональны) значениям 
Так как резистивные делители не могут изменять знак напряжения, то к выходам последних трех ячеек регистра сдвига подключены инверторы  знака базисных функций. Схема, изображенная на рис. 6.50, несмотря на простоту, обладает широкими возможностями.
знака базисных функций. Схема, изображенная на рис. 6.50, несмотря на простоту, обладает широкими возможностями.
Так, например, соединив выход последней и вход первой ячейки памяти, можно получить синусоидальный сигнал, состоящий из любого числа периодов. Изменяя место записи исходного импульса, можно осуществлять фазовую модуляцию. После некоторого усложнения данная схема может быть использована и в качестве частотного модулятора.
Схему, изображенную на рис. 6.50, часто называют трансверсалъным фильтром. Такое название обусловлено тем, что эту схему можно рассматривать и как схему фильтра с импульсной реакцией, имеющей форму ступенчатой функции  изображенной на рис. 6.49,б. Путем подбора коэффициентов деления делителей напряжения легко можно получить фильтр с практически любой дискретной во времени импульсной реакцией. Сигнал, подлежащий фильтрации, подается на вход регистра сдвига. Разумеется, при фильтрации аналоговых сигналов ячейки памяти регистра должны позволять хранить отсчеты аналоговых сигналов.
изображенной на рис. 6.49,б. Путем подбора коэффициентов деления делителей напряжения легко можно получить фильтр с практически любой дискретной во времени импульсной реакцией. Сигнал, подлежащий фильтрации, подается на вход регистра сдвига. Разумеется, при фильтрации аналоговых сигналов ячейки памяти регистра должны позволять хранить отсчеты аналоговых сигналов.
На рис. 6.49, г показана погрешность  представления сигнала
представления сигнала  в рассматриваемом базисе. Очевидно, что чем меньше длительность прямоугольных импульсов, аппроксимирующих сигнал
в рассматриваемом базисе. Очевидно, что чем меньше длительность прямоугольных импульсов, аппроксимирующих сигнал  , а следовательно, больше их число, тем точнее можно отобразить сигнал в выбранном базисе.
, а следовательно, больше их число, тем точнее можно отобразить сигнал в выбранном базисе.
В системах ПДС находят применение и другие базисные функции, например Уолша. Целесообразность применения той или иной системы функций определяется разработчиками аппаратуры, исходя из конкретных условий работы системы ПДС или ограничений на сложность ее реализации.
Итак, сигналы с амплитудной, частотной и фазовой модуляцией, как, впрочем, и любые другие аналоговые сигналы, на интервале то могут быть однозначно представлены вместо непрерывных функций времени своими спектральными коэффициентами  т. е. между сигналами и их спектрами в выбранном базисе существует взаимно-однозначное соответствие. Это обстоятельство весьма важно, поскольку представление сигналов их спектральными коэффициентами
т. е. между сигналами и их спектрами в выбранном базисе существует взаимно-однозначное соответствие. Это обстоятельство весьма важно, поскольку представление сигналов их спектральными коэффициентами  дает возможность амплитудную, частотную и фазовую модуляции сигналов на передающей стороне и демодуляцию на приемной стороне заменить соответствующими операциями над числами
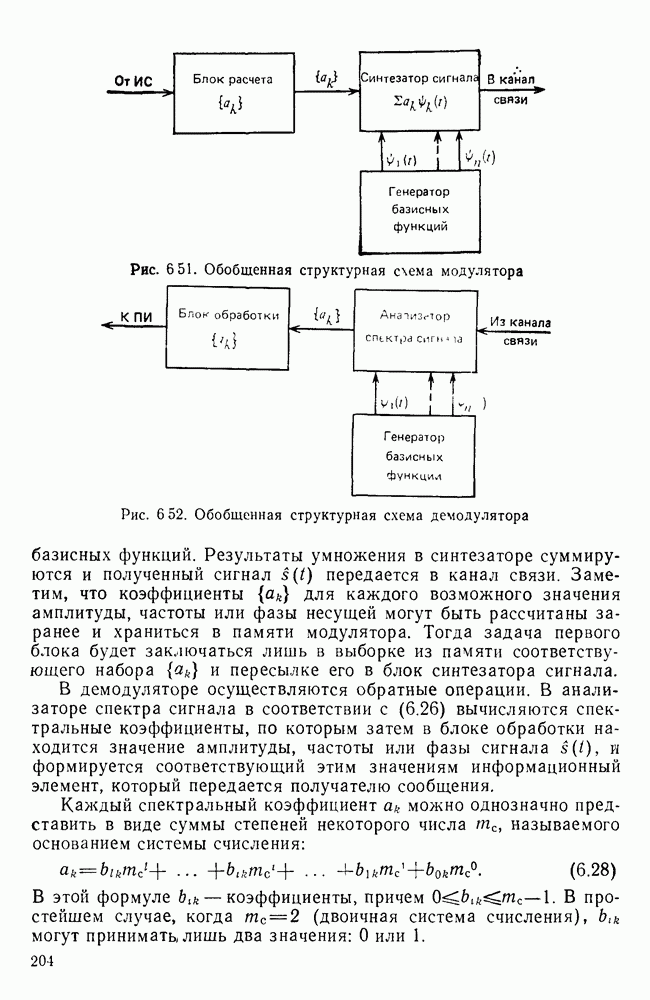
дает возможность амплитудную, частотную и фазовую модуляции сигналов на передающей стороне и демодуляцию на приемной стороне заменить соответствующими операциями над числами  Обобщенные структурные схемы таких модуляторов и демодуляторов приведены соответственно на рис. 6.51 и 6.52.
Обобщенные структурные схемы таких модуляторов и демодуляторов приведены соответственно на рис. 6.51 и 6.52.
В первом блоке модулятора с учетом поступившего от источника сообщения информационного элемента и используемого вида модуляции осуществляется расчет спектральных коэффициентов  с тем, чтобы во втором блоке — синтезаторе сигнала — с их помощью получить канальный сигнал с соответствующей амплитудой, частотой или фазой.
с тем, чтобы во втором блоке — синтезаторе сигнала — с их помощью получить канальный сигнал с соответствующей амплитудой, частотой или фазой.
В синтезаторе сигнала рассчитанные коэффициенты  умножаются на базисные функции
умножаются на базисные функции  которые генерирует генератор базисных функций.
которые генерирует генератор базисных функций.

Рис. 6 51. Обобщенная структурная схема модулятора

Рис. 6 52. Обобщенная структурная схема демодулятора
Результаты умножения в синтезаторе суммируются и полученный сигнал  передается в канал связи. Заметим, что коэффициенты
передается в канал связи. Заметим, что коэффициенты  для каждого возможного значения амплитуды, частоты или фазы несущей могут быть рассчитаны заранее и храниться в памяти модулятора. Тогда задача первого блока будет заключаться лишь в выборке из памяти соответствующего набора
для каждого возможного значения амплитуды, частоты или фазы несущей могут быть рассчитаны заранее и храниться в памяти модулятора. Тогда задача первого блока будет заключаться лишь в выборке из памяти соответствующего набора  и пересылке его в блок синтезатора сигнала.
и пересылке его в блок синтезатора сигнала.
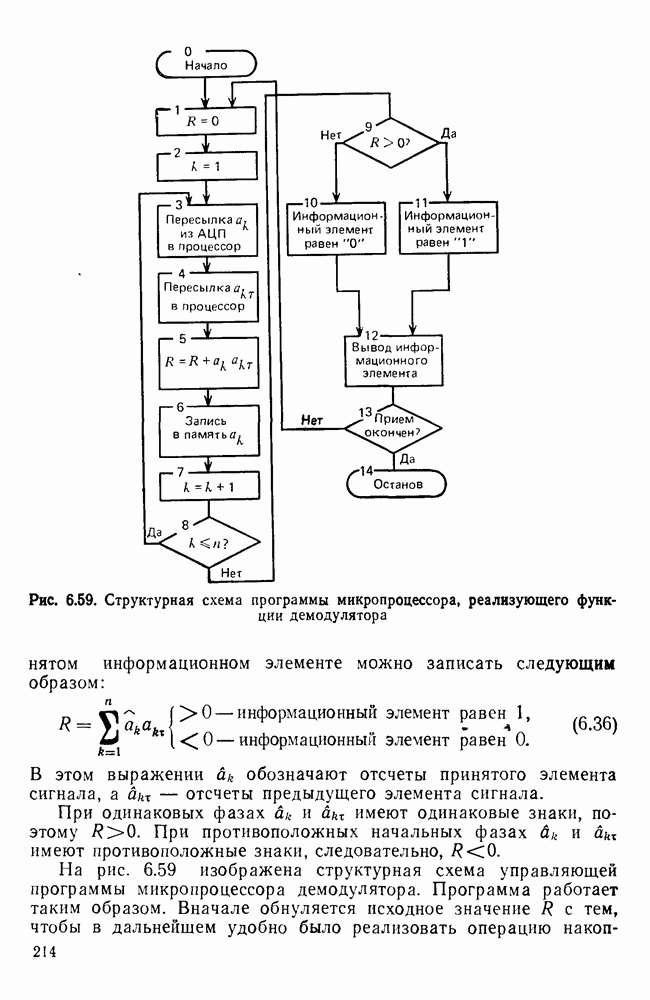
В демодуляторе осуществляются обратные операции. В анализаторе спектра сигнала в соответствии с (6.26) вычисляются спектральные коэффициенты, по которым затем в блоке обработки находится значение амплитуды, частоты или фазы сигнала  и формируется соответствующий этим значениям информационный элемент, который передается получателю сообщения.
и формируется соответствующий этим значениям информационный элемент, который передается получателю сообщения.
Каждый спектральный коэффициент  можно однозначно представить в виде суммы степеней некоторого числа
можно однозначно представить в виде суммы степеней некоторого числа  называемого основанием системы счисления:
называемого основанием системы счисления:

В этой формуле  — коэффициенты, причем
— коэффициенты, причем  . В простейшем случае, когда
. В простейшем случае, когда  (двоичная система счисления),
(двоичная система счисления),  могут принимать, лишь два значения: 0 или 1.
могут принимать, лишь два значения: 0 или 1.
Таблица 6.4

Таким образом, сами  могут быть представлены совокупностью коэффициентов
могут быть представлены совокупностью коэффициентов  которые образуют
которые образуют  -ичные числа (при
-ичные числа (при  — двоичные числа). Для обозначения знака числа вводят дополнительный знаковый разряд перед старшим разрядом
— двоичные числа). Для обозначения знака числа вводят дополнительный знаковый разряд перед старшим разрядом  -ичного числа. Обычно он равен
-ичного числа. Обычно он равен  для положительных чисел и «1» — для отрицательных.
для положительных чисел и «1» — для отрицательных.
В качестве примера в табл. 6.4 записаны двоичные числа, отображающие спектральные коэффициенты синусоидального сигнала для рис.  в базисе функций, представляющих собой сдвинутые во времени прямоугольные импульсы.
в базисе функций, представляющих собой сдвинутые во времени прямоугольные импульсы.
Итак, сигналы, используемые в системах ПДС, могут быть отображены множеством двоичных чисел, а преобразования сигналов в процессе модуляции и демодуляции произведены путем соответствующих операций над двоичными числами, что технически легко осуществляется цифровыми элементами. Формирование и обработка сигналов на основе их отображения совокупностью чисел называются соответственно цифровой генерацией и цифровой обработкой. Устройства, реализующие такие операции, для краткости в дальнейшем именуемые устройствами цифровой обработки сигналов (ЦОС), имеют существенные преимущества по сравнению с устройствами аналоговой обработки и формирования сигналов.
1. Характеристики устройства ЦОС не изменяются при изменении внешних условий (температуры, влажности и т. д.). Это объясняется тем, что устройства ЦОС реализуются на базе цифровых элементов, устойчиво работающих при изменении внешних условий.
2 Возможна реализация ряда операций обработки сигналов, принципиально не реализуемых на базе аналоговых элементов Так, устройства ЦОС могут реализовать алгоритмы обработки сигналов, требующих большое время хранения отсчетов сигнала, поскольку длительность хранения информации цифровыми элементами практически неограниченна
3. Устройства ЦОС удобно изготавливать в виде больших и сверхбольших интегральных схем, в частности, в виде базовых кристаллов или на базе микропроцессоров Это позволяет существенно уменьшить стоимость изготовления УПС.
4. Реализация устройств ЦОС на базе микропроцессоров дает возможность легко изменять алгоритмы генерации и обработки сигналов путем изменения лишь управляющей программы микропроцессора. Это обстоятельство весьма существенно при построении адаптивных систем передачи информации.
Помимо перечисленных возможностей, которые возникают при цифровом представлении сигналов, следует отметить еще и принципиальную возможность относительно простого применения при цифровом формировании и фильтрации сигналов методов помехоустойчивого кодирования. Действительно, результат искажения помехами спектральных коэффициентов сигнала можно рассматривать как искажение некоторых разрядов в двоичных числах, отображающих спектральные коэффициенты сигнала при прохождении им канала связи. Если для цифрового отображения спектральных коэффициентов использовать кодовые комбинации некоторого помехоустойчивого кода, то проблему фильтрации сигнала от помех можно рассматривать как процедуру обнаружения и исправления искаженных разрядов двоичных чисел, отображающих спектральные коэффициенты сигнала на входе приемника.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
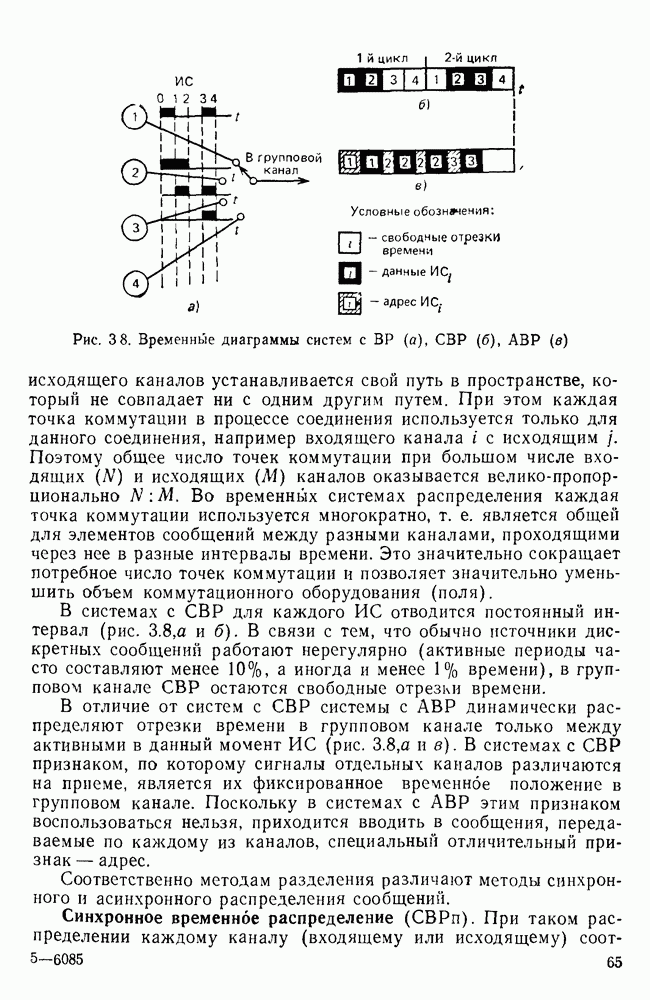
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
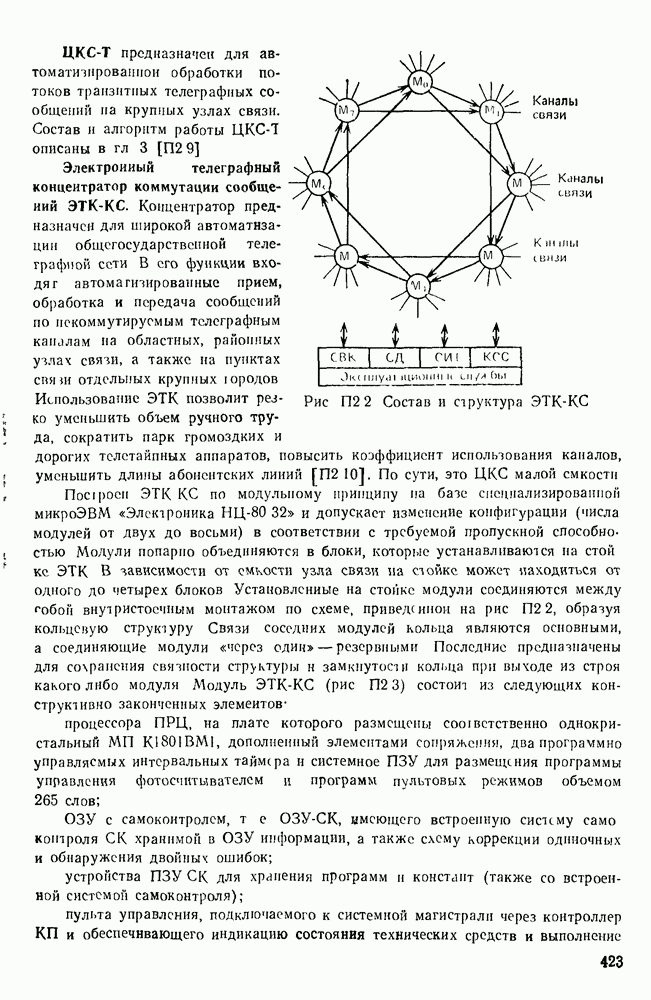
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
- Модулированные сигналы.
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
- Основы микропроцессорной реализации модуляторов УПС.
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
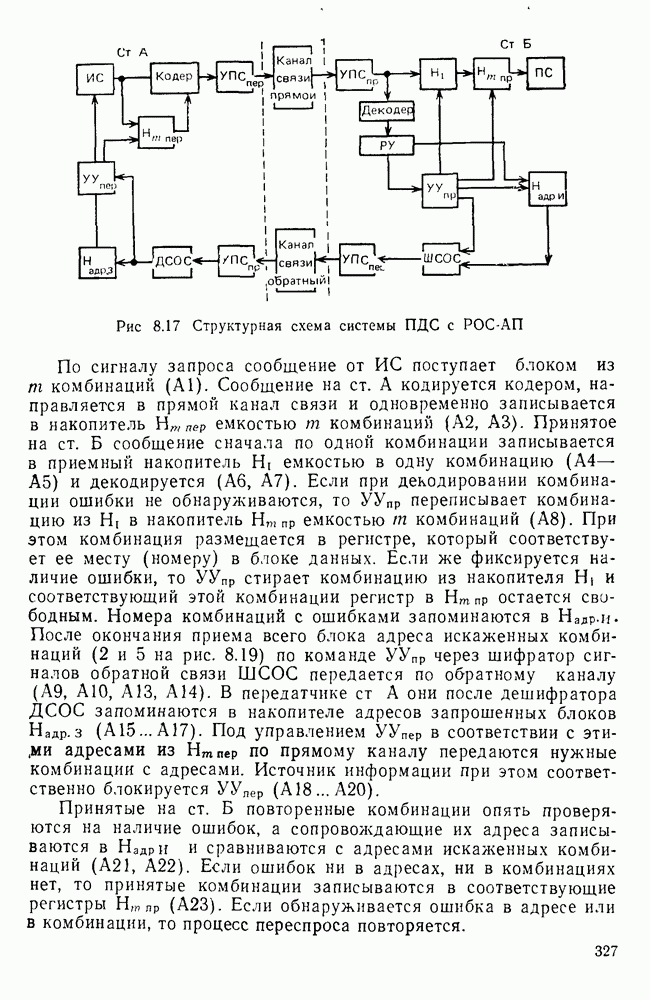
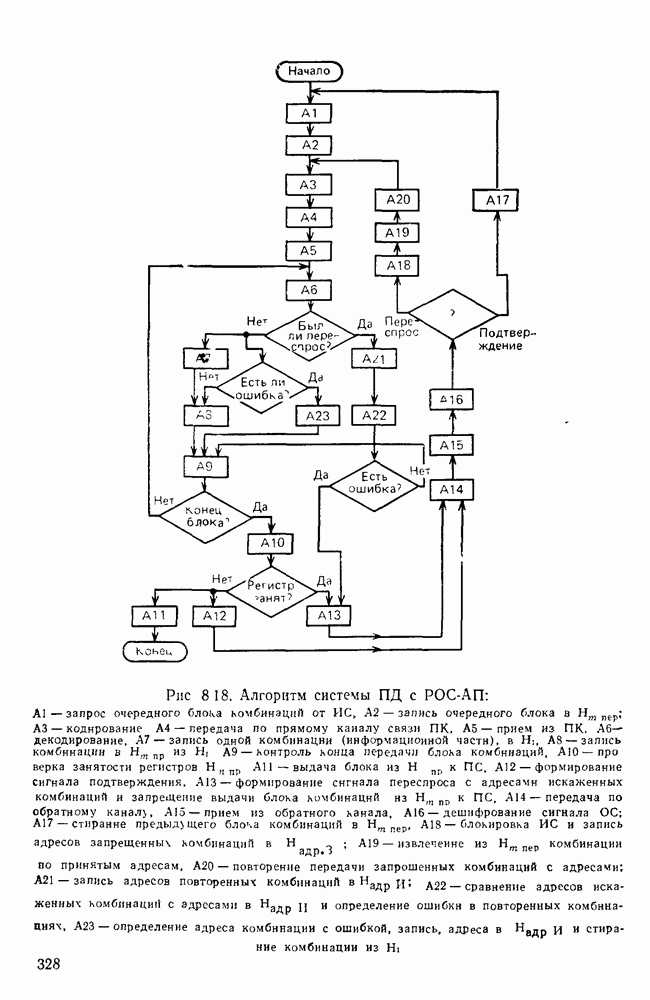
- Система с РОС и адресным переспросом РОС-АП.
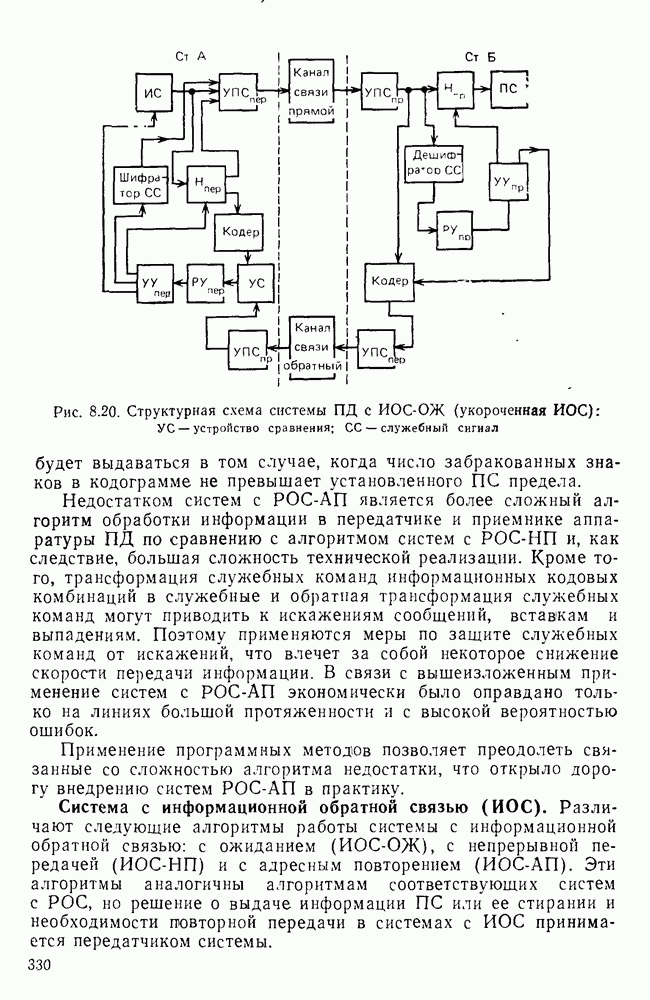
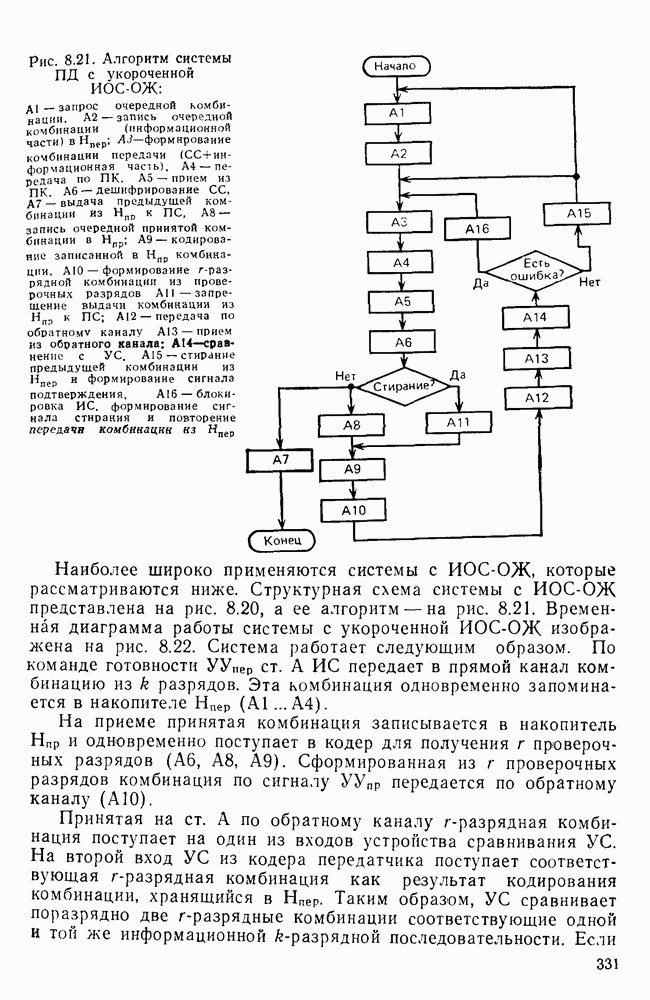
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
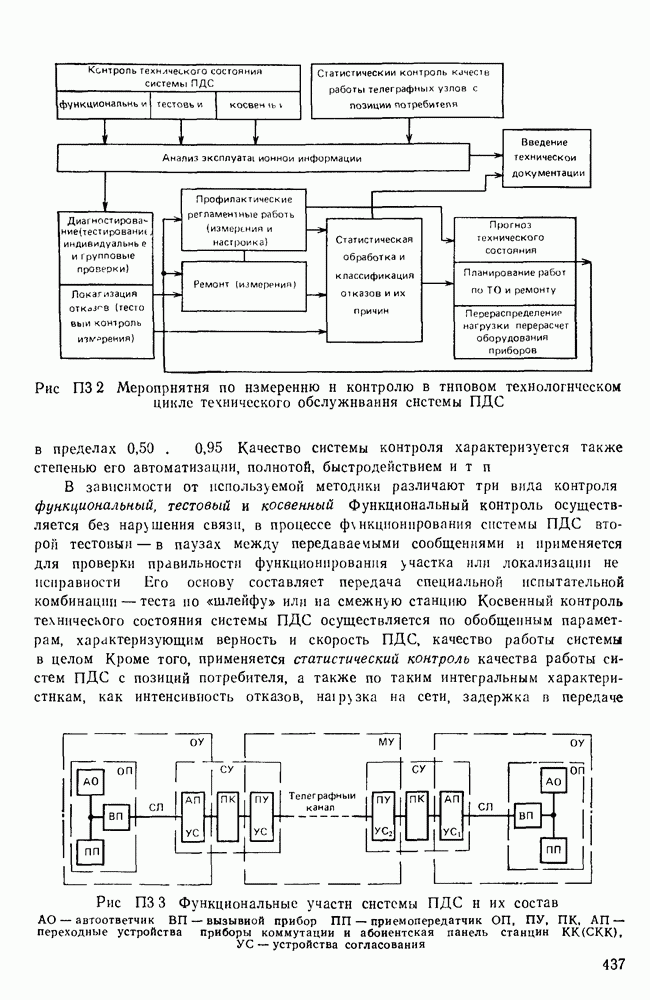
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ