| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
Коды, экономичные одновременно для некоторого класса источников, называют универсальными кодами. Сформулируем постановку задачи универсального кодирования источников Предположим, что алфавит состоит из двух букв  появляющихся независимо с вероятностями
появляющихся независимо с вероятностями  Однако величина
Однако величина  заранее неизвестна. Требуется построить код, для которого среднее число символов «0» и «1» на одну букву алфавита приближалось бы к
заранее неизвестна. Требуется построить код, для которого среднее число символов «0» и «1» на одну букву алфавита приближалось бы к  при любом
при любом  Этот код строится так Множество всех блоков длины
Этот код строится так Множество всех блоков длины  в алфавите А разбиваем на группы, которые имеют одинаковые вероятности при любом
в алфавите А разбиваем на группы, которые имеют одинаковые вероятности при любом  . Таких групп будет ровно
. Таких групп будет ровно  . В нулевой группе отсутствует буква
. В нулевой группе отсутствует буква  она состоит из единственного блока
она состоит из единственного блока  вероятность появления которого
вероятность появления которого  Первая группа состоит из всех блоков длины
Первая группа состоит из всех блоков длины  , содержащих одну букву
, содержащих одну букву  Эта группа состоит из
Эта группа состоит из  блоков, вероятность каждого из которых равна
блоков, вероятность каждого из которых равна  Группа с номером k состоит из всех блоков длины
Группа с номером k состоит из всех блоков длины  , содержащих k букв
, содержащих k букв  Эта группа содержит
Эта группа содержит  блоков, вероятность каждого из которых
блоков, вероятность каждого из которых 
Универсальный код для  группы состоит из двух частей: префикса и суффикса. Префикс содержит
группы состоит из двух частей: префикса и суффикса. Префикс содержит  двоичных знаков. Префикс указывает, к какой группе сообщений принадлежит кодируемый блок, суффикс содержит
двоичных знаков. Префикс указывает, к какой группе сообщений принадлежит кодируемый блок, суффикс содержит  двоичных символов и указывает номер блока в группе.
двоичных символов и указывает номер блока в группе.
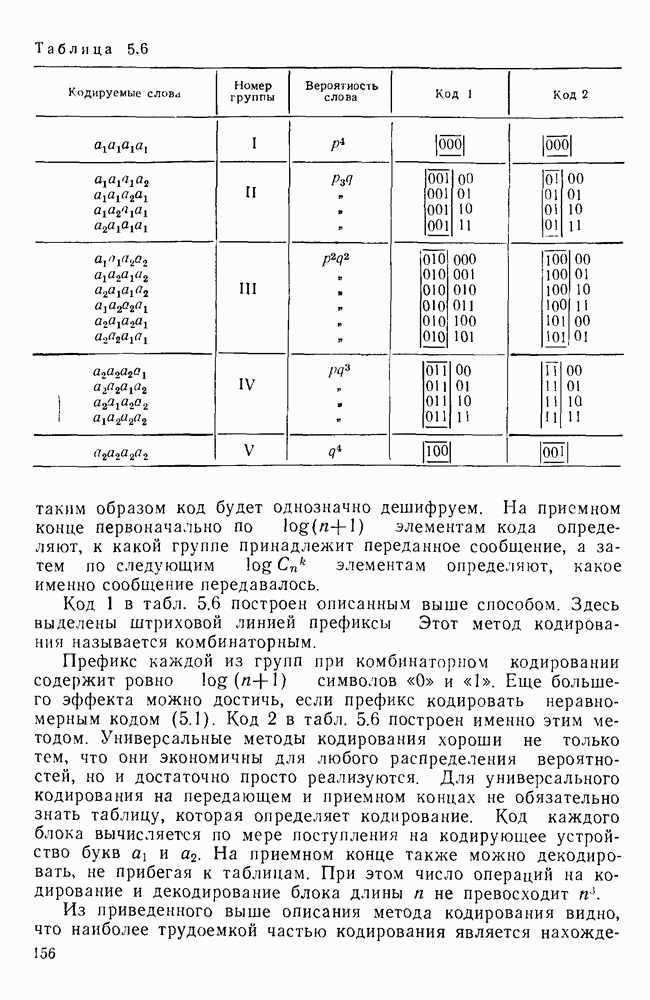
Таблица 5.6

Построенный таким образом код будет однозначно дешифруем. На приемном конце первоначально по  элементам кода определяют, к какой группе принадлежит переданное сообщение, а затем по следующим
элементам кода определяют, к какой группе принадлежит переданное сообщение, а затем по следующим  элементам определяют, какое именно сообщение передавалось.
элементам определяют, какое именно сообщение передавалось.
Код 1 в табл. 5.6 построен описанным выше способом. Здесь выделены штриховой линией префиксы Этот метод кодирования называется комбинаторным.
Префикс каждой из групп при комбинаторном кодировании содержит ровно  символов «0» и «1». Еще большего эффекта можно достичь, если префикс кодировать неравномерным кодом (5.1). Код 2 в табл. 5.6 построен именно этим методом. Универсальные методы кодирования хороши не только тем, что они экономичны для любого распределения вероятностей, но и достаточно просто реализуются. Для универсального кодирования на передающем и приемном концах не обязательно знать таблицу, которая определяет кодирование. Код каждого блока вычисляется по мере поступления на кодирующее устройство букв
символов «0» и «1». Еще большего эффекта можно достичь, если префикс кодировать неравномерным кодом (5.1). Код 2 в табл. 5.6 построен именно этим методом. Универсальные методы кодирования хороши не только тем, что они экономичны для любого распределения вероятностей, но и достаточно просто реализуются. Для универсального кодирования на передающем и приемном концах не обязательно знать таблицу, которая определяет кодирование. Код каждого блока вычисляется по мере поступления на кодирующее устройство букв  На приемном конце также можно декодировать, не прибегая к таблицам. При этом число операций на кодирование и декодирование блока длины
На приемном конце также можно декодировать, не прибегая к таблицам. При этом число операций на кодирование и декодирование блока длины  не превосходит
не превосходит 
Из приведенного выше описания метода кодирования видно, что наиболее трудоемкой частью кодирования является нахождение суффикса.
Опишем алгоритм нахождения суффикса. Пусть в блоке А длины  буква
буква  встречается на местах
встречается на местах  тогда суффиксом для А назовем число
тогда суффиксом для А назовем число  вычисляемое по правилу:
вычисляемое по правилу:

Очевидно, что блоки с разными наборами получают разные номера. При этом максимальное значение номера равно

Таким образом, двоичная запись номера (суффикса) должна иметь длину  Для нахождения
Для нахождения  воспользуемся таблицей биноминальных коэффициентов (треугольником Паскаля):
воспользуемся таблицей биноминальных коэффициентов (треугольником Паскаля):

Элементы этой таблицы вычисляются по мере надобности либо размещаются в памяти кодирующего устройства. Приведем фрагмент этой таблицы, в которой на пересечении  строки и
строки и  столбца стоит
столбца стоит 
Пример 5.3. Пусть  тогда
тогда  Тогда номер блока
Тогда номер блока  Слагаемые к N(А) находим, используя таблицу дополнительных коэффициентов
Слагаемые к N(А) находим, используя таблицу дополнительных коэффициентов  выделены жирным шрифтом Таким образом,
выделены жирным шрифтом Таким образом,  или в двоичном записи
или в двоичном записи 
Декодирование производится с помощью этой же таблицы.
Пример 5.4. Пусть нам известно, что длина передаваемого блока равна 8, и что в блоке пять букв  (количество букв в блоке находим по префиксу). Находим максимальное число в
(количество букв в блоке находим по префиксу). Находим максимальное число в  столбце, не превосходящее 32, это
столбце, не превосходящее 32, это  следовательно,
следовательно,  находим разность
находим разность  Находим далее максимальное число
Находим далее максимальное число  столбца, не превосходящее 11. Это
столбца, не превосходящее 11. Это  Аналогично находим
Аналогично находим  Следовательно, декодированное сообщение имеет вид
Следовательно, декодированное сообщение имеет вид

Рассмотренные кодирование и декодирование достаточно просто осуществляются с помощью специализированных вычислительных средств.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
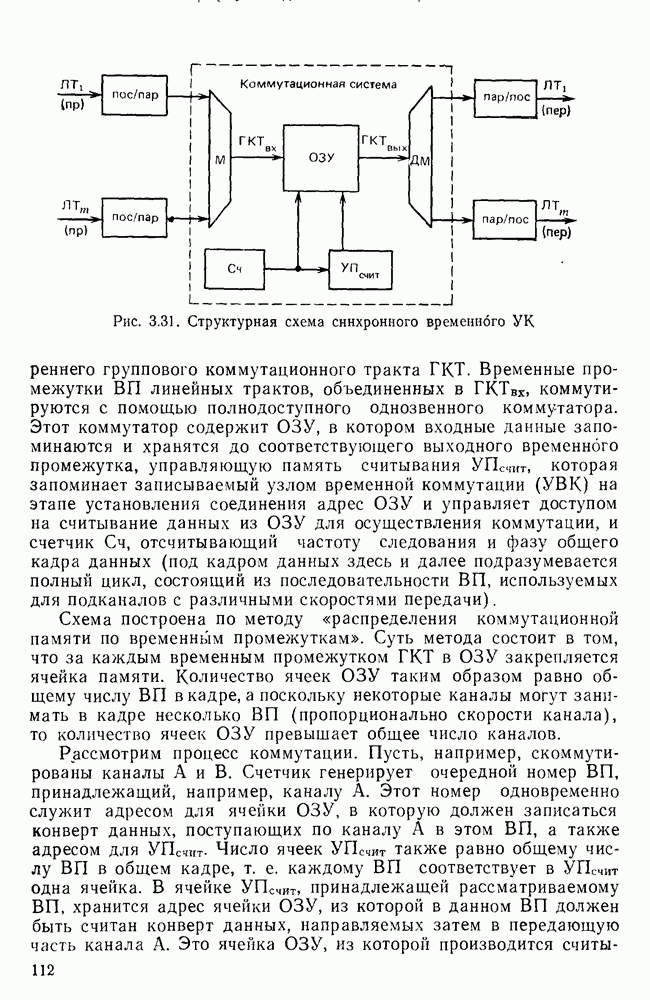
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
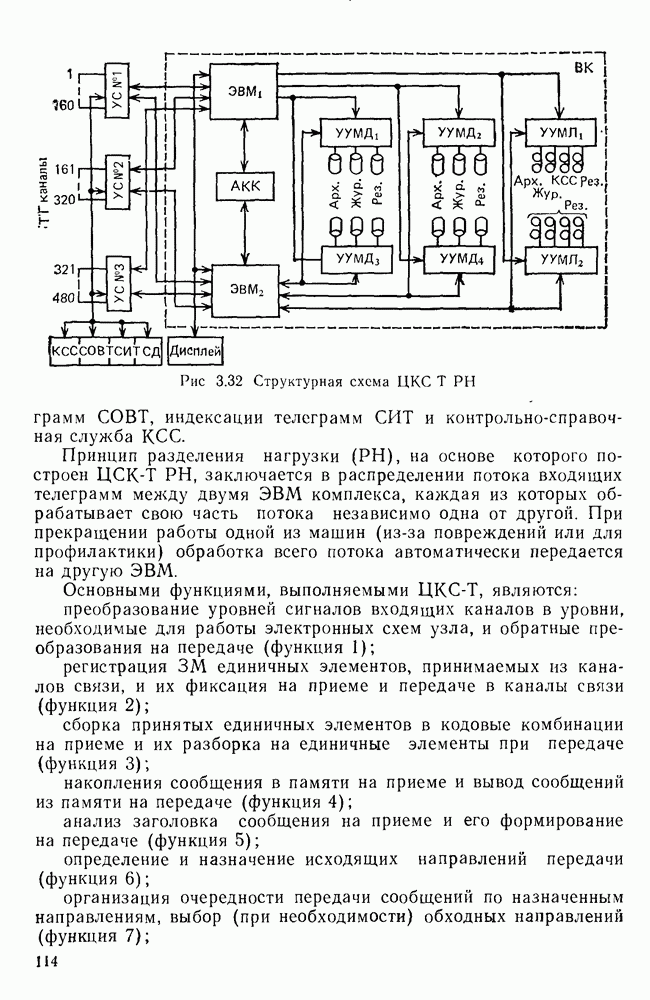
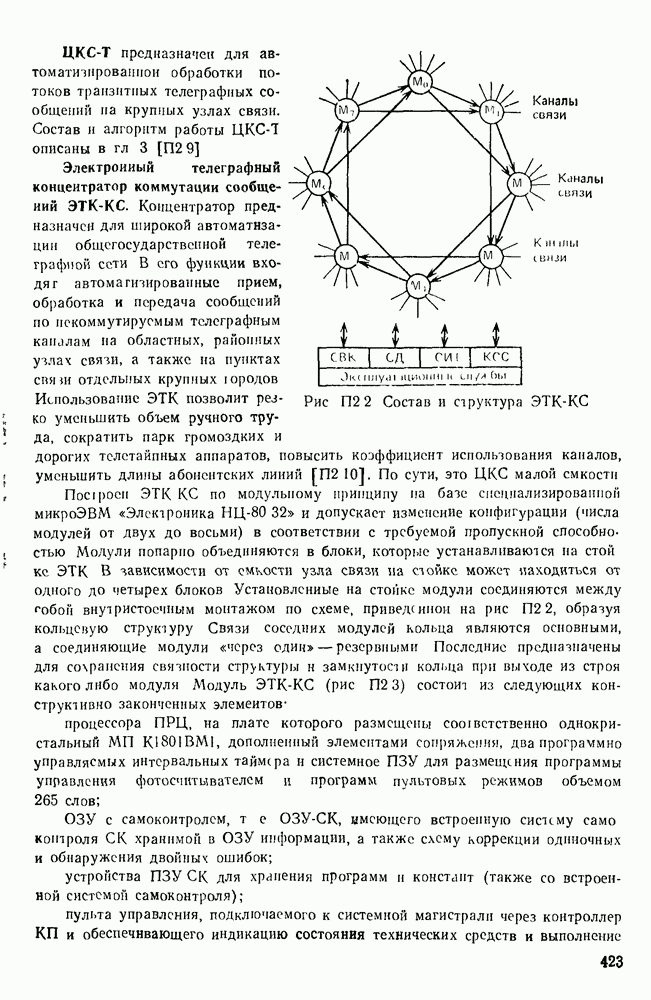
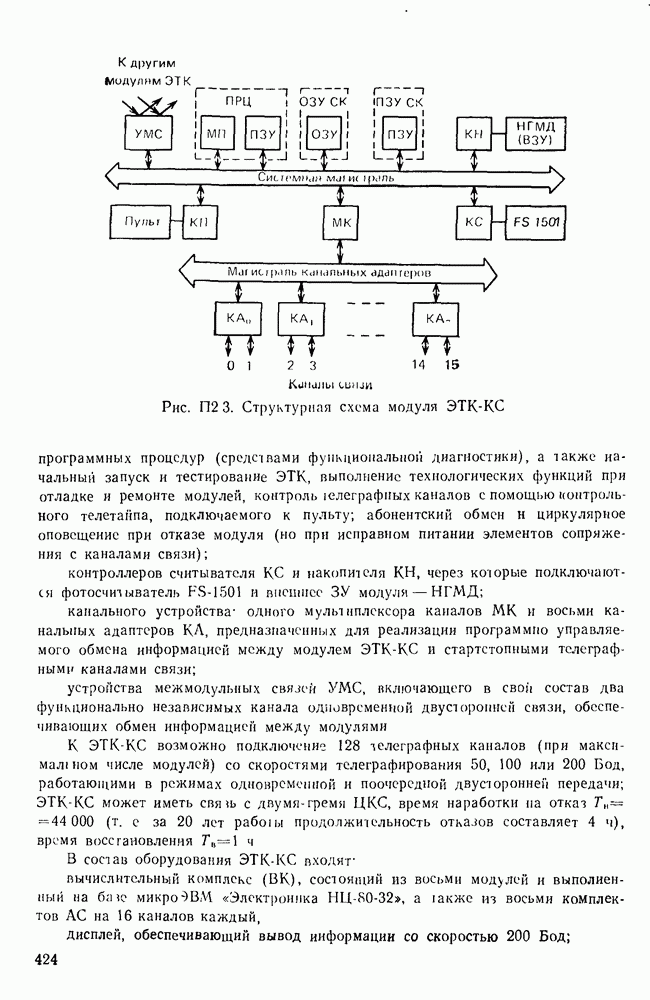
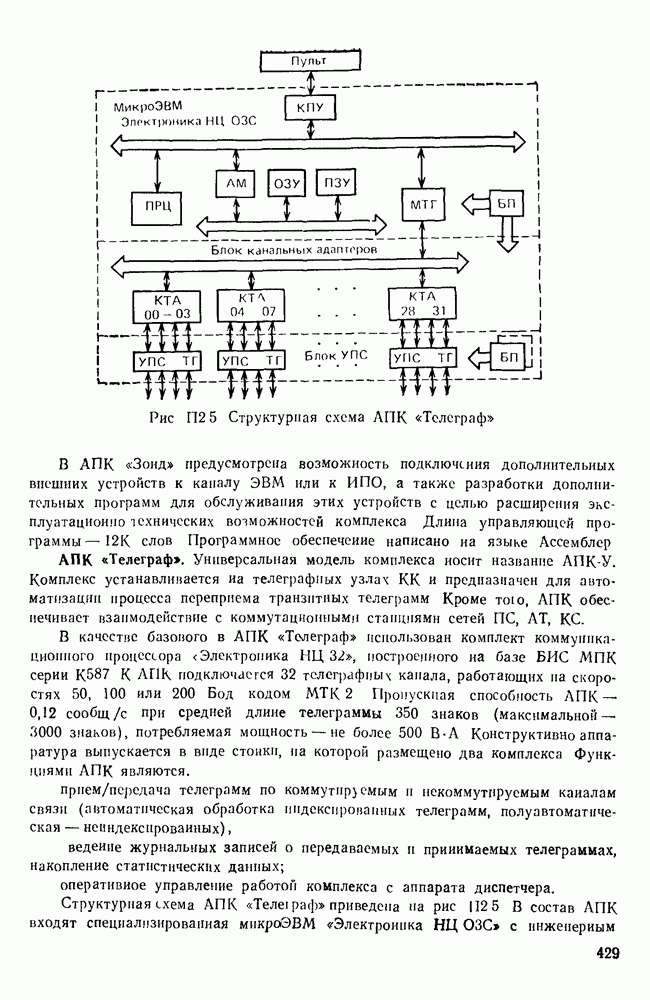
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
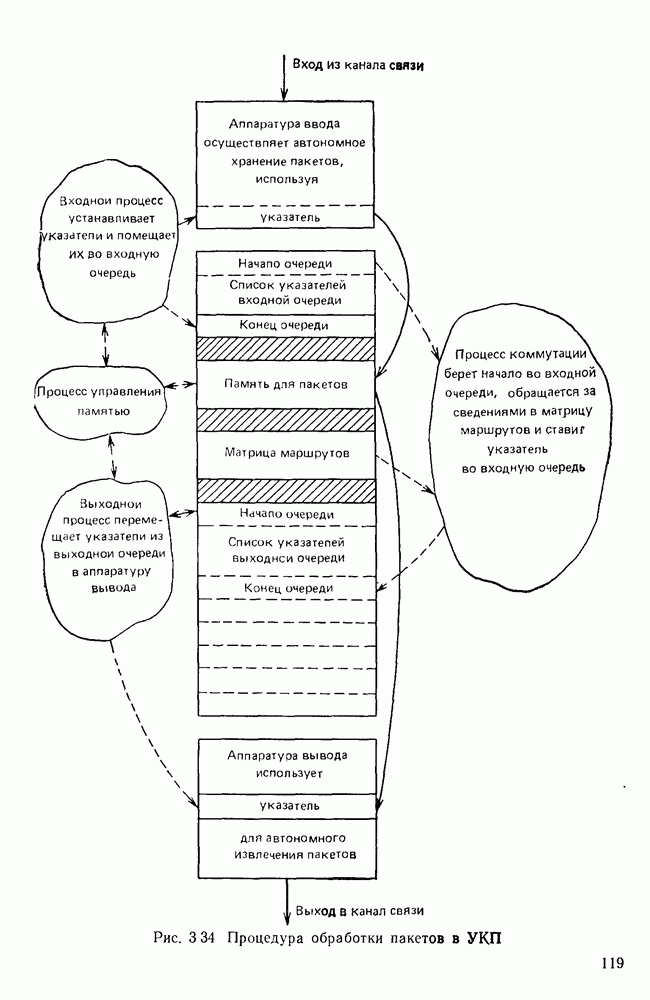
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
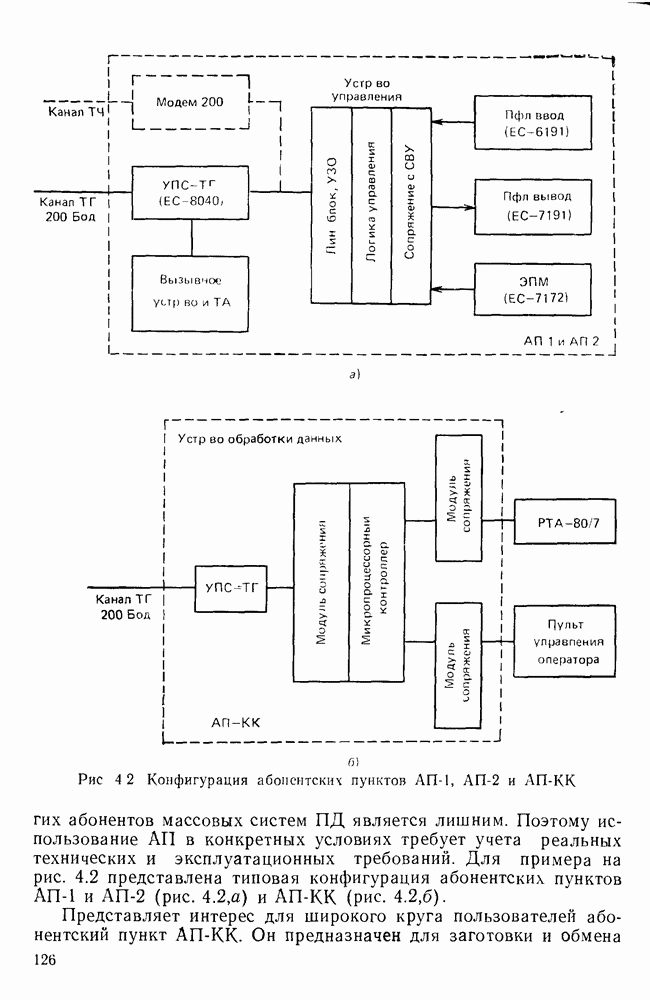
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
- Модулированные сигналы.
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
- Основы микропроцессорной реализации модуляторов УПС.
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
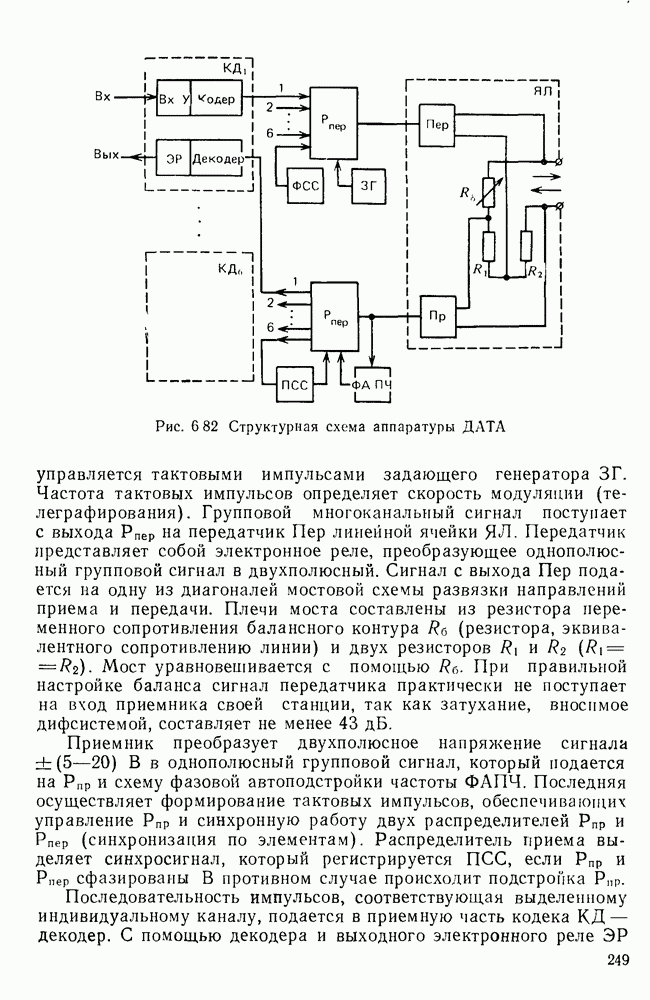
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
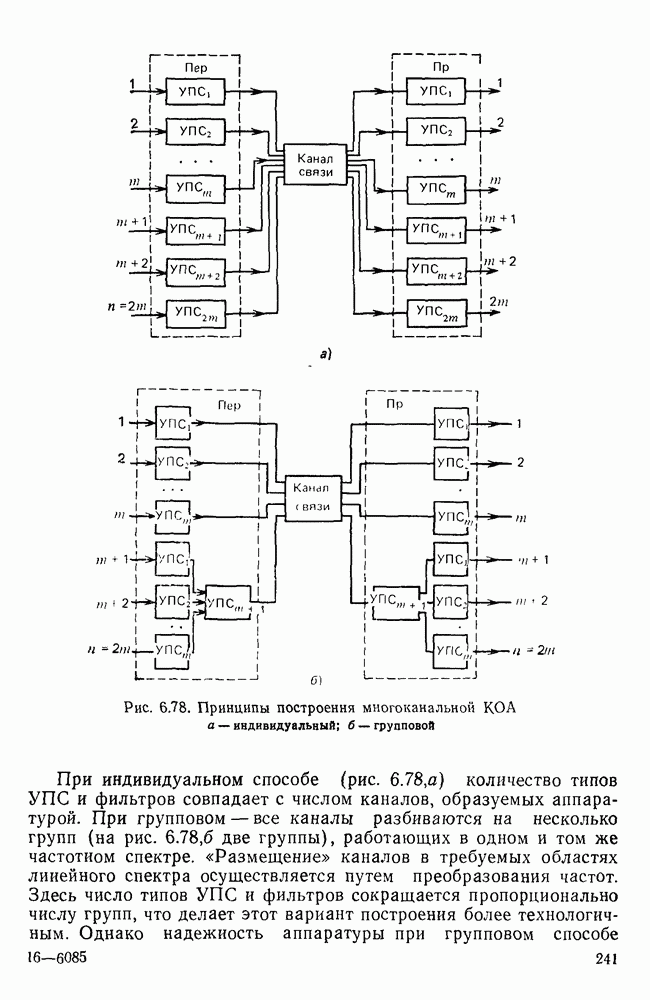
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
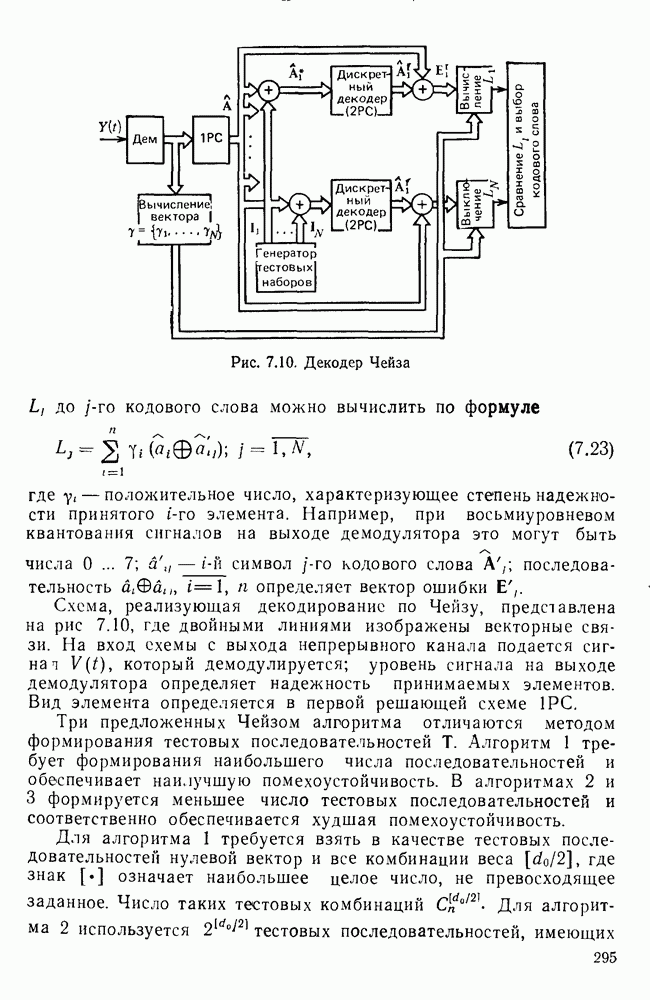
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
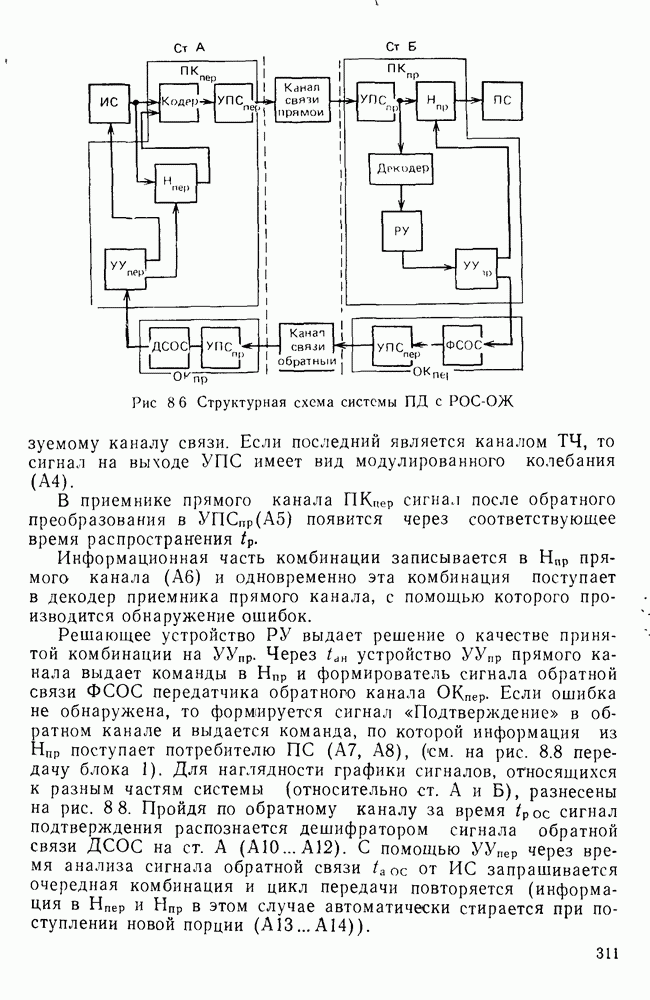
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
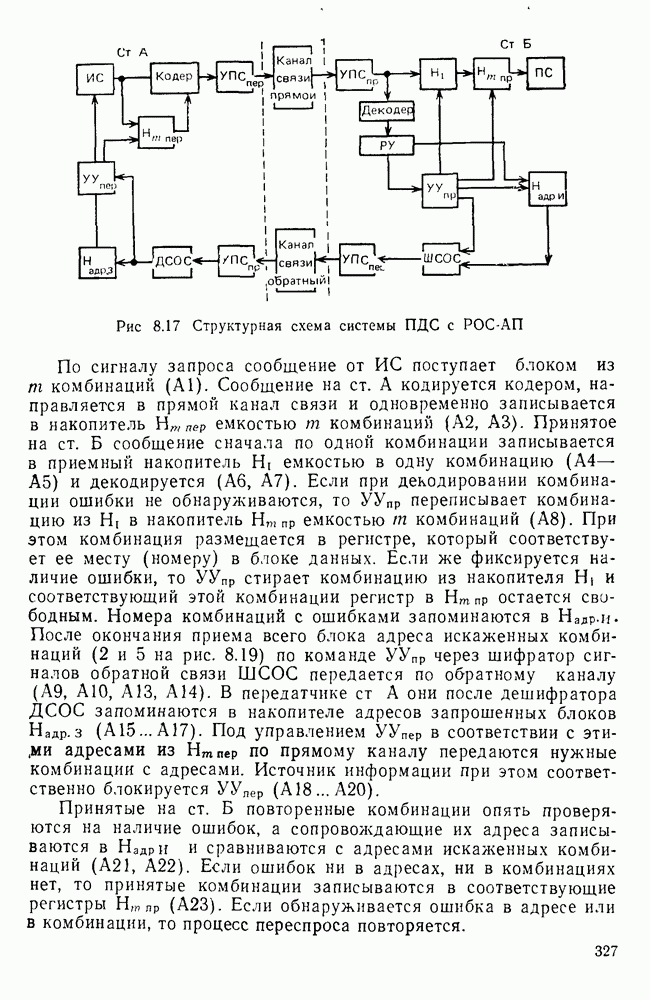
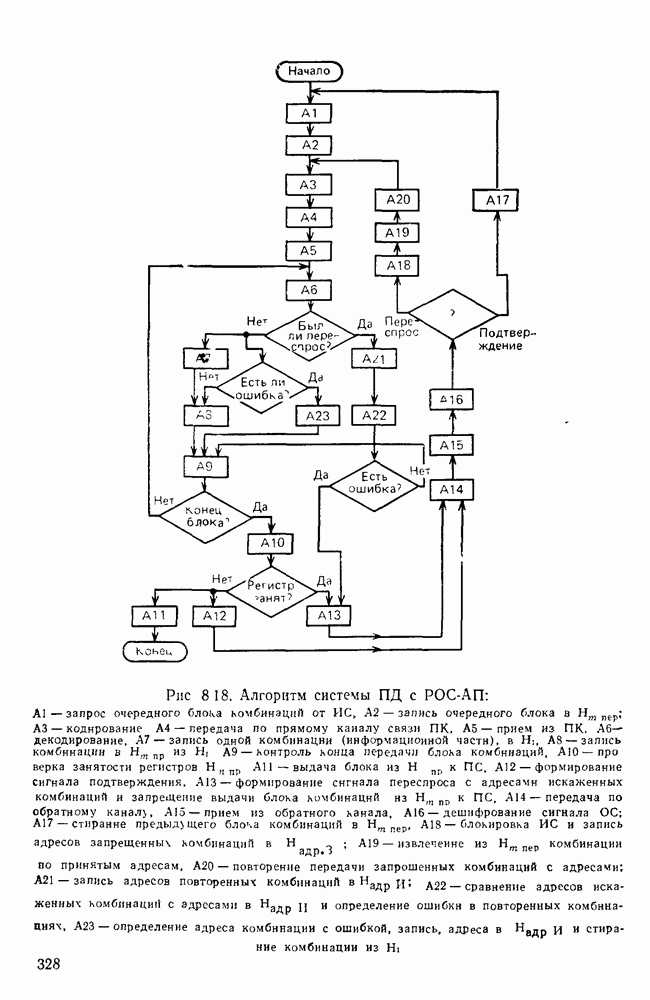
- Система с РОС и адресным переспросом РОС-АП.
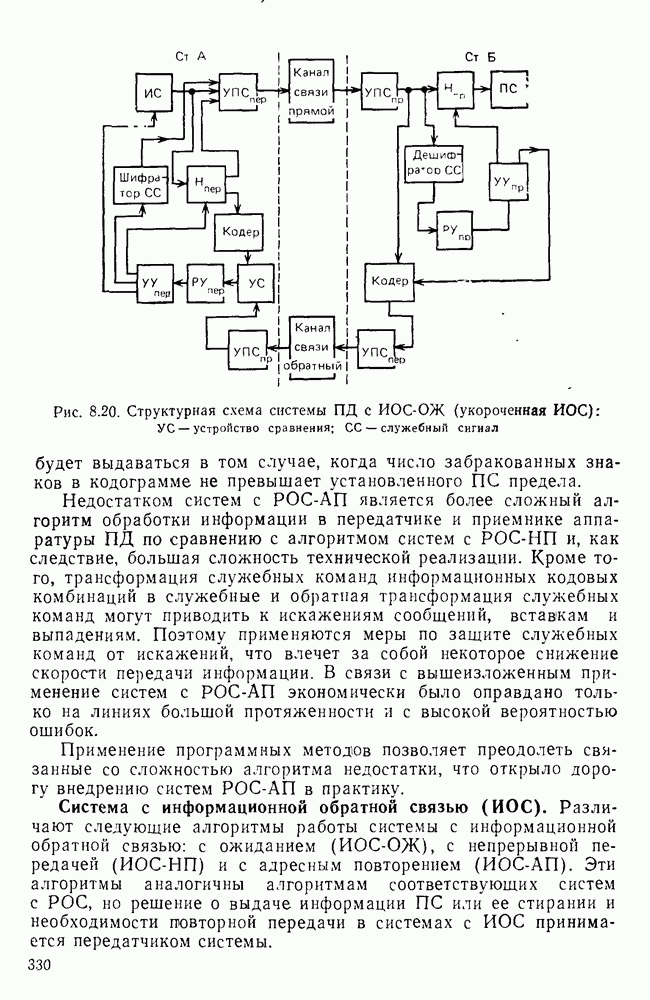
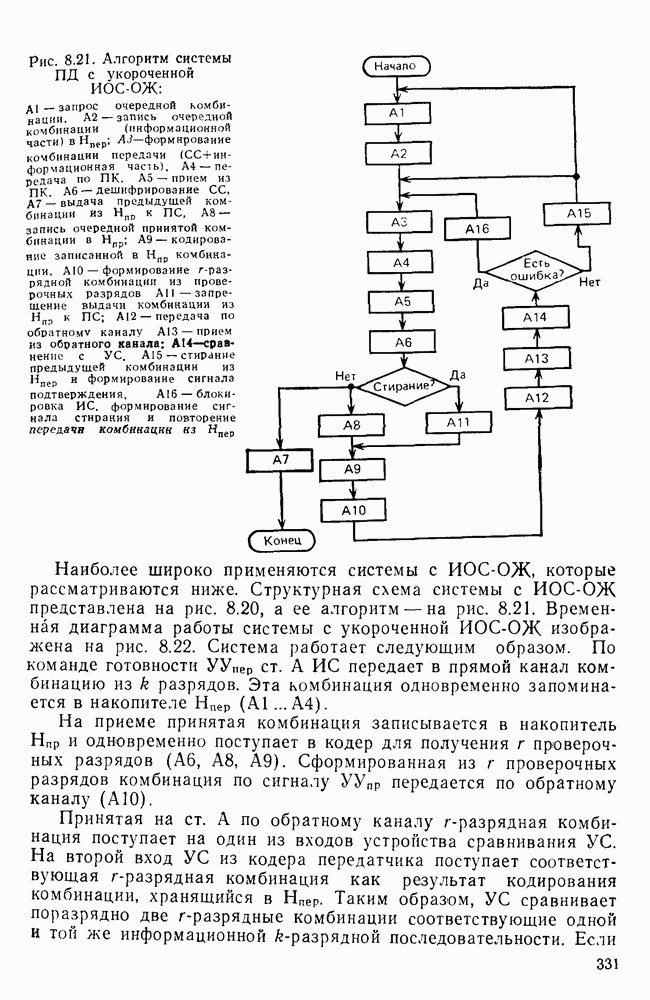
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
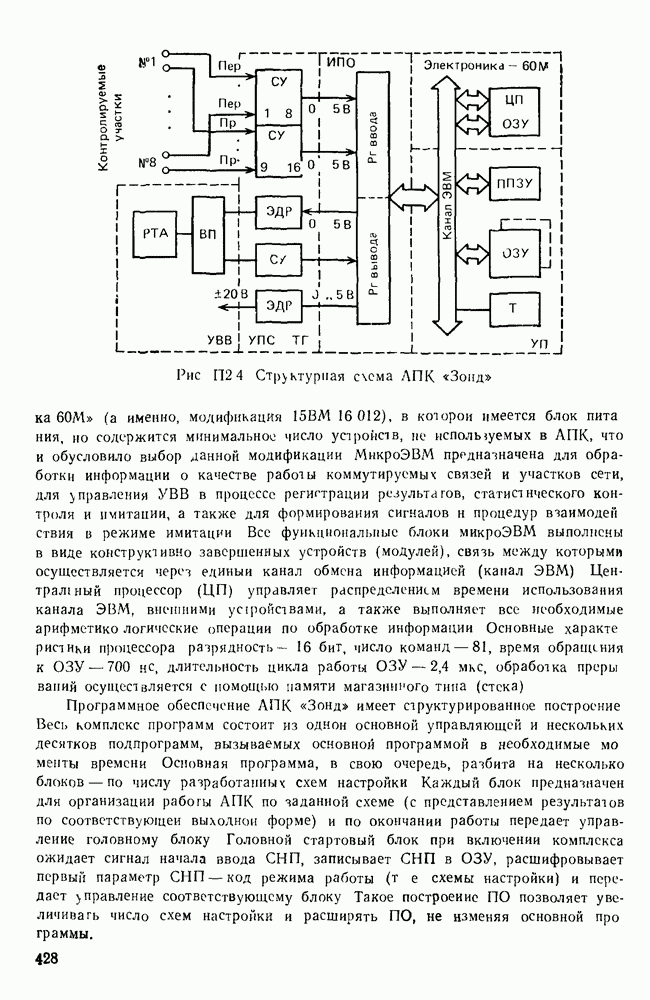
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ