| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
Понятие случайных чисел Для имитации источника сообщения, а также действия различных случайных факторов, сопровождающих процесс передачи сообщений в системе ПДС, при моделировании возникает необходимость формировать реализации случайных событий, величин, процессов.
Исходным материалом для формирования в цифровых вычислительных машинах реализаций, имеющих случайный характер, обычно служат так называемые случайные числа Последние могут быть получены и введены в машину различными способами Например, можио хранить в запоминающих устроиавах ЭВМ специальные таблицы случайных чисел и выбирать из них отдельные числа по мере надобности Однако чаще всего случайные числа вырабатываются в самой машине с помощью специальных программ (датчиков случайных чисел). Однако случайные числа являются лишь исходным материалом для получения реализаций различных случайных процессов, необходимых при моделировании. Существуют различные способы преобразования исходных случайных чисел в реализации случайных процессов с заданными свойствами В качестве исходной совокупности случайных чисел чаще всего используется совокупность случайных чисел с равномерным распределением в интервале (0,1). Такая совокупность получается с небольшими затратами машинного времени и обеспечивает простоту и удобство дальнейших необходимых преобразований.
Моделирование источника сообшения. Задачей программного модуля источника информации, как это отмечалось в разд  является генерация информационных символов «0» или «1», имеющих случайный характер Для большинства двоичных источников сообщений вероятности «0» или «1» примерно равны 0,5.
является генерация информационных символов «0» или «1», имеющих случайный характер Для большинства двоичных источников сообщений вероятности «0» или «1» примерно равны 0,5.
Для получения равновероятных чисел «1» и «0» удобно воспользоваться имеющимися в математическом обеспечении современных ЭВМ стандартными подпрограммами, вырабатывающими при каждом обращении к ним случайное число X с равномерным законом распределения вероятностей в интервале значений от 0 до 1. Можио предложить следующий алгоритм формирования равновероятных информационных символов  или
или  с помощью числа X: если сформированное подпрограммой число
с помощью числа X: если сформированное подпрограммой число  то
то  иначе
иначе 
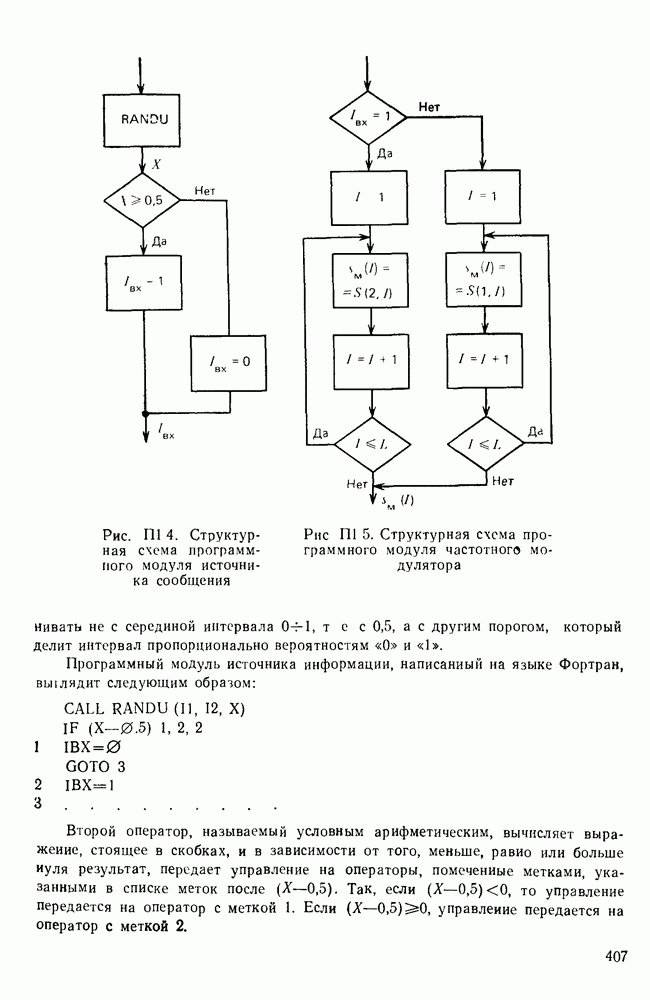
Структурная схема программного модуля источника сообщений, использующего подпрограмму RANDU формирования равномерно распределенных в интервале  чисел, изображена на рис
чисел, изображена на рис  . В языке Фортран обращение к подпрограмме осуществляется оператором CALL RANDU (II, 12, X). Числа целого типа II, 12, равные нулю, выполняют служебные функции. Они должны быть заранее заданы в модуле ввода исходных данных.
. В языке Фортран обращение к подпрограмме осуществляется оператором CALL RANDU (II, 12, X). Числа целого типа II, 12, равные нулю, выполняют служебные функции. Они должны быть заранее заданы в модуле ввода исходных данных.

Рис. П. 1.4. Структурная схема программного модуля источника сообщения

Рис. П. 1.5. Структурная схема программного модуля частотного модулятора
При необходимости формирования неравновероятных символов следует, очевидно, генерируемое число X сравнивать не с серединой интервала  а с другим порогом, который делит интервал пропорционально вероятностям «0» и «1».
а с другим порогом, который делит интервал пропорционально вероятностям «0» и «1».
Программный модуль источника информации, написанный на языке Фортран, вьплядит следующим образом:

Второй оператор, называемый условным арифметическим, вычисляет выражение, стоящее в скобках, и в зависимости от того, меньше, равио или больше нуля результат, передает управление на операторы, помеченные метками, указанными в списке меток после  Так, если
Так, если  то управление передается на оператор с меткой 1. Если
то управление передается на оператор с меткой 1. Если  управление передается на оператор с меткой 2.
управление передается на оператор с меткой 2.
Оператор безусловного перехода GO ТО служит для обхода оператора с меткой 2 с целью сохранения уже полученного значения 
Моделирование передатчика. Задачей модуля передатчика является формирование временных отсчетов сигнала, посылаемого в канал связи В общем случае программный модуль передатчика должен содержать группу операторов, моделирующих работу кодера, и группу операторов, моделирующих работу модулятора В качестве примера рассмотрим реализацию модуля передатчика, использующего частотную модуляцию (помехоустойчивое кодирование не используется)
Согласно соответствующей рекомендации МККТТ информационный элемент, равный нулю, передается гармоническим сигналом с верхней характеристической частотой  а равный единице — с нижней характеристической частотой
а равный единице — с нижней характеристической частотой  т. е.
т. е.

Эти выражения описывают сигналы, непрерывные во времени. ЭВМ может рассчитывать значения сигналов лишь для конкретных значений t, отстоящих друг от друга через определенные интервалы  Величину
Величину  можно рассчитать с помощью теоремы Котельникова, выбрав в качестве верхней частоты спектра сшнала, например, верхнюю частоту полосы пропускания канала связи. Могут быть и другие соображения относительно выбора значения
можно рассчитать с помощью теоремы Котельникова, выбрав в качестве верхней частоты спектра сшнала, например, верхнюю частоту полосы пропускания канала связи. Могут быть и другие соображения относительно выбора значения  t С учетом дискретизации времени для расчета отсчетов сигналов на ЭВМ
t С учетом дискретизации времени для расчета отсчетов сигналов на ЭВМ  необходимо переписав следующим образом
необходимо переписав следующим образом

где I — номер отсчета сигнала;  — момент времени, для которого рассчитывается отсчет сигнала.
— момент времени, для которого рассчитывается отсчет сигнала.
Число отсчетов сигнала L, приходящихся на единичный интервал времени  легко рассчитать
легко рассчитать  (В — скорость модуляции).
(В — скорость модуляции).
Для уменьшения числа операций, выполняемых в процессе моделирования передатчика, целесообразно заранее рассчитать отсчеты сигналов  а не вычислять их каждый раз по формулам
а не вычислять их каждый раз по формулам  после генерации очередного информационного символа Другими словами, желательно перед программным модулем источника информации сформировать с помощью
после генерации очередного информационного символа Другими словами, желательно перед программным модулем источника информации сформировать с помощью  двумерный массив (матрицу) отсчетов сигначов
двумерный массив (матрицу) отсчетов сигначов 

Таким образом, в первой строке матрицы  будут находиться отсчеты сигнала, соответствующего информационному символу «1», а во второй строке матрицы-—отсчеты сигнала, соответствующего информационному символу
будут находиться отсчеты сигнала, соответствующего информационному символу «1», а во второй строке матрицы-—отсчеты сигнала, соответствующего информационному символу 
Схема алгоритма моделирования частотного модулятора изображена на рис П. 1.5, а программный модуль, написанный на языке Фортран, имсег следующий вид


В этой программе расчет отсчетов на выходе модулятора  осуществляется с помощью оператора цикла DO Напомним, что следующая за DO цифра указывает метку циклически выполняемого оператора (при изменении индекса отсчета
осуществляется с помощью оператора цикла DO Напомним, что следующая за DO цифра указывает метку циклически выполняемого оператора (при изменении индекса отсчета  от 1 до L с шагом, равным 1) В этом и последующих фрагментах программы индексные символы написаны большими буквами, поскольку в Фортране не предусмотрено обозначение индексов малыми подстрочными символами
от 1 до L с шагом, равным 1) В этом и последующих фрагментах программы индексные символы написаны большими буквами, поскольку в Фортране не предусмотрено обозначение индексов малыми подстрочными символами
Моделирование канала связи. При прохождении через канал связи сигнал, во-первых, подвергается искажениям, вызванным неидеальностью элементов аппаратуры и физической среды, но которой он распространяется, а во-вторых, на сигнал воздействуют аддитивные и мультипликативные помехи. Вначале рассмотрим моделирование влияния на сигнал первою фактора — неидеальностн элементов аппаратуры, например, фильтров передающей и приемной сторон аппаратуры, и физической среды, по которой он распространяется.
Свойства канала связи, состоящего из последовательно включенных фильтра передающей стороны, физической среды распространения сигнала, фильтра приемной стороны, можно охарактеризовать импульсной реакцией  являющейся откликом канала на входное воздействие в виде б импульса С учетом дискретного во времени представлений сигналов в ЭВМ канал связи можно описать с помощью модели трансверсального фильтра, имеющего дискретную во времени импульсную реакцию
являющейся откликом канала на входное воздействие в виде б импульса С учетом дискретного во времени представлений сигналов в ЭВМ канал связи можно описать с помощью модели трансверсального фильтра, имеющего дискретную во времени импульсную реакцию  Очевидно, что интервал дискретизации импульсной реакции должен бььь равен интервалу дискретизации сигналов. Исходя из рассматриваемой модели канала связи,
Очевидно, что интервал дискретизации импульсной реакции должен бььь равен интервалу дискретизации сигналов. Исходя из рассматриваемой модели канала связи,  отсчет сигнала на выходе канала связи можно рассчитать по формуле
отсчет сигнала на выходе канала связи можно рассчитать по формуле  представляющей собой дискретный аналог интеграла свертки входного сигнала с импульсной реакцией канала связи (для
представляющей собой дискретный аналог интеграла свертки входного сигнала с импульсной реакцией канала связи (для

На Фортране эту операцию можно записать следующим образом

Для накопления результатов умножения в этом фрагменте программы использован прием, аналогичный рассмотренному в разд. 6 5 при реализации алгоритма работы демодулятора Для расчета отсчетов сигнала  предварительно следует ввести
предварительно следует ввести  начальных отсчетов
начальных отсчетов 
Рассмотренный пример относится к простейшему случаю — моделированию каналов с постоянными параметпамп (с неизменной  ), к которым можно отнести ряд каналов, таких, например, как кабельные каналы, тлинноволновые радиоканалы, световодные каналы. Однако имеется целый ряд каналов гидроакустические, тропосферные и коротковолновые радиоканалы, которые характеризуются изменяющейся с течением времени импульсной реакцией.
), к которым можно отнести ряд каналов, таких, например, как кабельные каналы, тлинноволновые радиоканалы, световодные каналы. Однако имеется целый ряд каналов гидроакустические, тропосферные и коротковолновые радиоканалы, которые характеризуются изменяющейся с течением времени импульсной реакцией.

Рис. П. 1.6. Модель канала связи в виде трапсверсального фильтра (а) и его импульсная реакция (б)
Для их моделпрования необходим дополнительный программный модуль, задачей которого является соответствующее изменение фоомы импульсной реакции
Моделирование источника помех. Для моделирования воздействия на сигнал аддитивных или мультипликативных помех нужно вначале смоделировать источник помех. Помехи, как правило, представляют собой случайные процессы с определенными статическими характеристиками (спектральной плотностью мощности, плотностью распределения вероятностей мгновенных значений, вероятностью распределения интервалов между импульсами для импульсных помех и т. д.)
В каналах связи всегда присутствует помеха типа «белого шума», представляющая собой случайный процесс с равномерной спектральной плотностью мощности и нормальным законом распределения вероятностей мгновенных значений Для ее моделирования удобнее всего воспользоваться имеющейся в математическом обеспечении ЭВМ стандартной подпрограммой CAUSS, генерирующей отсчеты гауссовского случайного процесса с заданными дисперсией (мощностью) D и математическим ожиданием МО. На языке Фортран обращение к этой подпрограмме осуществляется оператором CALL GAUSS (IX, D, МО, R). Здесь IX — служебное число целого типа, содержащее не более девяти цифр и задаваемое в блоке ввода исходных данных После каждого обращения к подпрограмме получается новое случайное число R, имеющее нормальный закон распределения с дисперсией D и математическим ожиданием МО Значения D и МО также должны быть заданы в блоке ввода исходных данных Генерацию и наложение отсчета помехи на отсчет сигнала можно отобразить следующими двумя операторами

Идентификатор SBXPR обозначает отсчет сигнала на входе приемника Моделирование помех с заданным законом распределения вероятностей мгновенных значений. Помимо помех, имеющих нормальный закон распределения вероятностей мгновенных значений, в каналах часто действуют помехи с другими законами распределения.

Рис. П. 1.7. Формирование случайных чисел с необходимой плотностью распределения вероятностей методом кусочной аппроксимации
В качестве исходных случайных процессов для получения процессов с необходимым законом распределения чаще всего используют процессы с равномерным законом распределения вероятностей мгновенных значений в интервале  Как уже упоминалось, программным датчиком случайных чисел с таким законом распределения может служить подпрограмма RANDU. Существуют различные методы преобразования случайных чисел с равномерным законом распределения в случайные числа с заданным законом распределения. Одним из наибопее общих является метод нелинейного преобразования, обратного функции распределения, а также метод кусочной аппроксимации искомой функции распределения Суть этого метода заключается в следующем
Как уже упоминалось, программным датчиком случайных чисел с таким законом распределения может служить подпрограмма RANDU. Существуют различные методы преобразования случайных чисел с равномерным законом распределения в случайные числа с заданным законом распределения. Одним из наибопее общих является метод нелинейного преобразования, обратного функции распределения, а также метод кусочной аппроксимации искомой функции распределения Суть этого метода заключается в следующем
Псть необходимо генерировать случайные числа у с функцией распределения  (рис. П. 1.7, а). Аппроксимируем эту функцию ступенчатой функцией
(рис. П. 1.7, а). Аппроксимируем эту функцию ступенчатой функцией  Обозначим площадь каждой
Обозначим площадь каждой  ступеньки
ступеньки  а границы ее значениями
а границы ее значениями  Разделим диапазон значений равномерно распределенной в интервале
Разделим диапазон значений равномерно распределенной в интервале  случайной величины X, генерируемой подпрограммой RANDU, на подынтервалы, пропорциональные значениям
случайной величины X, генерируемой подпрограммой RANDU, на подынтервалы, пропорциональные значениям  , (рис. П. 1.7, б) Очевидно, что вероятность попадания случайного числа X в
, (рис. П. 1.7, б) Очевидно, что вероятность попадания случайного числа X в  интервал будет равна
интервал будет равна  Тогда алгоритм формирования чисел у с плотностью распределения вероятностей
Тогда алгоритм формирования чисел у с плотностью распределения вероятностей  может быть принят следующим Вначале генерируется число X, Затем определяется, в какой
может быть принят следующим Вначале генерируется число X, Затем определяется, в какой  подынтервал значений X оно попало После этого числу у приписывается значение
подынтервал значений X оно попало После этого числу у приписывается значение  Однако при этом случайные числа у будут принимать лишь дискретный ряд значений
Однако при этом случайные числа у будут принимать лишь дискретный ряд значений  Чтобы получить непрерывный закон распределения
Чтобы получить непрерывный закон распределения  к числу у, можно прибавить равномерно распределенное в интервале
к числу у, можно прибавить равномерно распределенное в интервале  число
число 
Существуют различные модификации этого метода, учитывающие конкретные особенности программного обеспечения ЭВМ.
Моделирование приемника. Задачами приемника являются демодуляция сигнала и, если используется декодер, обнаружение и исправление ошибок Рассмотрим моделирование приемника для простейшего случая, когда его функции сводятся лишь к демодуляции, например, частотно-модулированных сигналов.
Известно большое число методов демодуляции частотно-модулированных сигналов. В качестве примера рассмотрим демодуляцию сигналов с помощью двух фильтров, каждый из которых согласован соответственно с сигналами  Форма сигналов определена с учетом их искажений, вызванные неидеальностью элементов аппаратуры и среды распространения Модули максимумов напряжений на выходах согласованных фильтров при поступлении на а вход приемника сигналов
Форма сигналов определена с учетом их искажений, вызванные неидеальностью элементов аппаратуры и среды распространения Модули максимумов напряжений на выходах согласованных фильтров при поступлении на а вход приемника сигналов  будут равны соответственно
будут равны соответственно

Здесь  обозначают импульсные реакции первого и второго согласованных фильтров,
обозначают импульсные реакции первого и второго согласованных фильтров,  — начало интервала обработки сигнала на выходе канала,
— начало интервала обработки сигнала на выходе канала,  То — конец интервала обработки После вычисления
То — конец интервала обработки После вычисления  производится их сравнение. При этом, если
производится их сравнение. При этом, если  — решение приемника о принятом информационном символе
— решение приемника о принятом информационном символе  в противном случае
в противном случае 
Программный модуль приемника выглядит следующим образом:
 (1)
(1)
Оператор ABS (RE) вычисляет абсолютное значение 
Моделирование счетчика ошибок. Вначале необходимо определить сам факт ошиибки Это можио сделать, сравнивая информационные элементы на выходе источника информации  и на выходе приемника
и на выходе приемника  Если их значения не одинаковы, то в счетчик ошибок следует заслать единицу, свидетельствующую о наличии ошибки Если значения одинаковы, то содержимое счетчика изменять не следует. Реализуются эти операции следующими операторами:
Если их значения не одинаковы, то в счетчик ошибок следует заслать единицу, свидетельствующую о наличии ошибки Если значения одинаковы, то содержимое счетчика изменять не следует. Реализуются эти операции следующими операторами:


Идентификатор OPR обозначает значение ошибки приемника, SUMOPR — сумму ошибок Начальное значение SUMOPR  должно быть задапо и блоке ввода исходных данных
должно быть задапо и блоке ввода исходных данных
После окончания испытания системы оценку вероятности ошибки получают путем деления SUMOPR на количестве проведенных испытании
В заключение определим число основных операций, необходимых для расчета SMAX1 и SMAX2 Для получения L отсчетов сигнала на выходе модулятора потребовалось L операций присваивания значениям SM (I) значений  Далее для расчета с помощью операции свертки L значений сигнала на выходе канала связи необходимо было затратить, не считая операции сдвига, LN сложений и LN умножений (для каждого отсчета N сложений и N умножений).
Далее для расчета с помощью операции свертки L значений сигнала на выходе канала связи необходимо было затратить, не считая операции сдвига, LN сложений и LN умножений (для каждого отсчета N сложений и N умножений).
Наконец, для вычисления SMAX1 и SMAX2 потребовалось  операций сложения и
операций сложения и  операции умножения Таким образом, общее число операций сложения
операции умножения Таким образом, общее число операций сложения  и операций умножения
и операций умножения  При достаточно больших L к N число операций, затрачиваемых только на один цикл испытаний, может быть весьма велико, что скажется на затратах машинного времени, необходимого для проведения исследования модели системы ПДС Поэтому весьма актуальной является проблема создания таких математических моделей систем ПДС, которые сокращали бы число операций, затрачиваемых на каждый цикл испытаний Одну из таких моделей можно создать, описывая математические модели модуляторов, каналов связи и демодуляторов соответствующими матрицами
При достаточно больших L к N число операций, затрачиваемых только на один цикл испытаний, может быть весьма велико, что скажется на затратах машинного времени, необходимого для проведения исследования модели системы ПДС Поэтому весьма актуальной является проблема создания таких математических моделей систем ПДС, которые сокращали бы число операций, затрачиваемых на каждый цикл испытаний Одну из таких моделей можно создать, описывая математические модели модуляторов, каналов связи и демодуляторов соответствующими матрицами  Перемножив эти матрицы, можно получить результирующую матрицу небольшой размерности, отображающую, однако, все существенные свойства модулятора, канала связи и демодулятора Рассмотрим такую матричную модель системы ПДС
Перемножив эти матрицы, можно получить результирующую матрицу небольшой размерности, отображающую, однако, все существенные свойства модулятора, канала связи и демодулятора Рассмотрим такую матричную модель системы ПДС
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
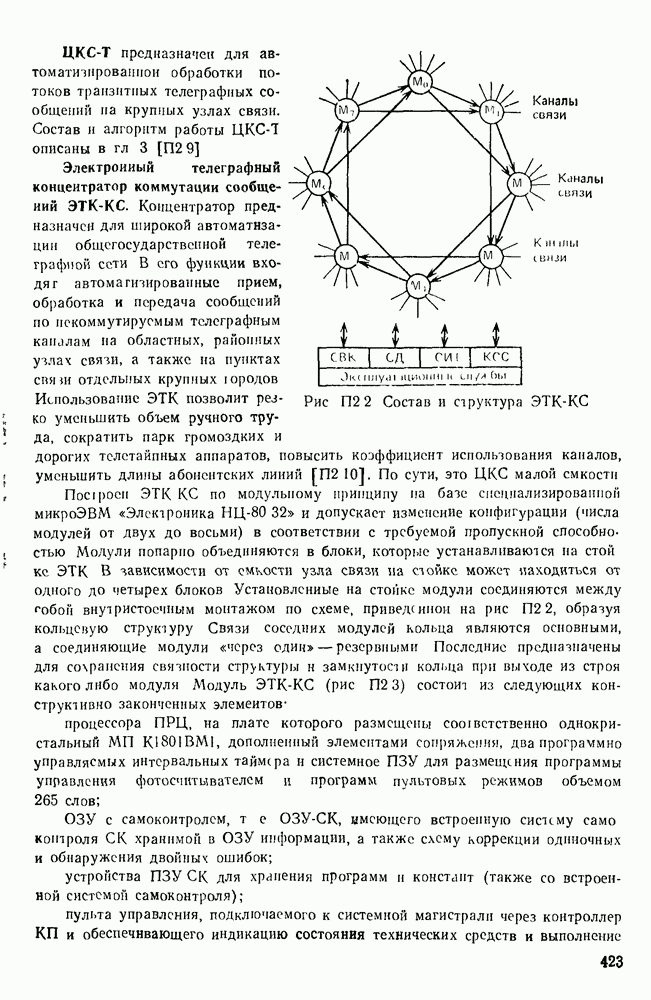
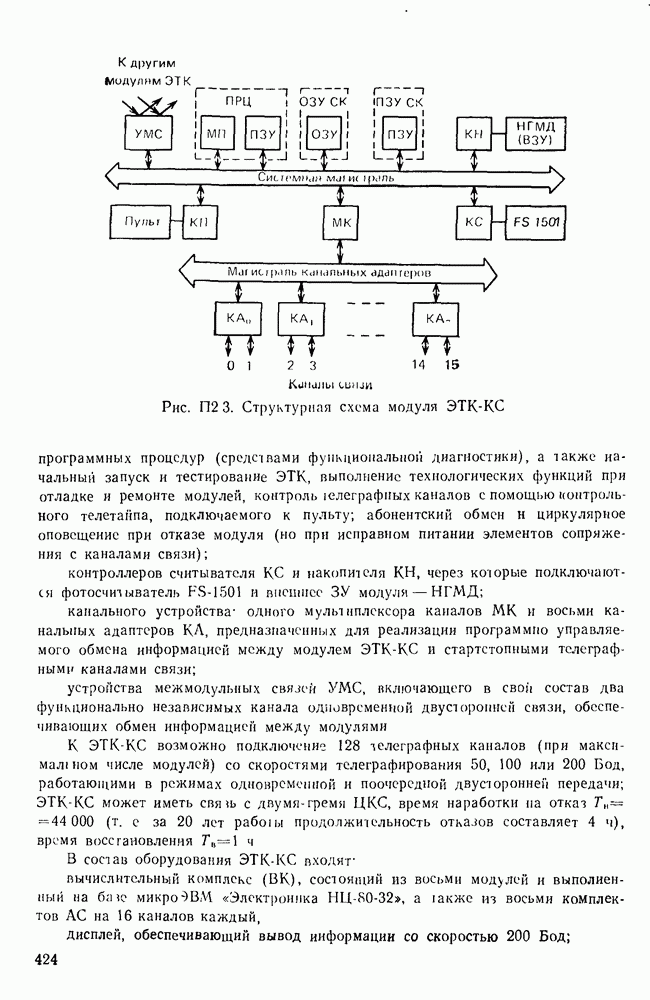
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
- Модулированные сигналы.
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
- Основы микропроцессорной реализации модуляторов УПС.
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
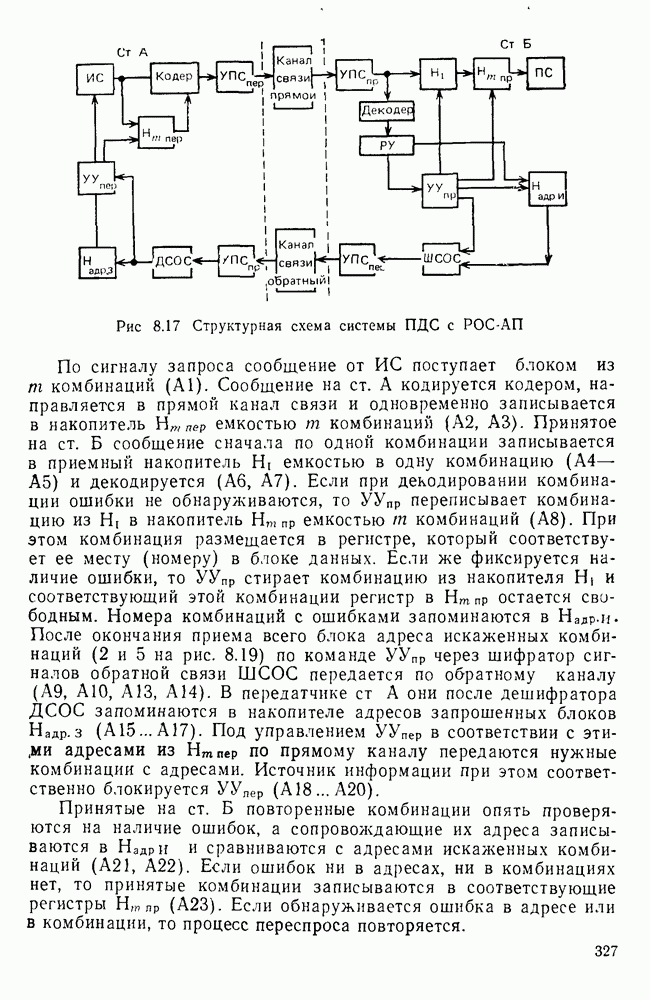
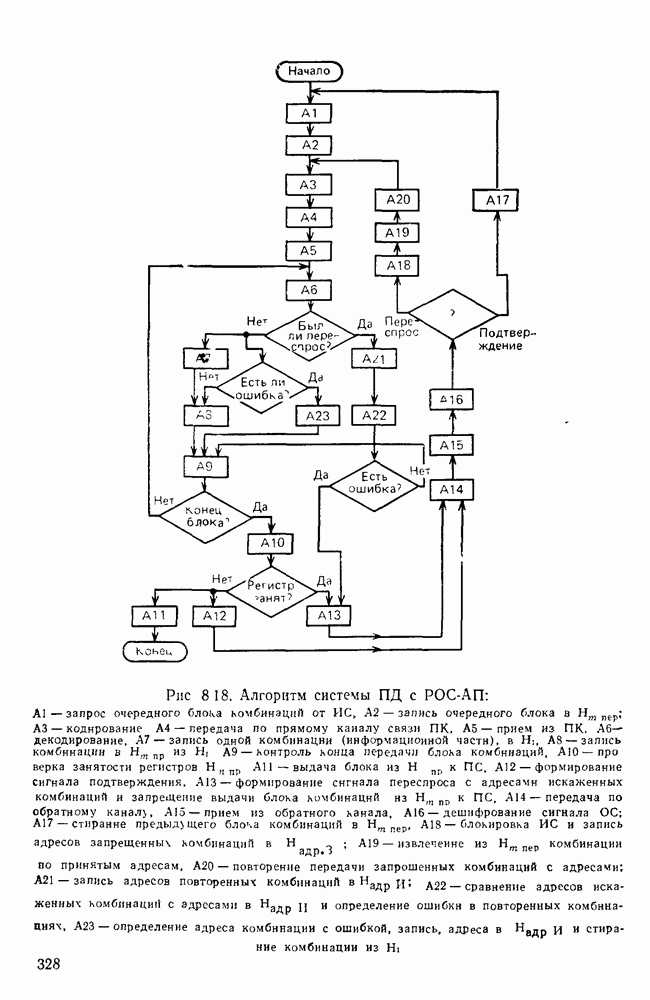
- Система с РОС и адресным переспросом РОС-АП.
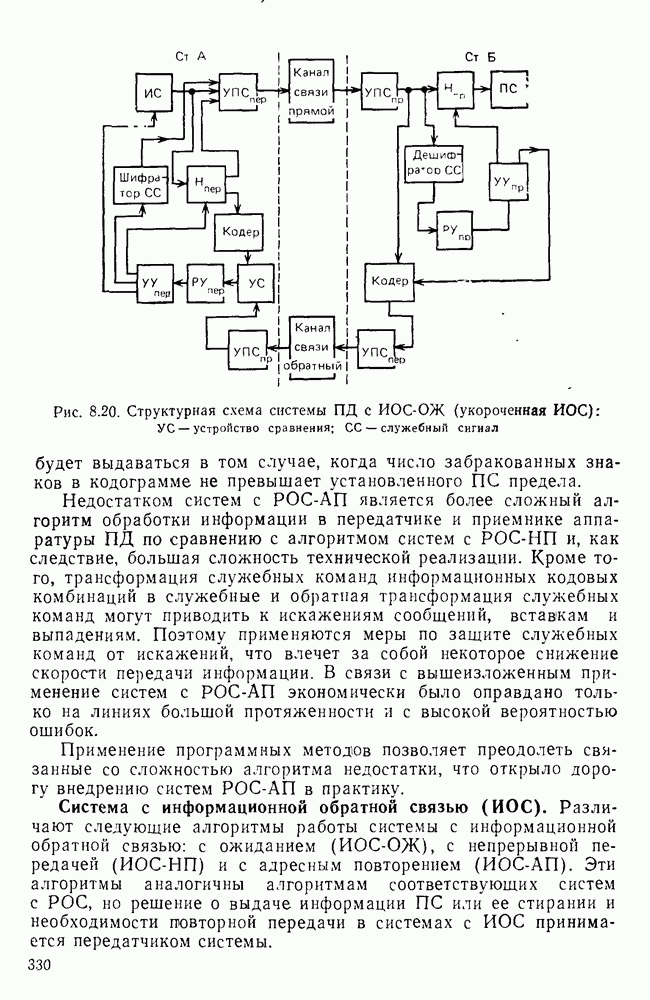
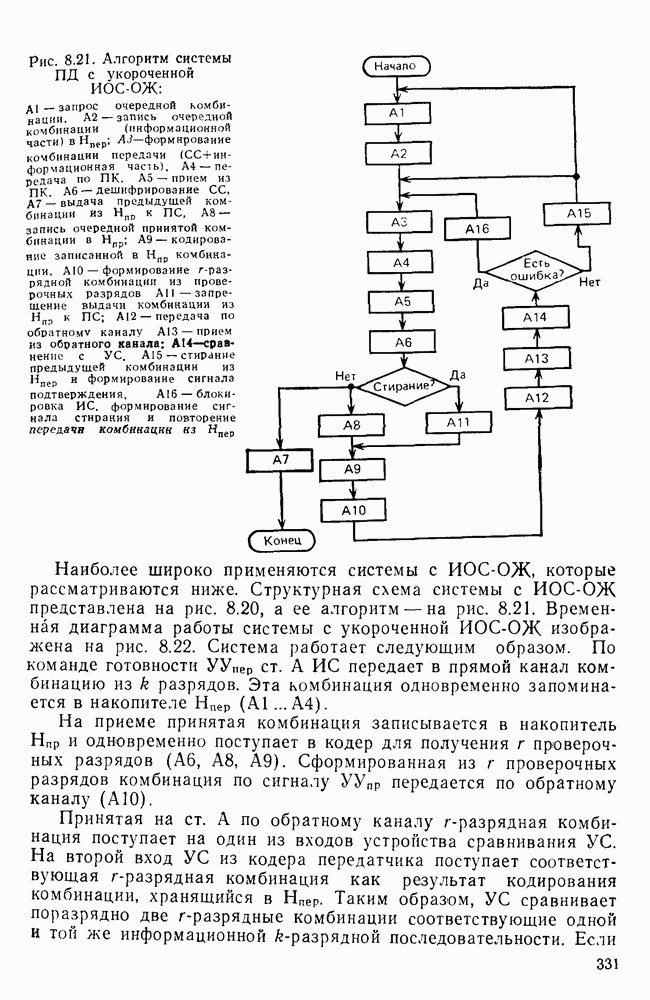
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ