| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Построение кодирующего устройства циклического кода.
В циклических кодах формирование проверочной группы элементов кодовой комбинации происходит делением полинома  на образующий полином
на образующий полином  Так как операция деления в двоичном коде состоит из операций сдвига и сложения по модулю 2, то схемы кодирования содержат упоминавшиеся уже выше типовые элементы двоичной логики. Деление осуществляется схемами, которые называются регистрами с обратными логическими связями, или многотакгными линейными фильтрами. Принцип построения такого устройства рассмотрим на примере кода (9,5) с образующим полиномом
Так как операция деления в двоичном коде состоит из операций сдвига и сложения по модулю 2, то схемы кодирования содержат упоминавшиеся уже выше типовые элементы двоичной логики. Деление осуществляется схемами, которые называются регистрами с обратными логическими связями, или многотакгными линейными фильтрами. Принцип построения такого устройства рассмотрим на примере кода (9,5) с образующим полиномом  Пусть кодируется группа, информационный полином которой имеет вид
Пусть кодируется группа, информационный полином которой имеет вид  Поскольку операция умножения на
Поскольку операция умножения на  означает добавление к соответствующей кодовой комбинации
означает добавление к соответствующей кодовой комбинации  нулей, то никакого специального устройства не требуется, а сдвиг на
нулей, то никакого специального устройства не требуется, а сдвиг на  разряда осуществляется обычным регистром задержки.
разряда осуществляется обычным регистром задержки.

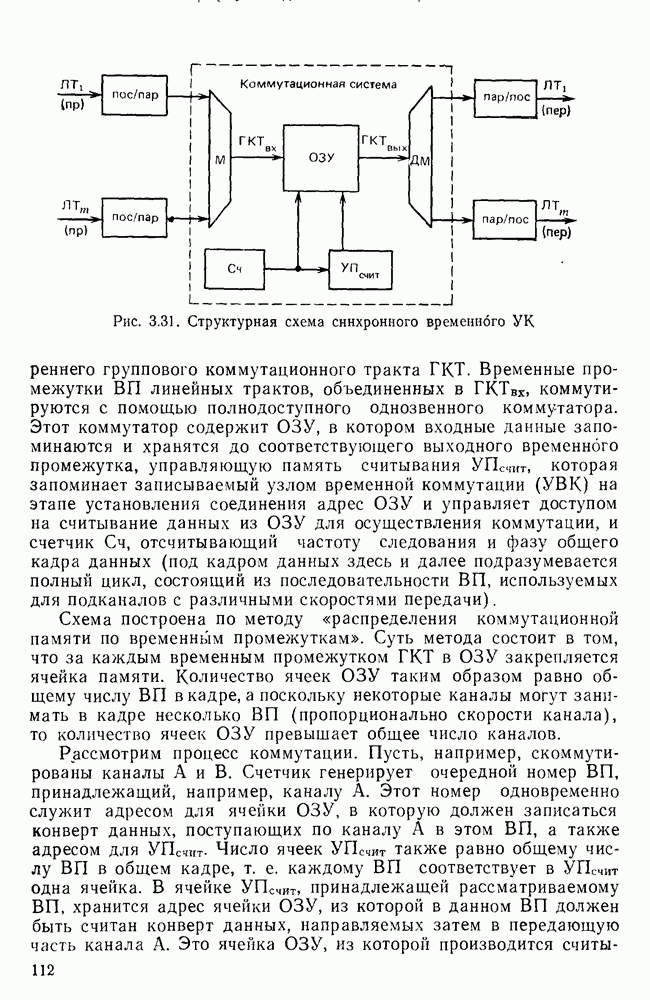
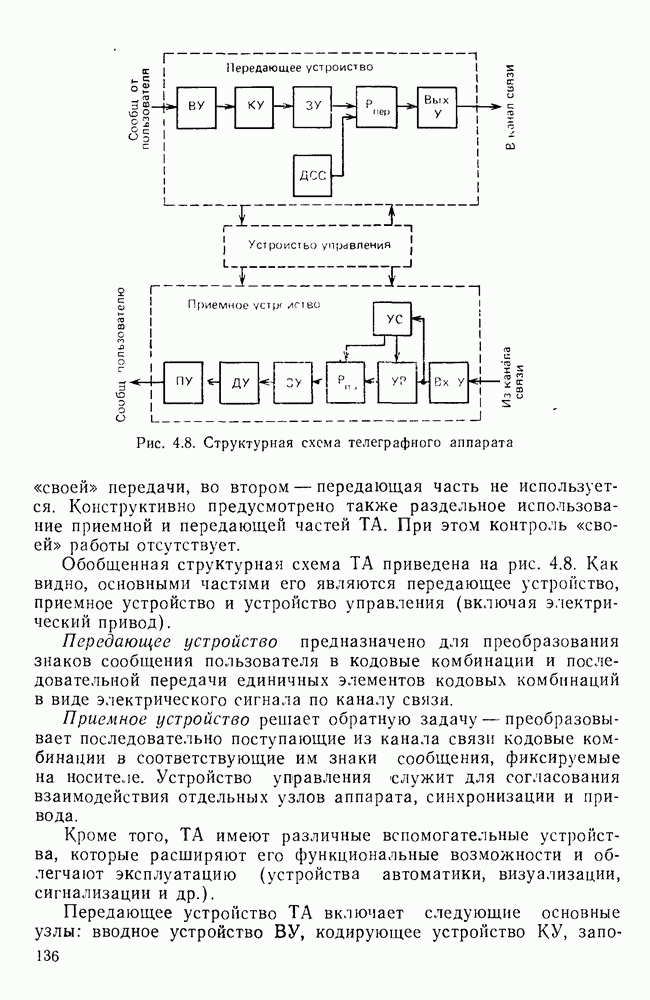
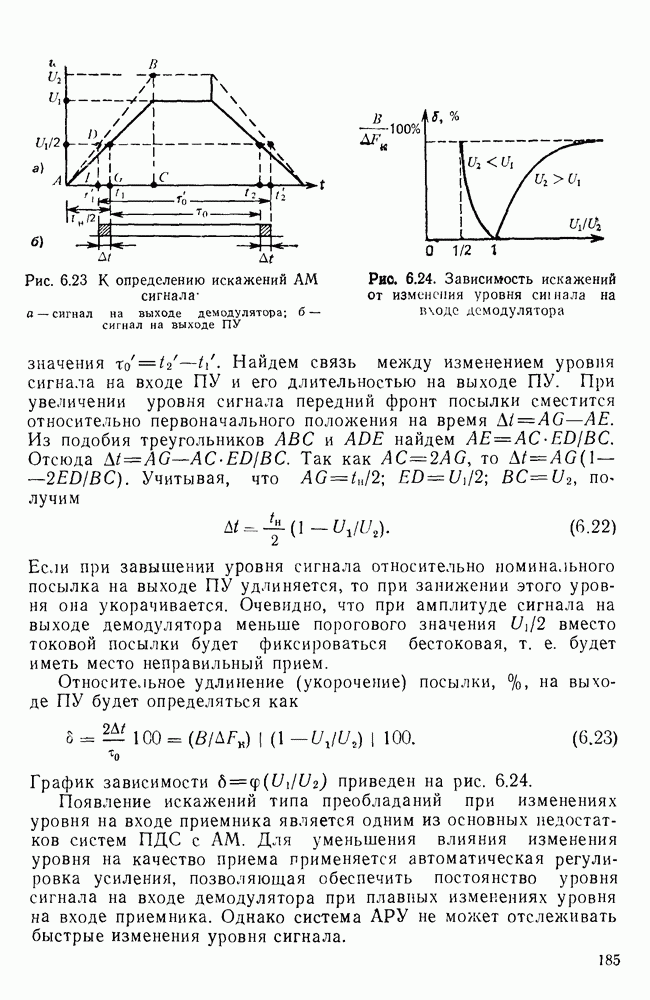
Рис. 7.8. Формирователь остатка циклического кода (9,5)
В данном примере регистр задержки имеет четыре ячейки. Деление производится в многотактном фильтре. Элементы информационной группы подаются на вход первой ячейки регистра, начиная со старшего разряда. Через четыре такта элемент старшего разряда появится на выходе регистра. С пятым тактом выходная ячейка будет свободна от поступления элементов информационной группы и в регистр вводится группа проверочных элементов, представляющая остаток от деления 
Формирователь проверочной группы представляет собой сдвигающий регистр с обратными связями между ячейками. Эти связи реализуются через сумматоры по модулю 2. Указанная схема выполняет деление  на
на  Делимое в виде кодовой группы, представляющей полином
Делимое в виде кодовой группы, представляющей полином  подается на вход сдвигающего регистра, а полином
подается на вход сдвигающего регистра, а полином  вводится в регистр в виде соответствующей подобранной структуры обратных связей через сумматоры. Проверочная группа элементов последовательно формируется на выходе регистра.
вводится в регистр в виде соответствующей подобранной структуры обратных связей через сумматоры. Проверочная группа элементов последовательно формируется на выходе регистра.
Число ячеек сдвигающего регистра выбирается равным степени образующего полинома, а число сумматоров по модулю 2 на единицу меньше его веса (числа членов образующего полинома). В рассматриваемом примере вес полинома  следовательно, должно быть два сумматора. Возможная структура формирователя представлена схемой на рис. 7.8.
следовательно, должно быть два сумматора. Возможная структура формирователя представлена схемой на рис. 7.8.
Предположим, что в некоторый момент  в ячейки регистра при разомкнутом ключе К вводятся четыре разряда информационной группы элементов (старший разряд в выходной ячейке). Таким образом, в исходном положении ячейки будут находиться в состоянии 1101 (соответственно номерам ячеек). С некоторой задержкой
в ячейки регистра при разомкнутом ключе К вводятся четыре разряда информационной группы элементов (старший разряд в выходной ячейке). Таким образом, в исходном положении ячейки будут находиться в состоянии 1101 (соответственно номерам ячеек). С некоторой задержкой  но до прихода очередного тактового импульса ключ К замыкается. В момент прихода тактового импульса единица старшего разряда «выталкивается» на выход и одновременно поступает на сумматор
но до прихода очередного тактового импульса ключ К замыкается. В момент прихода тактового импульса единица старшего разряда «выталкивается» на выход и одновременно поступает на сумматор  где складывается по модулю 2 с «1» младшего разряда. В результате первая ячейка окажется в состоянии
где складывается по модулю 2 с «1» младшего разряда. В результате первая ячейка окажется в состоянии  Одновременно с этим «1», которая определяла состояние первой ячейки в сумматоре
Одновременно с этим «1», которая определяла состояние первой ячейки в сумматоре  складывается с «1» старшего разряда и сумма подается на вторую ячейку. Поэтому вторая ячейка также перейдет в состояние «0». Третья ячейка перейдет в состояние второй, т. е. «1», а четвертая в состояние третьей, т. е. «0».
складывается с «1» старшего разряда и сумма подается на вторую ячейку. Поэтому вторая ячейка также перейдет в состояние «0». Третья ячейка перейдет в состояние второй, т. е. «1», а четвертая в состояние третьей, т. е. «0».

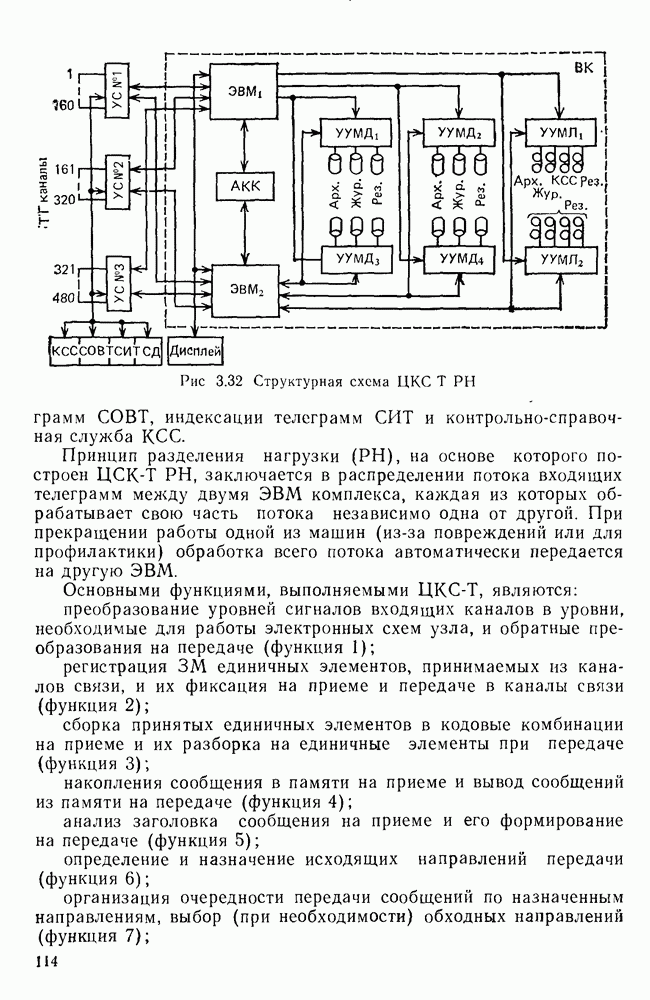
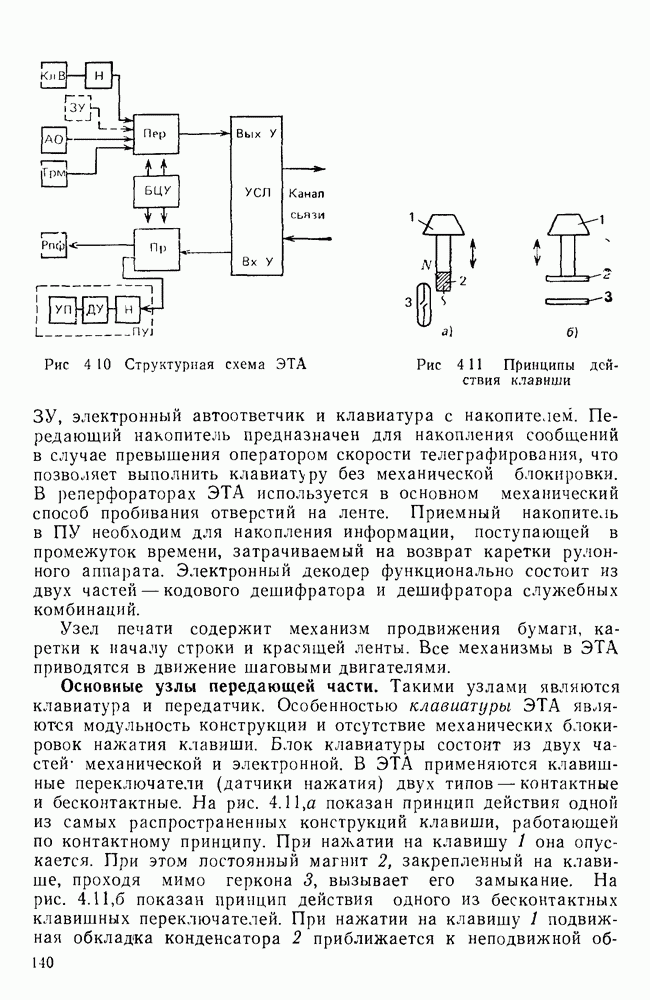
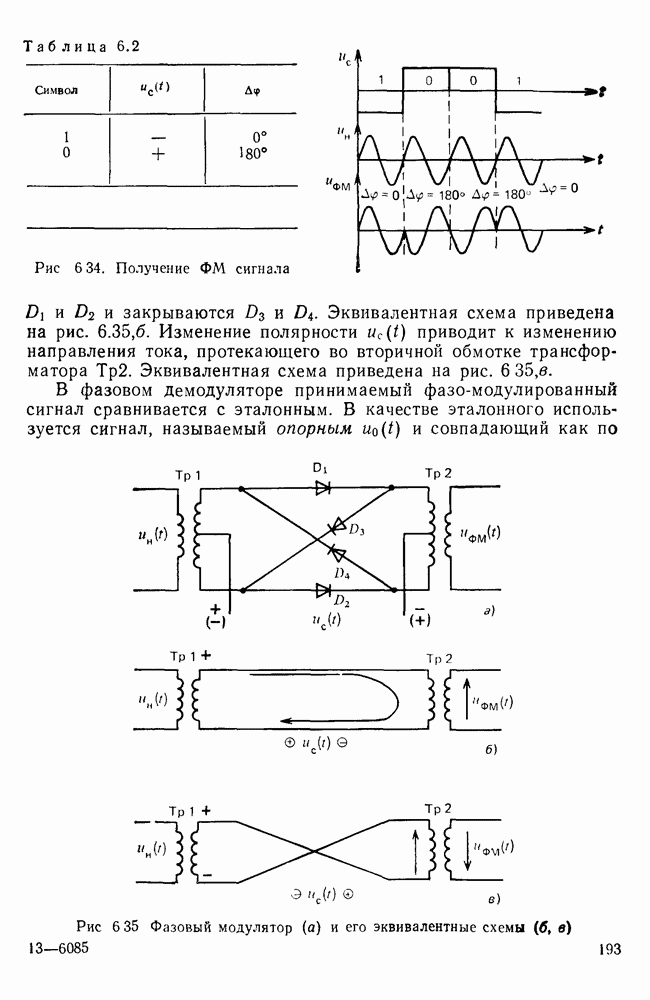
Рис. 7.9. Упрощенная схема кодера циклического кода (9,5)
Таким образом, после первого такта ячейки из состояния 1101 перейдут в состояние 0010, что соответствует двоичному числу 0100. На втором такте на выходе «0» и одновременно появятся «0» на выходах сумматоров  Состояние ячеек после второго такта будет 0001. Третьему — пятому тактам будут соответствовать состояния 1100, ОНО, 0011. Если представить состояния ячеек регистра в виде двоичных чисел (старшим разрядом в четвертой ячейке), то будем иметь: первый такт-0100, второй такт-1000, третий такт ООП, четвертый такт — 0110, пятый такт-1100. Эти числа соответствуют первому, второму и т. д. остаткам от деления числа 101110000 на двоичное число образующего полинома 10011. Проведем это деление:
Состояние ячеек после второго такта будет 0001. Третьему — пятому тактам будут соответствовать состояния 1100, ОНО, 0011. Если представить состояния ячеек регистра в виде двоичных чисел (старшим разрядом в четвертой ячейке), то будем иметь: первый такт-0100, второй такт-1000, третий такт ООП, четвертый такт — 0110, пятый такт-1100. Эти числа соответствуют первому, второму и т. д. остаткам от деления числа 101110000 на двоичное число образующего полинома 10011. Проведем это деление:

Упрощенная структурная схема кодирующего устройства приведена на рис. 7.9. Она содержит: регистр задержки РЗ, обеспечивающий сдвиг информационной группы на четыре такта; формирователь проверочной группы, включающий в себя регистры сдвига и сумматоры по модулю 2 в цепях обратной связи.
В схеме имеются также два ключа  обеспечивающие необходимую последовательность работы схемы. В положении, когда
обеспечивающие необходимую последовательность работы схемы. В положении, когда  замкнут, а
замкнут, а  разомкнут, информационная часть кода подается на вход схемы, т. е. в первую ячейку регистра задержки и через
разомкнут, информационная часть кода подается на вход схемы, т. е. в первую ячейку регистра задержки и через  в первую ячейку регистра сдвига. По окончании четырех тактов старший разряд информационной группы записывается в последние ячейки обоих регистров. Во время пятого такта информационная группа начинает поступать на выход кодера. С этого момента ьлюч
в первую ячейку регистра сдвига. По окончании четырех тактов старший разряд информационной группы записывается в последние ячейки обоих регистров. Во время пятого такта информационная группа начинает поступать на выход кодера. С этого момента ьлюч  размыкается, а ключ
размыкается, а ключ  замыкается. Начиная с пятого такта, формирователь проверочной группы работает в соответствии с ранее описанной процедурой. После девятого такта ключ
замыкается. Начиная с пятого такта, формирователь проверочной группы работает в соответствии с ранее описанной процедурой. После девятого такта ключ  размыкается, а
размыкается, а  замыкается. С этого момента формирователь проверечной группы работает как обычный регистр сдвига, «выталкивая» на вход кодера записанные в ячейках регистра проверочные разряды. Одновременно в регистры начинают поступать новые информационные разряды.
замыкается. С этого момента формирователь проверечной группы работает как обычный регистр сдвига, «выталкивая» на вход кодера записанные в ячейках регистра проверочные разряды. Одновременно в регистры начинают поступать новые информационные разряды.
Структура декодера с обнаружением ошибок аналогична кодирующему устройству. Она содержит в качестве основного блока схему деления. В случае исправления ошибок схема декодера значительно усложняется, поскольку содержит в своем составе определитель места ошибки.
Сложность устройств кодирования и декодирования циклического кода.
В соответствии со структурой кодирующего устройства его сложность должна быть пропорциональна длине кодовой комбинации п. В [7.1] показано, что сложность построения кодера циклического кода не превосходит величины  Таким образом, сложность кодирующих устройств циклических кодов растет пропорционально
Таким образом, сложность кодирующих устройств циклических кодов растет пропорционально  , а не
, а не  как это было для линейных нециклических кодов. При исправлении ошибок методом синдромного декодирования так же, как и для нециклических кодов, сложность декодирующих устройств циклических кодов носит экспоненциальный характер. Для кодов БЧХ, исправляющих пакеты ошибок, были разработаны специальные методы декодирования, позволяющие упростить их техническую реализацию. Не вдаваясь в сущность этих способов [7.1], отметим, что сложность построения декодирующих устройств с исправлением ошибок
как это было для линейных нециклических кодов. При исправлении ошибок методом синдромного декодирования так же, как и для нециклических кодов, сложность декодирующих устройств циклических кодов носит экспоненциальный характер. Для кодов БЧХ, исправляющих пакеты ошибок, были разработаны специальные методы декодирования, позволяющие упростить их техническую реализацию. Не вдаваясь в сущность этих способов [7.1], отметим, что сложность построения декодирующих устройств с исправлением ошибок 
т. е. растет почти по линейному закону.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
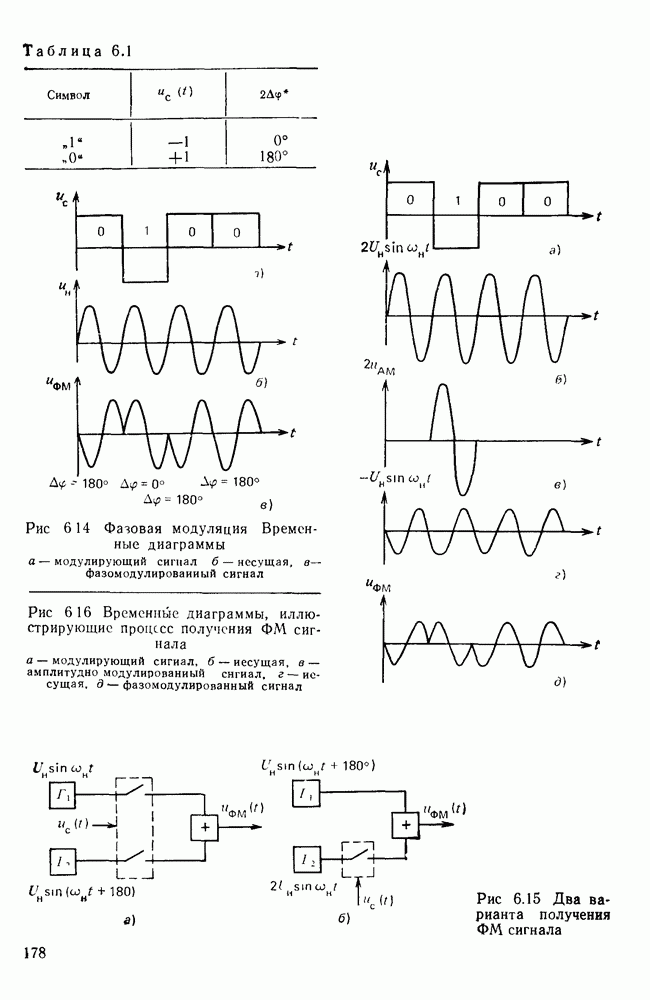
- Модулированные сигналы.
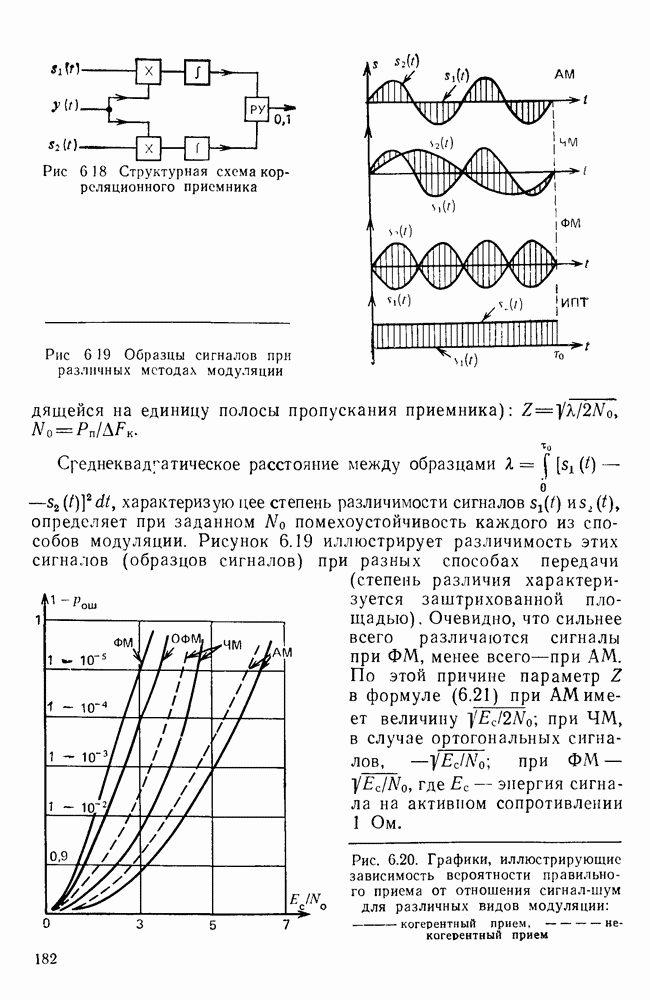
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
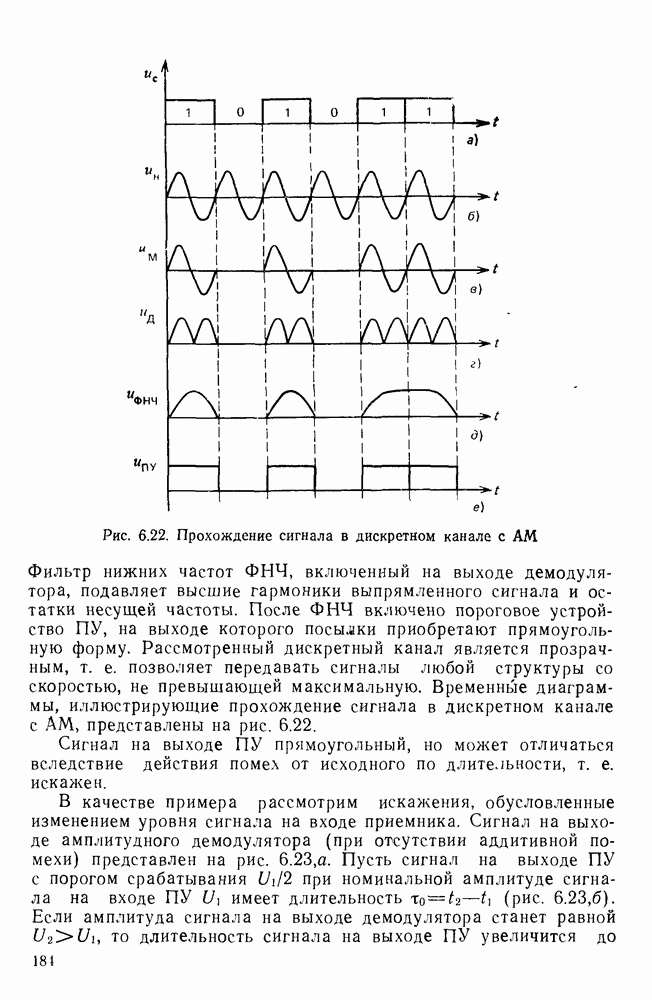
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
- Основы микропроцессорной реализации модуляторов УПС.
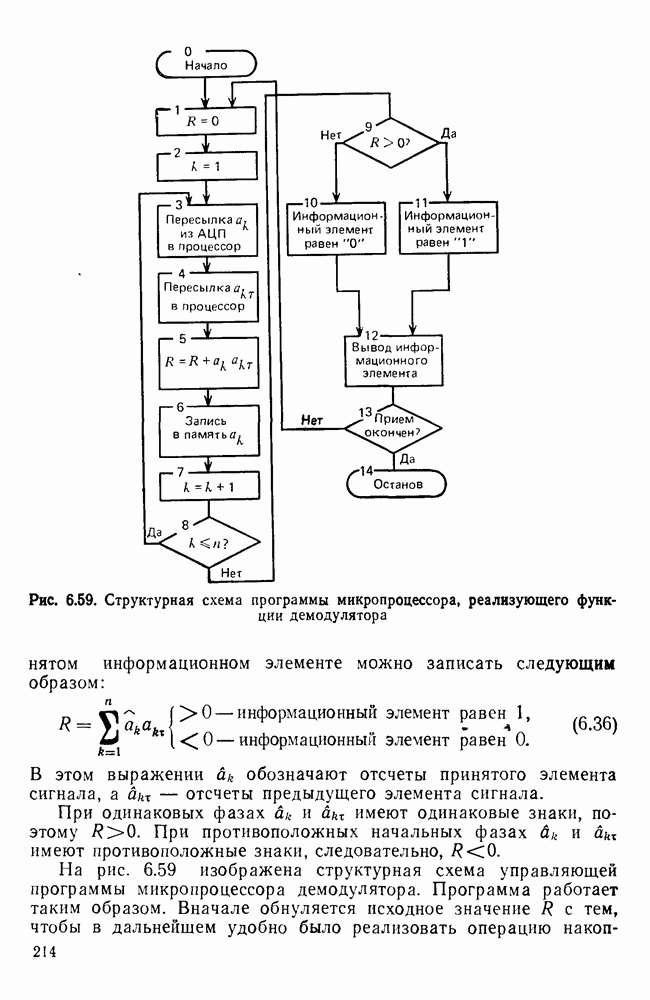
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
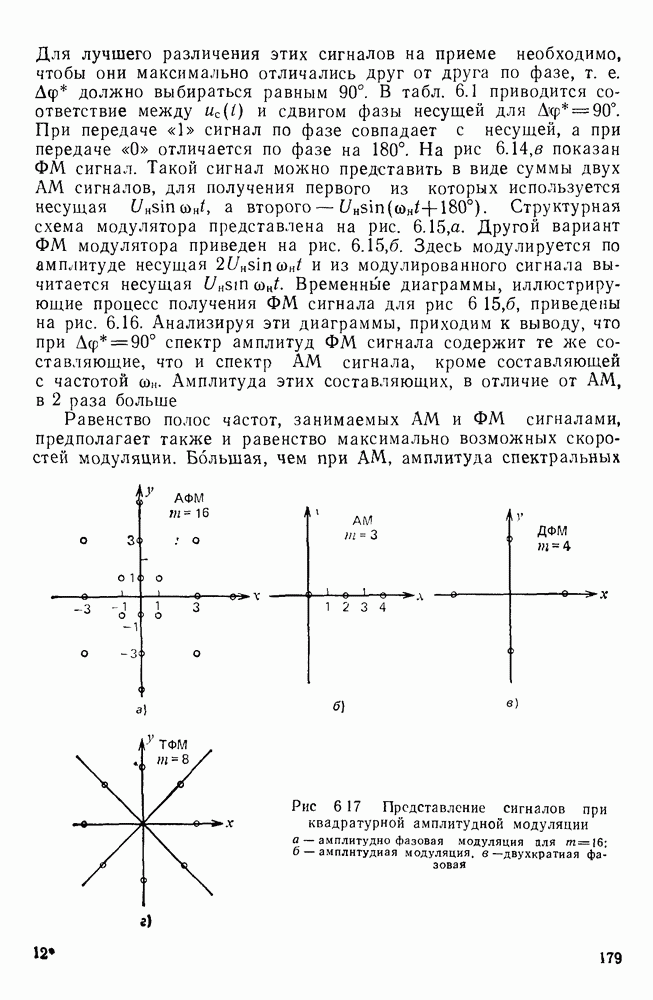
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
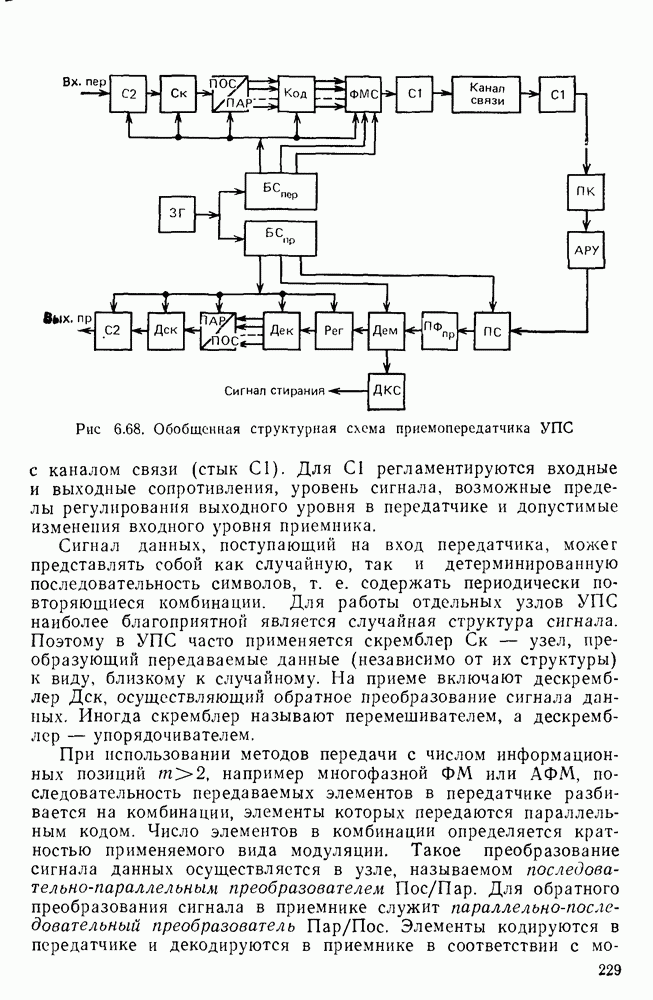
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
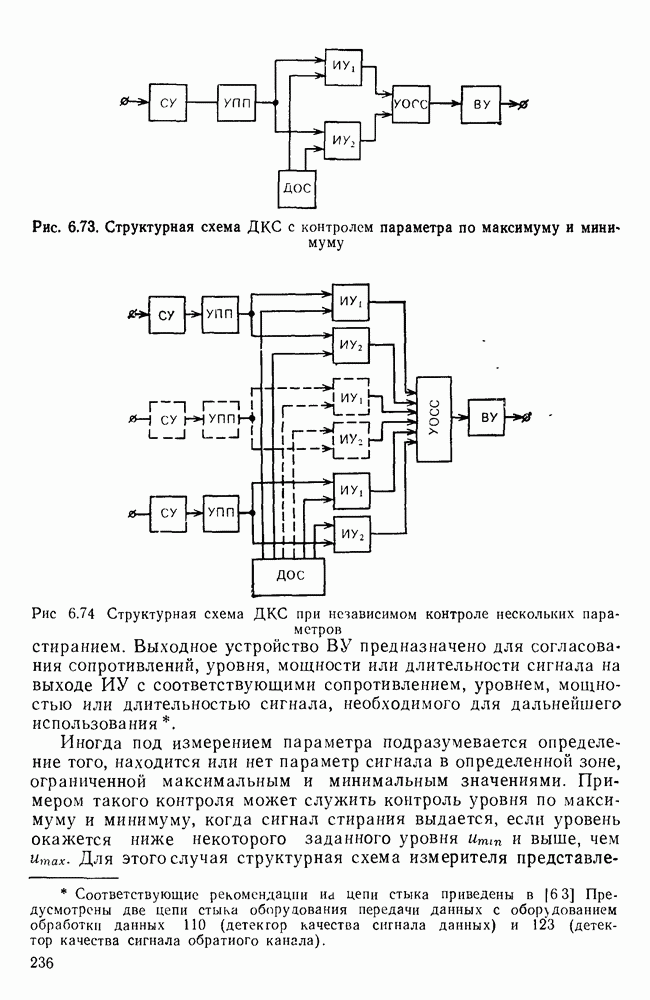
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
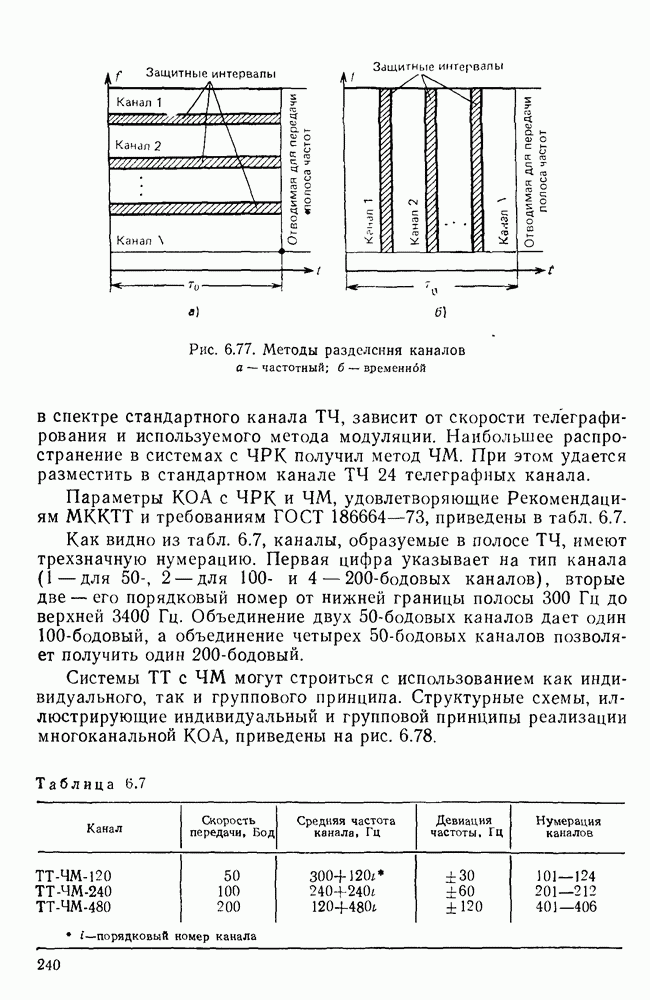
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
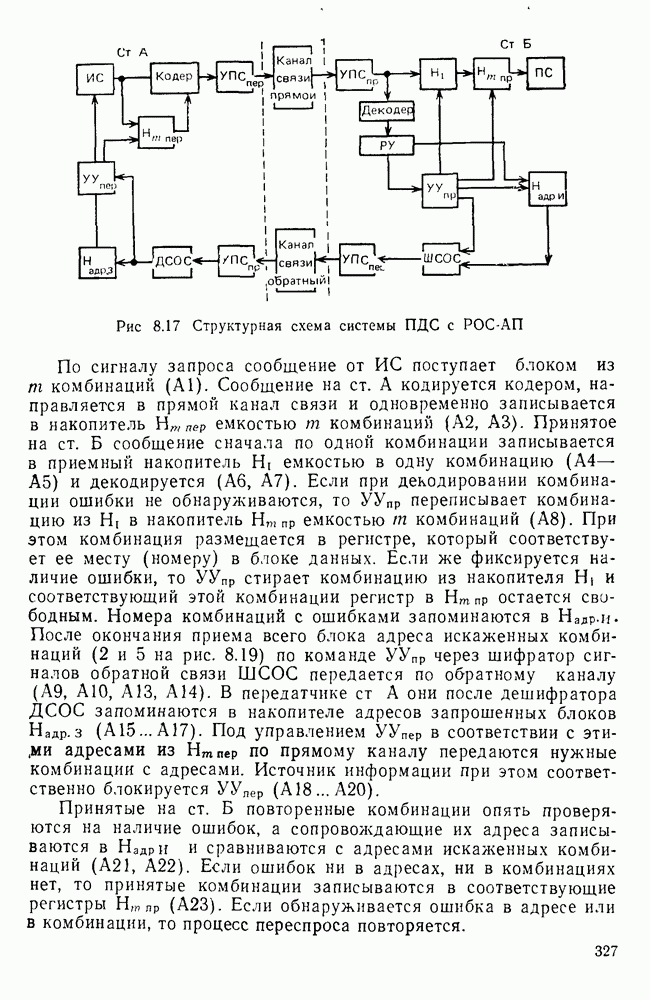
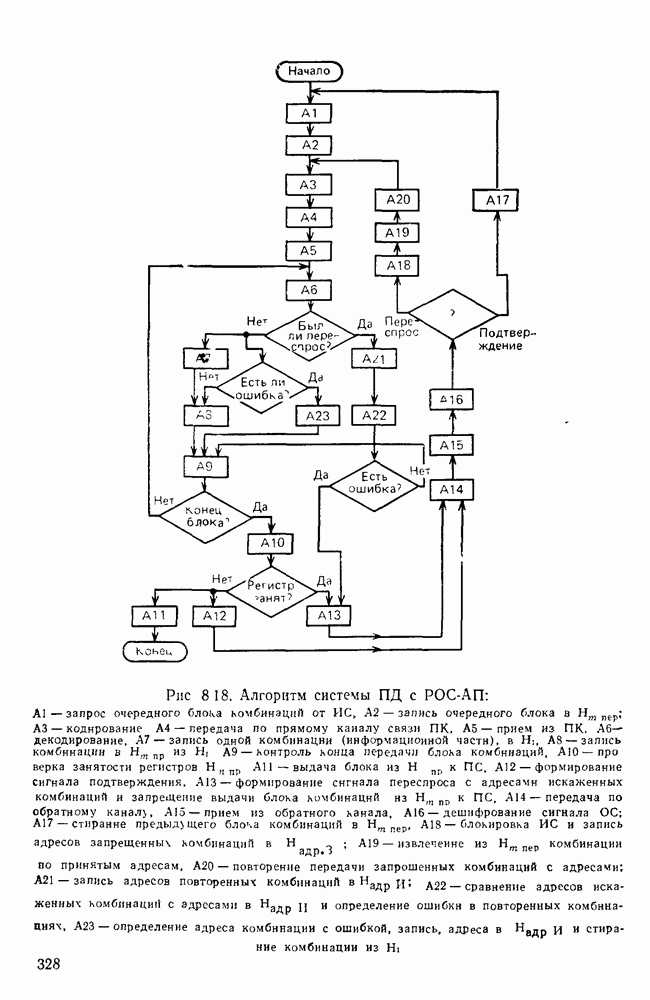
- Система с РОС и адресным переспросом РОС-АП.
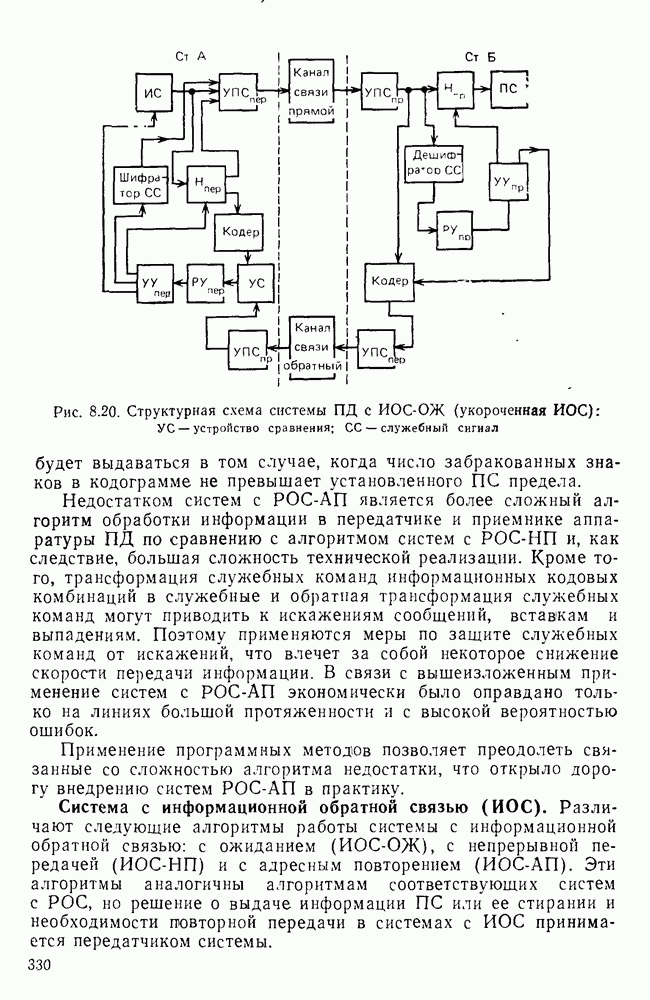
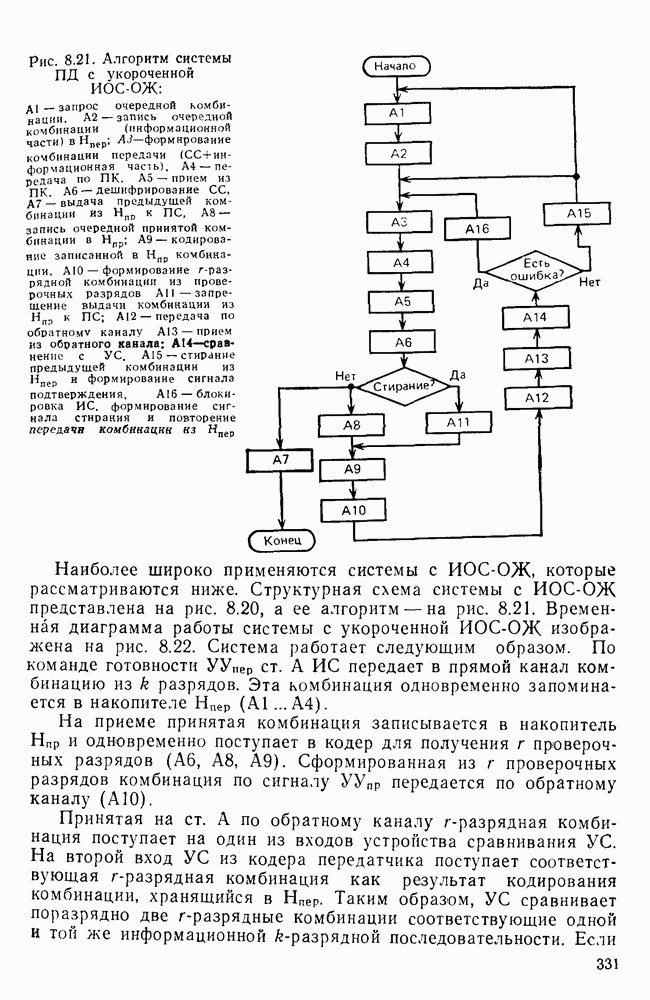
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
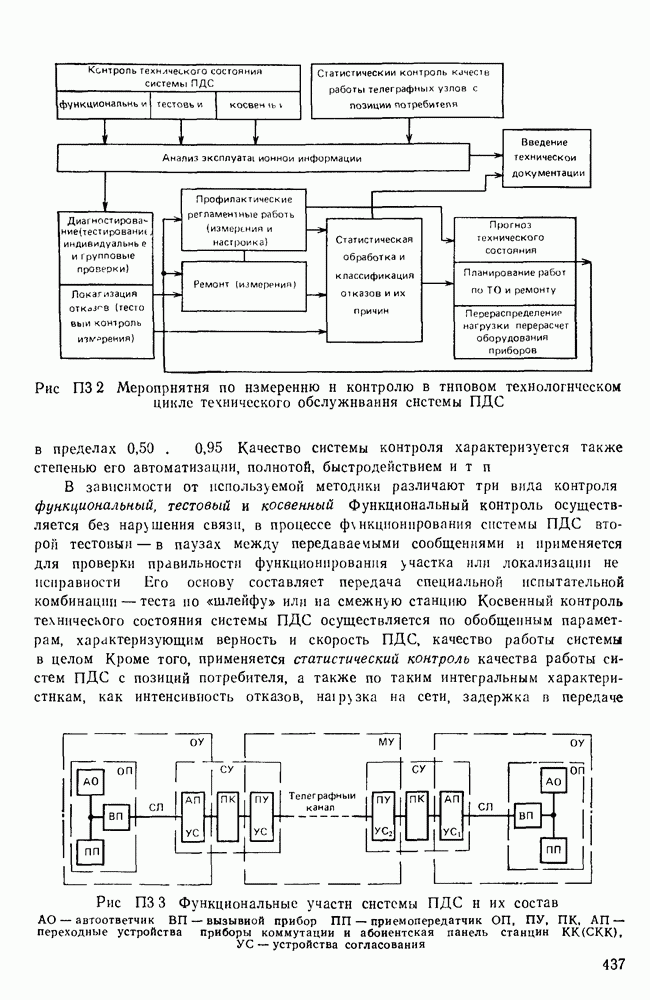
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ