| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
П. 1.1. ОСНОВНЫЕ ПОНЯТИЯ
При решении задач разработки, создания и эксплуатации систем ПДС часто возникают ситуации, когда аналитическое решение задачи оценки помехоустойчивости ввиду значительных математических трудностей невозможно В этих случаях, как правило, используют имитационное математическое моделирование исследуемой системы ПДС на ЭВМ Под имитационным моделированием системы обычно понимается воспроизведение происходящих в ней процессов с искусственной имитацией случайных величин, от которых зависят эти процессы Основой имитационного моделирования является имитационная математическая модель (ИММ) исследуемой системы
Имитационная математическая модель представляет собой алгоритм выполнения вычислительной машинной последовательности действий, представляющих собой имитацию элементарных явлений, составляющих исследуемый процесс, с сохранением их логической структуры и последовательности протекания во времени Другими словами, ИММ представляет собой оформленный в виде программы для ЭВМ алгоритм функционирования исследуемого объекта Реализация этой программы на ЭВМ позволяет находить искомый показатель эффективности исследуемого объекта при заданных значениях его параметров Широкое применение получил метод имитационного моделирования систем связи, базирующийся на описании случайных процессов (сигналов и помех) с помощью систем стохастических дифференциальных уравнений Такой способ имитационного моделирования систем связи позволяет успешно решать как задачи синтеза оптимальных устройств связи, так и задачи их анализа при воздействии случайных помех
Чаще всего ИММ реализуется на основе так называемого функционального метода При этом математическая имитационная модель, системы связи, представляется в виде совокупности операторов или процедур (программных модулей), соответствующих отдельным функциональным элементам (источнику информации, модулятору, каналу связи и так далее) моделируемой системы Состав модулей в общем случае зависит от назначения и характера объекта и целей исследования Функциональный метод позволяет легко отображать существенные взаимосвязи элементов моделируемого объекта, а также воздействие различных внешних факторов, имеющих как детерминированный, так и вероятностный характер
В отличие от других методов имитационное моделирование оказывается весьма удобным аппаратом для исследования широкого круга сложных систем, к которым относятся, в частности, системы и сети связи, и позволяет получать результаты даже тогда, когда применение аналитических методов расчета невозможно в силу математических трудностей
Так, имитационное моделирование оказывается весьма удобным аппаратом для исследования случайных процессов, особенно характерных для функционирования систем и сетей связи Например, при использовании аналитических методов для исследования процессов передачи информации с учетом случайных факторов обычно возникают значительные трудное! и, связанные с тем, что зависимости между случайными факторами (например, помехами) и показателями качества функционирования (например, вероятностью ошибки) описываются сложными математическими выражениями, а иногда даже невозможно установить эти взаимосвязи Для метода имитационного моделирования указанные трудности обычно сравнительно легко преодолимы
При моделировании процессов передачи информации с учетом действия случайных факторов необходимо иметь в виду следующие обстоятельства. Результаты моделирования одной реализации процесса передачи информации в силу действия случайных факторов будут сами по себе реализацией случайного процесса и не могут достаточно полно характеризовать изучаемую систему или сеть связи Поэтому искомые характеристики системы или сети связи при исследовании их методом имитационного моделирования обычно определяют как средние значения по данным большого числа реализаций процесса передачи информации В силу закона больших чисел при большом числе реализаций средние значения определяемых величин приобретают статистическую устойчивость и с достаточной для практики точностью могут быть приняты в качестве приближенных значений искомых величин
Метод имитационного моделирования можно считать распространением на сложные системы применявшегося ранее только в специфических случаях одною из численных методов — метода статистических испытаний или метода Монте-Карло
Основные требования, предъявляемые к ИММ. Главные требования, которым должна удовлетворять разрабатываемая ИММ — это, с одной стороны, простота, а с другой стороны, достаточная точность отображения тех свойств реального объекта, которые подлежат исследованию Эти требования противоречивы, так как желание повысить точность воспроизведения исследуемых характеристик приводит к усложнению модели В результате модель может оказаться настолько сложной и громоздкой, что в итоге для получения одной реализации процесса потребуется значительное машинное время Возрастание сложности модели, а следовательно, и времени испытания увеличивает вероятность сбоев, так что чрезмерно сложные модели могут оказаться неработоспособными Поэтому при разработке модели необходимо на основе имеющейся априорной информации о структуре и назначении моделируемого объекта, задачах и точности испытаний руководствоваться принципом создания модели предельной простоты Этою можно достичь правильным подходом к отбору наиболее существенных факторов и рациональным выбором структуры модели
Последовательность операций при разработке модели и ошибки моделирования. На первом лапе осуществляется формулировка задачи исследования Далее следует содержательное описание процесса функционирования исследуемого объекта После этого приступают к разработке структурной схемы (алгоритма) модели Затем производят уточнение и отбор наиболее существенных факторов, влияющих на исследуемые характеристики объекта моделирования С у четом проведенного отбора производят возможное упрощение модели, после чего приступают к разработке алгоритма модели и программы его реализации на ЭВМ
Программу моделирования объекта исследования опробуют и при необходимости вносят коррективы в разработанную программу. Наконец, производят исследования искомых характеристик модели, анализируют результаты исследований и оценивают их точность При оценке точности полученных результатов исследования важно знать причины, снижающие точность расчета Основные из них следующие ошибки моделирования, возникающие при упрощении моделирующего алгоритма (любая математическая модель — лишь упрощенное представление моделируемою объекта), ошибки моделирования, возникающие из-за необходимой для реализации на ЭВМ дискретизации во времени моделируемых процессов, ошибки моделирования, являющиеся результатом неточного знания, а следовательно,  задания в модели исходных данных (например, мощности помех, законов распределения вероятностен их мгновенных значений, спектральных плотностей и т. п. ), случайные ошибки моделирования, обусловленные ограниченностью количества реализаций случайных процессов (числа испытаний).
задания в модели исходных данных (например, мощности помех, законов распределения вероятностен их мгновенных значений, спектральных плотностей и т. п. ), случайные ошибки моделирования, обусловленные ограниченностью количества реализаций случайных процессов (числа испытаний).
Среди перечисленных причин ошибок существенное значение имеет ограниченность числа испытаний  Влияние
Влияние  на точность результатов моделирования будет рассмотрено далее.
на точность результатов моделирования будет рассмотрено далее.
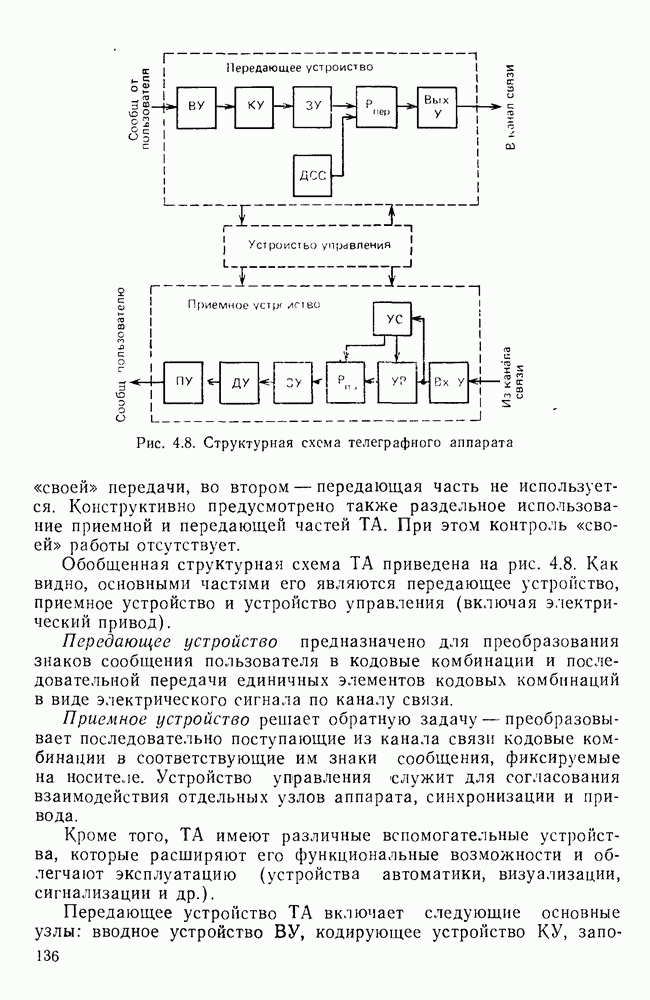
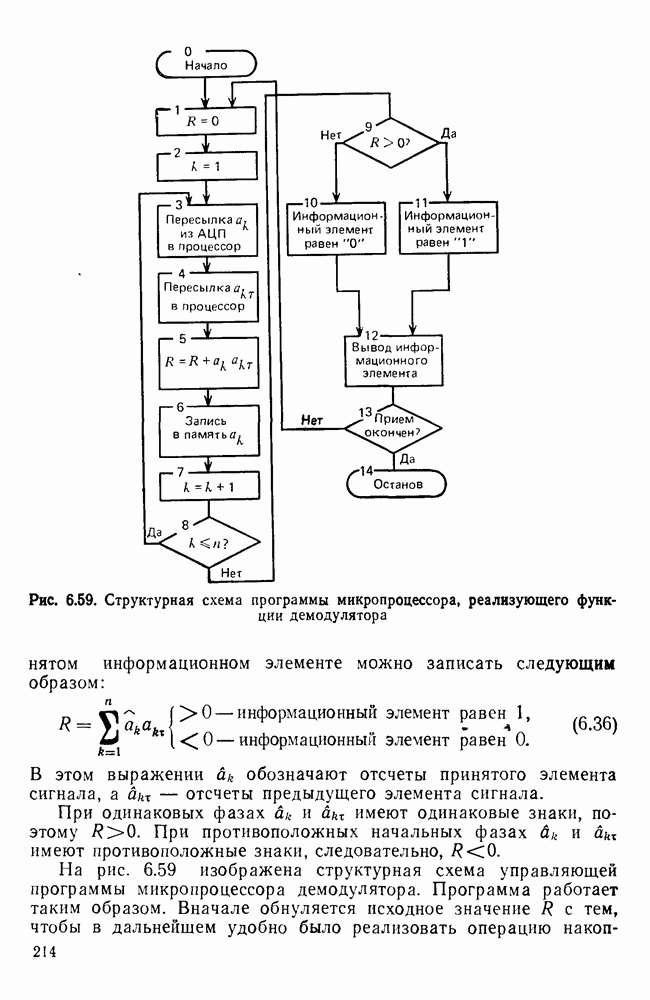
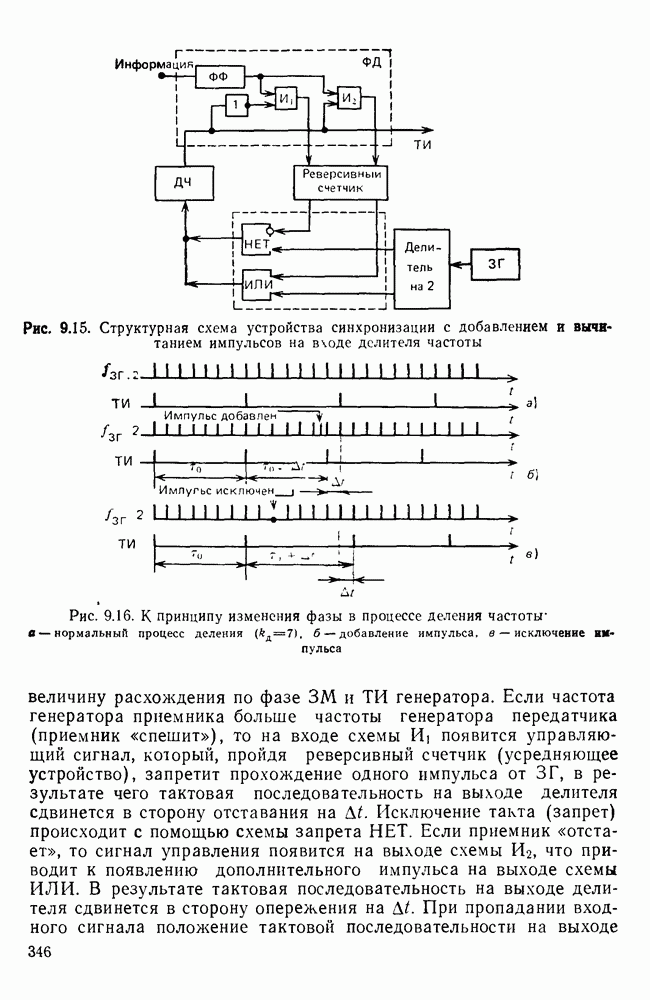
На рис П. 1.1. изображена упрощенная структурная схема исследуемой системы ПДС Она содержит двоичный источник сообщений ИС, вырабатывающий случайным образом образом информационные символы  или «I». Эти символы поступают в передатчик Пер. Передатчик может содержать кодер и модуля
или «I». Эти символы поступают в передатчик Пер. Передатчик может содержать кодер и модуля  На выходе модулятора получается модулированный сигнал, который поступает в канал связи. В канале связи сигнал искажается вследствие неидеальности частотных характеристик канала, а также наложения помех, имеющих случайную природу Таким образом, на входе приемника Пр сигнал носит вероятностный характер, обусловленный случайным характером информационных символов и помех Приемник осуществляет фильтрацию сигнала от помех, его демодуляцию и декодирование Из-за искажений сигнала приемник не всегда может правильно определить, какой из символов
На выходе модулятора получается модулированный сигнал, который поступает в канал связи. В канале связи сигнал искажается вследствие неидеальности частотных характеристик канала, а также наложения помех, имеющих случайную природу Таким образом, на входе приемника Пр сигнал носит вероятностный характер, обусловленный случайным характером информационных символов и помех Приемник осуществляет фильтрацию сигнала от помех, его демодуляцию и декодирование Из-за искажений сигнала приемник не всегда может правильно определить, какой из символов  или «I» передавался Важнейшим пока зателем эффективности системы передачи дискретных сообщений является вероятность ошибки
или «I» передавался Важнейшим пока зателем эффективности системы передачи дискретных сообщений является вероятность ошибки  на выходе приемника Как уже отмечалось, из-за сложноности процессов, происходящих в системе ПДС, не всегда удается получить аналитическое выражение для расчета
на выходе приемника Как уже отмечалось, из-за сложноности процессов, происходящих в системе ПДС, не всегда удается получить аналитическое выражение для расчета 

Рис. П. 1.1. Упрощенная структурная схема исследуемой системы ПДС

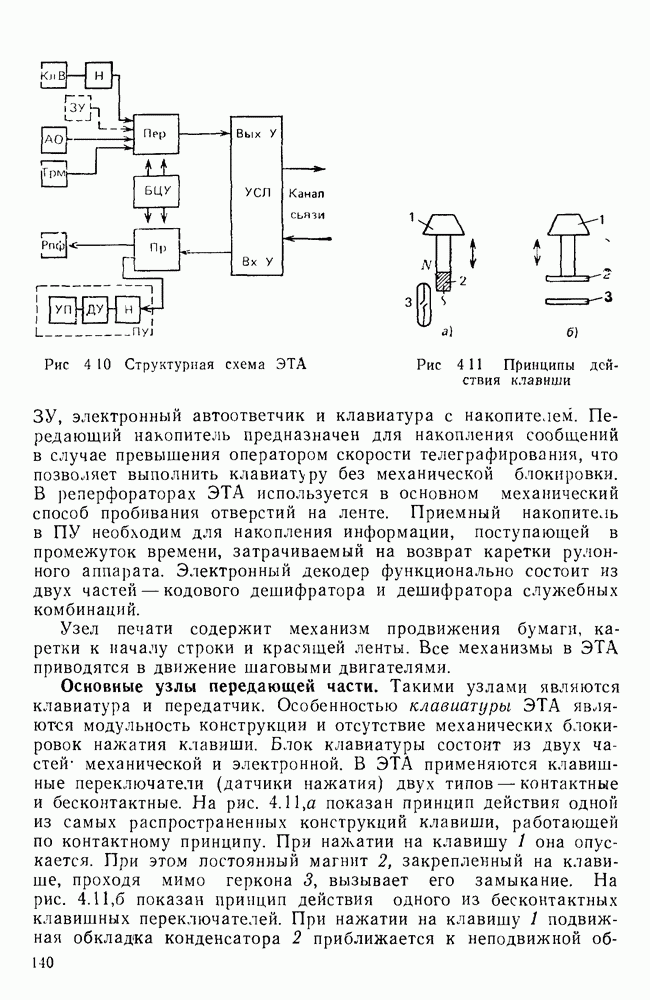
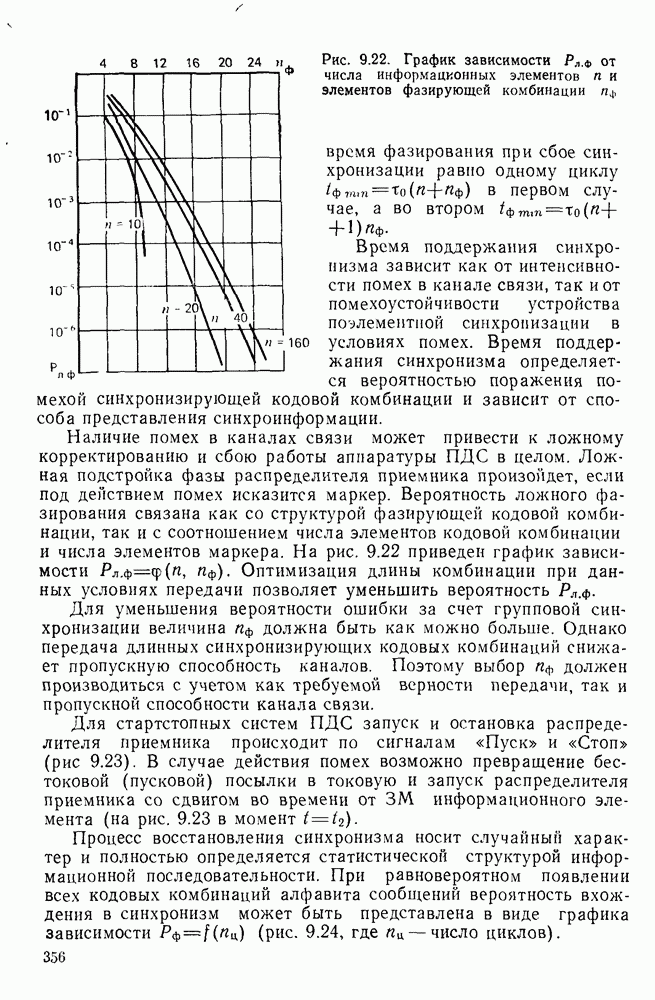
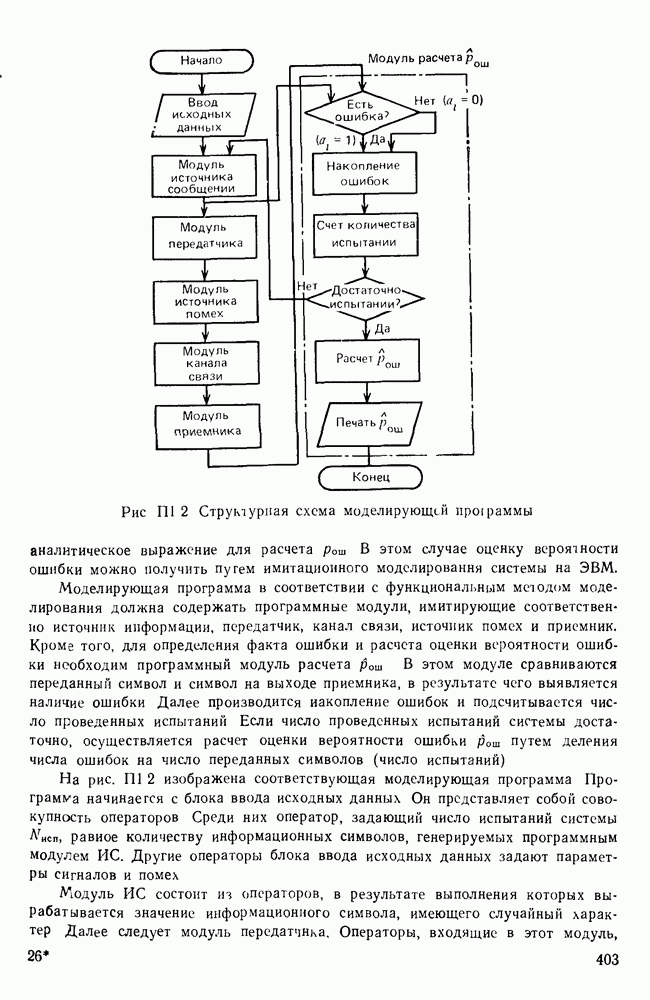
Рис. П. 1.2 Структурная схсма моделирующей прсмраммы
В этом случае оценку вероятности ошибки можно получить пугем имитационного моделирования системы на ЭВМ.
Моделирующая программа в соответствии с функциональным методом моделирования должна содержать программные модули, имитирующие соответственно источник информации, передатчик, канал связи, источник помех и приемник. Кроме того, для определения факта ошибки и расчета оценки вероятности ошибки необходим программный модуль расчета  В этом модуле сравниваются переданный символ и символ на выходе приемника, в результате чего выявляется наличие ошибки Далее производится накопление ошибок и подсчитывается число проведенных испытаний Если число проведенных испытаний системы достаточно, осуществляется расчет оценки вероятности ошибки
В этом модуле сравниваются переданный символ и символ на выходе приемника, в результате чего выявляется наличие ошибки Далее производится накопление ошибок и подсчитывается число проведенных испытаний Если число проведенных испытаний системы достаточно, осуществляется расчет оценки вероятности ошибки  путем деления числа ошибок на число переданных символов (число испытаний)
путем деления числа ошибок на число переданных символов (число испытаний)
На рис.  изображена соответствующая моделирующая программа Программа начинается с блока ввода исходных данных Он представляет собой совокупность операторов Среди них оператор, задающий число испытаний системы Лгисп, равное количеству информационных символов, генерируемых программным модулем ИС. Другие операторы блока ввода исходных данных задают параметры сигналов и помех
изображена соответствующая моделирующая программа Программа начинается с блока ввода исходных данных Он представляет собой совокупность операторов Среди них оператор, задающий число испытаний системы Лгисп, равное количеству информационных символов, генерируемых программным модулем ИС. Другие операторы блока ввода исходных данных задают параметры сигналов и помех
Модуль ИС состоит из операторов, в результате выполнения которых вырабатывается значение информационного символа, имеющего случайный характер Далее следует модуль передатчика.

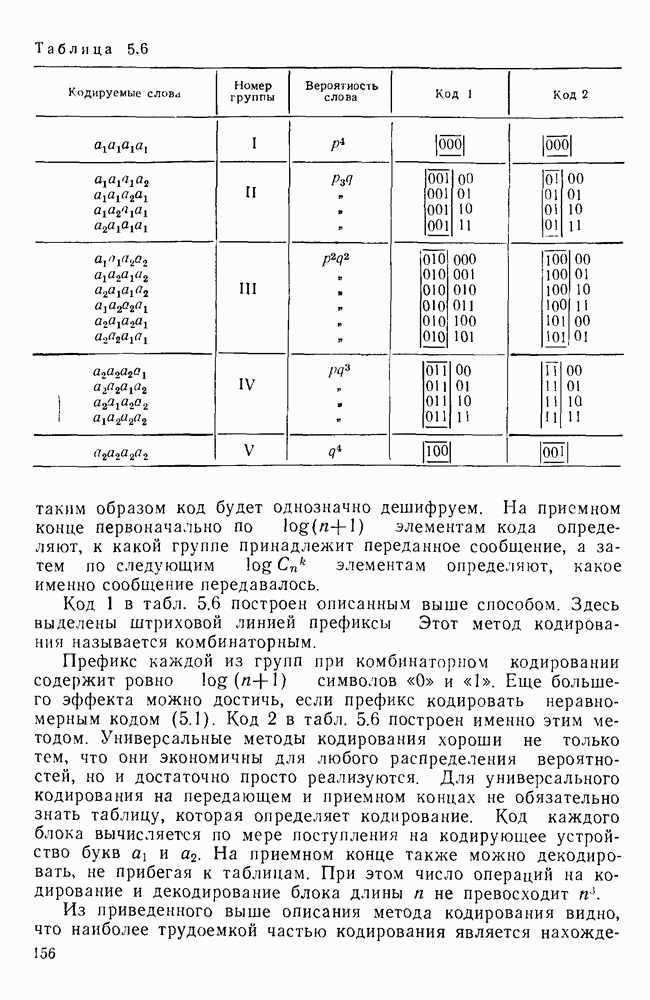
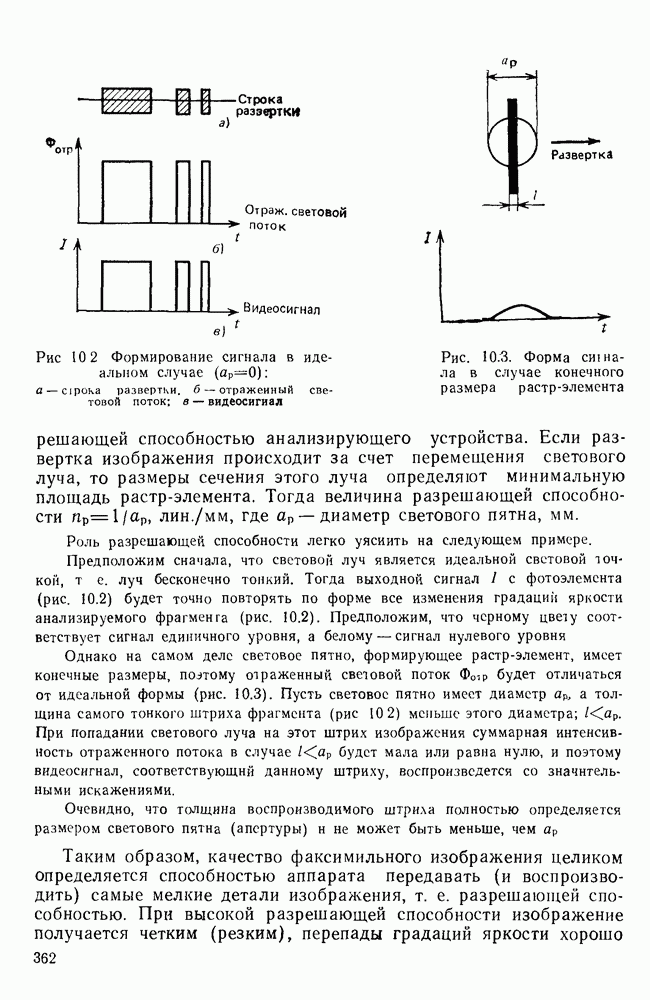
Рис. П. 1.3. Плотность распределения вероятности 
Операторы, входящие в этот модуль, формируют отсчеты модулированного сигнала, соответствующие выработанному информационному символу, и принятым виду модуляции и помехоустойчивому коду (если он используется)
Модуль источника помех включает в себя операторы, вырабатывающие случайные значения отсчетов, втияиие которых на качество передачи информации исследуется в данной модели системы ПДС
Модуль каната связи реализует математические операции, в результате которых сигналы передатчика искажаются вследствие неидеальности частотных характеристик канала и наложения отсчетов помех на отсчеты сшнала Если помеха мультипликативная, например, типа занижения уровня сигиала, то отсчеты мультипликативном помехи перемножаются с соответствующими отсчетами сигнала
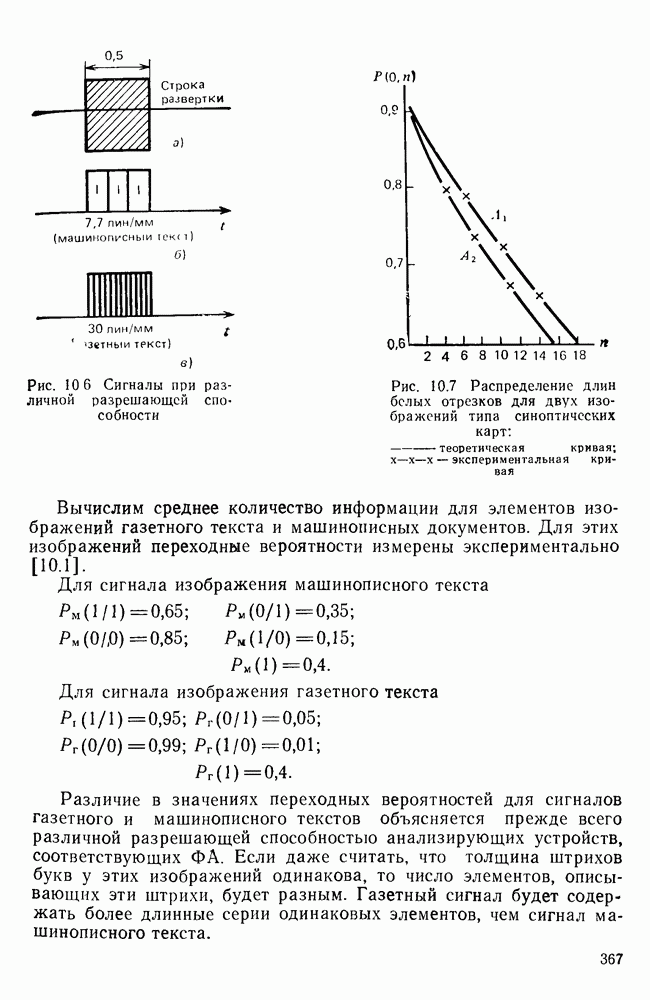
Модуль приемника содержит операторы, реализующие операции фильтрации, демодуляции и декодирования Информационный символ с выхода приемника поступает в логический блок, где он сравнивается с переданным символом Если при  испытании символы не совпадают, величине ошибки а, приписывается значение 1 в противном случае — 0 Соответственно в счетчик ошибок добавляется либо
испытании символы не совпадают, величине ошибки а, приписывается значение 1 в противном случае — 0 Соответственно в счетчик ошибок добавляется либо  либо
либо 
Да  осуществляется увеличение содержимого счетчика числа испытаний на единицу После этого текущее число испытаний сравнивается с заданным числом
осуществляется увеличение содержимого счетчика числа испытаний на единицу После этого текущее число испытаний сравнивается с заданным числом  Если текущее число испытаний оказывается меньше
Если текущее число испытаний оказывается меньше  управление выполнением программы передается в начало программы и начинается новый цикл испытания. В противном случае рассчитывается оценка вероятности ошибки
управление выполнением программы передается в начало программы и начинается новый цикл испытания. В противном случае рассчитывается оценка вероятности ошибки  которая выводится на печать Работа программы на этом заканчивается
которая выводится на печать Работа программы на этом заканчивается
Определение числа испытаний  Исходя из самого определения вероятности, значение
Исходя из самого определения вероятности, значение  можно получить лишь при бесконечно большом числе испытаний, что практически невозможно При ограничении числа испытаний некоторой величиной
можно получить лишь при бесконечно большом числе испытаний, что практически невозможно При ограничении числа испытаний некоторой величиной  вместо значения
вместо значения  получают оценку вероятности ошибки
получают оценку вероятности ошибки  являющуюся случайным числом Как любое случайное число,
являющуюся случайным числом Как любое случайное число,  характеризуется плотностью вероятности
характеризуется плотностью вероятности  дисперсией
дисперсией  и математическим ожиданием
и математическим ожиданием  которое равно
которое равно  При достаточно большом числе испытаний
При достаточно большом числе испытаний  можно считать случайной величиной, имеющей нормальный закон распределения
можно считать случайной величиной, имеющей нормальный закон распределения
Выбор числа испытаний зависит от того, какие требования предъявляются к точности определения  Точность оценки
Точность оценки  зададим шириной доверительного интервала
зададим шириной доверительного интервала  который определим следующим образом
который определим следующим образом 
Определение необходимого числа испытаний  для получения оценки вероятности ошибки с необходимой точностью
для получения оценки вероятности ошибки с необходимой точностью  и доверительной вероятностью
и доверительной вероятностью  можно произвести с помощью известного из теории вероятностей выражения, которое для рассматриваемой задачи примет вид
можно произвести с помощью известного из теории вероятностей выражения, которое для рассматриваемой задачи примет вид

Здесь  — функция Крампа, значения которой табулированы
— функция Крампа, значения которой табулированы
Очевидно, что вначале используя таблицы значений функции Крампа, по величине  необходимо найти аргумент функции
необходимо найти аргумент функции  Пусть его значение равно
Пусть его значение равно  Тогда можно записать
Тогда можно записать  откуда
откуда

Теперь остается найти дисперсию 
Как уже говорилось выше, в рассматриваемой задаче можно считать, что итогом каждого  испытания модели системы ПДС будет случайная величина
испытания модели системы ПДС будет случайная величина  являющаяся результатом сравнения переданного информационного символа с принятым При их несовпадениеи
являющаяся результатом сравнения переданного информационного символа с принятым При их несовпадениеи  (ошибка), а при совпадении
(ошибка), а при совпадении  (нет ошибки),
(нет ошибки),  случайная величина а, может принимать только два значения
случайная величина а, может принимать только два значения  с вероятностью
с вероятностью  с вероятностью
с вероятностью  Следовательно, математическое ожидание
Следовательно, математическое ожидание

Тогда согласно определению дисперсии

Подставляя последнее выражение в  получим
получим

где  — относительная погрешность определения
— относительная погрешность определения 
Поскольку значение  лишь подлежит определению, то для нахождения числа испытании поступают следующим образом Выбирают вначале число испы таний (100 200), по результатам этих испытаний определяют грубую оценку вероятности ошибки, которую подставляют в формулу
лишь подлежит определению, то для нахождения числа испытании поступают следующим образом Выбирают вначале число испы таний (100 200), по результатам этих испытаний определяют грубую оценку вероятности ошибки, которую подставляют в формулу  в качестве
в качестве  После этого вычисляют окончательное значение
После этого вычисляют окончательное значение 
Из  следует, что число испытаний существенно зависит от величины оцениваемой вероятности ошибки Поэтому целесообразно так строить модели рующий алгоритм или так выбирать исходные данные, чтобы вероятность ошибки была не очень близка к нулю во избежание значительного увеличения необходимого числа испытаний
следует, что число испытаний существенно зависит от величины оцениваемой вероятности ошибки Поэтому целесообразно так строить модели рующий алгоритм или так выбирать исходные данные, чтобы вероятность ошибки была не очень близка к нулю во избежание значительного увеличения необходимого числа испытаний
Проиллюстрируем сказанное примером Пусть необходимо наити число испытаний для оценки вероятности ошибки с точностью  и доверительной вероятностью 0,9 Грубая оценка вероятности ошибки, полученная в результате пробных испытаний, равна 0,1
и доверительной вероятностью 0,9 Грубая оценка вероятности ошибки, полученная в результате пробных испытаний, равна 0,1
Вначале по заданной доверительной вероятности с помощью таблицы  чений функции Крампа определяем верхний предел интегрирования
чений функции Крампа определяем верхний предел интегрирования  который в данном случае равен 1,65
который в данном случае равен 1,65
Подставляя в  числовые значения, получим
числовые значения, получим  При уменьшении вероятности ошибки в 10 и 100 раз необходимое число испытаний достигает соответственно значений 2703 и 27273.
При уменьшении вероятности ошибки в 10 и 100 раз необходимое число испытаний достигает соответственно значений 2703 и 27273.
Конкретные вопросы моделирования отдельных блоков системы ПДС рассмотрены ниже
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
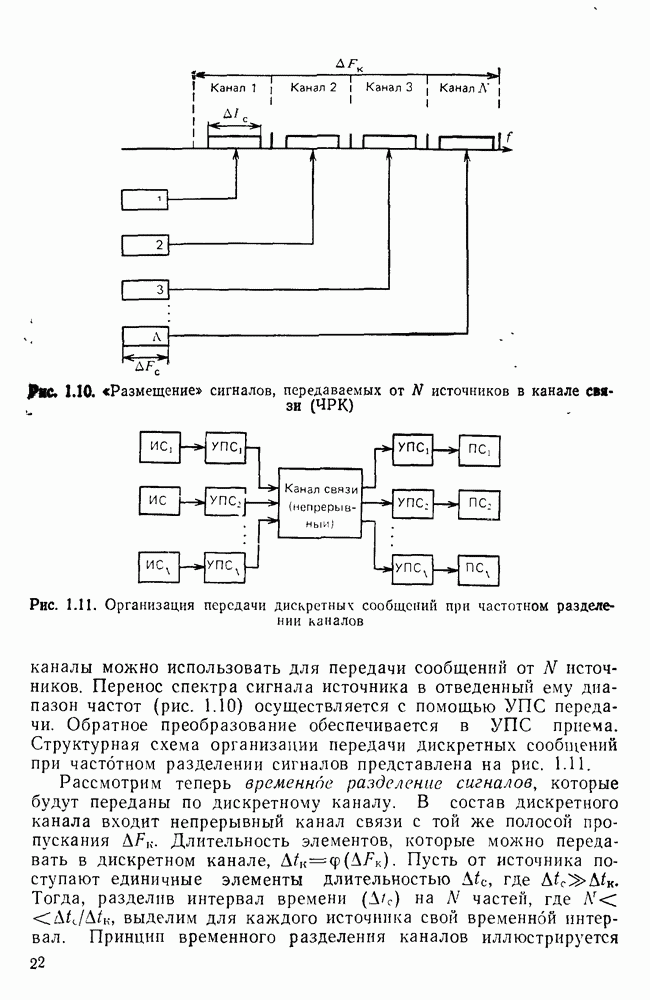
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
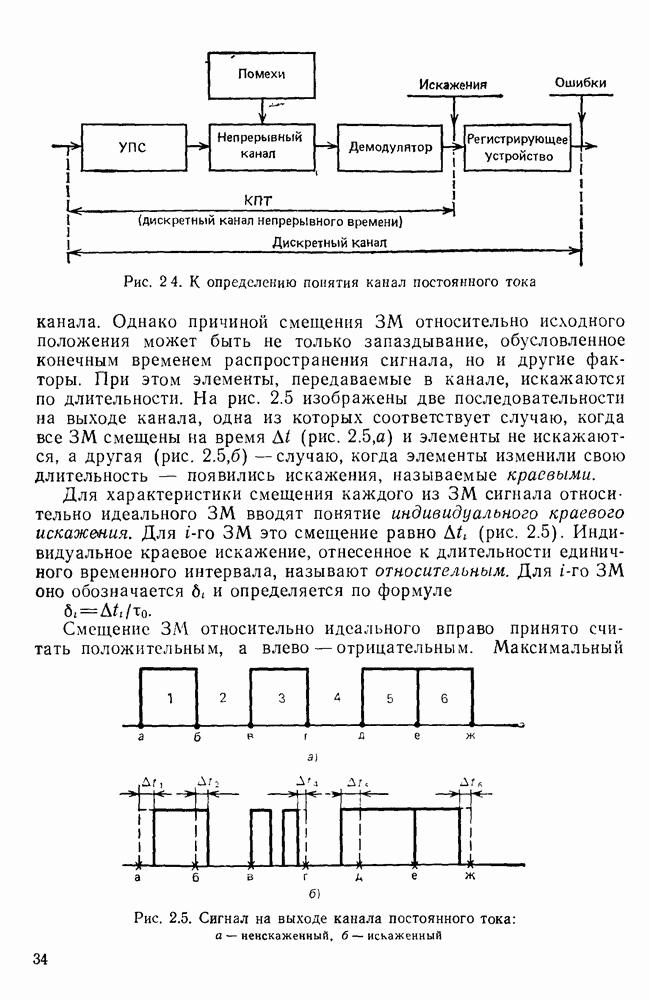
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
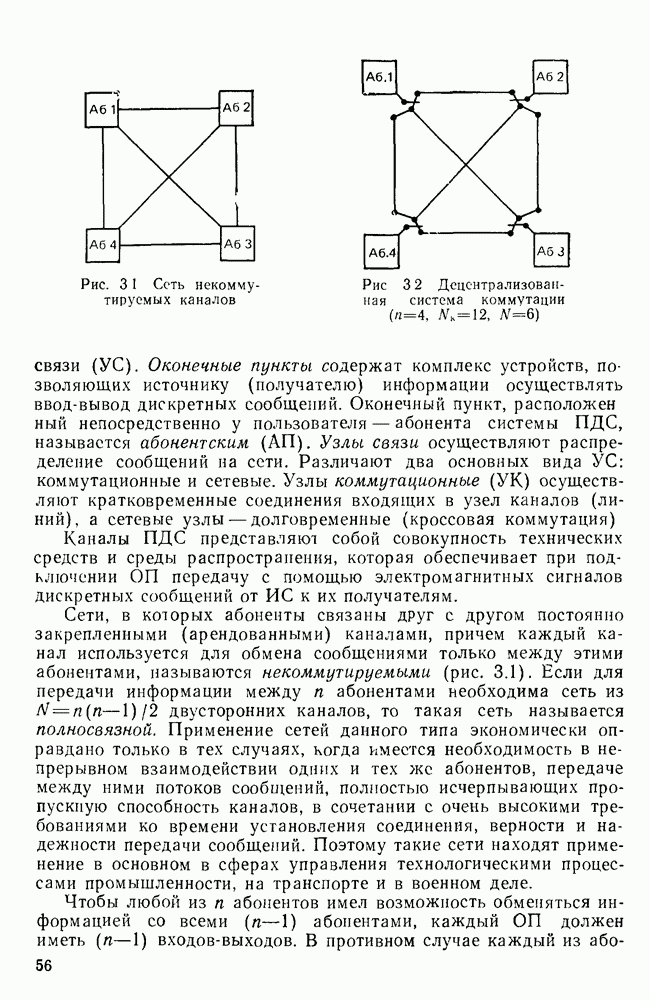
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
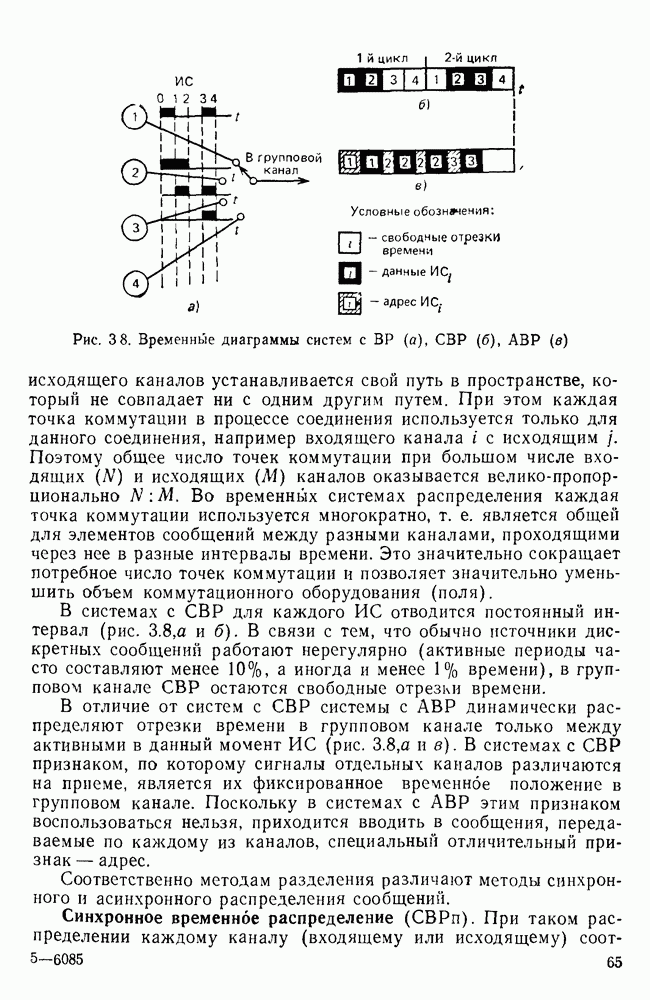
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
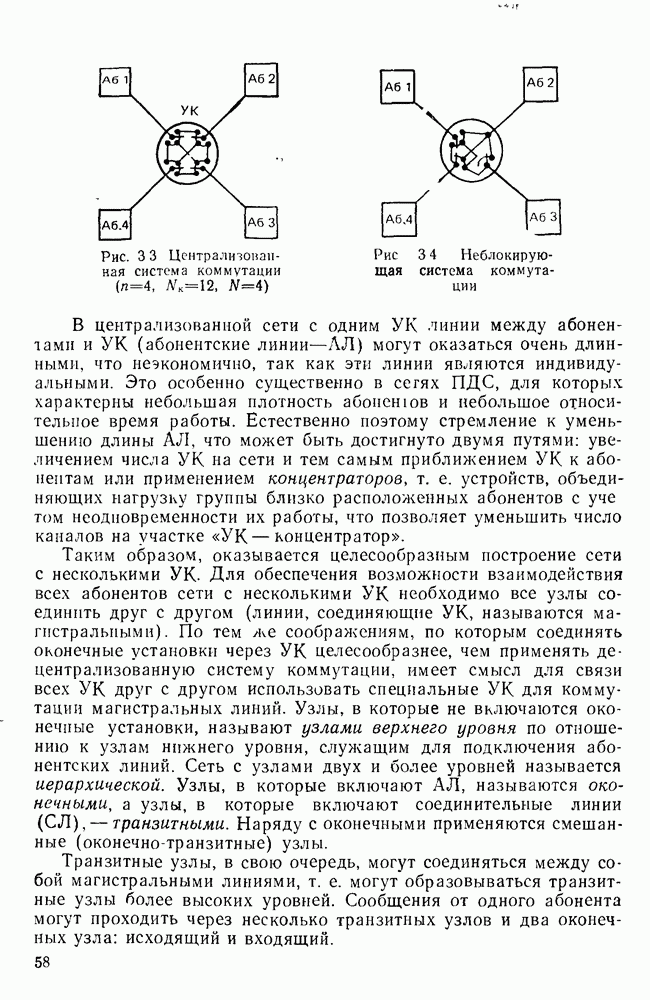
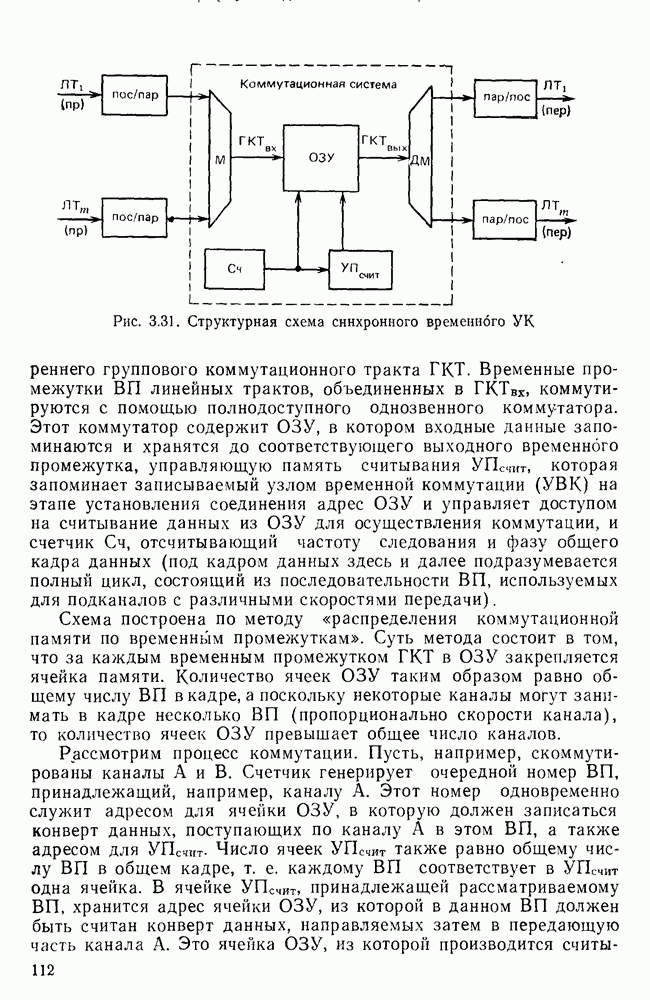
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
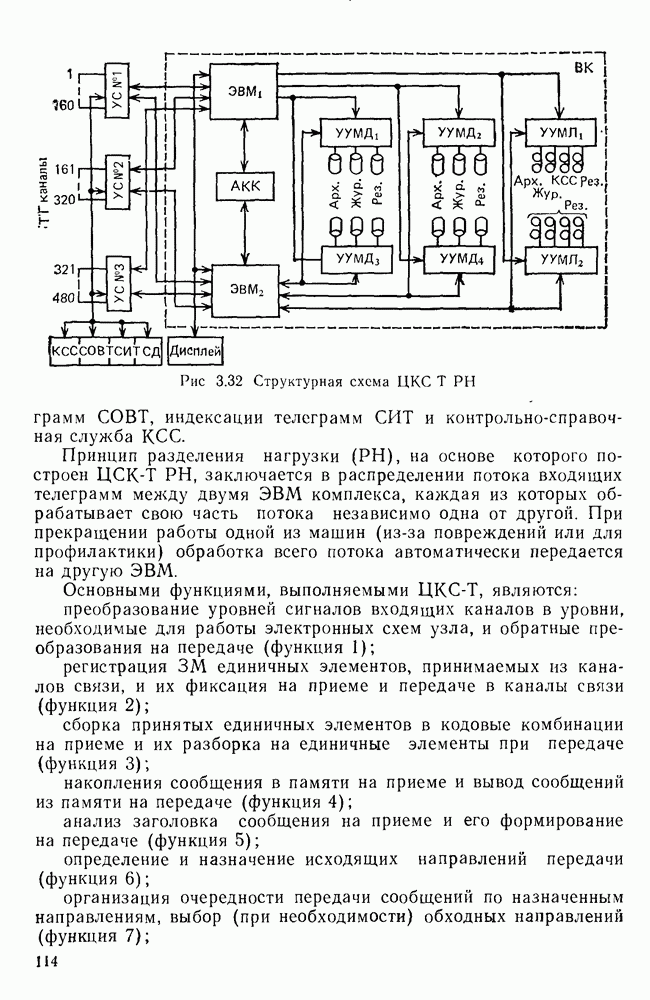
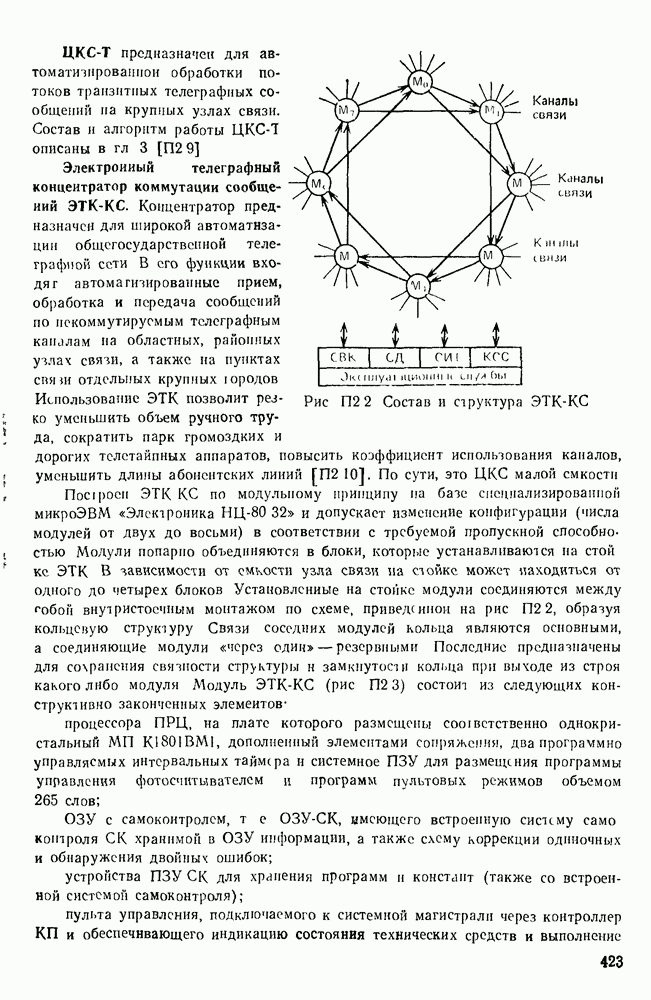
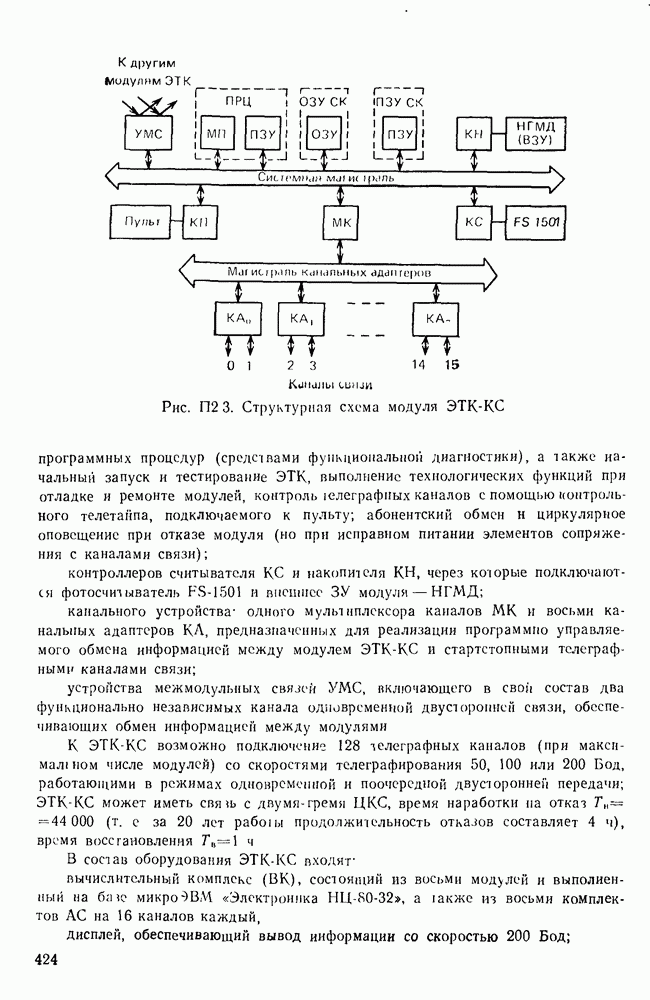
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
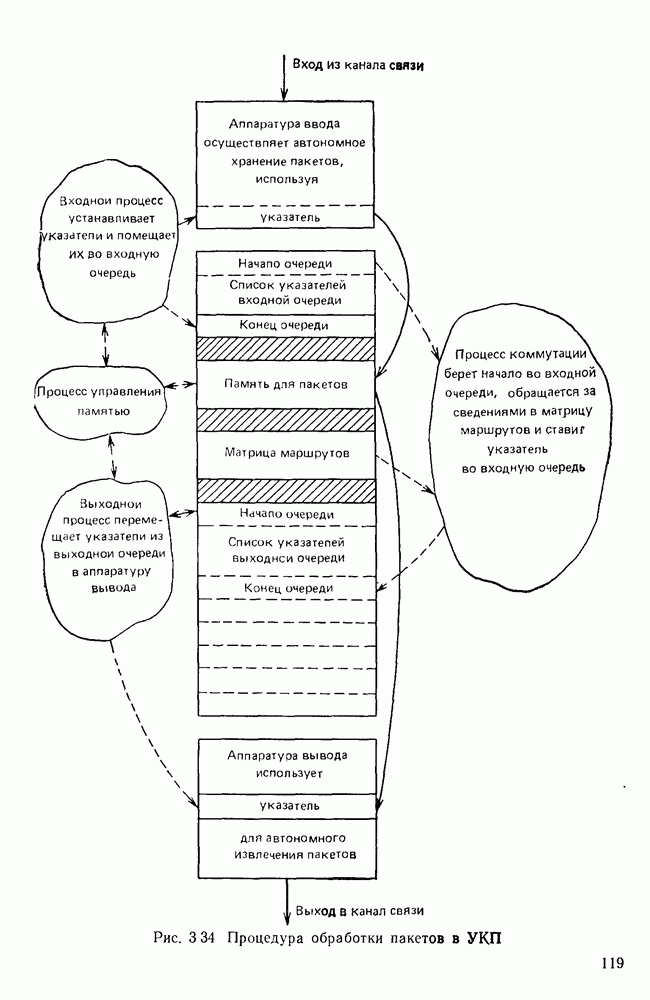
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
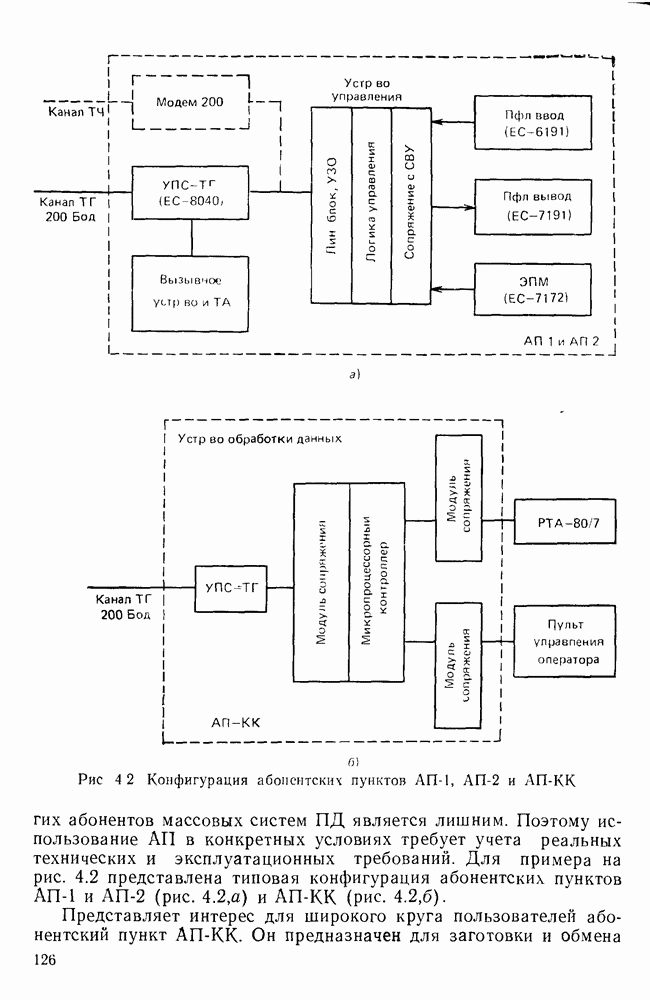
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
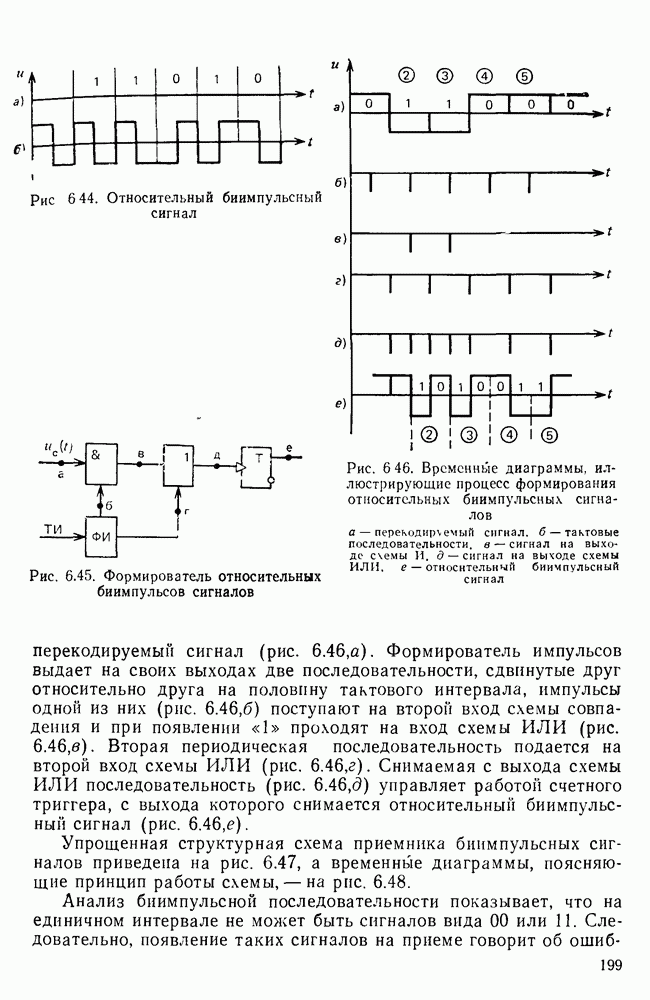
- Модулированные сигналы.
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
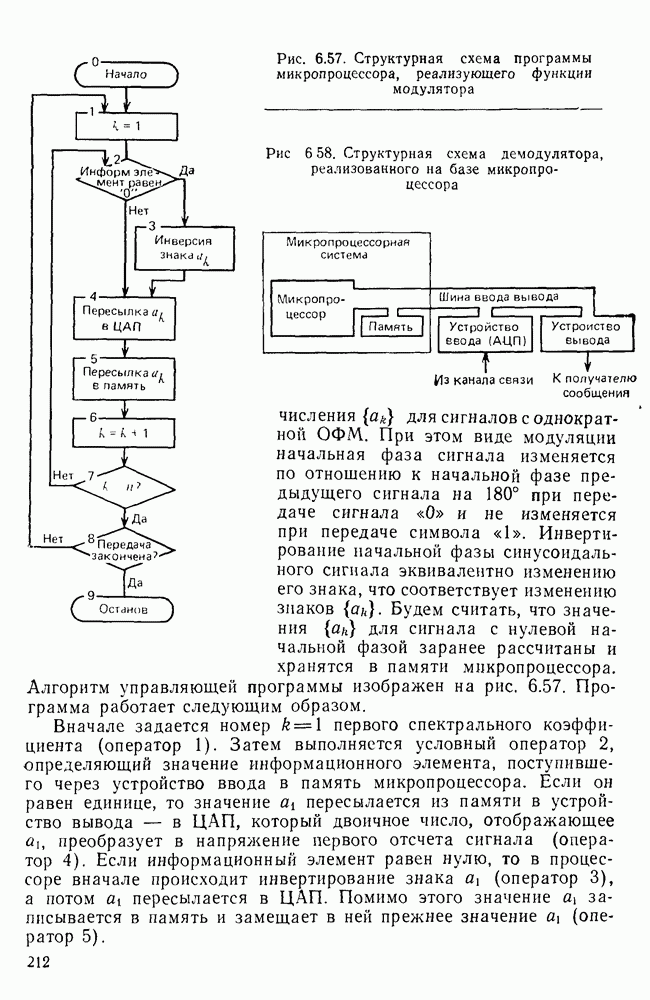
- Основы микропроцессорной реализации модуляторов УПС.
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
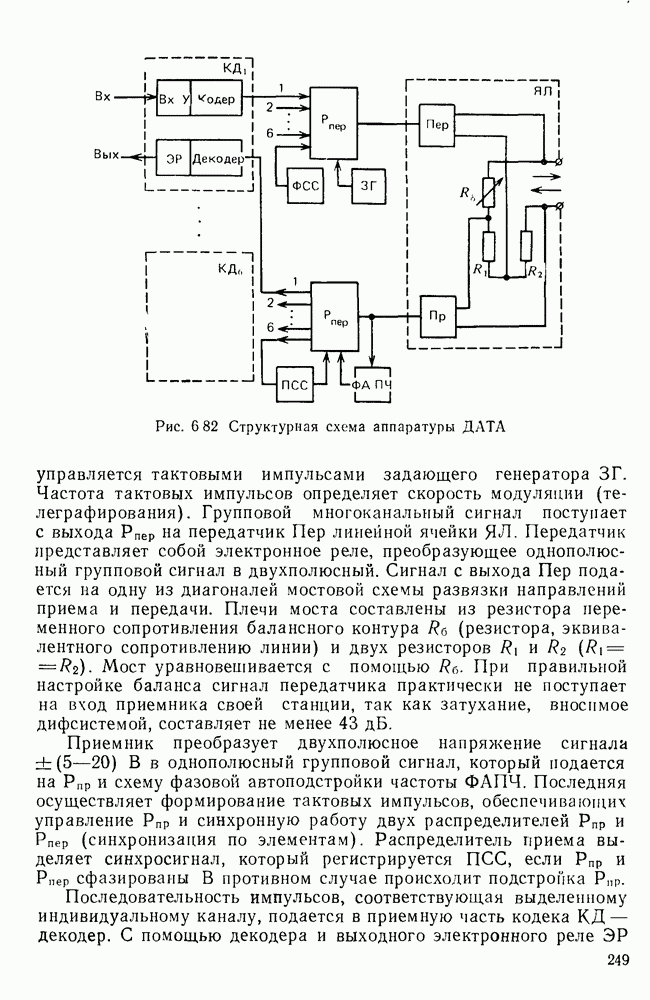
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
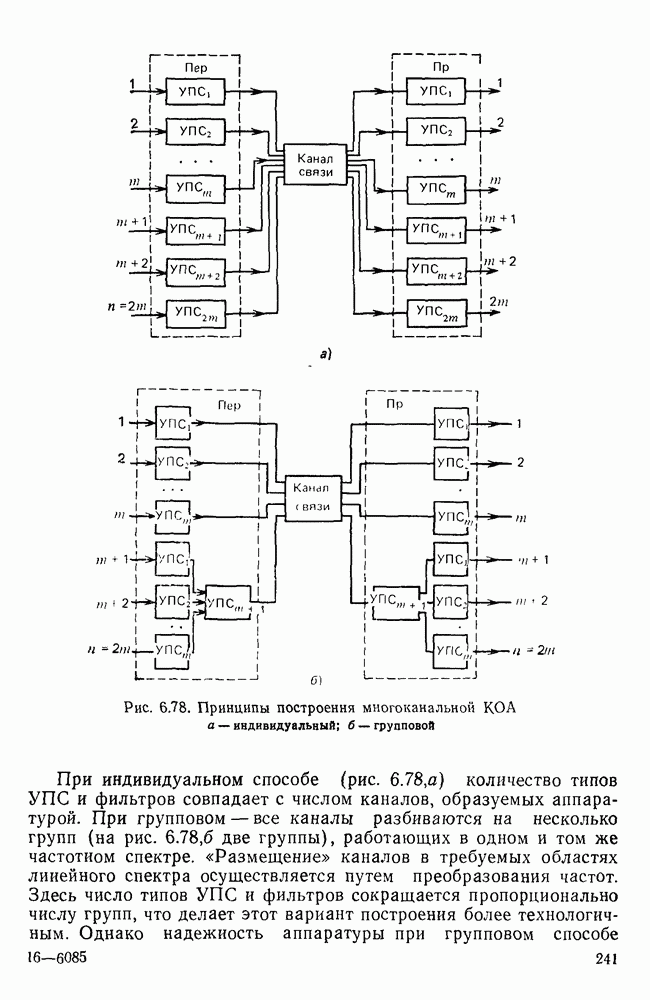
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
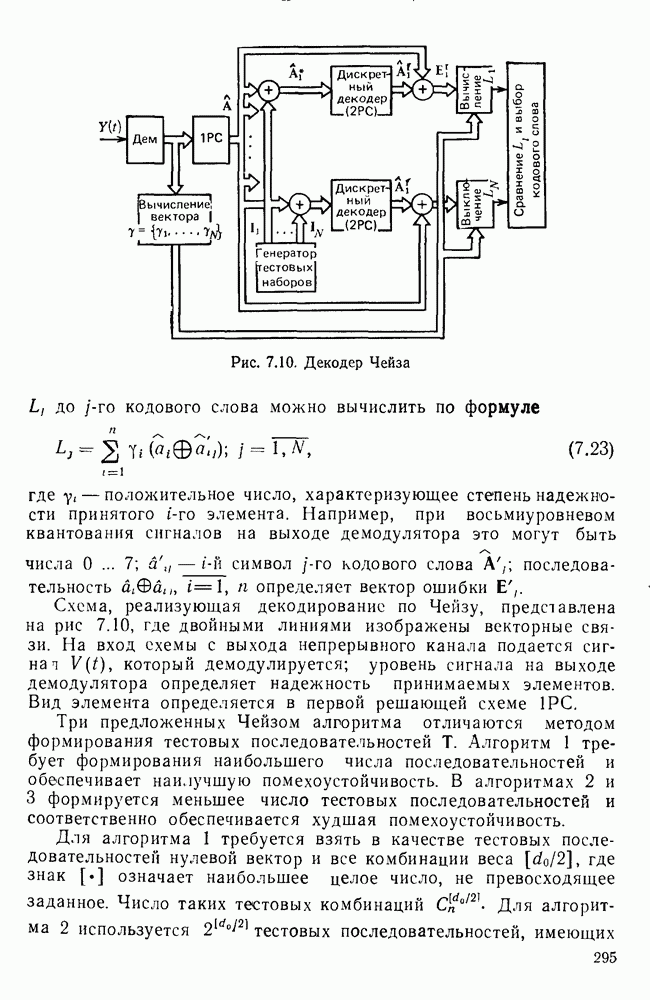
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
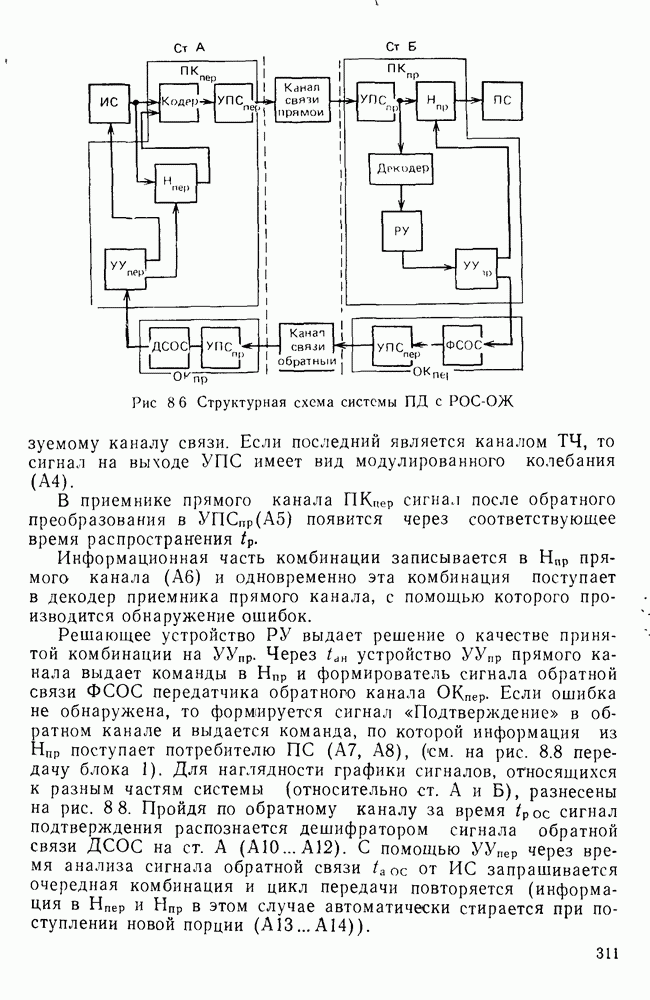
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
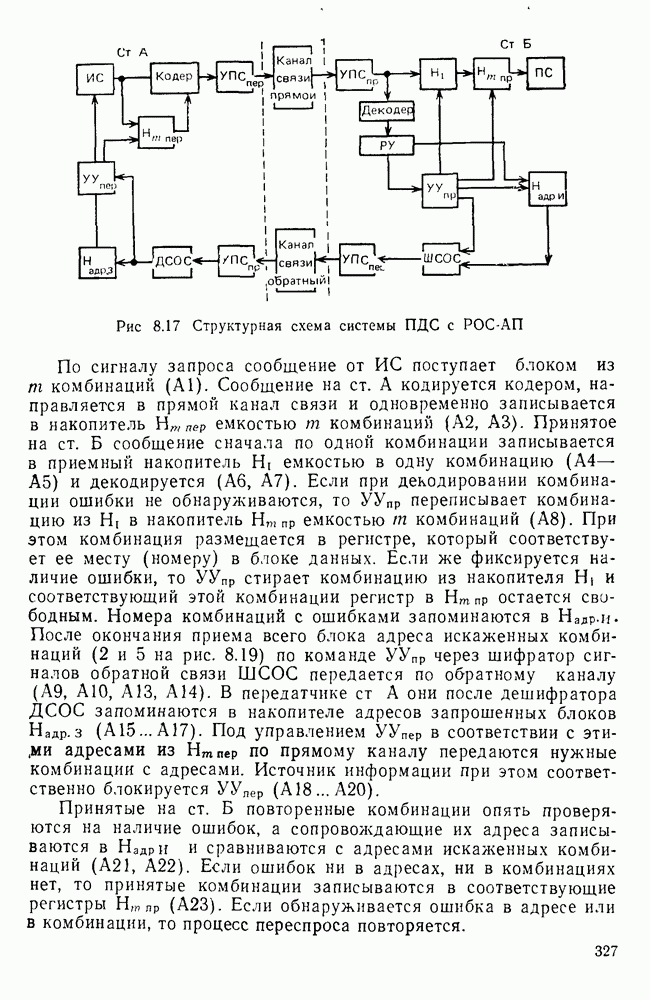
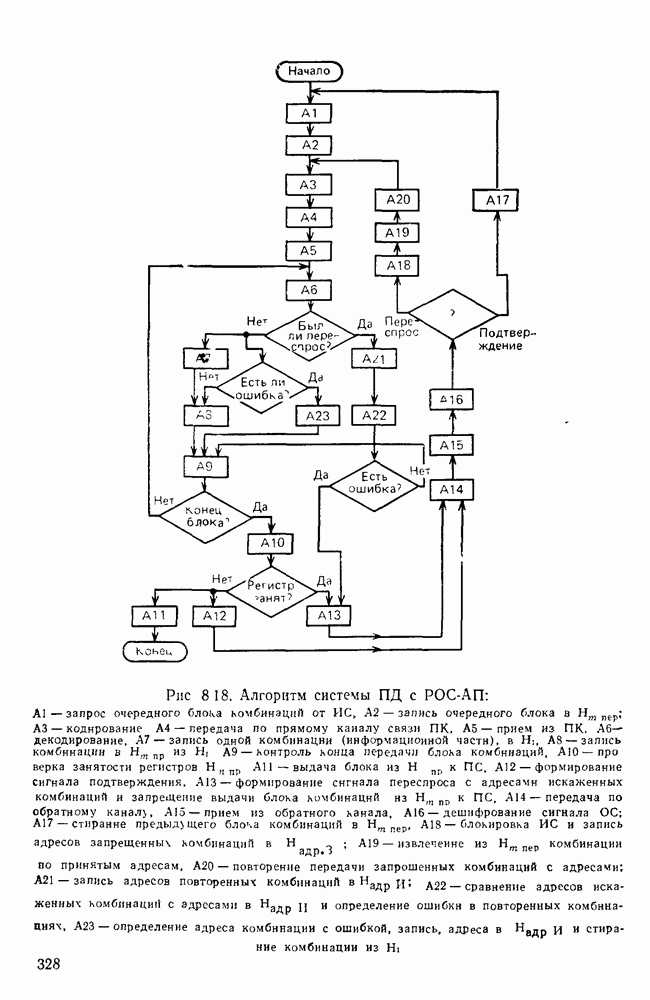
- Система с РОС и адресным переспросом РОС-АП.
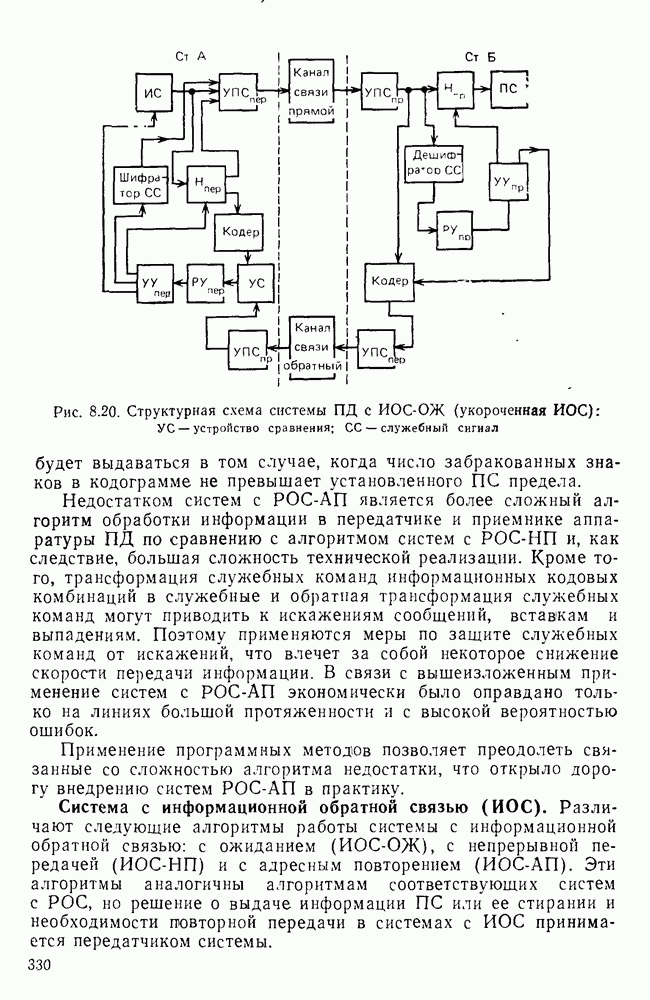
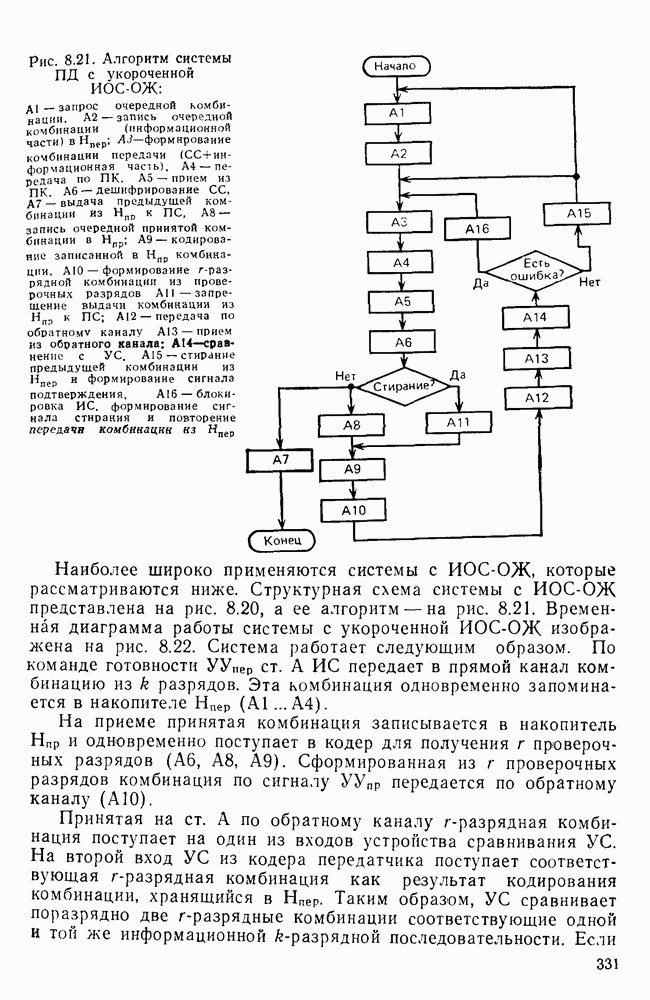
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ