| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
7.1. ЛИНЕЙНЫЕ КОДЫ
Построение линейных кодов. В гл 2 простой трехэлементный код был задан перечислением всех кодовых комбинаций (см. табл. 2 1) Данное множество можно рассматривать как некоторую алгебраическую систему, которая называется группой с заданной на ней операцией сложения по модулю два [7 1]. Рассмотрим в общем виде основные свойства такого множества Обычно группа обозначается буквой G, а элементы множества g, На этом множестве задана некоторая групповая операция, которую обозначим символом «0» Эта операция однозначно сопоставляет двум элементам  и g, множества G, третий элемент того же множества
и g, множества G, третий элемент того же множества  где
где  . Обычно говорят, что группа является замкнутой относительно операции
. Обычно говорят, что группа является замкнутой относительно операции 
Множество G с определенной на нем групповой операцией  называется группой, если выполняются следующие условия,
называется группой, если выполняются следующие условия,
1. Ассоциативность (сочетательность) - для любых трех элементов группы, например  .
.

2. Существование нейтрального элемента: среди элементов множества имеется некоторый элемент  , называемый нейтральным, такой, что
, называемый нейтральным, такой, что

для всех i.
3. Существование обратного элемента для каждого данного элемента; к каждому элементу  можно подобрать такой элемент
можно подобрать такой элемент  , что
, что

Группа, в которой выполняется также условие  для всех I, j, называется коммутативной, или абелевой, группой. Группа называется конечной, если она состоит из конечного числа элементов. В противном случае она называется бесконечной.
для всех I, j, называется коммутативной, или абелевой, группой. Группа называется конечной, если она состоит из конечного числа элементов. В противном случае она называется бесконечной.
Пример 7.1. Задав в качестве групповой операции операцию сложения по модулю 2, убедимся, что множество 000, 001, 010, 100, 110, 011, 101, 111 является группоп Складывая элементы множества в различном сочетании, видим, что каждый раз получаем элемент, входящий в множество Так, 001  и т. п. Нетрудно заметить, что условие ассоциативности также выполняется Нейтральным является элемент 000 Для каждого элемента, заданного в примере множества, существует обратный Так, для элемента 100 обратным является он сам, т. е.
и т. п. Нетрудно заметить, что условие ассоциативности также выполняется Нейтральным является элемент 000 Для каждого элемента, заданного в примере множества, существует обратный Так, для элемента 100 обратным является он сам, т. е.

Таким образом, рассматриваемое множество является группой, порядок которой (число элементов) равен восьми Очевидно также, что данная группа является коммутат ивной
Пример 7.2. Задавшись в качестве групповой операции операцией умножения, рассмотрим множество рациональных чисел
Перемножая элементы множества в различном сочетании, получаем рациональное число Легко убедиться в том, что выполняется условие ассоциативности Нейтральным элементом, очевидно, является единица Для каждого элемента заданного рациональным числом, имеется ему обратный Так, для числа 2 это 1/2, числа 1/4 — это 4 и т. д.
Множество элементов примера  не обязательно задавать перечислением всех элементов, входящих в группу
не обязательно задавать перечислением всех элементов, входящих в группу
Пользуясь свойством замкнутости относительно операции сложения по модулю 2, такое множество можно задать матрицей

Все остальные элементы группы (кроме 000) могут быть получены путем сложения по модулю 2 различных сочетаний строк матрицы (7.1). Матрица (7.1) называется производящей матрицей рассмотренного в примере 7.1 трехэлементного кода. Кодовые комбинации, составляющие матрицу (7.1), являются линейно-независимыми.
Можно было бы составить матрицу и из других линейно-независимых кодовых комбинаций. Напомним, что ненулевые комбинации  являются линейно-независимыми, если
являются линейно-независимыми, если  при условии, что хотя бы один из коэффициентов
при условии, что хотя бы один из коэффициентов 
Код, заданный матрицей (7.1), является линейным, т. е. имеет структуру, обладающую свойством линейности. Двоичный блочный код является линейным тогда и только тогда, когда сумма по модулю 2 двух кодовых слов является также кодовым словом [7.1]. Двоичные линейные коды называют также групповыми.
Так как в системе ПДС используются, как правило, корректирующие коды, перейдем далее к рассмотрению линейных (групповых) корректирующих кодов и поиску кодов с заданным алфавитом передаваемых сообщений и кодовым расстоянием  которые позволят обеспечить требуемую верность.
которые позволят обеспечить требуемую верность.
Пример 7.3. Пусть требуется построить линейный код с  для передачи восьми сообщений
для передачи восьми сообщений
Тогда необходимое число информационных элементов  Запишем исходный код в виде единичной матрицы (7 1) и дополним информационные элементы элементами, которые в дальнейшем будем называть проверочными, так, чтобы обеспечить
Запишем исходный код в виде единичной матрицы (7 1) и дополним информационные элементы элементами, которые в дальнейшем будем называть проверочными, так, чтобы обеспечить  Дополним каждую строку матрицы (7.1) двумя элементами
Дополним каждую строку матрицы (7.1) двумя элементами

Складывая по модулю 2 строки матрицы (7 2), видим, что хэммиигово расстояние для 1,2, 1,3; 2,3 строк равно 3 Однако при этом кодовое расстояние, равное 3, не обеспечивается, так как в числе разрешенных кодовых комбинации (множества, являющегося группой) имеется нейтральный элемент 00000, относительно которого комбинации 10010 и 01001 имеют хэммингово расстояние, равное только двум.
Таким образом, производящая матрица  матрица кода (5 3) с кодовым расстоянием, равным только двум. Для получения
матрица кода (5 3) с кодовым расстоянием, равным только двум. Для получения  необходимо к исходным информационным элементам добавить проверочные элементы, в числе которых было бы не мепее двух единиц, а добавляемые проверочные элементы разных строк отличались бы, по крайней мере, в одном элементе Этому требованию удовлетворяет производящая матрица
необходимо к исходным информационным элементам добавить проверочные элементы, в числе которых было бы не мепее двух единиц, а добавляемые проверочные элементы разных строк отличались бы, по крайней мере, в одном элементе Этому требованию удовлетворяет производящая матрица

Добавляемые проверочные элементы могут быть записаны и в другом порядке. Необходимо лишь обеспечить  Матрица (7 3) является производящей, или порождающей, матрицей кода (6 3), содержащею
Матрица (7 3) является производящей, или порождающей, матрицей кода (6 3), содержащею  элементов, из которых три информационных. Обычно матрицу обозначают буквой G с индексом, указывающим, к какому коду она относится (в нашем случае
элементов, из которых три информационных. Обычно матрицу обозначают буквой G с индексом, указывающим, к какому коду она относится (в нашем случае  ).
).
Производящая матрица состоит из двух матриц: единичной размерности  и матрицы
и матрицы  содержащей k строк и
содержащей k строк и  столбцов. В строке матрицы Скуг должно быть не менее, чем
столбцов. В строке матрицы Скуг должно быть не менее, чем  единиц, а хзммингово расстояние между строками не менее чем
единиц, а хзммингово расстояние между строками не менее чем  Очевидно также, что общее число элементов в строке матрицы
Очевидно также, что общее число элементов в строке матрицы  должно определяться неравенством
должно определяться неравенством 
Обозначим элементы комбинаций кода, задаваемого матрицей (7.3),  , где
, где  — информационные, а
— информационные, а  — проверочные элементы. Полученный линейный код является систематическим
— проверочные элементы. Полученный линейный код является систематическим  Проверочные элементы могут быть получены путем суммирования по модулю 2 определенных информационных элементов. Найдем это правило для
Проверочные элементы могут быть получены путем суммирования по модулю 2 определенных информационных элементов. Найдем это правило для  пользуясь матрицей (7.3). Из первой строки следует, что в суммировании обязательно должен участвовать элемент
пользуясь матрицей (7.3). Из первой строки следует, что в суммировании обязательно должен участвовать элемент  (только в этом случае
(только в этом случае  ). Из второй строки следует, что элемент
). Из второй строки следует, что элемент  в суммировании не должен участвовать. Из третьей строки следует, что элемент
в суммировании не должен участвовать. Из третьей строки следует, что элемент  должен участвовать в суммировании. Итак,
должен участвовать в суммировании. Итак,

Уравнения для  записываются в виде
записываются в виде

Представим правила (7.4) -(7.6) в виде матрицы  называемой проверочной. Эта матрица содержит
называемой проверочной. Эта матрица содержит  строк и k столбцов:
строк и k столбцов:

Каждая из  строк матрицы (7.7) определяет правило формирования соответствующего проверочного элемента. Так, единицы, расположенные на местах, соответствующих информационным элементам в первой строке, указывают на то, какие информационные элементы должны участвовать в получении первого проверочного элемента (элемента 04). Единица на месте, соответствующем проверочному элементу (четвертом месте), указывает, какой проверочный элемент получается в результате суммирования информационных элементов. Так, из первой строки следует
строк матрицы (7.7) определяет правило формирования соответствующего проверочного элемента. Так, единицы, расположенные на местах, соответствующих информационным элементам в первой строке, указывают на то, какие информационные элементы должны участвовать в получении первого проверочного элемента (элемента 04). Единица на месте, соответствующем проверочному элементу (четвертом месте), указывает, какой проверочный элемент получается в результате суммирования информационных элементов. Так, из первой строки следует  Матрица
Матрица  состоит из двух матриц: прямоугольной
состоит из двух матриц: прямоугольной  и единичной b, содержащей
и единичной b, содержащей  строк и
строк и  столбцов:
столбцов:

Легко заметить, что  означает транспонирование)
означает транспонирование)
Проверочная матрица задает правила кодирования линейного кода и определяет схему кодирующего устройства. Структурная схема кодирующего устройства, задаваемого проверочной матрицей  приведена на рис. 7.1. Запишите
приведена на рис. 7.1. Запишите 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
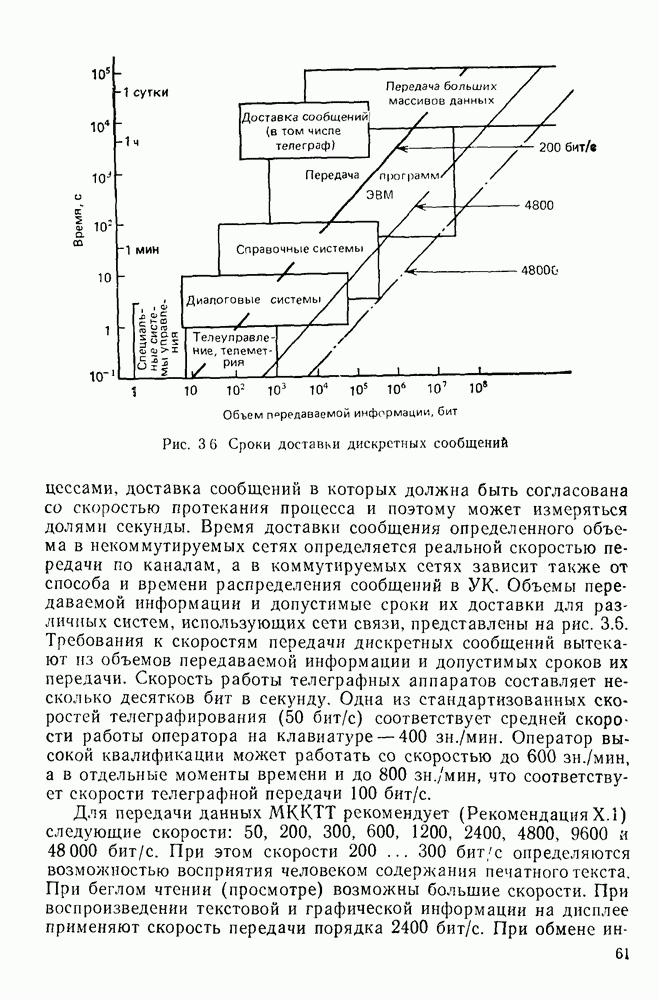
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
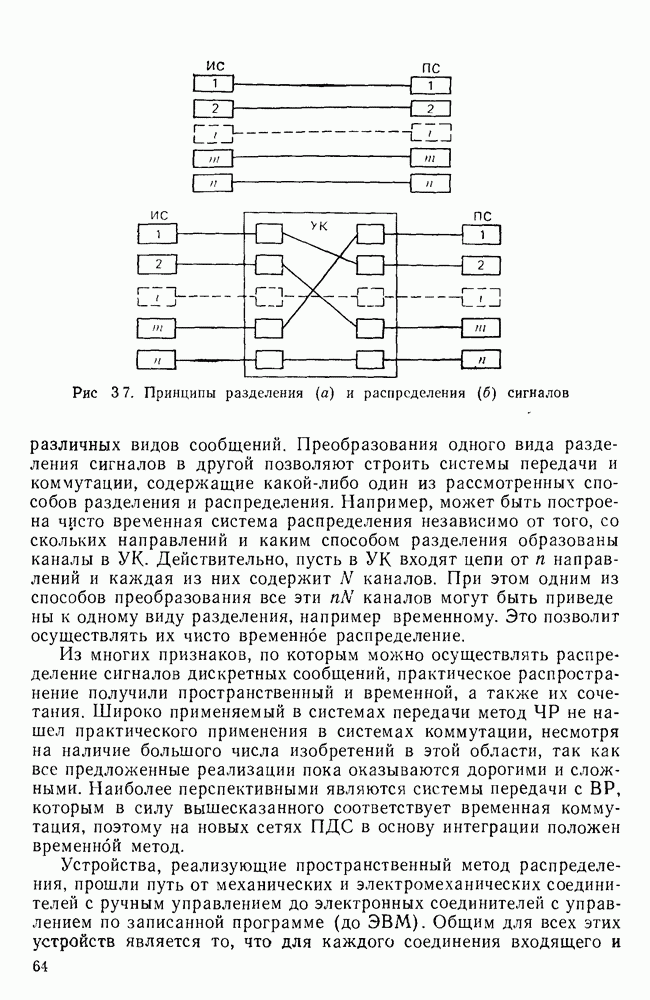
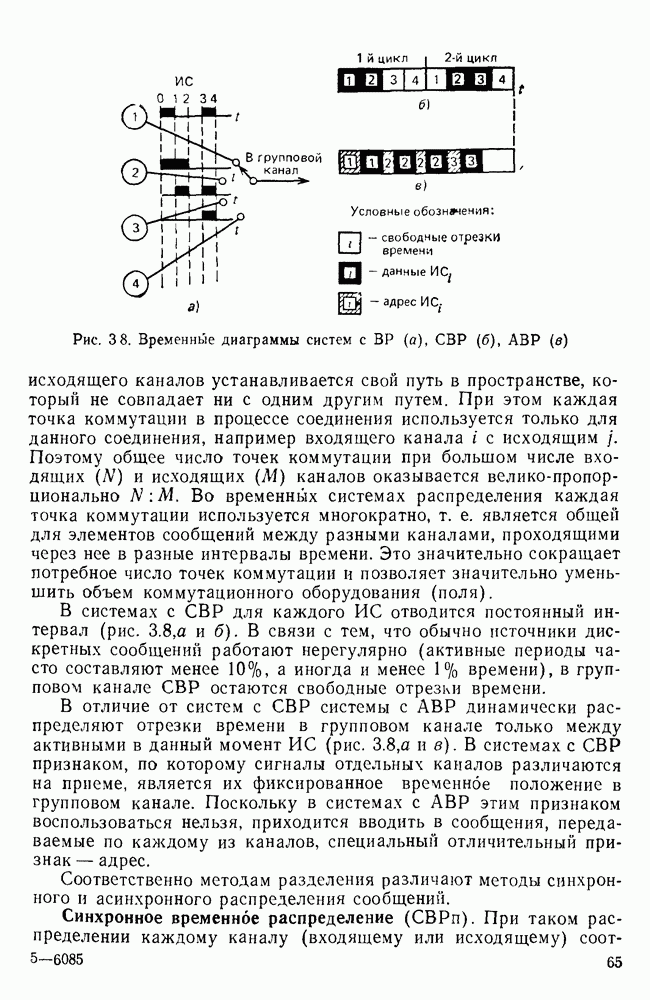
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
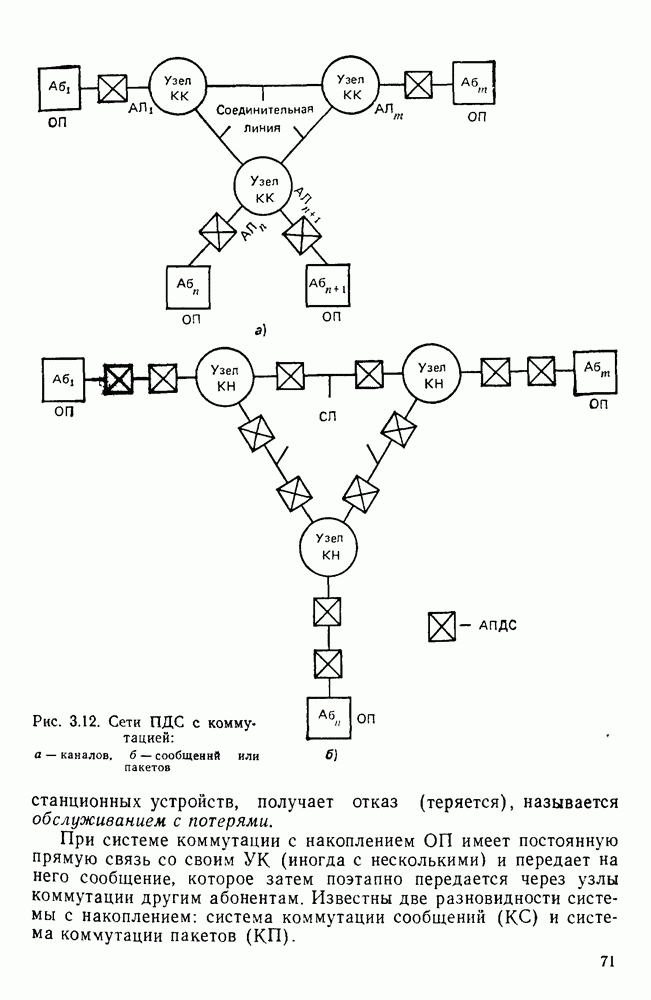
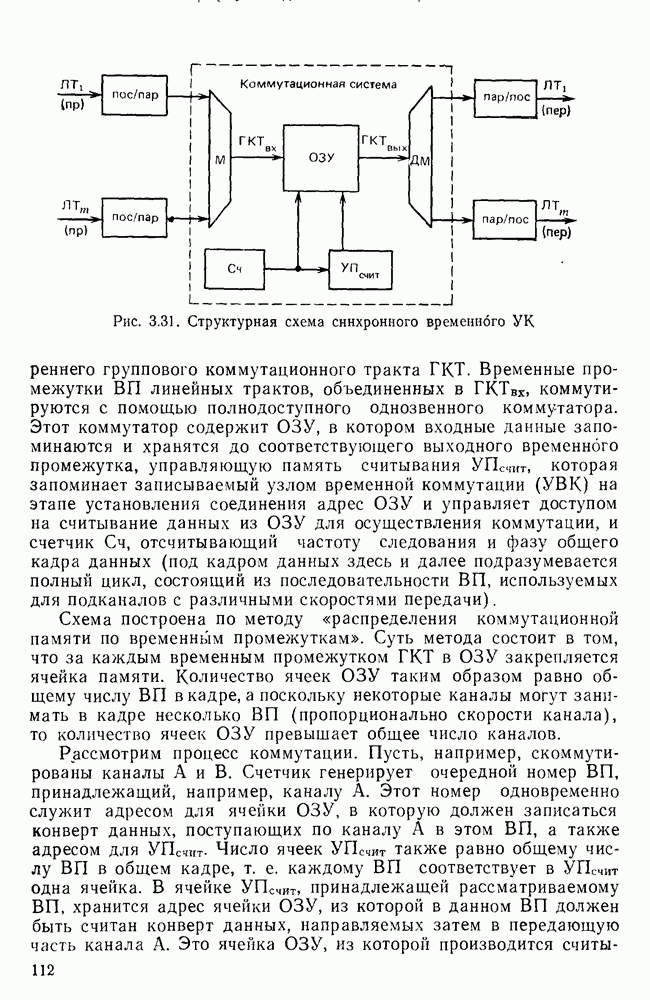
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
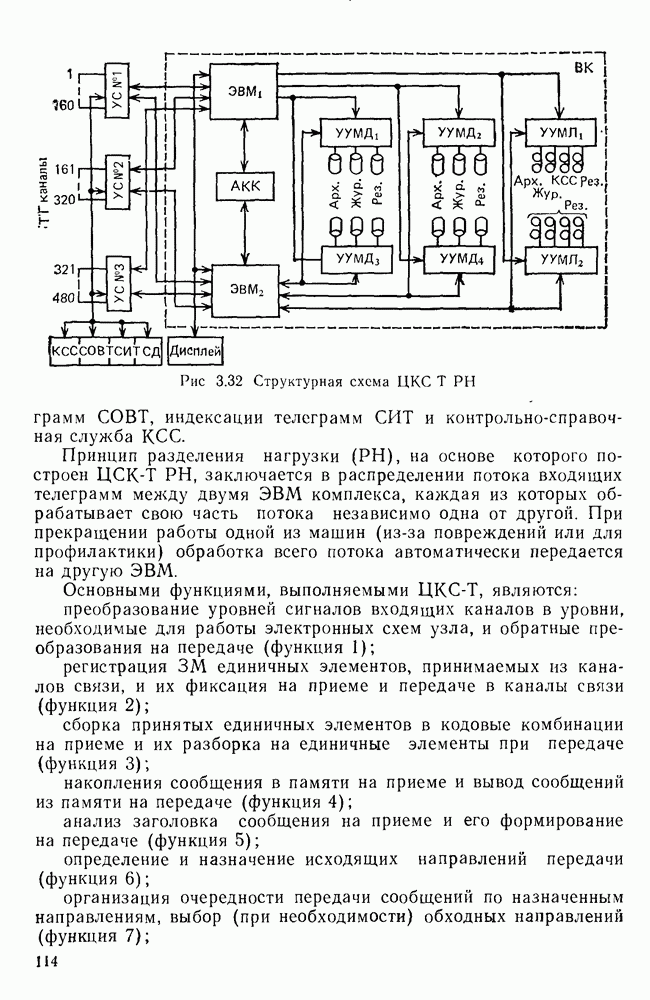
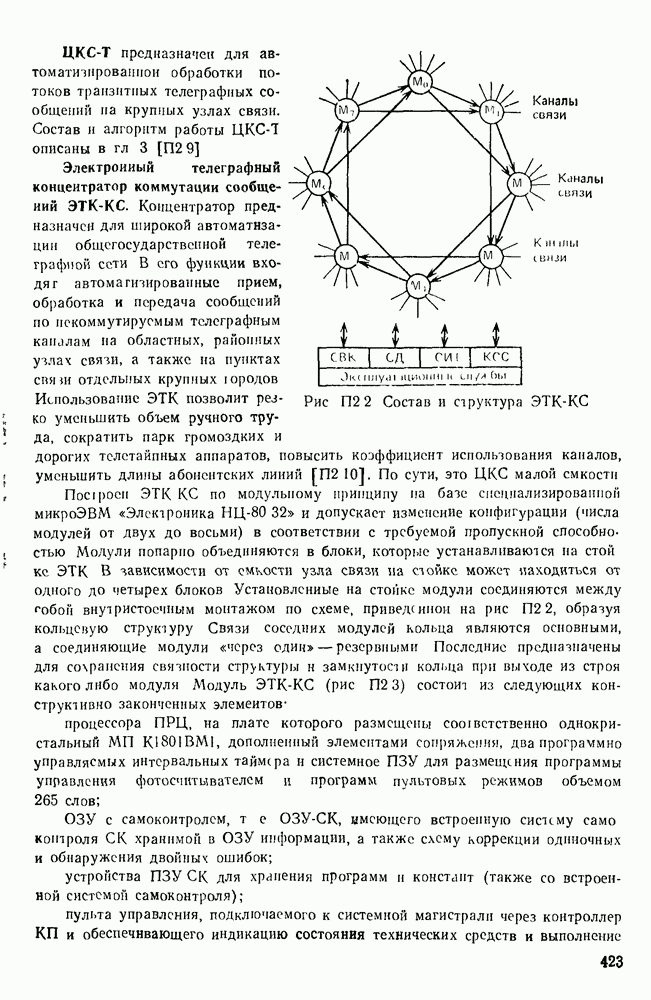
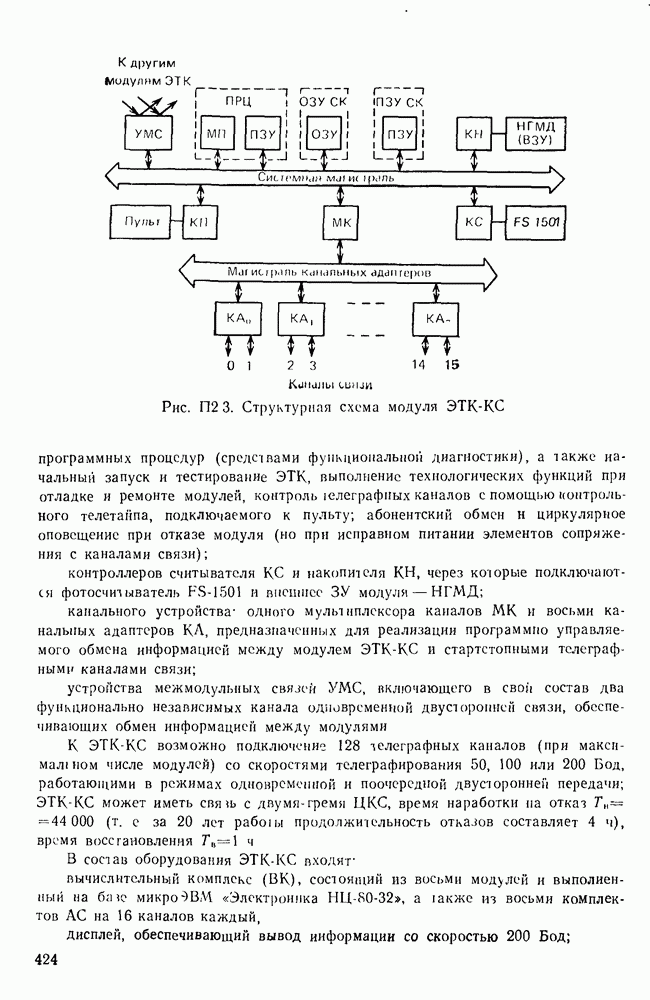
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
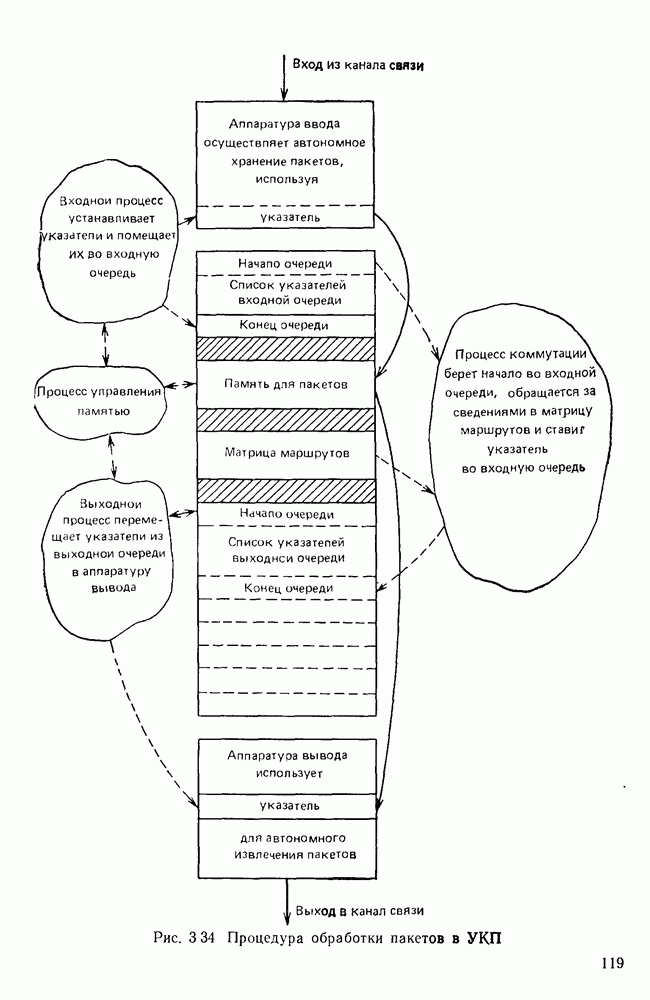
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
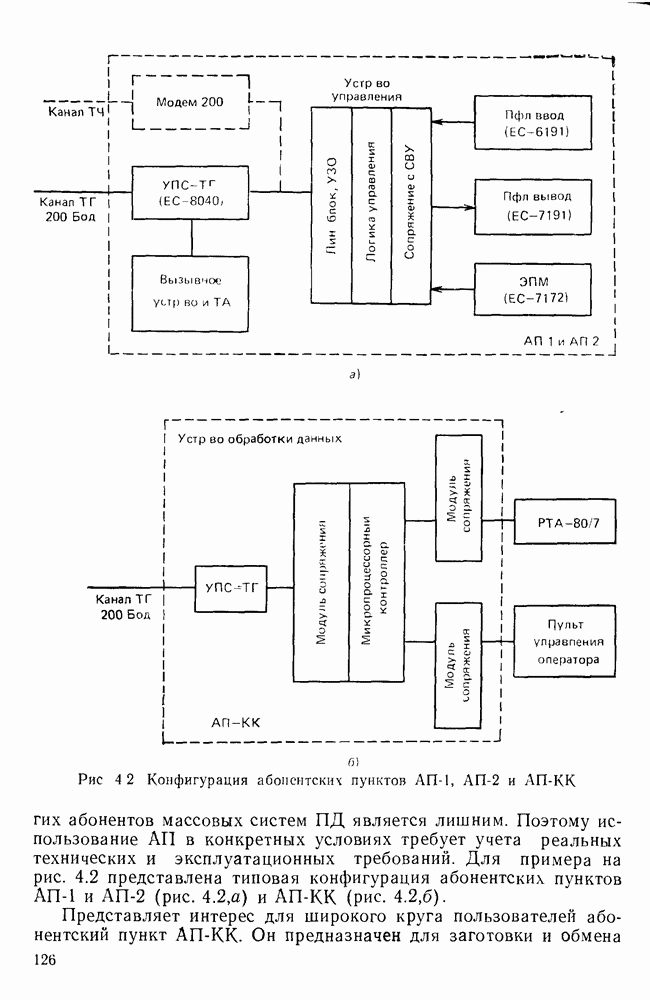
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
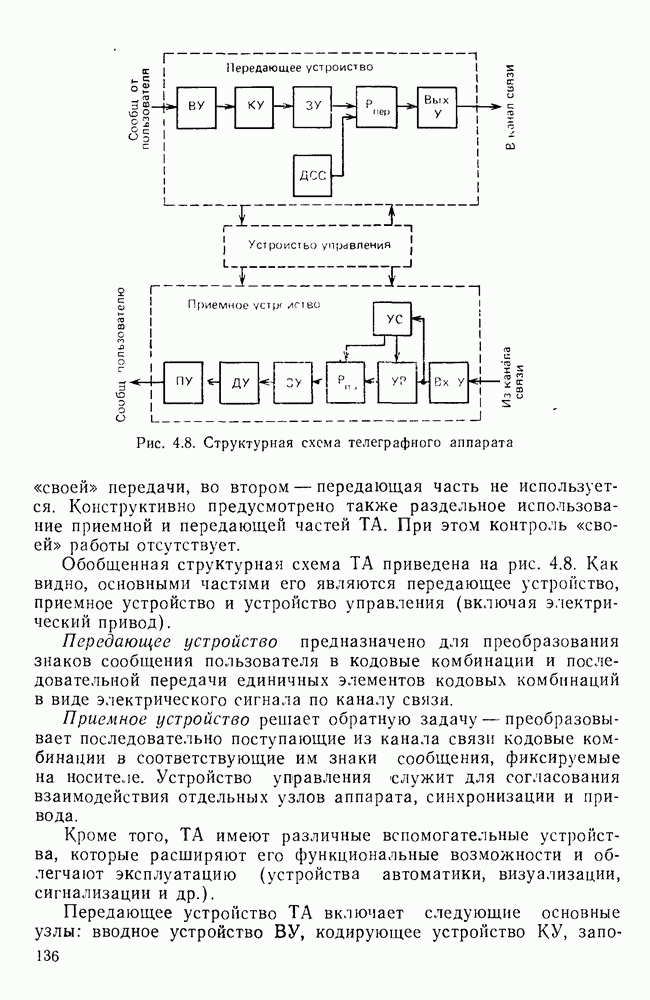
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
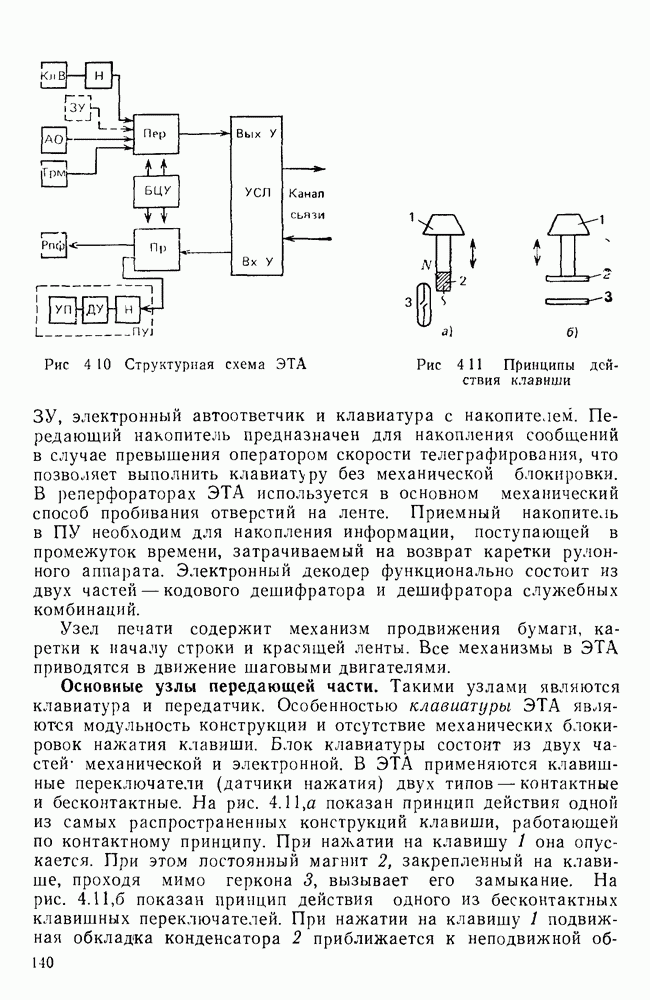
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
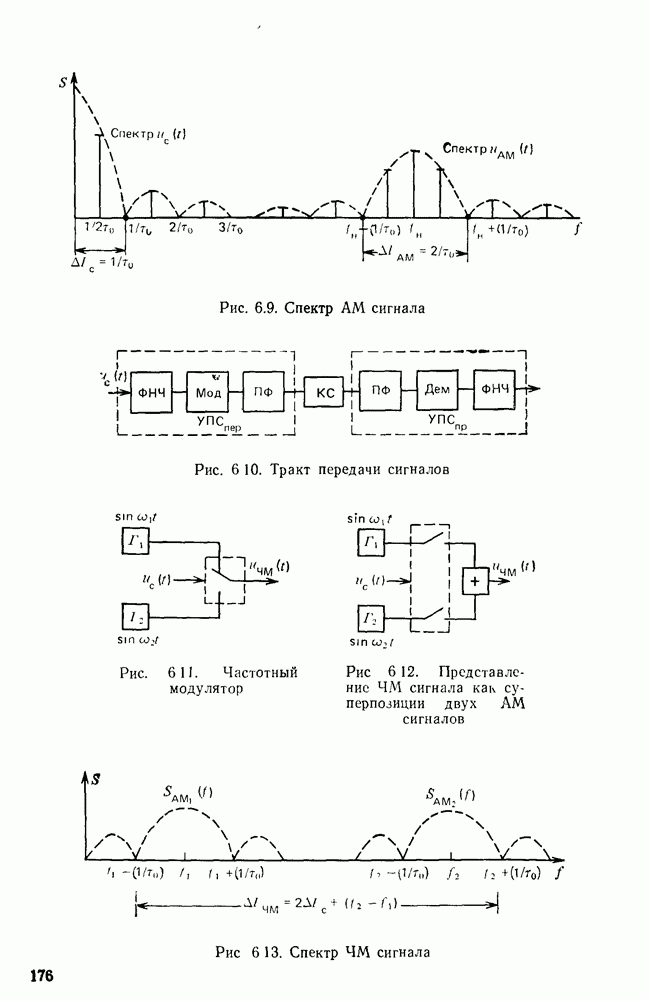
- Модулированные сигналы.
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
- Основы микропроцессорной реализации модуляторов УПС.
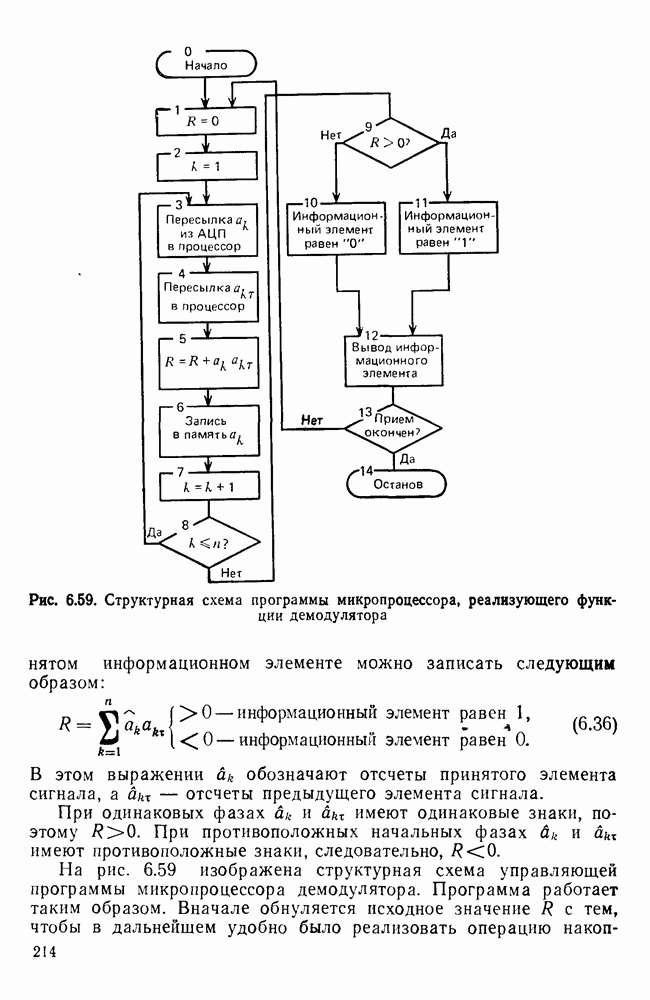
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
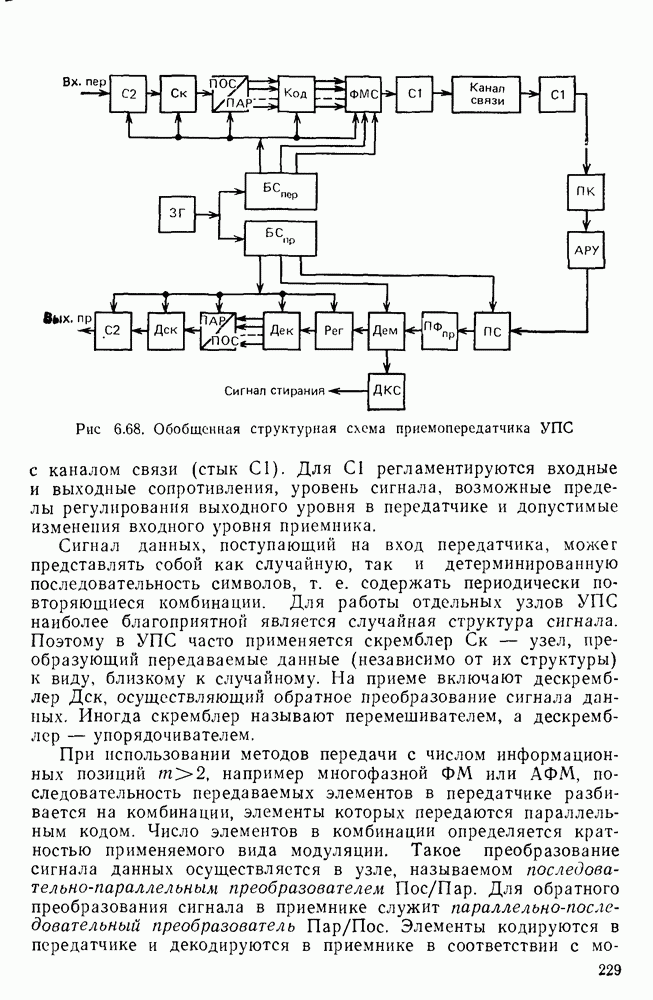
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
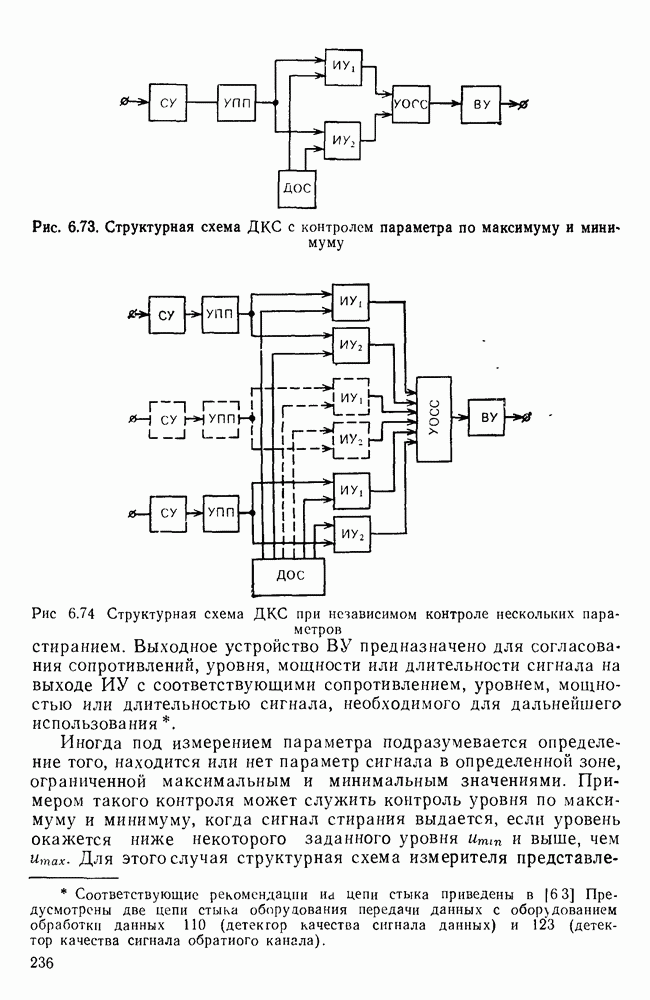
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
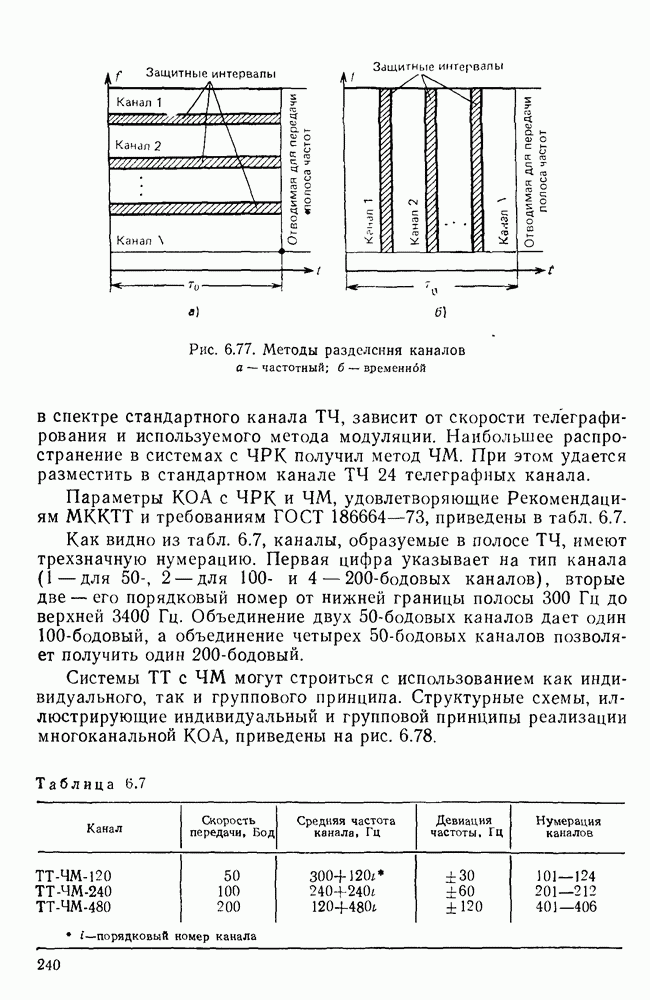
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
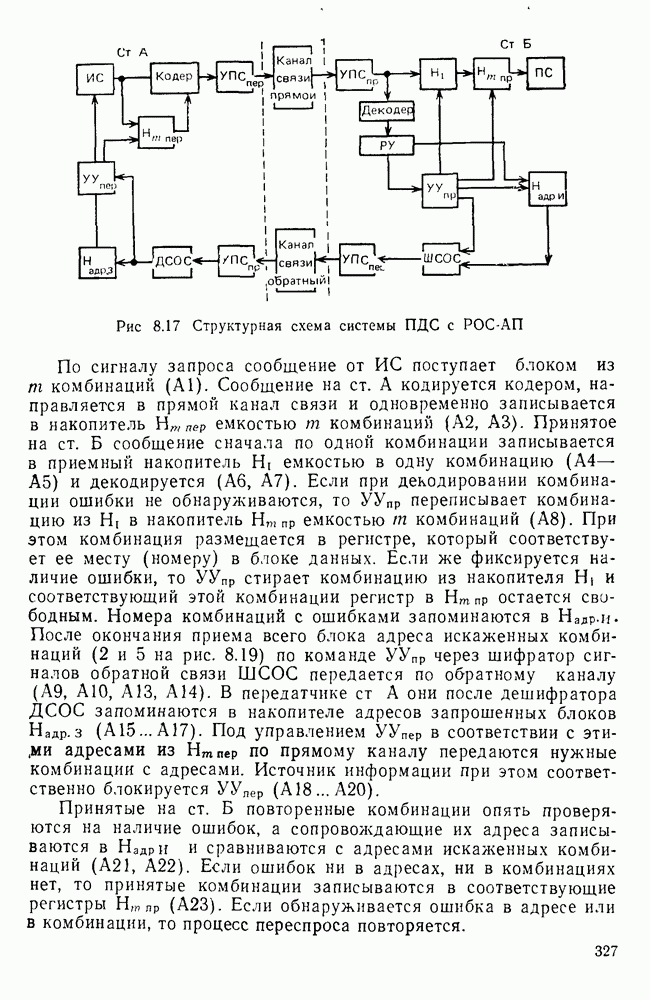
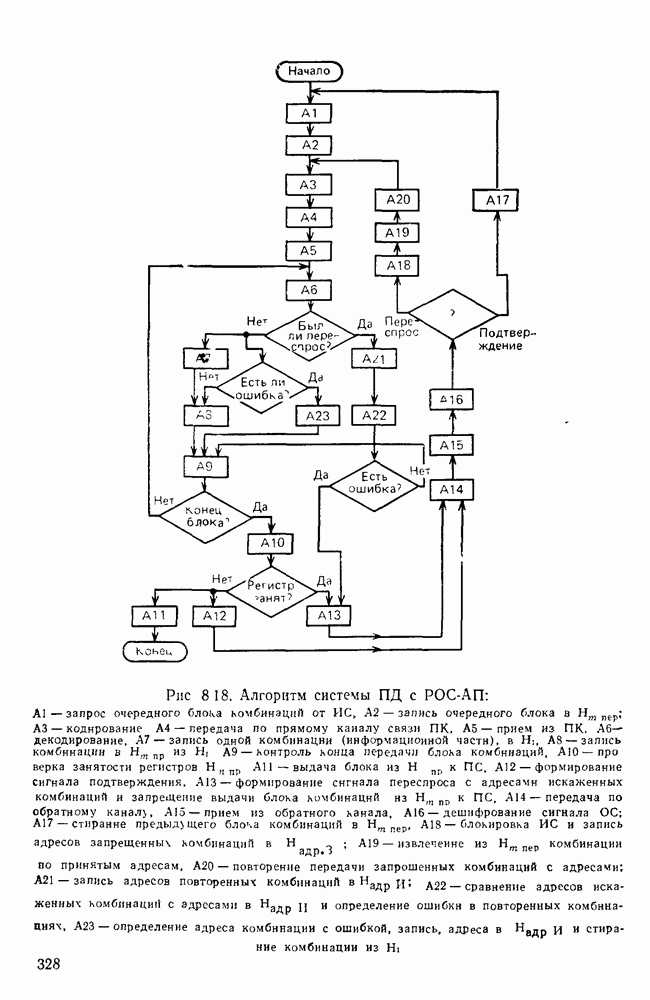
- Система с РОС и адресным переспросом РОС-АП.
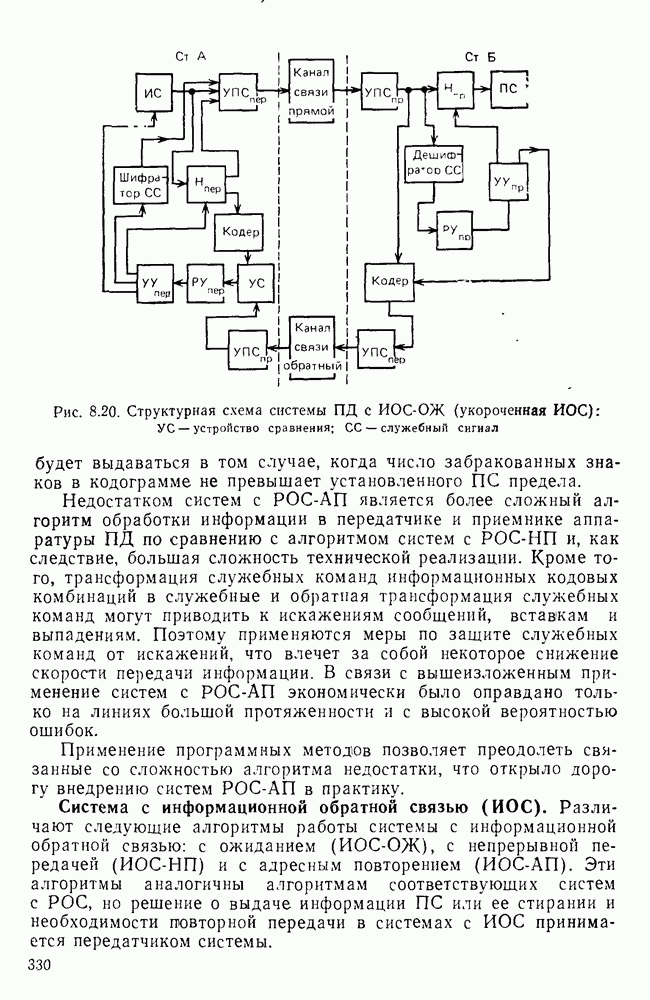
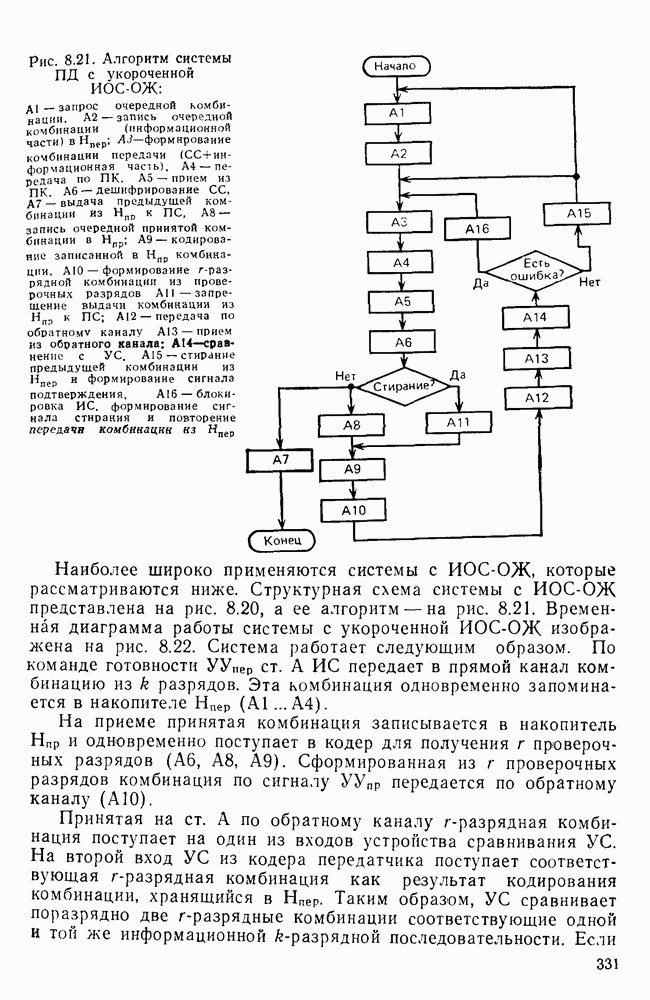
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
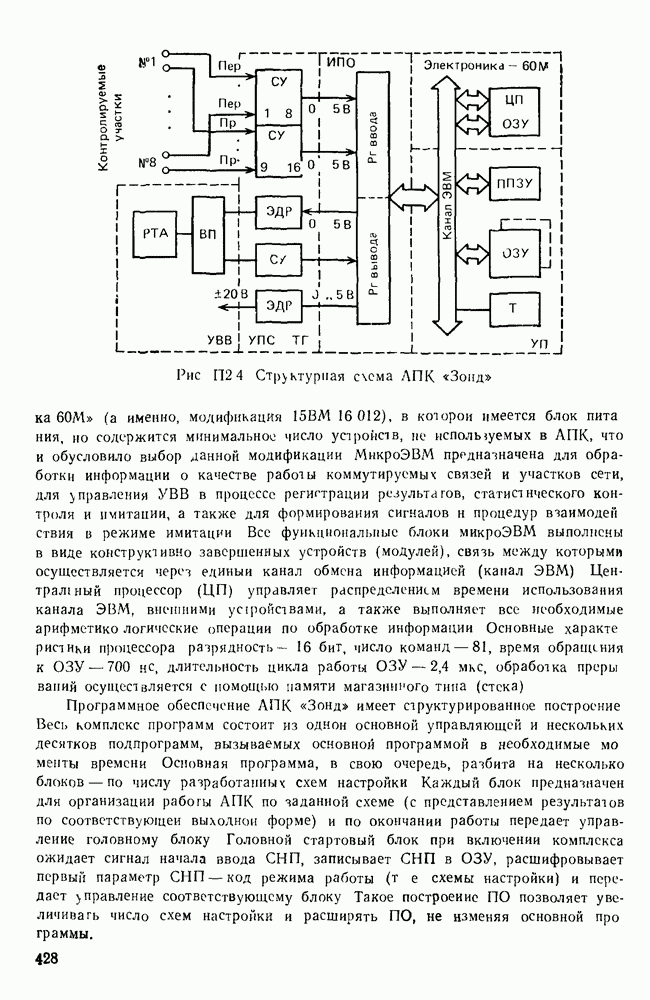
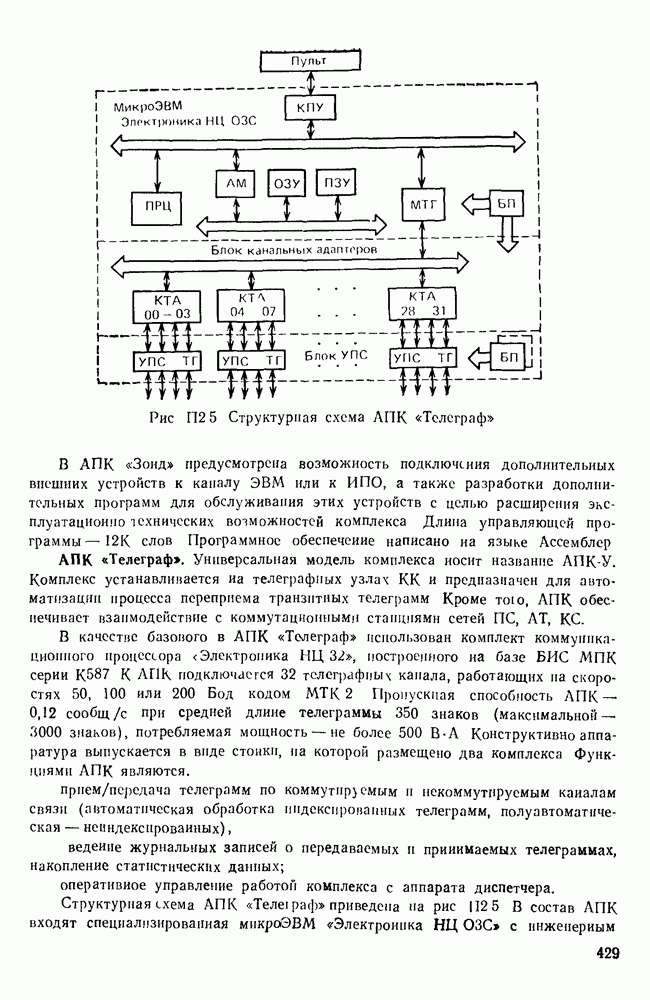
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ