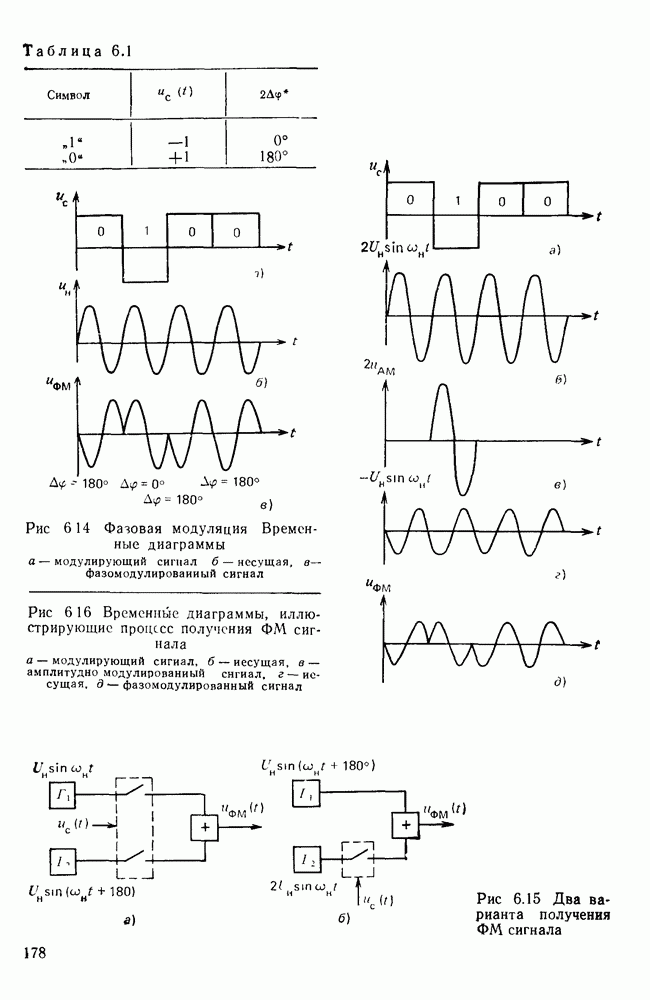
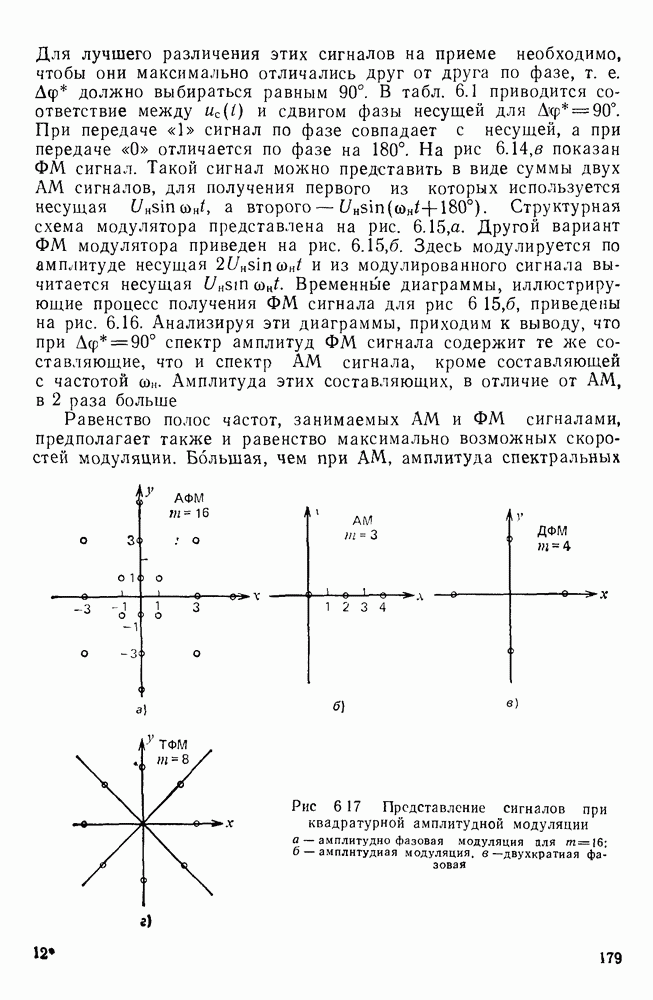
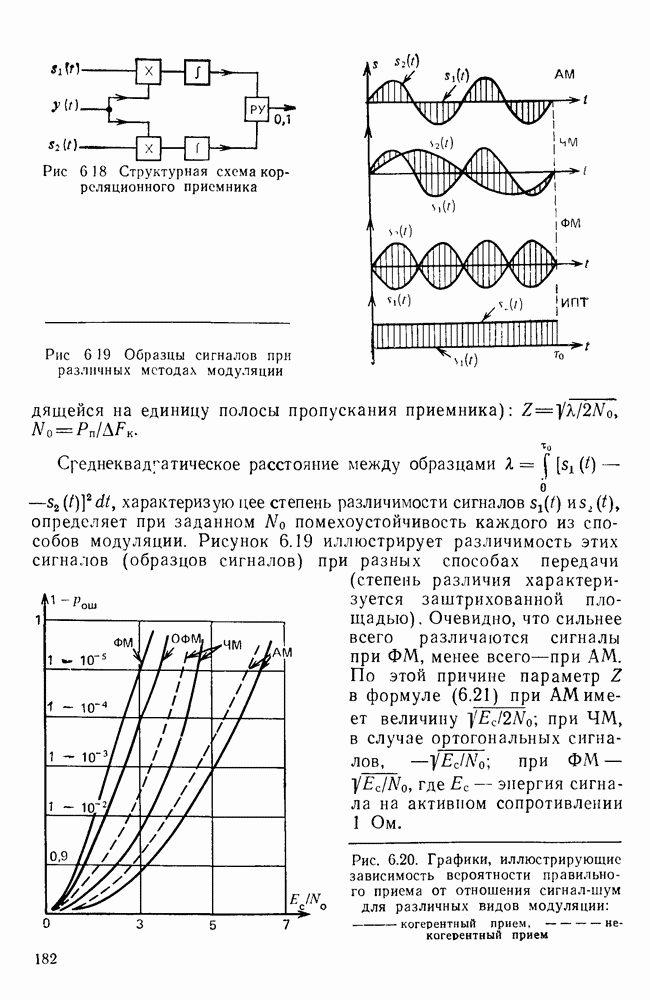
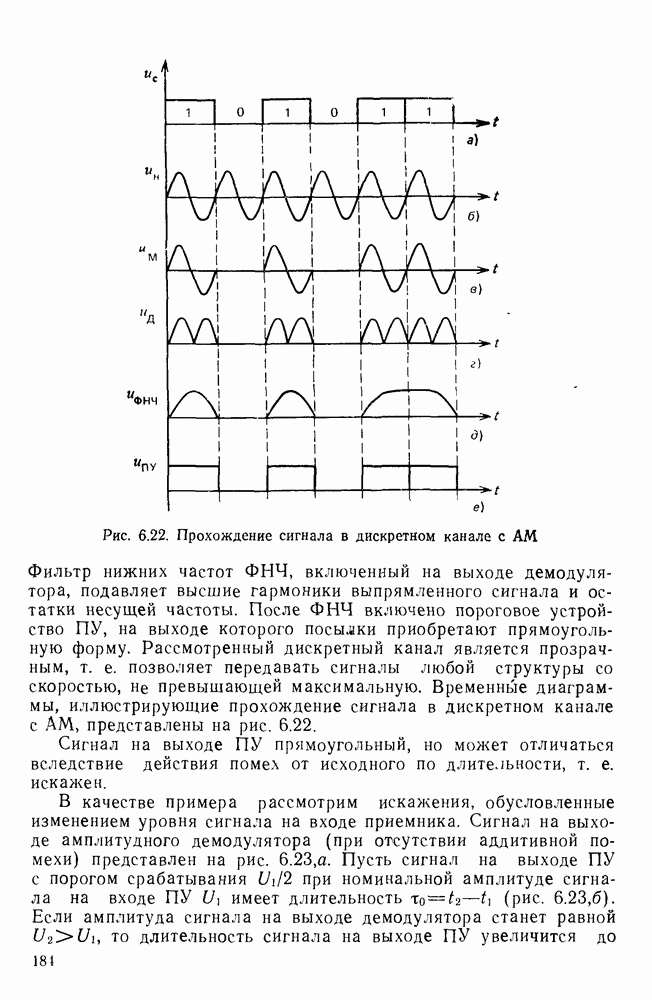
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
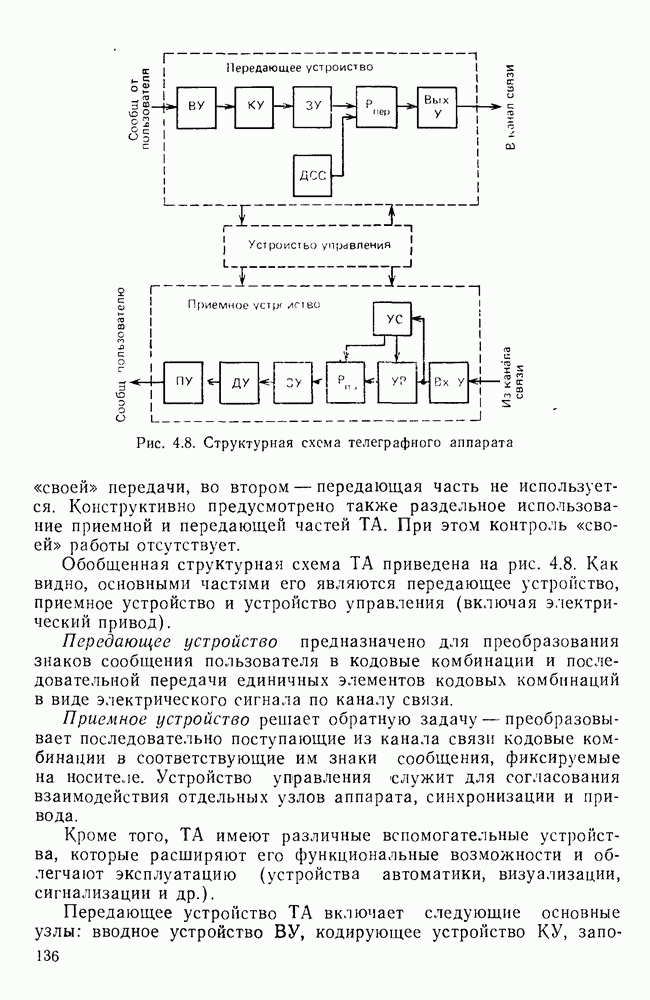
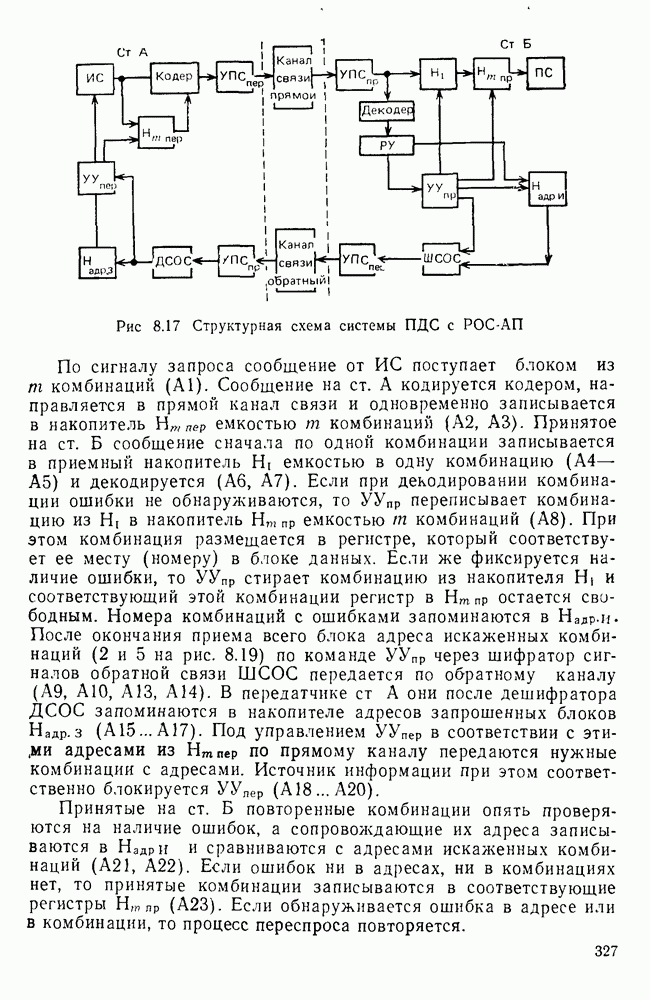
2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
Случайный процесс возникновения ошибок в дискретном канале будет полностью описан, если заданы: входной (А) и выходной (А) алфавиты символов, а также совокупность переходных вероятностей вида  , где
, где  — произвольная последовательность символов входного алфавита и
— произвольная последовательность символов входного алфавита и  — символ на входе канала в
— символ на входе канала в  момент времени
момент времени  — соответствующая а последовательность символов из выходного алфавита, а
— соответствующая а последовательность символов из выходного алфавита, а  — символ на выходе канала в
— символ на выходе канала в  момент;
момент;  - условная вероятность приема последовательности а при условии, что передана последовательность а.
- условная вероятность приема последовательности а при условии, что передана последовательность а.

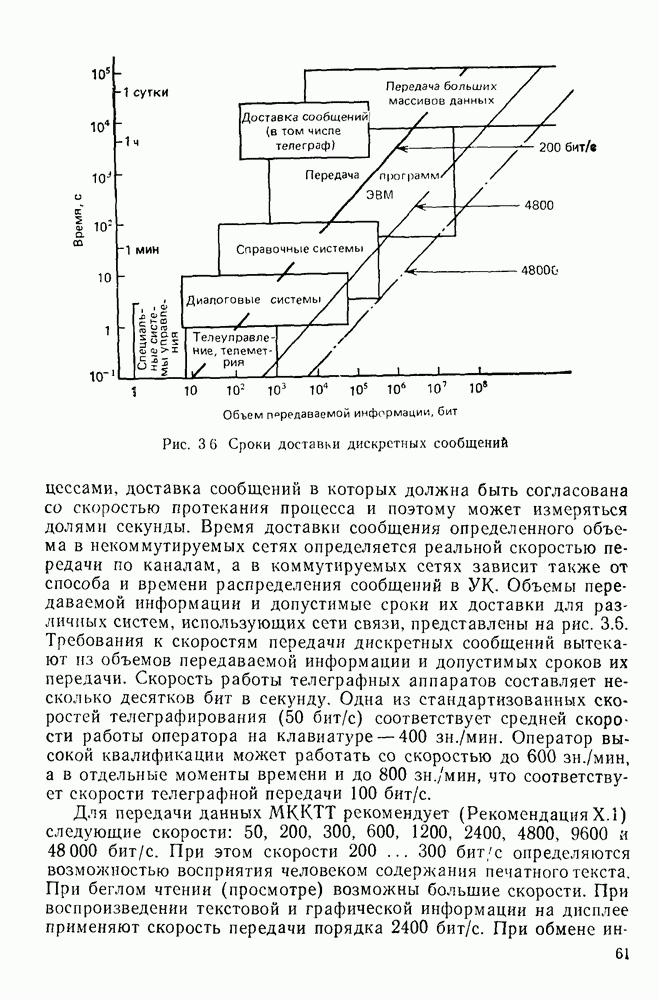
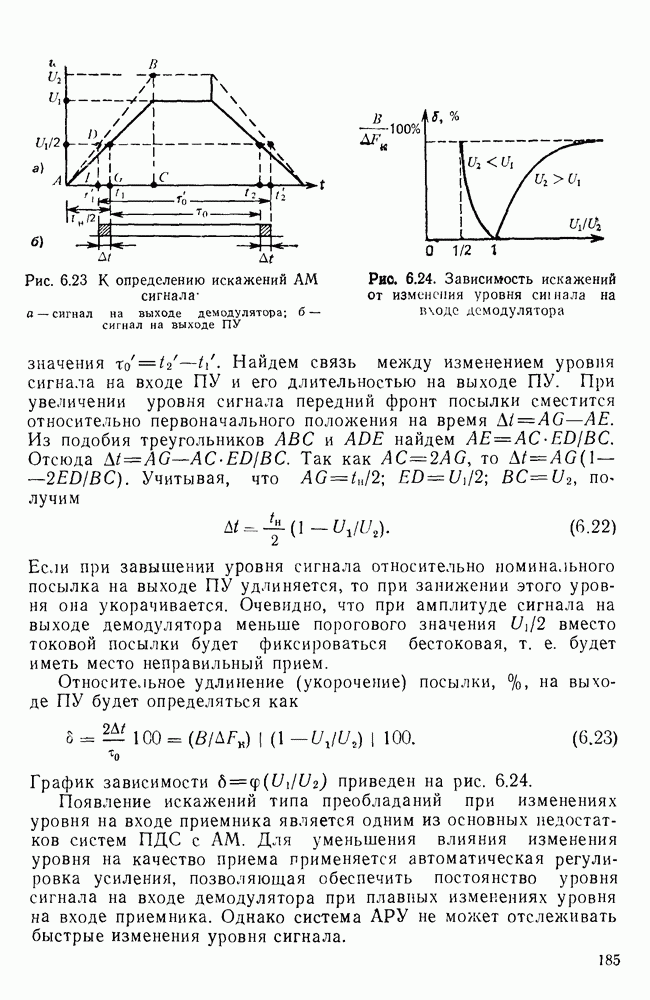
Рис. 2.13 Диаграмма переходов в двоичном канале

Рис. 2.14. Эквивалентная схема дискретного симметричного канала
Число задаваемых переходных вероятностей с увеличением длины входных и выходных последовательностей растет. Так, если используется двоичный код и выходной алфавит равен входному, то при последовательности длины  общее число задаваемых переходных вероятностей будет равно
общее число задаваемых переходных вероятностей будет равно  . Очевидно, что уже при
. Очевидно, что уже при  задание переходных вероятностей в виде таблицы хотя и возможно, но вряд ли целесообразно.
задание переходных вероятностей в виде таблицы хотя и возможно, но вряд ли целесообразно.
Рассмотрим некоторые математические модели ошибок в дискретном канале, позволяющие достаточно просто рассчитать переходные вероятности  для любых последовательностей конечной длины
для любых последовательностей конечной длины 
Дискретный канал без памяти.
Если в любой момент вероятность появления символа на выходе дискретного канала зависит только от символа на входе канала для всех пар символов на входе и выходе, то такой канал называется каналом без памяти. Примером дискретного канала без памяти может служить двоичный симметричный канал (ДСК), граф которого изображен на рис. 2.13. Каждый символ последовательности а на входе с некоторой фиксированной вероятностью q воспроизводится на выходе канала правильно  и с вероятностью
и с вероятностью  — неправильно.
— неправильно.
Для ДСК легко вычисляется вероятность получения любой последовательности символов на выходе при заданной последовательности на входе. Например, для последовательности длины 3 имеем 
Симметричный канал можно представить как канал, к которому подключен источник ошибок (рис. 2.14). Этот источник выдает случайную последовательность ошибок  . Каждая позиция
. Каждая позиция  , складывается с соответствующей позицией а, в двоичном канале по модулю
, складывается с соответствующей позицией а, в двоичном канале по модулю  Там, где в последовательности ошибок
Там, где в последовательности ошибок  стоит 1, передаваемый символ изменится на обратный, т. е. в принятой последовательности
стоит 1, передаваемый символ изменится на обратный, т. е. в принятой последовательности  будет ошибка. Например, если
будет ошибка. Например, если  , то
, то 
Переходные вероятности для стационарного симметричного канала принимают

т. е. канал полностью описывается статистикой последовательности ошибок  где
где  Последовательность ошибок длины
Последовательность ошибок длины  иногда называют вектором ошибок длины
иногда называют вектором ошибок длины  . Этот вектор имеет единицы только на позициях, соответствующих неправильно принятым символам. Число единиц
. Этот вектор имеет единицы только на позициях, соответствующих неправильно принятым символам. Число единиц  в векторе ошибок называют его весом.
в векторе ошибок называют его весом.
На практике при приеме последовательности длины  нас часто интересуют вероятности отсутствия и наличия в ней одной, двух и т. д. ошибок. Для ДСК эти вероятности легко вычисляются. Обозначим
нас часто интересуют вероятности отсутствия и наличия в ней одной, двух и т. д. ошибок. Для ДСК эти вероятности легко вычисляются. Обозначим  вероятность того, что среди
вероятность того, что среди  принятых символов имеется t ошибок в любом сочетании, а через
принятых символов имеется t ошибок в любом сочетании, а через  — вероятность одного заданного сочетания ошибок веса I. Тогда
— вероятность одного заданного сочетания ошибок веса I. Тогда  найдется как сумма
найдется как сумма  для всех возможных последовательностей ошибок веса t. Следовательно,
для всех возможных последовательностей ошибок веса t. Следовательно,

где 
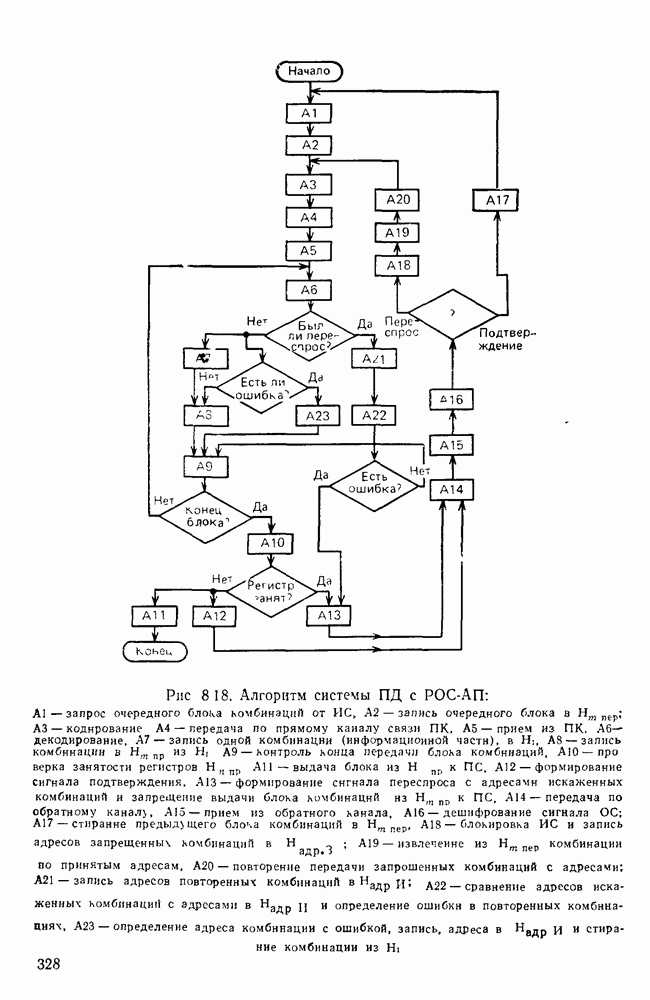
Каналы с памятью.
Канал, в котором каждый символ выходной последовательности зависит как от соответствующего символа на входе, так и от прошлых входных и выходных символов, называется каналом с памятью. Большинство реальных каналов является каналами с памятью. Одной из причин появления памяти является межсимвольная интерференция, возникающая из-за ограничения полосы пропускания канала связи. В этом случае каждый символ на выходе канала частично зависит от нескольких следующих друг за другом символов на входе (зависимость эта определяется импульсной характеристикой канала). Другой причиной могут быть перерывы в канале, длительность которых значительно превышает длительность единичного элемента. В период действия перерыва вероятность неправильного приема резко возрастает и появляется последовательность ошибок, называемая пакетом.
В общем случае для канала с памятью можно ввести понятие «состояние канала». Тогда каждый символ последовательности на выходе канала будет статистически зависеть как от соответствующего символа на входе, так и от состояния канала в данный момент. Под состоянием канала в заданный момент можно понимать, например, вид последовательности входных и выходных символов вплоть до заданного момента. Так, отражается, в частности, влияние межсимвольной интерференции.
Различают каналы с памятью по входу и каналы с памятью по выходу. Если выходной символ статистически зависит от входных символов  , то такой канал называется каналом с памятью по входу. Такой канал характеризуется переходными вероятностями вида
, то такой канал называется каналом с памятью по входу. Такой канал характеризуется переходными вероятностями вида  . Теоретически память канала бесконечна. Практически число символов, влияющих на вероятности правильного и ошибочного приема символа, ограничено. Память канала может быть определена как число символов N, начиная с которого справедливо равенство условных вероятностей
. Теоретически память канала бесконечна. Практически число символов, влияющих на вероятности правильного и ошибочного приема символа, ограничено. Память канала может быть определена как число символов N, начиная с которого справедливо равенство условных вероятностей

Последовательность входных символов  можно представить как состояние канала
можно представить как состояние канала  момент. Тогда канал будет характеризоваться совокупностью переходных вероятностей вида
момент. Тогда канал будет характеризоваться совокупностью переходных вероятностей вида 
Если выходной символ а, статистически зависит от нескольких предыдущих выходных символов, то такой канал называется каналом с памятью по выходу. Переходные вероятности для такого канала записываются в виде

где выходные символы  можно представить как состояние канала
можно представить как состояние канала  момент.
момент.
Задание канала с памятью с использованием переходных вероятностей вида (2.8) или (2.9) было бы чрезвычайно громоздким. Так, если для канала с межсимвольной интерференцией память по входу ограничивается пятью символами, то число состояний канала будет равно 32. В общем случае, если память только по входу или только по выходу ограничивается в двоичном канале N символами, то число состояний равно  Как видно, число состояний растет по экспоненциальному закону в зависимости от длины памяти N. Следует заметить, что некоторые реальные каналы имеют память в десятки, сотни и даже тысячи символов!
Как видно, число состояний растет по экспоненциальному закону в зависимости от длины памяти N. Следует заметить, что некоторые реальные каналы имеют память в десятки, сотни и даже тысячи символов!
Состояния каналов можно различать по вероятности ошибки в каждом из состояний. Изменения вероятности ошибки можно в свою очередь связать с физическими причинами — появлением перерывов, импульсных помех, замираний и т. д. Такой канал можно задать совокупностью переходных вероятностей вида  где L — конечное множество состояний канала.
где L — конечное множество состояний канала.
Если предположить, что имеется статистическая независимость между символом а, и состоянием с, при условии, что заданы а, и предыдущее состояние  то можно записать:
то можно записать:


Рис. 2.15 Эквивалентная схема дискретного симметричного канала при описании его моделью на основе цепей Маркова

Рис. 2.16 Диаграммы переходов при описании дискретного симметричного канала моделью Гильберта: а — из одного состояния в другое; б — возможные исходы передачи в состоянии 2
В этом случае необходимо задать переходные вероятности для состояний канала  и вероятности переходов
и вероятности переходов  для символов для каждого состояния канала. Таким образом, канал имеет конечное множество состояний, переходные вероятности для которых не зависят от времени. Ошибки в каждом состоянии возникают независимо с постоянной вероятностью. Последовательность состояний является простой цепью Маркова. (Простой цепью Маркова называется случайная последовательность состояний, когда вероятность того или иного состояния в
для символов для каждого состояния канала. Таким образом, канал имеет конечное множество состояний, переходные вероятности для которых не зависят от времени. Ошибки в каждом состоянии возникают независимо с постоянной вероятностью. Последовательность состояний является простой цепью Маркова. (Простой цепью Маркова называется случайная последовательность состояний, когда вероятность того или иного состояния в  момент полностью определяется состоянием
момент полностью определяется состоянием  момент). Эквивалентная схема такого канала представлена на рис. 2.15.
момент). Эквивалентная схема такого канала представлена на рис. 2.15.
Для описания простой цепи Маркова необходимо задать переходные вероятности  того, что система в
того, что система в  момент перейдет в состояние с, при условии, что в
момент перейдет в состояние с, при условии, что в  момент она находилась в состоянии
момент она находилась в состоянии  и вероятности ошибок в каждом из возможных состояний
и вероятности ошибок в каждом из возможных состояний  . В рассмотренной модели канала с памятью состояния канала статистически не зависят от входных и выходных символов. Достоинством такой модели является то, что достаточно большую память канала можно описать относительно малым числом состояний. Увеличивая число состояний, можно более точно описать реальный канал. Однако сложность использования модели в расчетах будет существенно возрастать с увеличением числа состояний.
. В рассмотренной модели канала с памятью состояния канала статистически не зависят от входных и выходных символов. Достоинством такой модели является то, что достаточно большую память канала можно описать относительно малым числом состояний. Увеличивая число состояний, можно более точно описать реальный канал. Однако сложность использования модели в расчетах будет существенно возрастать с увеличением числа состояний.
Простейшей моделью, основанной на применении математического аппарата марковских цепей является модель источника ошибок, предложенная Гильбертом. Согласно этой модели канал может находиться в двух состояниях — хорошем (состояние 1) и плохом (состояние 2).
Первое состояние характеризуется отсутствием ошибок. Во втором состоянии ошибки появляются с вероятностью 
Если при передаче элемента а, канал находится в состоянии 1, то при передаче следующего элемента  канал будет находиться в том же состоянии с вероятностью
канал будет находиться в том же состоянии с вероятностью  и в состоянии 2 — с вероятностью
и в состоянии 2 — с вероятностью  . Если же при передаче элемента а, канал находился в состоянии 2, то при передаче элемента
. Если же при передаче элемента а, канал находился в состоянии 2, то при передаче элемента  он может находиться в том же состоянии с вероятностью
он может находиться в том же состоянии с вероятностью  и в состоянии 1 — с вероятностью
и в состоянии 1 — с вероятностью  Матрицу переходов из состояния в состояние обозначим Р:
Матрицу переходов из состояния в состояние обозначим Р:

Если  достаточно велики, но не равны между собой, то наблюдается тенденция к сохранению возникшего состояния 1 или 2, что имитирует канал с пакетами ошибок.
достаточно велики, но не равны между собой, то наблюдается тенденция к сохранению возникшего состояния 1 или 2, что имитирует канал с пакетами ошибок.
На графе (рис. 2.16, а) состояния канала изображены в виде кружков. Направленные стрелки обозначают переходы из одного состояния в другое, число на каждой стрелке указывает вероятность перехода. Для канала, взятого в качестве примера, в состоянии 2 возникают ошибки с вероятностью 0,4 (рис. 2.16,б).
Канал, представленный графом на рис. 2.16, а, имеет тенденцию пребывать в том состоянии, в котором он находится. Большую часть времени канал находится в хорошем состоянии (состояние 1), когда  . С вероятностью 10-5 канал переходит в плохое состояние, когда около 0,4 элементов на выходе канала будут ошибочными. Состояние 1 длится в среднем в течение приема 105 элементов, а состояние 2— десяти элементов. Вероятность того, что канал в момент передачи данного элемента будет находиться в том или ином состоянии, зависит от состояния, в котором канал находился при передаче предыдущего элемента. Например, вероятность того, что канал будет находиться в момент приема данного элемента в хорошем состоянии, равна
. С вероятностью 10-5 канал переходит в плохое состояние, когда около 0,4 элементов на выходе канала будут ошибочными. Состояние 1 длится в среднем в течение приема 105 элементов, а состояние 2— десяти элементов. Вероятность того, что канал в момент передачи данного элемента будет находиться в том или ином состоянии, зависит от состояния, в котором канал находился при передаче предыдущего элемента. Например, вероятность того, что канал будет находиться в момент приема данного элемента в хорошем состоянии, равна  если он в момент приема предыдущего элемента находился в хорошем состоянии, и
если он в момент приема предыдущего элемента находился в хорошем состоянии, и  если он находился в плохом состоянии.
если он находился в плохом состоянии.
Вероятность появления того или иного состояния определяется из системы уравнений:

где  — соответственно вероятности того, что канал находится в состоянии 1 или 2. Отсюда
— соответственно вероятности того, что канал находится в состоянии 1 или 2. Отсюда  Средняя вероятность ошибки в канале, описываемом моделью Гильберта, определяется выражением
Средняя вероятность ошибки в канале, описываемом моделью Гильберта, определяется выражением

Среднее число элементов на интервале времени, соответствующем плохому состоянию канала (средняя длина пакета ошибок), определяется по формуле

где  — вероятность того, что возникшее плохое состояние канала будет распространяться на i переданных элементов. Аналогично можно определить и среднюю длину интервала между ошибками:
— вероятность того, что возникшее плохое состояние канала будет распространяться на i переданных элементов. Аналогично можно определить и среднюю длину интервала между ошибками:

где  — вероятность того, что хорошее состояние канала будет длиться в течение времени передачи i элементов.
— вероятность того, что хорошее состояние канала будет длиться в течение времени передачи i элементов.
Для выбора кодов необходимо знать вероятность появления t ошибок в кодовой комбинации длиной  элементов, которая может быть найдена по формуле
элементов, которая может быть найдена по формуле

где  — вероятность того, что число элементов в кодовой комбинации, переданных за время плохого состояния канала, равно
— вероятность того, что число элементов в кодовой комбинации, переданных за время плохого состояния канала, равно  — вероятность появления
— вероятность появления  ошибок в кодовой комбинации при условии, что число элементов кодовой комбинации, переданных за время плохого состояния канала, равно
ошибок в кодовой комбинации при условии, что число элементов кодовой комбинации, переданных за время плохого состояния канала, равно  .
.
Полагая, что в кодовой комбинации длиной  элементов возможно появление только одного пакета ошибок, получим
элементов возможно появление только одного пакета ошибок, получим

Рассмотренная модель описывается тремя параметрами:  которые могут быть найдены экспериментально.
которые могут быть найдены экспериментально.
Еще более простая модель источника ошибок, для описания которой достаточно двух параметров  и
и  , где а — коэффициент группирования ошибок, предложена в [1.4]. Исследуя статистику ошибок в каналах связи, авторы обратили внимание на то, что график функции
, где а — коэффициент группирования ошибок, предложена в [1.4]. Исследуя статистику ошибок в каналах связи, авторы обратили внимание на то, что график функции  в логарифмическом масштабе по обеим осям представляется в виде прямой линии.
в логарифмическом масштабе по обеим осям представляется в виде прямой линии.
Исходя из этого можно записать

Для канала без памяти  при
при  все ошибки сосредоточены в виде одного пакета.
все ошибки сосредоточены в виде одного пакета.
Вероятность появления в комбинации ошибок кратности  и более может быть приближенно определена по формуле
и более может быть приближенно определена по формуле

Описанные выше модели дискретного канала используются для вычисления характеристик систем ПДС. Поэтому при выборе той или иной модели следует прежде всего исходить из требуемой точности расчетов. Разумеется, если имеется несколько моделей, обеспечивающих приемлемую точность, следует выбирать ту из них, которая позволит уменьшить время, требуемое для вычислений, т. е. наиболее простую.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
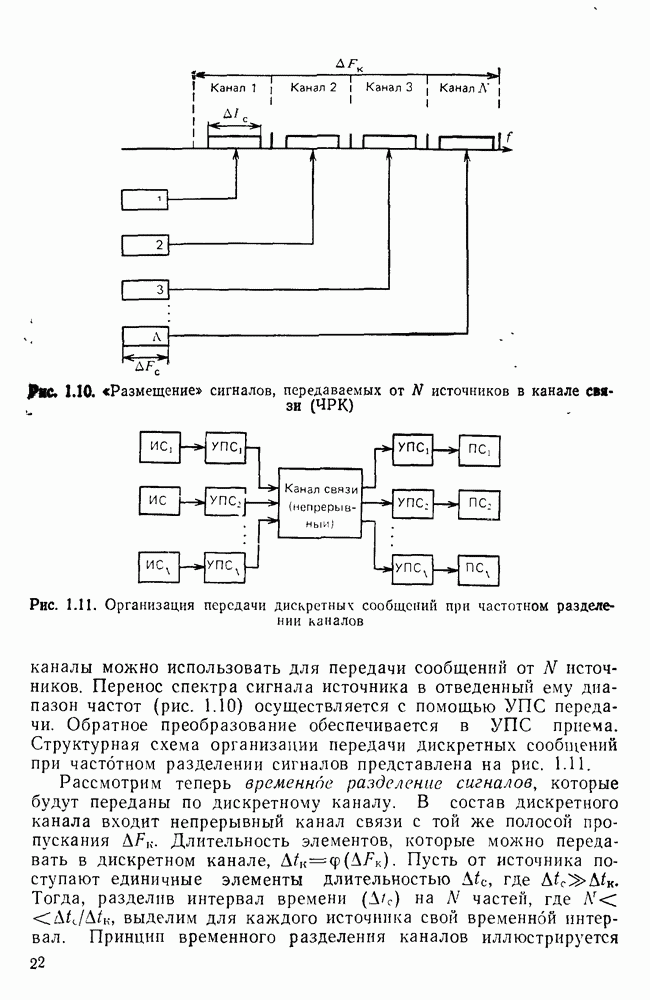
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
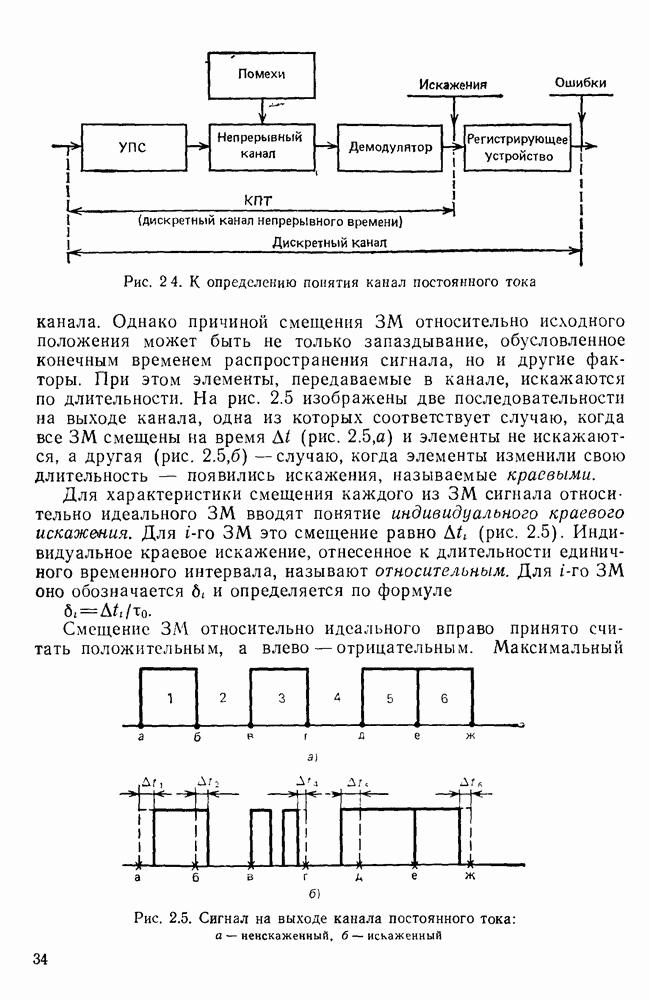
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
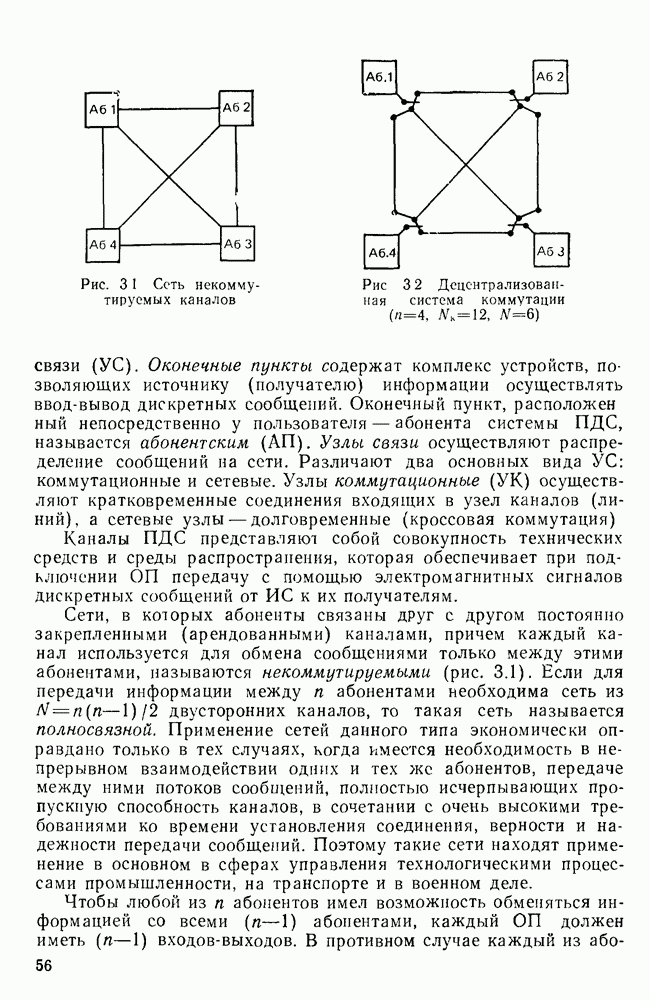
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
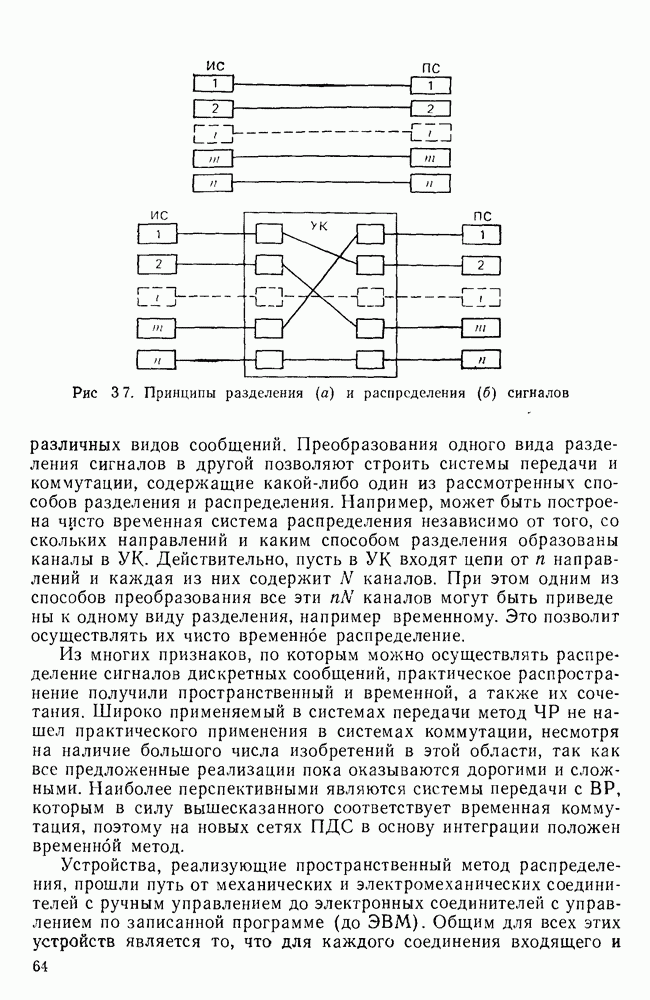
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
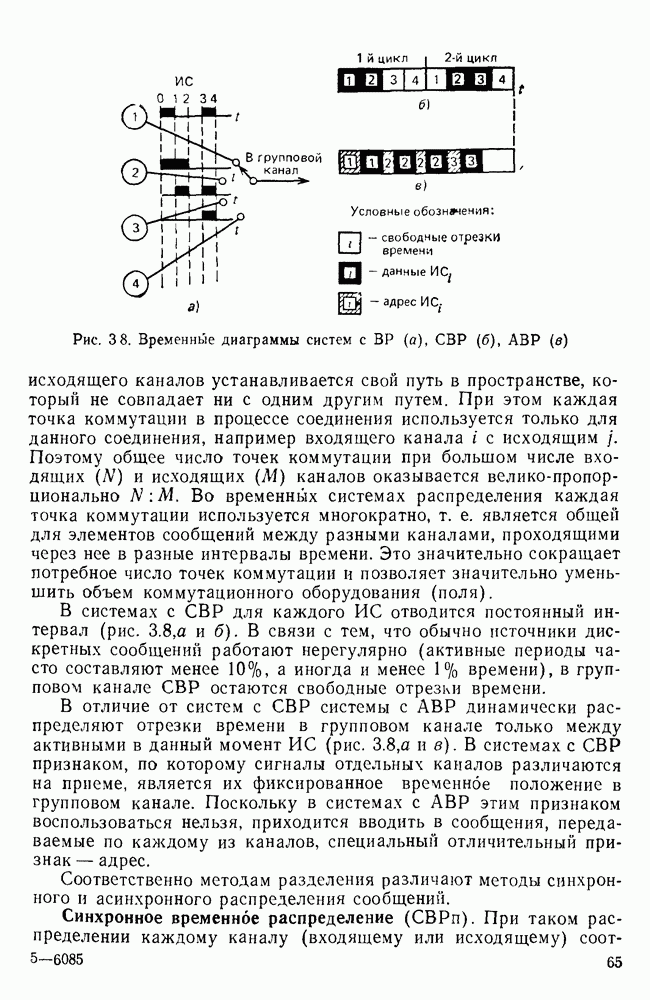
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
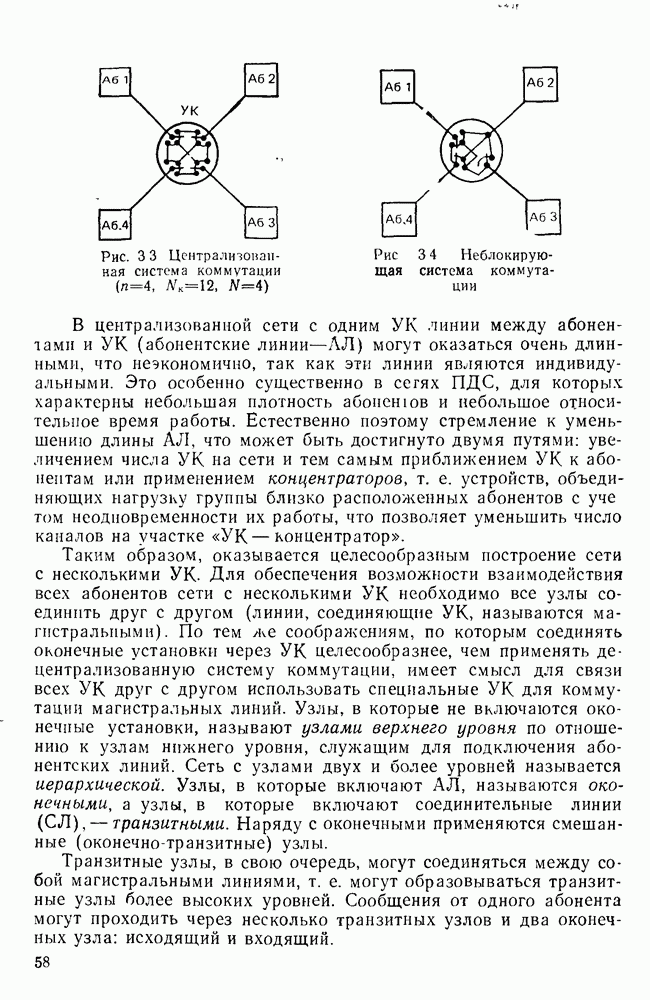
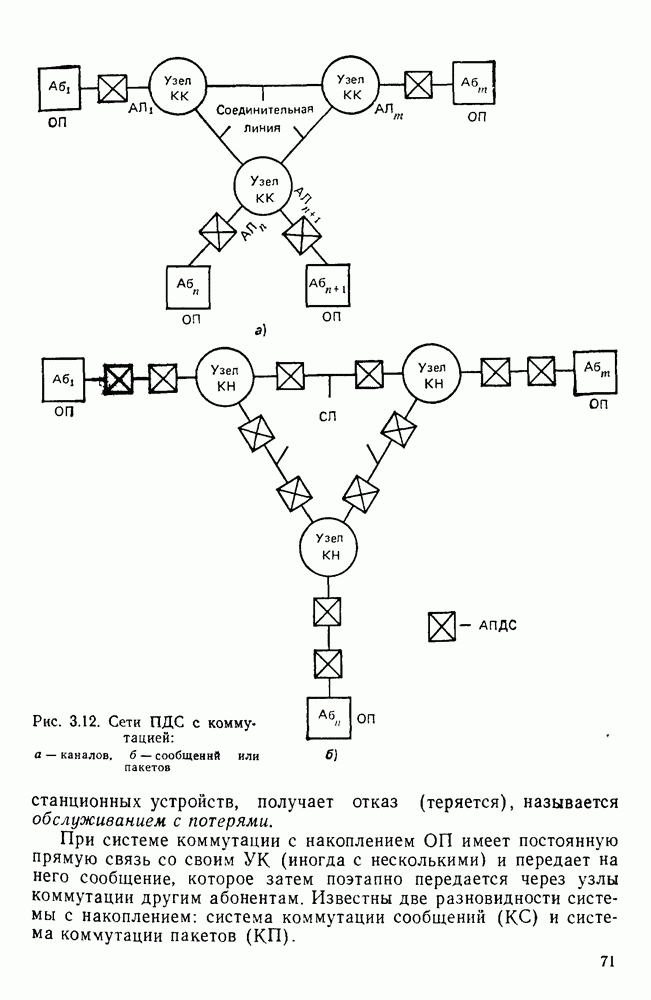
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
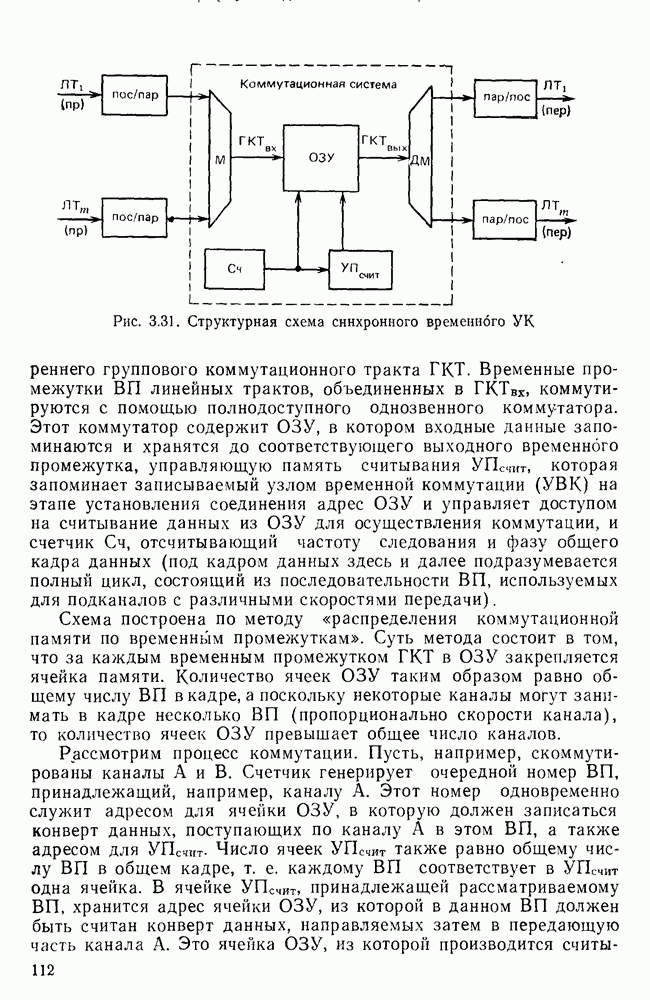
- Перспективные УК для синхронной сети.
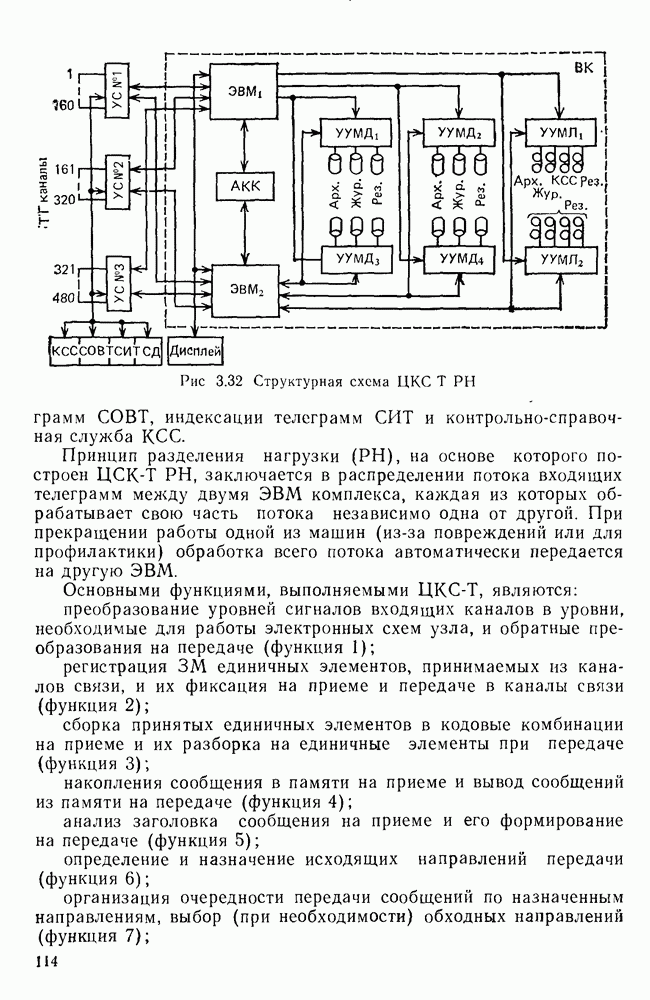
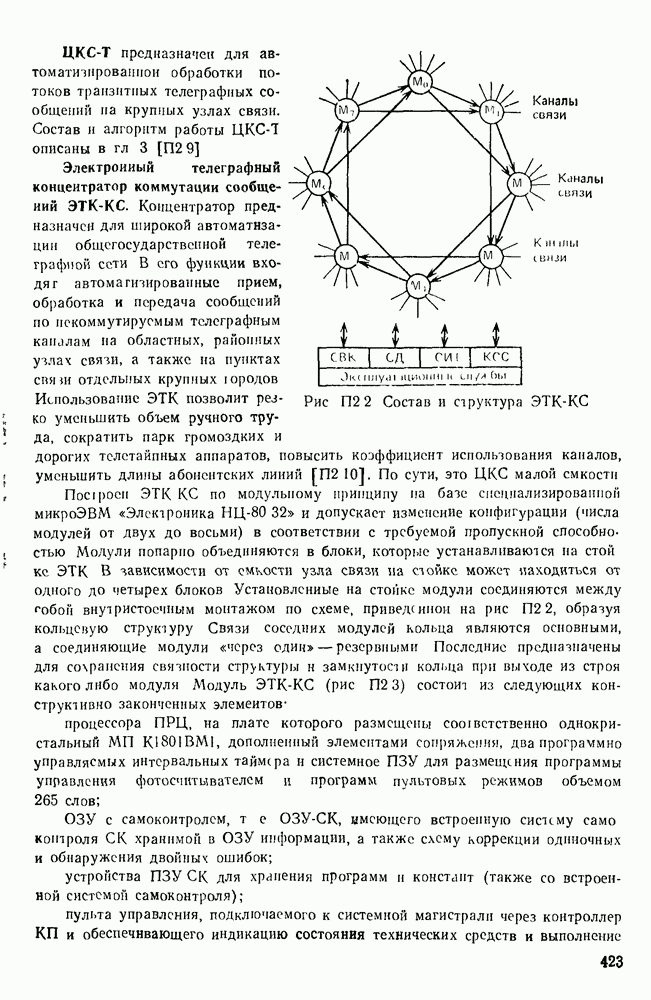
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
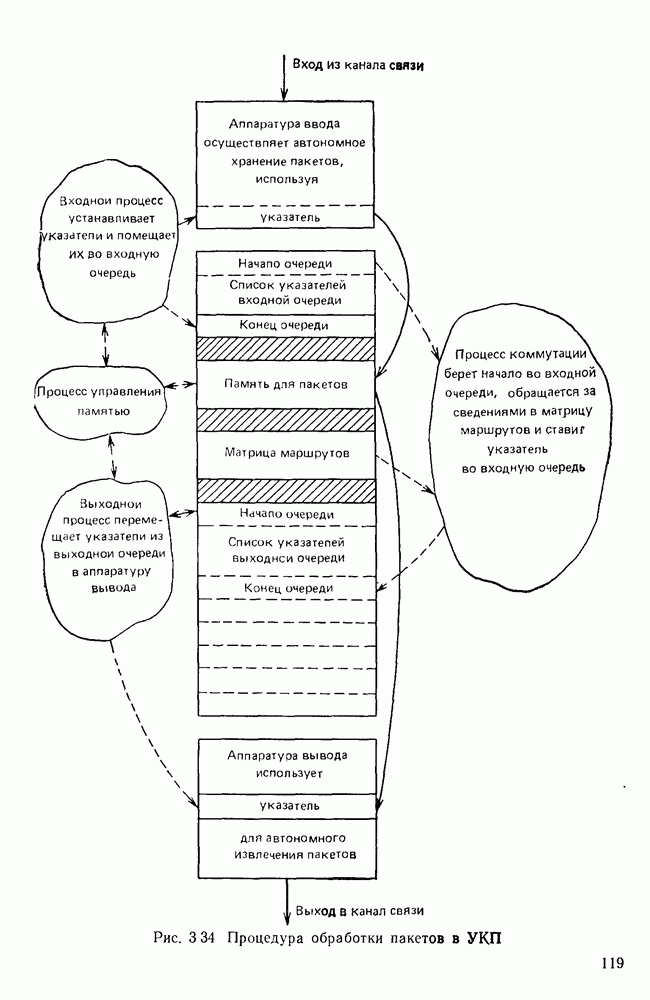
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
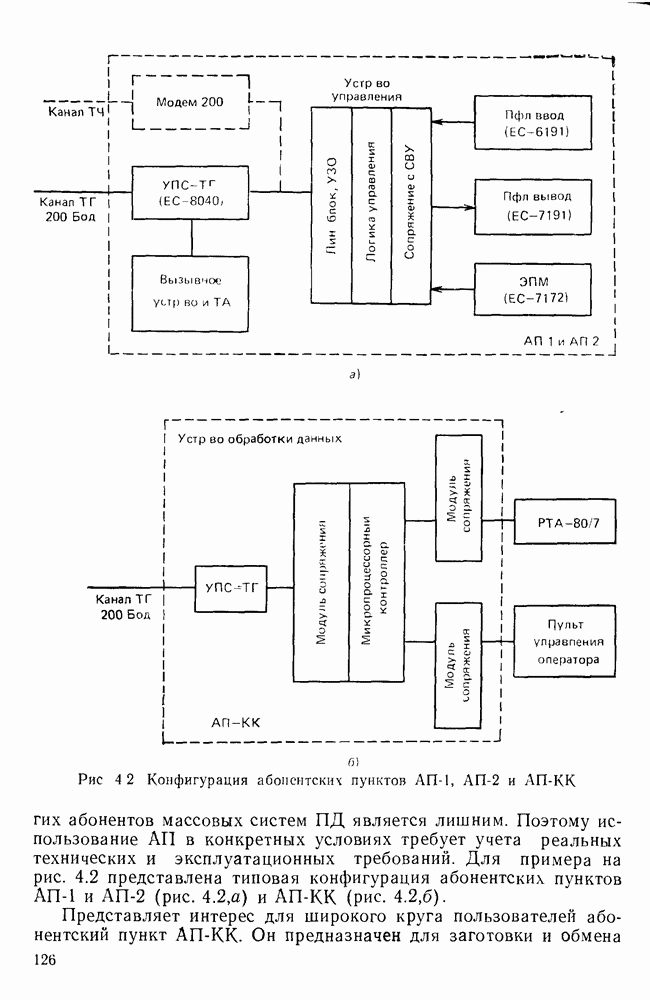
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
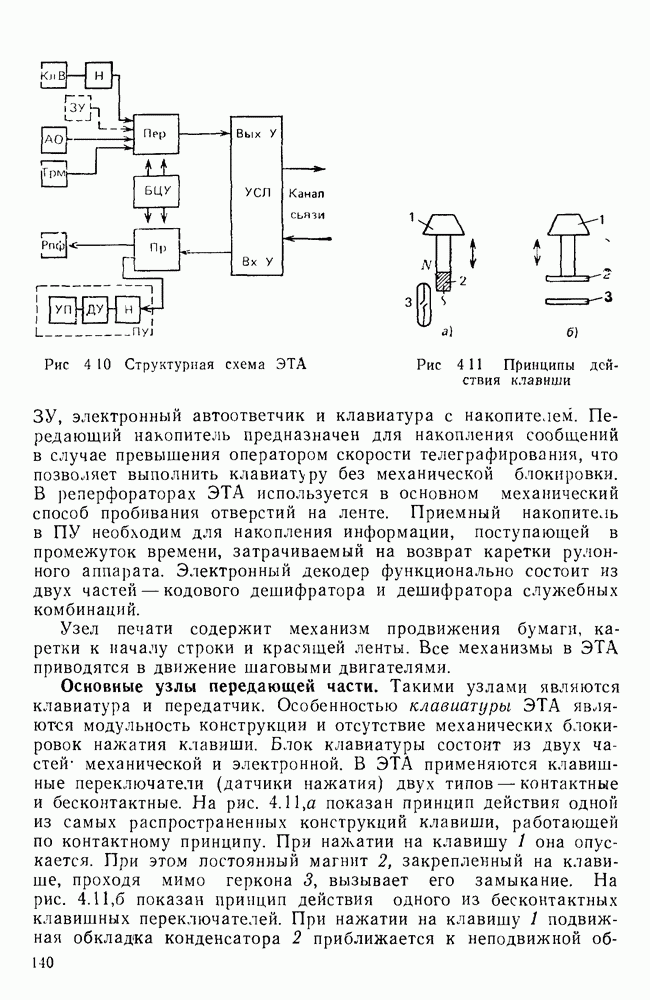
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
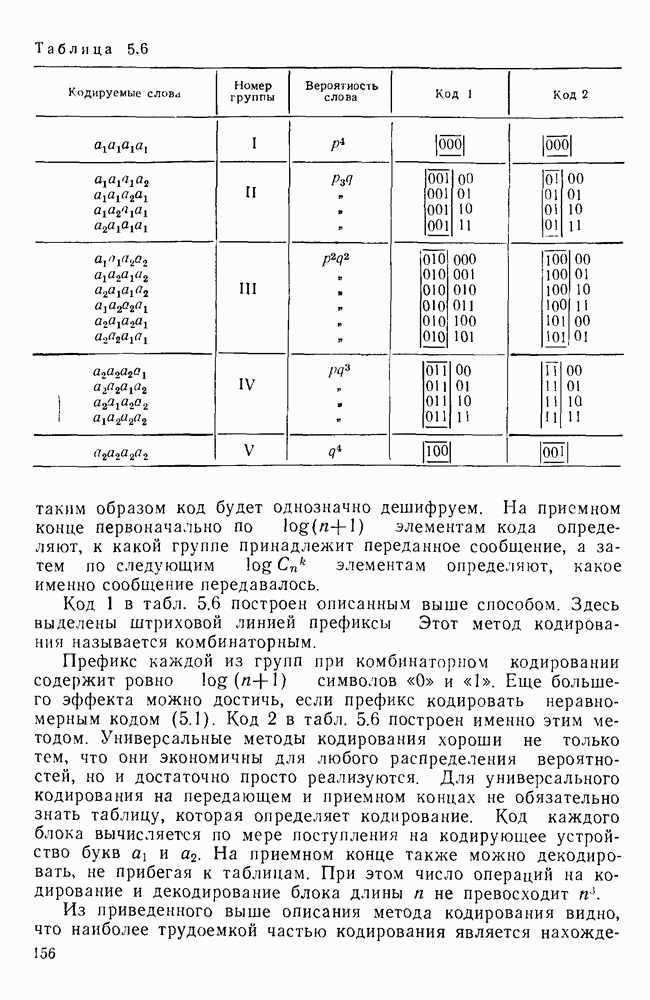
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
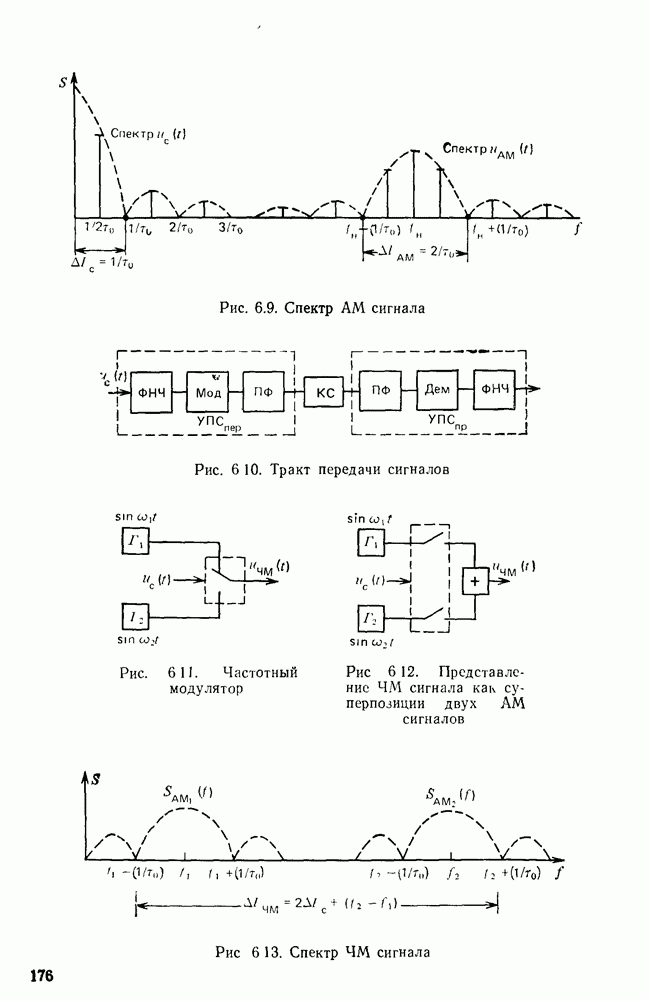
- Модулированные сигналы.
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
- Основы микропроцессорной реализации модуляторов УПС.
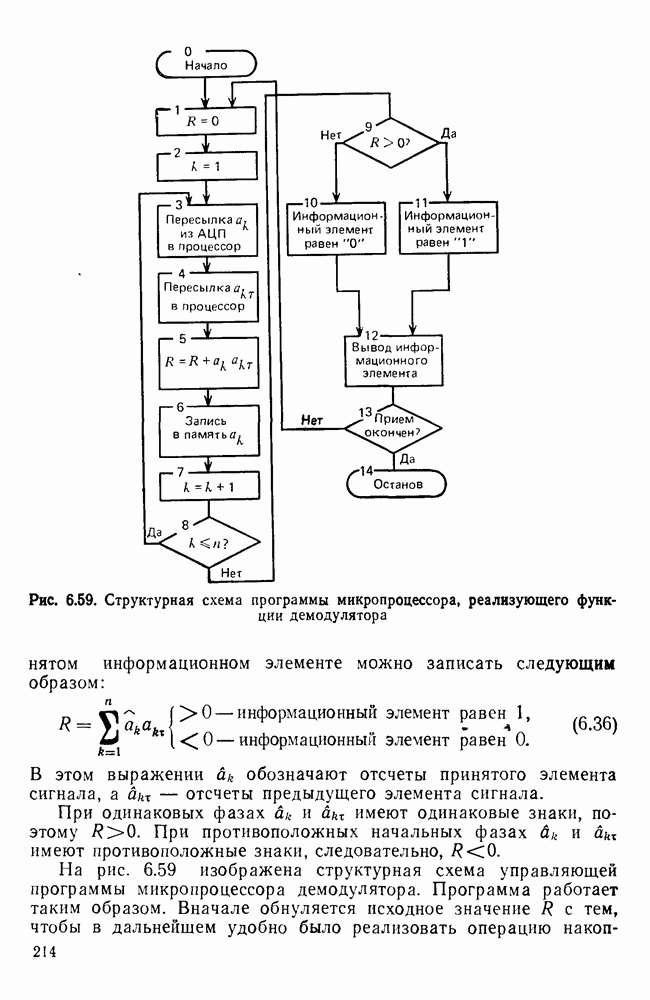
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
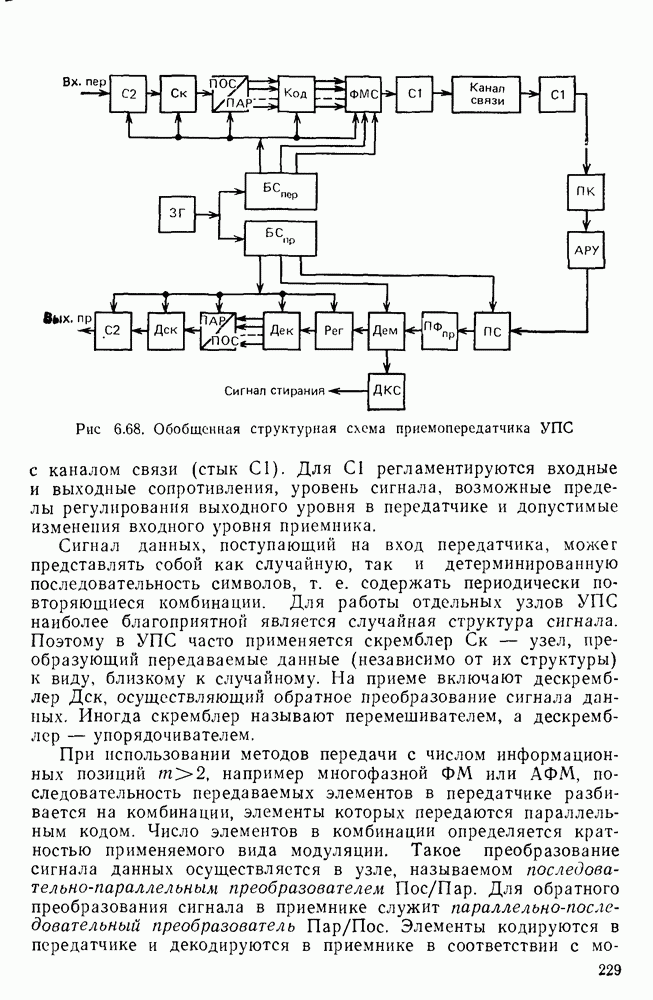
- Примеры УПС. Рекомендации МККТТ по построению УПС.
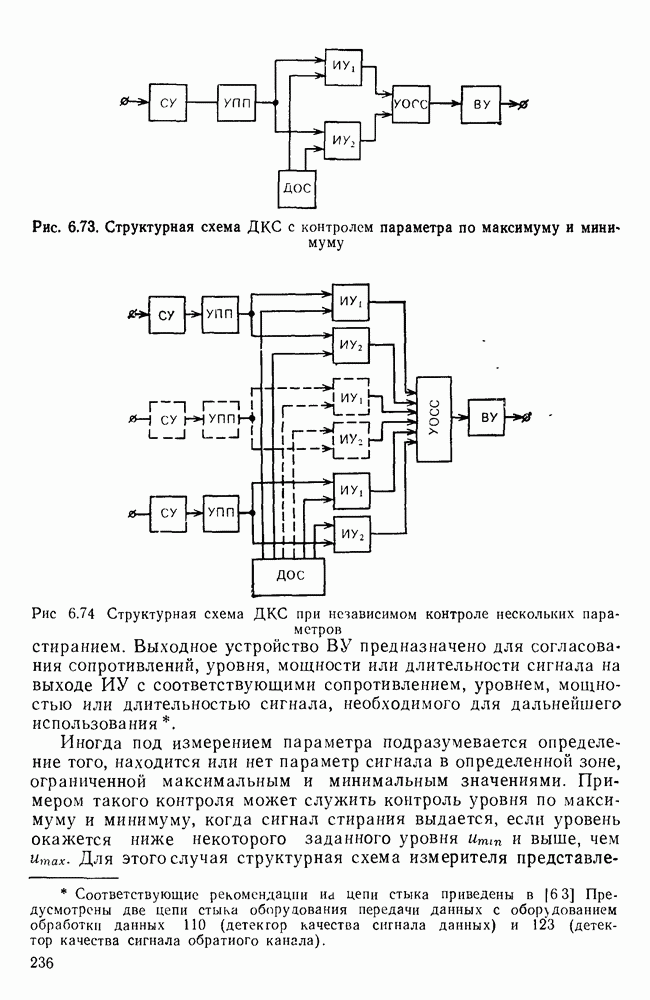
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
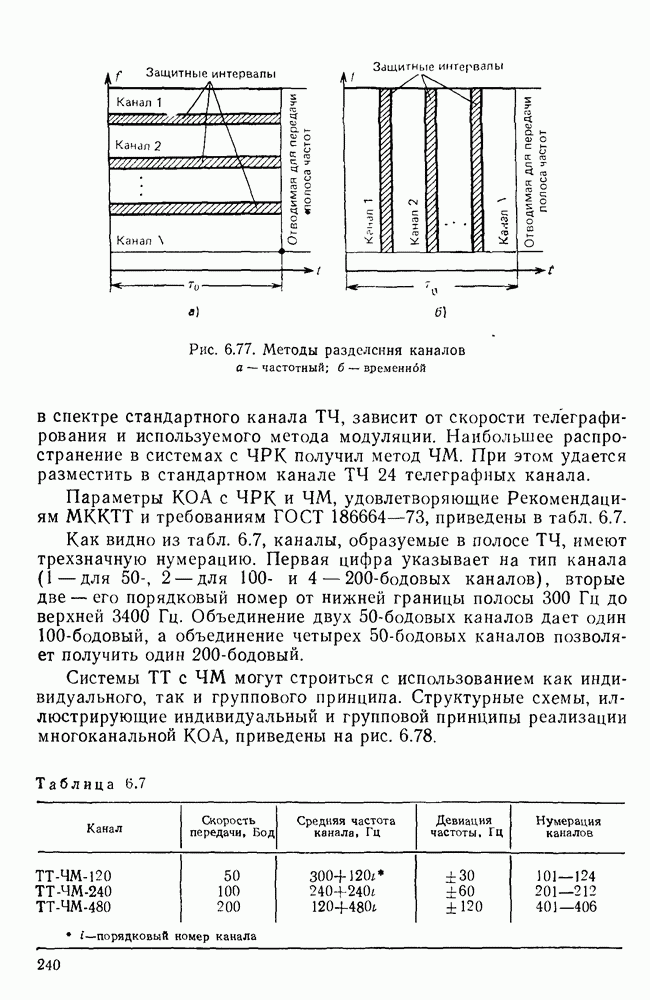
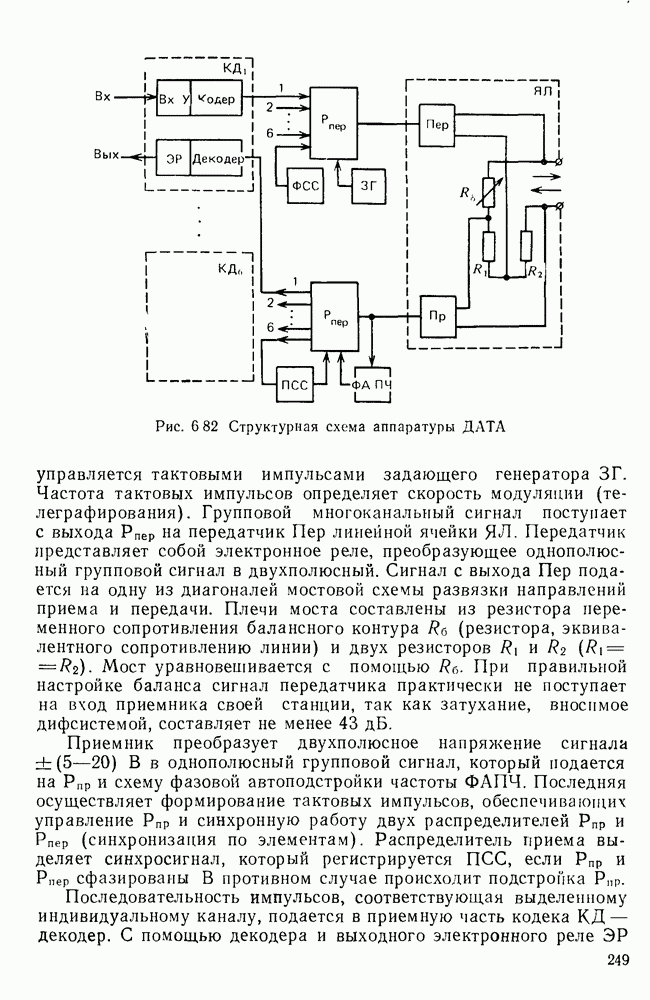
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
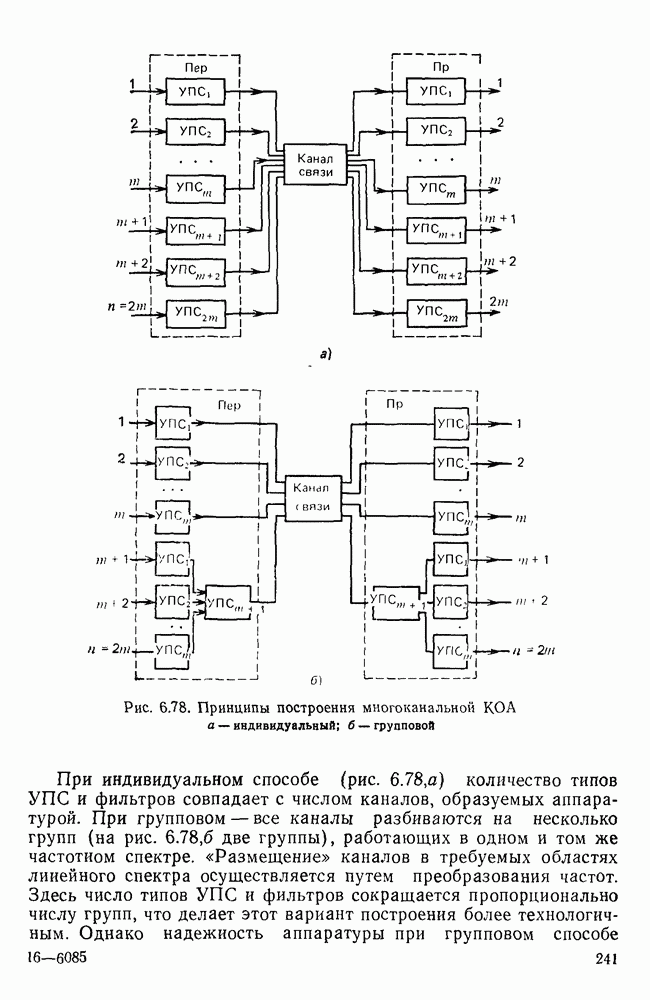
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
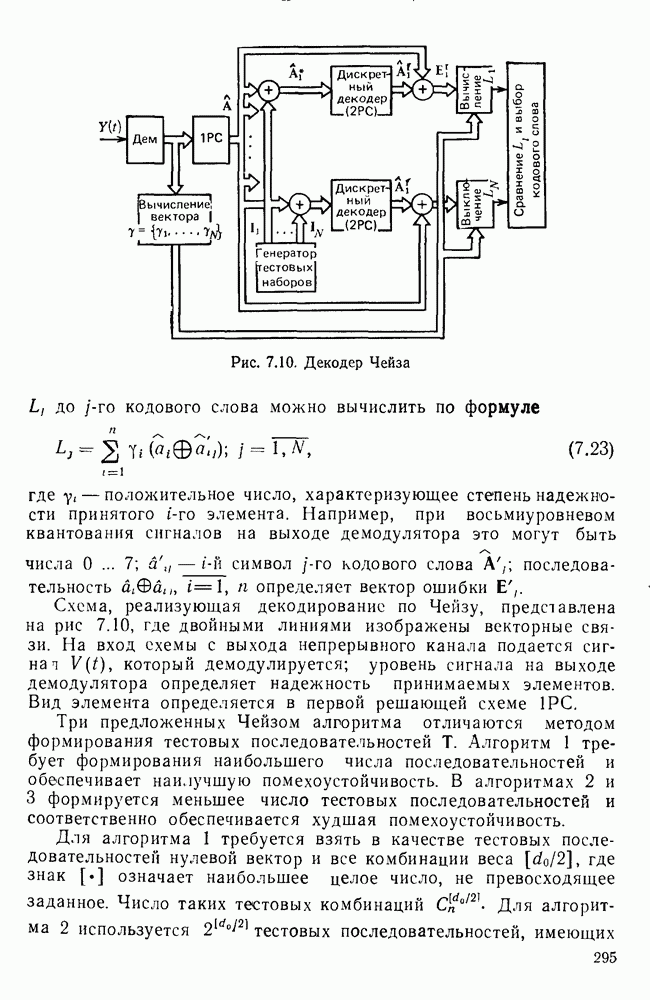
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
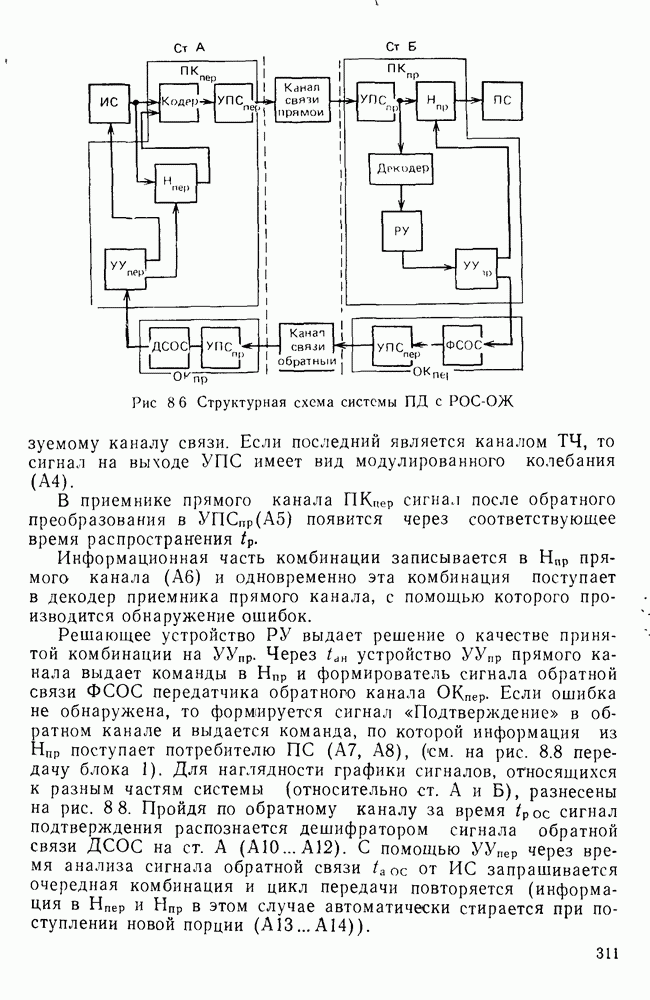
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
- Система с РОС и адресным переспросом РОС-АП.
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
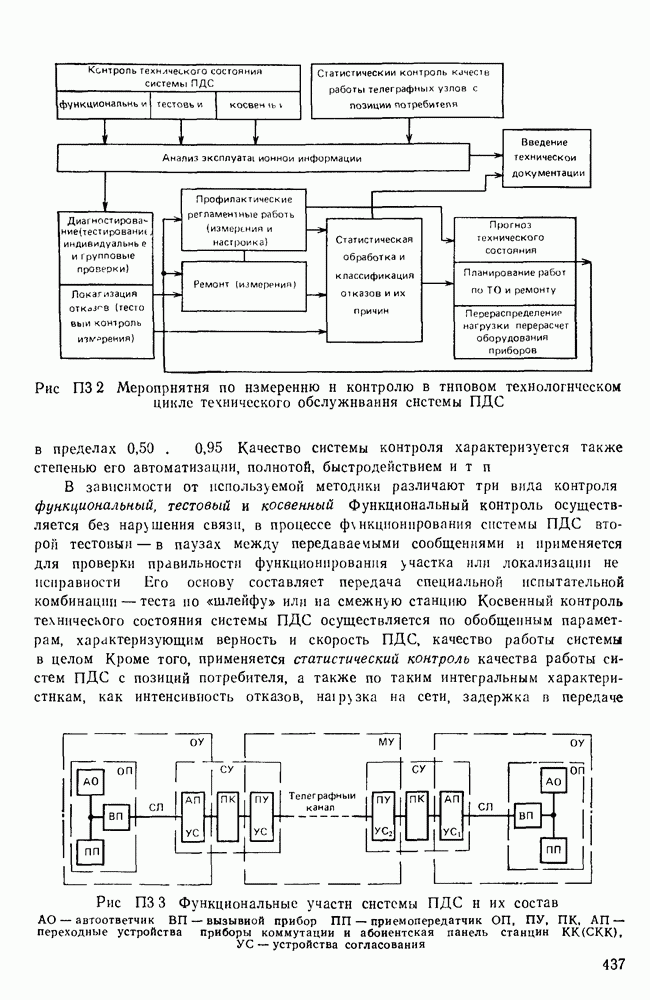
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ