| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
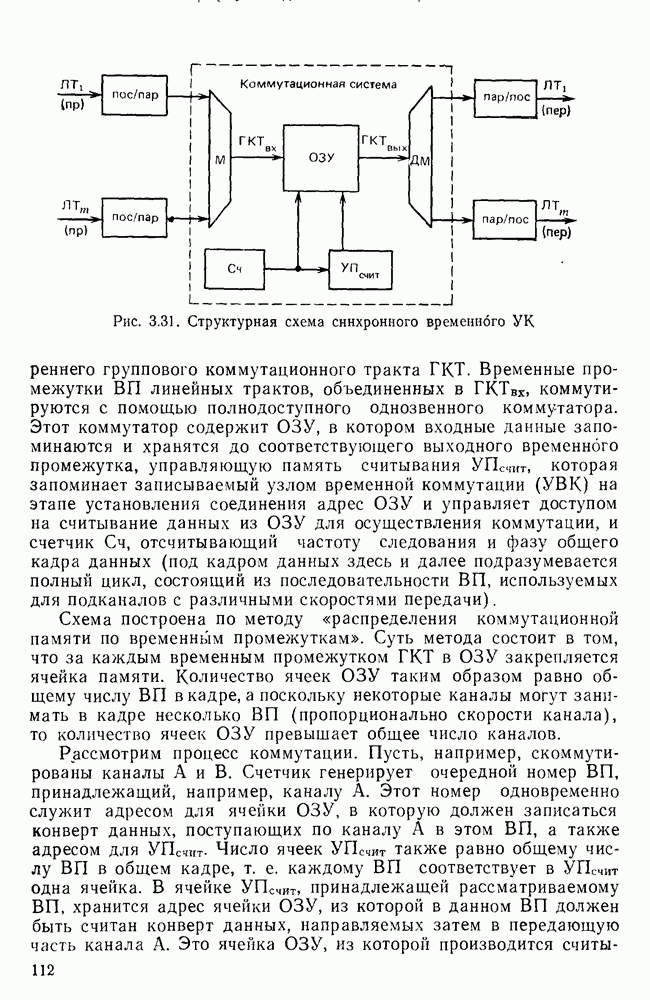
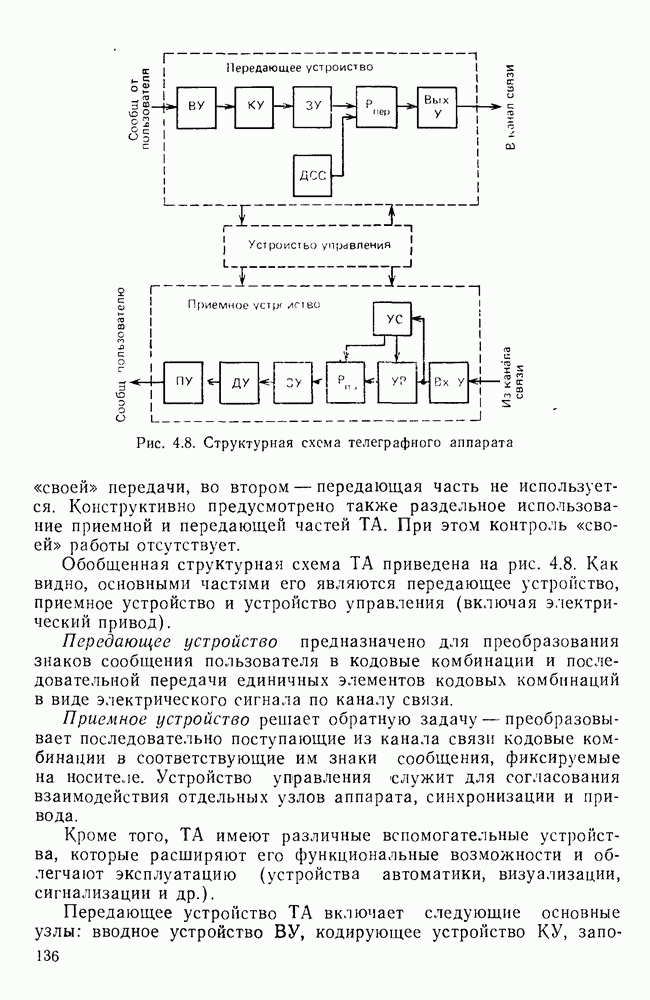
Импульсы постоянного тока.
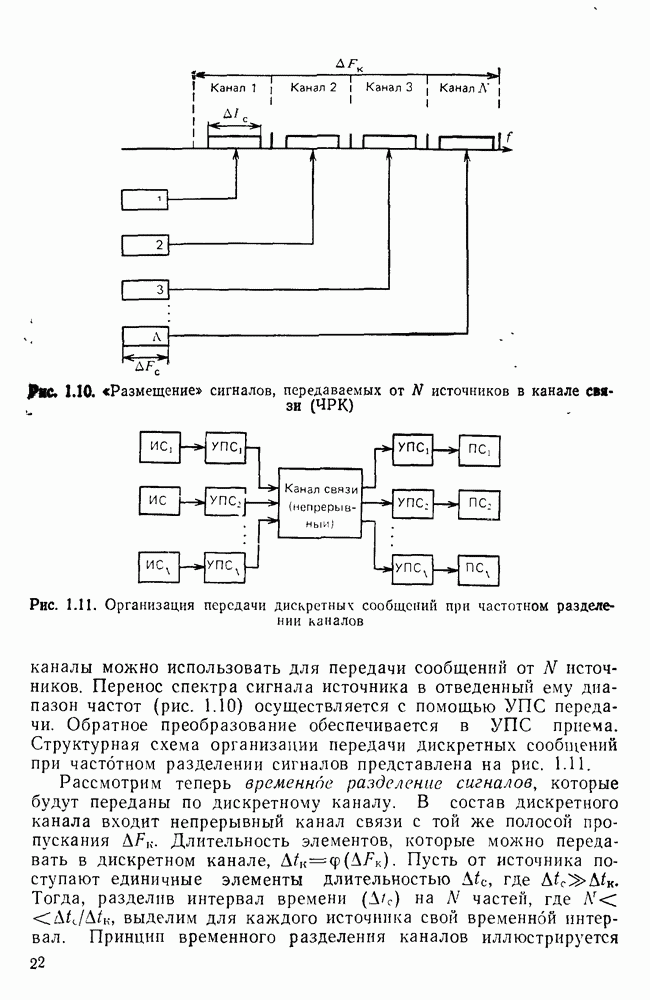
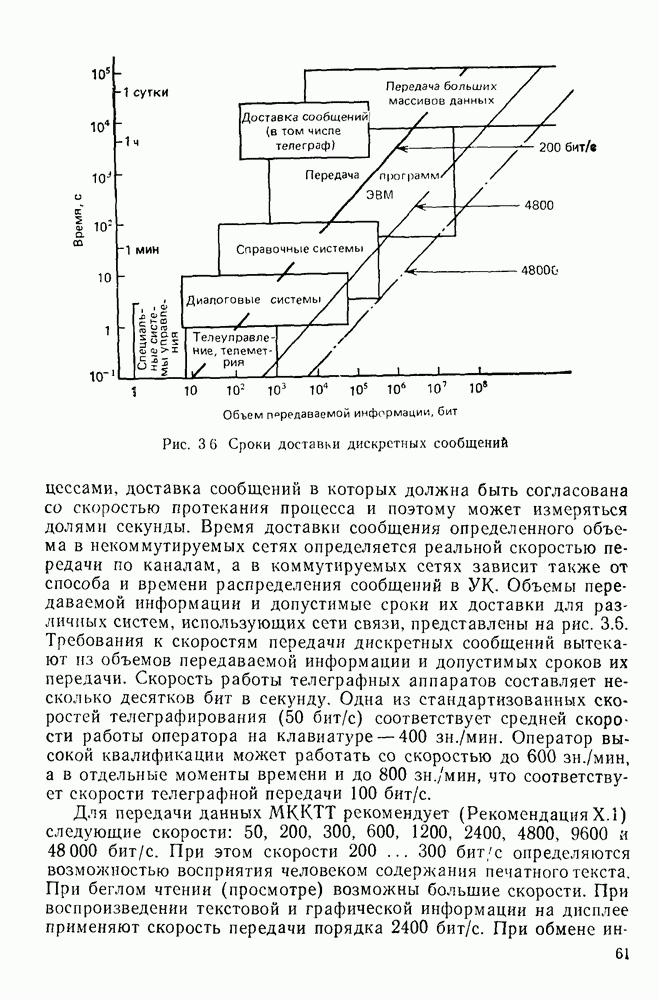
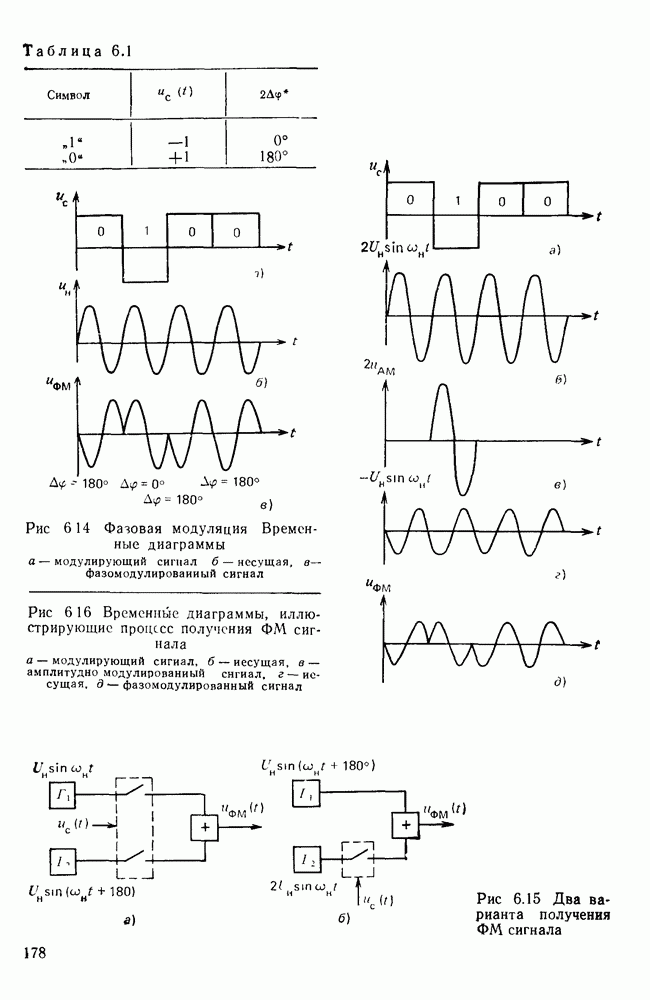
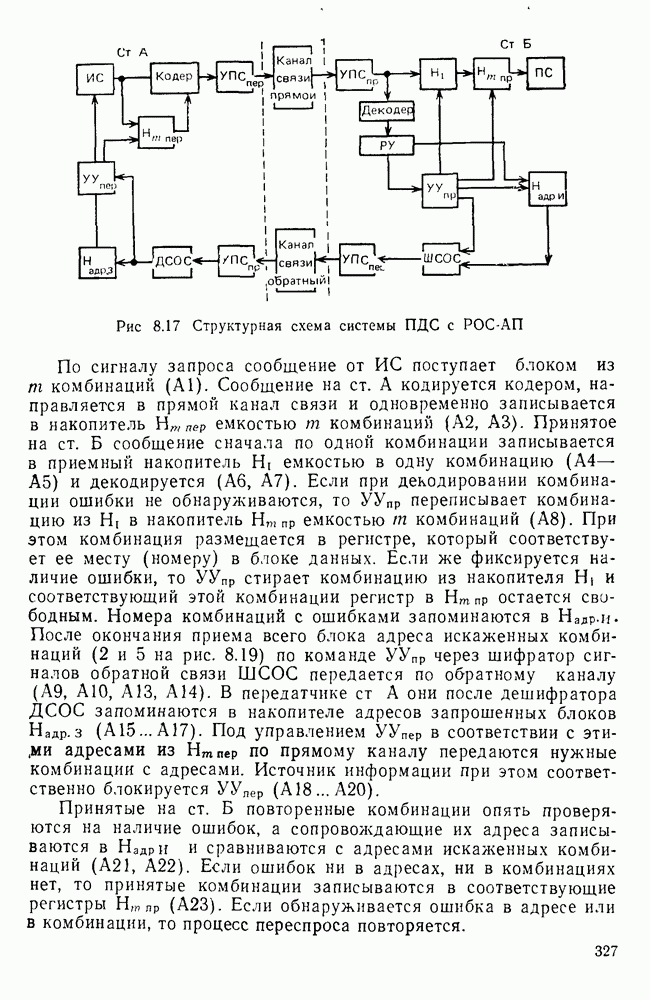
Типичным примером импульсов прямоугольной формы служат первичные телеграфные сигналы и сигналы передачи данных, называемые также импульсами постоянного тока. Они имеют вид последовательностей двух- или однополярных прямоугольных импульсов (рис. 6.1, а).
Найдем спектр периодической последовательности однополярных импульсов с периодом  и амплитудой UQ. Такая последовательность может быть представлена в виде ряда Фурье:
и амплитудой UQ. Такая последовательность может быть представлена в виде ряда Фурье:

где  — круговая частота повторения или первая гармоника (спектральная составляющая) сигнала
— круговая частота повторения или первая гармоника (спектральная составляющая) сигнала 

Рис. 6.1 Последовательность импульсов (а) и ее спектр (б)
Коэффициенты  определяют так называемый спектр амплитуд, а
определяют так называемый спектр амплитуд, а  спектр фаз. При этом [1.3]
спектр фаз. При этом [1.3]

где  — скважность импульсной последовательности. Постоянная составляющая или среднее значение сигнала
— скважность импульсной последовательности. Постоянная составляющая или среднее значение сигнала  за период
за период  Спектр амплитуд для случая
Спектр амплитуд для случая  представлен на рис.
представлен на рис. 
Спектр периодической последовательности однополярных импульсов при  содержит кроме постоянной составляющей составляющие с частотами
содержит кроме постоянной составляющей составляющие с частотами  и т. д. Разность между этими спектральными составляющими
и т. д. Разность между этими спектральными составляющими  (С ростом Т уменьшается, при этом сами составляющие также уменьшаются по амплитуде. При
(С ростом Т уменьшается, при этом сами составляющие также уменьшаются по амплитуде. При  сигнал становится непериодическим, а спектр — непрерывным. Вместо понятия спектра амплитуд при этом вводится понятие спектральной плотности. Спектральная плотность определяется как отношение «амплитуды спектральной составляющей» к бесконечно малой полосе частот
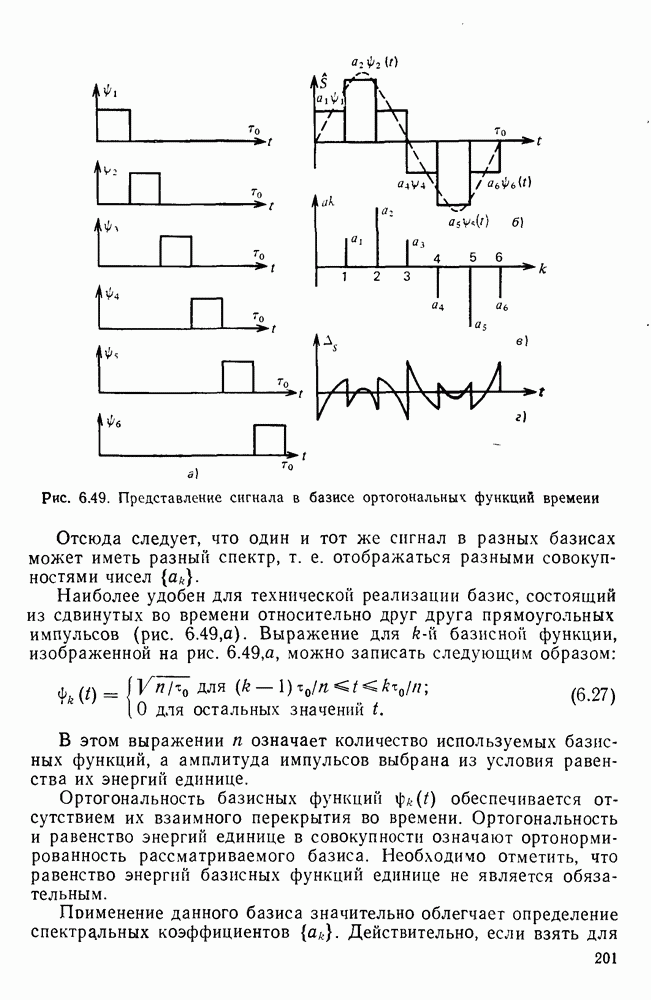
сигнал становится непериодическим, а спектр — непрерывным. Вместо понятия спектра амплитуд при этом вводится понятие спектральной плотности. Спектральная плотность определяется как отношение «амплитуды спектральной составляющей» к бесконечно малой полосе частот  и вычисляется через интеграл Фурье [1.1]:
и вычисляется через интеграл Фурье [1.1]:

где  — спектральная плотность амплитуд;
— спектральная плотность амплитуд;  - спектр фаз.
- спектр фаз.
Зная  можно найти
можно найти  используя обратное преобразование Фурье:
используя обратное преобразование Фурье:

Спектральная плотность амплитуд одиночного прямоугольного импульса с точностью до множителя  изображена штриховой линией на рис.
изображена штриховой линией на рис. 
Спектр периодической последовательности импульсов и одиночного импульса содержит составляющие с частотой от 0 до бесконечности, т. е. является бесконечным. Если последовательность прямоугольных импульсов передается по каналу связи, который всегда пропускает только ограниченный спектр, то форма сигнала на выходе канала изменяется. Форму сигнала можно определить, используя обратное преобразование Фурье (6.6).
На практике под шириной спектра сигнала обычно понимают ту область частот, в которой сосредоточена основная энергия сигнала. При этом вводится понятие эффективной ширины спектра сигнала. На рис.  — это диапазон частот от 0 до
— это диапазон частот от 0 до  в котором сосредоточено около 90% энергии сигнала. Значит, чем меньше длительность импульса (выше скорость телеграфирования
в котором сосредоточено около 90% энергии сигнала. Значит, чем меньше длительность импульса (выше скорость телеграфирования  ), тем шире спектр. В частности, бесконечно короткий импульс имеет бесконечно протяженный спектр с равномерной плотностью. Таким образом, передача с более высокой скоростью требует каналов с более широкой полосой пропускания.
), тем шире спектр. В частности, бесконечно короткий импульс имеет бесконечно протяженный спектр с равномерной плотностью. Таким образом, передача с более высокой скоростью требует каналов с более широкой полосой пропускания.
При заданной длительности единичного элемента то на спектр передаваемого сигнала оказывают влияние два фактора. Один из них — форма импульса, которую следует тщательно выбирать для получения хорошего (компактного) спектра сигнала. Другой фактор — характер передаваемой цифровой последовательности, т. е. спектр зависит от статистических характеристик передаваемой последовательности, и ее перекодированием спектр можно изменить.
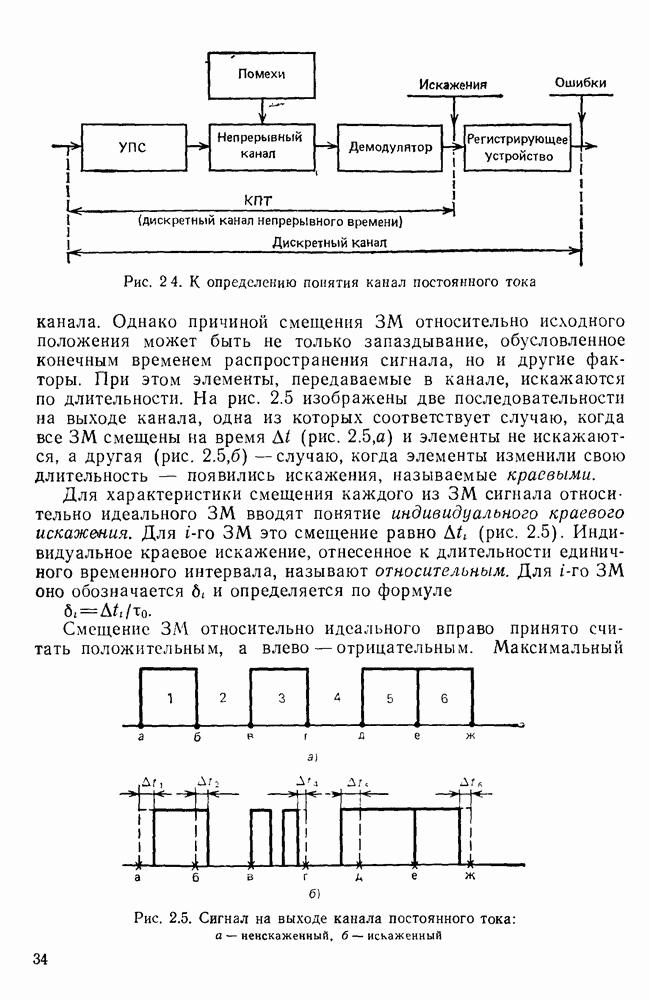
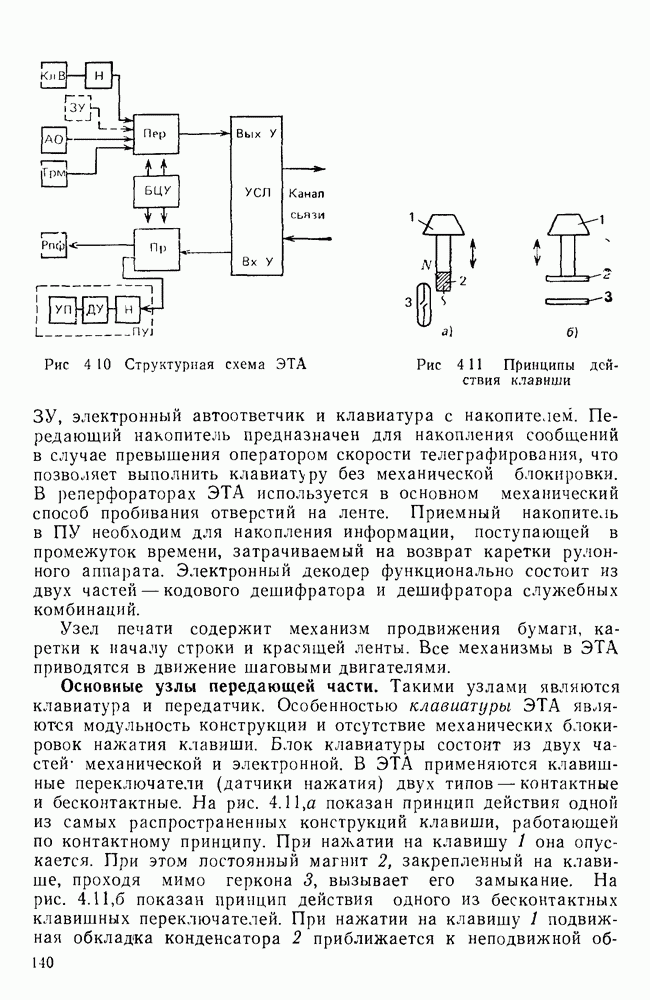
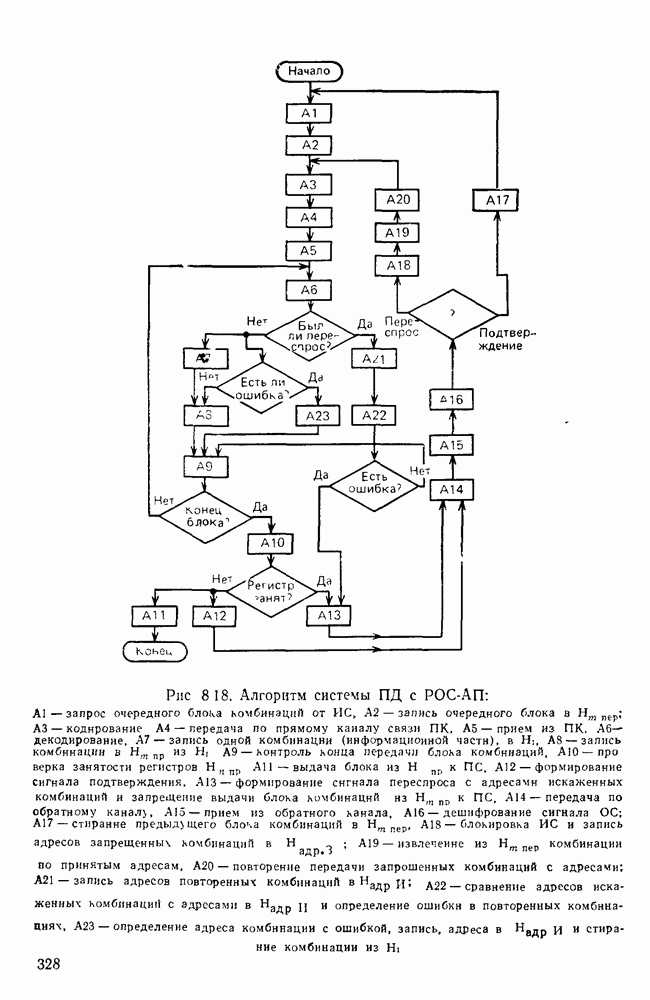
Для оценки искажений импульсов постоянного тока, вызванных ограничением спектра, рассмотрим прохождение импульса через идеальный фильтр нижних частот (ФНЧ). В качестве входного воздействия воспользуемся ступенчатой функцией

представленной графически на рис. 6.2. Выбор такого входного воздействия обусловлен тем, что, во-первых, его использование упрощает математические выкладки, во-вторых, одиночный прямоугольный импульс конечной длительности можно представить как последовательность двух единичных скачков напряжения противоположного знака, сдвинутых во времени на величину, равную длительности импульса (рис. 6.3).

Рис. 6.2 Ступенчатая функция

Рис. 6.3. Представление одиночного импульса

Рис. 6.4. Характеристика идеального ФНЧ
И, наконец, зная характеристику устанавливающегося процесса при воздействии единичного скачка, с помощью теоремы свертывания можно найти устанавливающийся процесс для произвольной формы воздействия [1.1].
Пусть на вход идеального ФНЧ с частотой среза  амплитудно- и фазочастотная характеристики которого имеют вид (рис. 6.4):
амплитудно- и фазочастотная характеристики которого имеют вид (рис. 6.4):

где  — групповое время прохождения фильтра, в момент
— групповое время прохождения фильтра, в момент  подается сигнал (6.7), который может быть представлен в виде [1.3]
подается сигнал (6.7), который может быть представлен в виде [1.3]

Для получения сигнала на выходе ФНЧ умножим все компоненты входного сигнала на модуль коэффициента передачи фильтра и вычтем из аргумента синуса сдвиг фаз на каждой из частот:

Подставив в (6.9) значение коэффициента передачи из (6.8), получим


Рис. 6.5 Сигнал на выходе ФПЧ

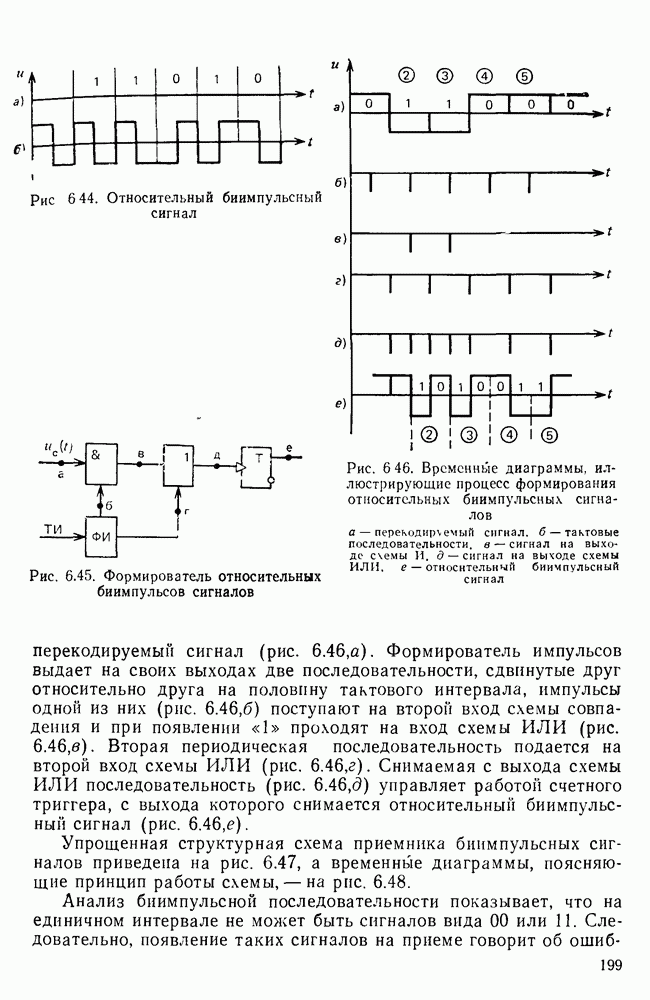
Рис. 6.6 Перекодирование сигналов с введением избыточности а — исходная последовательность; б — биимпульсный сигнал, в — биполярный сигнал
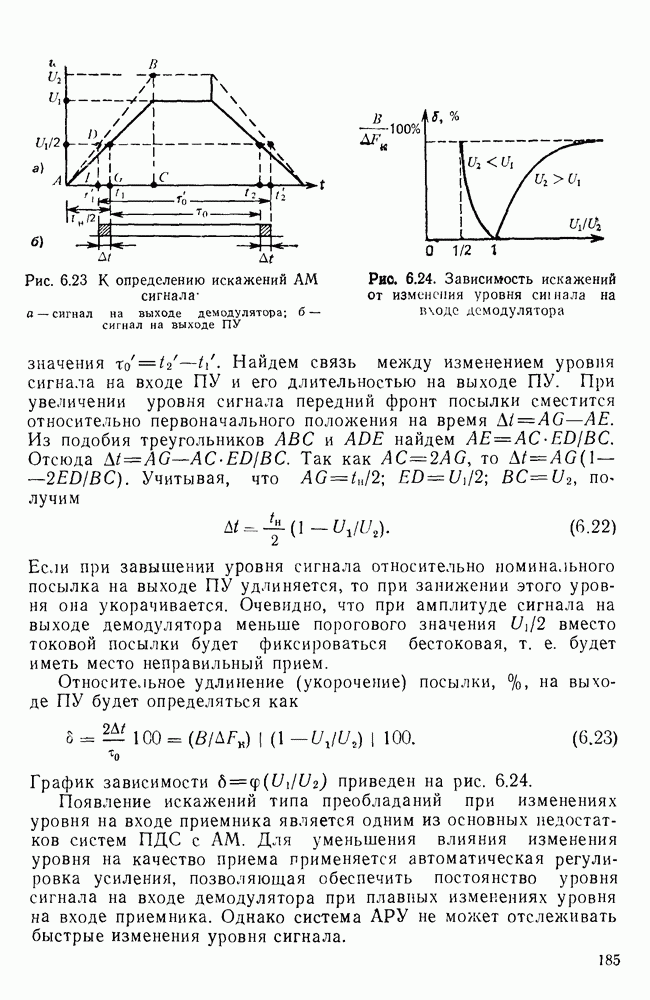
На рис. 6.5 представлен вид сигнала на выходе ФНЧ, рассчитанный по формуле (6.10). Время нарастания переходного процесса  можно определить из треугольника ABC, в котором АС является касательной в точке
можно определить из треугольника ABC, в котором АС является касательной в точке 

где

Учитывая (6.12), получим  Таким образом, время нарастания обратно пропорционально граничной частоте идеального ФНЧ.
Таким образом, время нарастания обратно пропорционально граничной частоте идеального ФНЧ.
Интересно отметить связь полученной формулы с так называемым условием Найквиста, ограничивающим скорость передачи двоичных сигналов сверху:  Бод. Учитывая, что
Бод. Учитывая, что  имеем Хотт
имеем Хотт  Следовательно, длительность единичного элемента в соответствии с условием Найквиста должна быть не менее, чем время нарастания переходного процесса, т. е.
Следовательно, длительность единичного элемента в соответствии с условием Найквиста должна быть не менее, чем время нарастания переходного процесса, т. е. 
Вид сигнала на выходе ФНЧ зависит от его АЧХ и ФЧХ Так, чем плавнее переход АЧХ фильтра от полосы пропускания к полосе задержания, тем меньше колебательные выбросы переходного процесса. Отклонение ФЧХ от идеальной приводит к удлинению переходного процесса и, как следствие, к взаимному влиянию импульсов или своеобразной помехе, называемой в литературе межеимвольной или интерференционной [6.2].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Виды сигналов.
- Структурная схема системы ПДС.
- Способы передачи и обработки сигналов в системах ПДС.
- Объединение и разделение сигналов в системах ПДС.
- Понятие о цепях стыка.
- 1.2. ВНЕШНИЕ И ВНУТРЕННИЕ ПАРАМЕТРЫ СИСТЕМЫ ПДС. ОПТИМИЗАЦИЯ СИСТЕМЫ ПДС
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 2. СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ХАРАКТЕРИСТИКИ КАНАЛОВ
- 2.1. НЕПРЕРЫВНЫЙ КАНАЛ
- 2.2. ДИСКРЕТНЫЙ КАНАЛ НЕПРЕРЫВНОГО ВРЕМЕНИ И РЕГИСТРАЦИЯ СИГНАЛОВ
- 2.3. ДИСКРЕТНЫЙ КАНАЛ. СТАТИСТИКА ОШИБОК В ДВОИЧНОМ ДИСКРЕТНОМ КАНАЛЕ
- 2.4. РАСШИРЕННЫЙ ДИСКРЕТНЫЙ КАНАЛ
- Понятие о корректирующих кодах.
- Эффективность применения корректирующих кодов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 3. СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
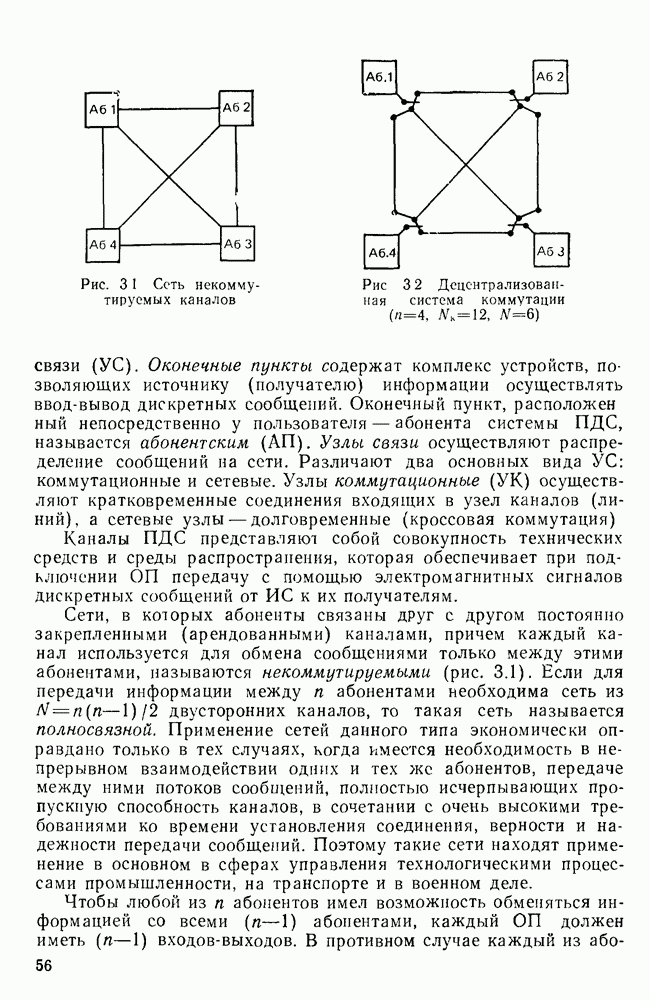
- 3.1. НЕКОММУТИРУЕМЫЕ И КОММУТИРУЕМЫЕ СЕТИ ПДС
- 3.2. ТРЕБОВАНИЯ К СЕТЯМ ПДС
- 3.3. СПОСОБЫ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СООБЩЕНИЙ
- Синхронное временное распределение (СВРп).
- Асинхронное временное распределение (АВРп).
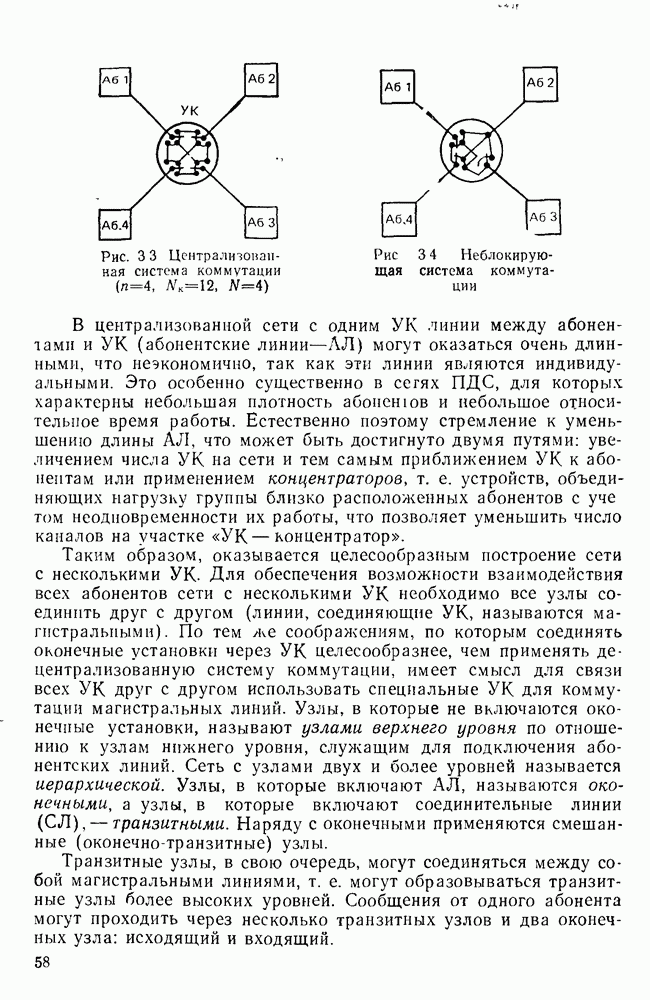
- 3.4. СИСТЕМЫ КОММУТАЦИИ В СЕТЯХ ПДС
- 3.5. УПРАВЛЕНИЕ В СЕТЯХ ПДС
- 3.6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ КОММУТАЦИИ
- 3.7. СЕТЬ ТЕЛЕГРАФНОЙ СВЯЗИ
- Сеть абонентского телеграфирования.
- 3.8. СЕТИ ПЕРЕДАЧИ ДАННЫХ
- Сеть ПД с КП.
- 3.9. УЗЛЫ КОММУТАЦИИ В СЕТЯХ ПДС
- Электронная станция коммутации ЭСК-А.
- Перспективные УК для синхронной сети.
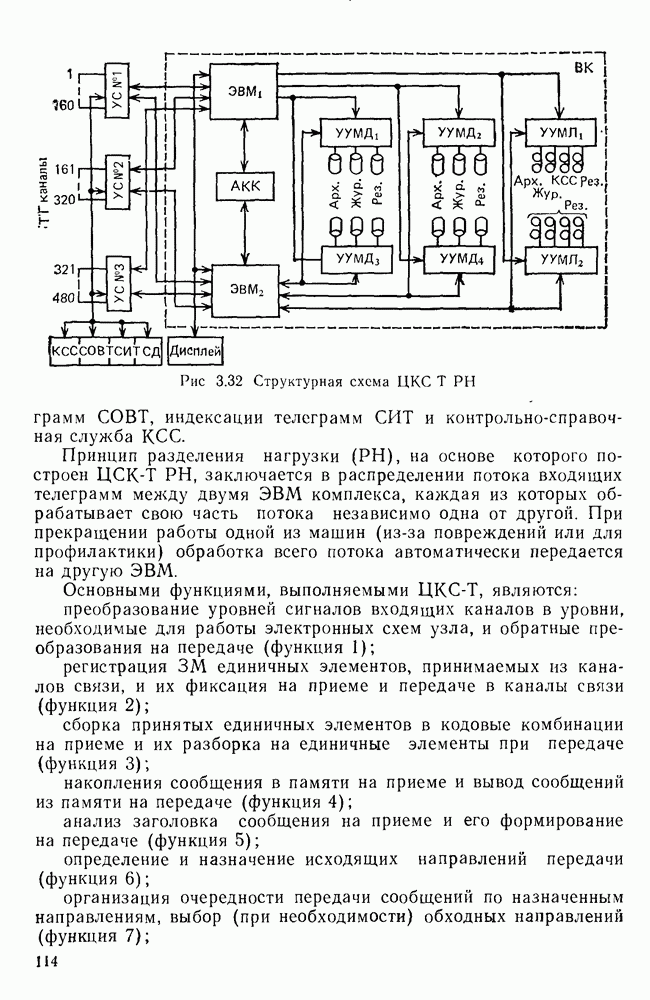
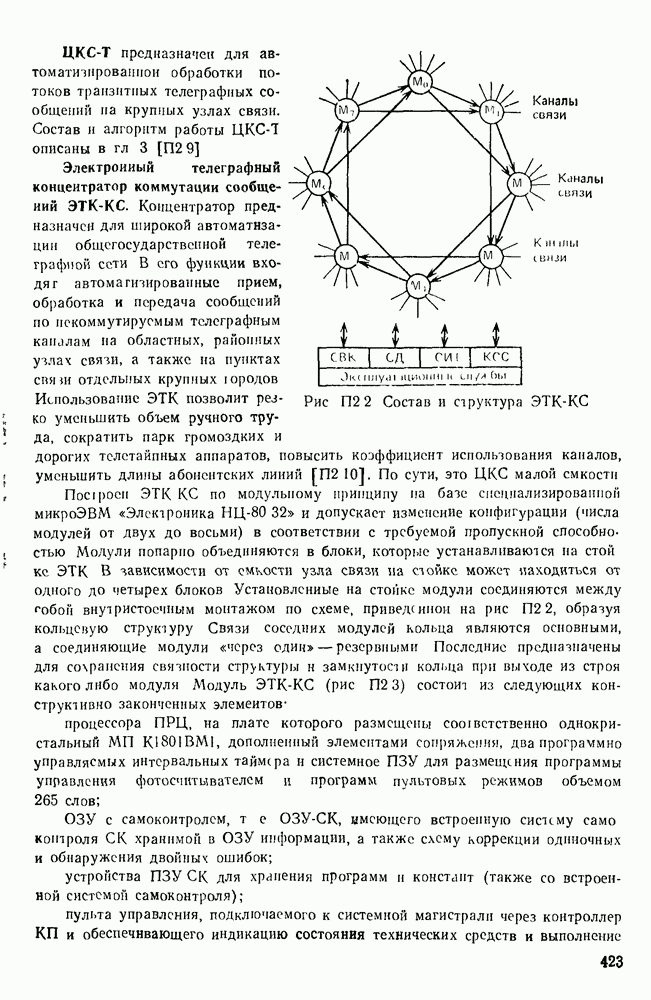
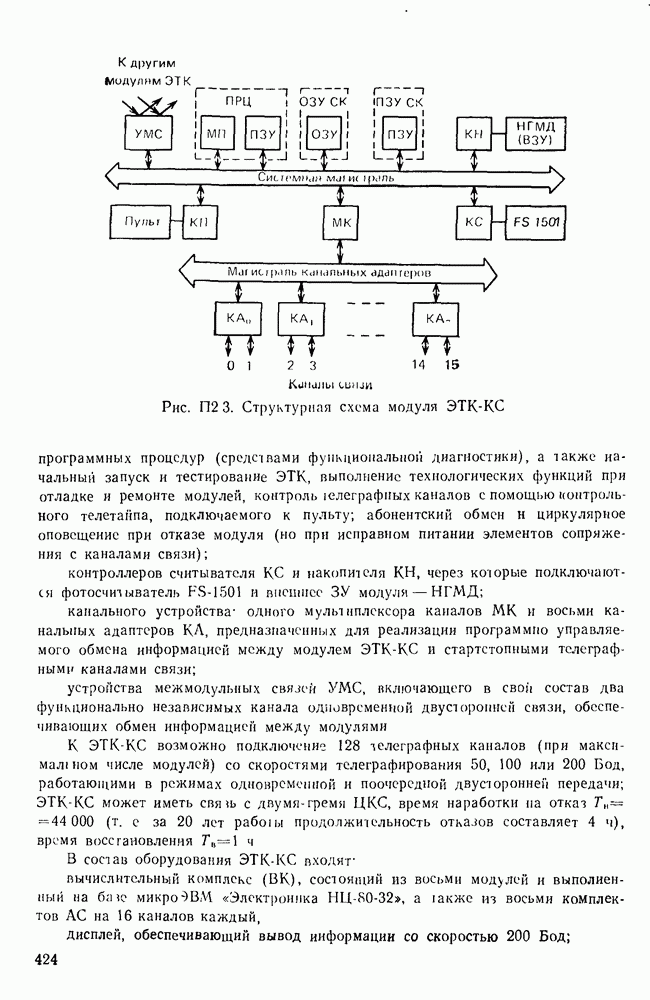
- Современные телеграфные узлы (центры) КС (ЦКС-Т).
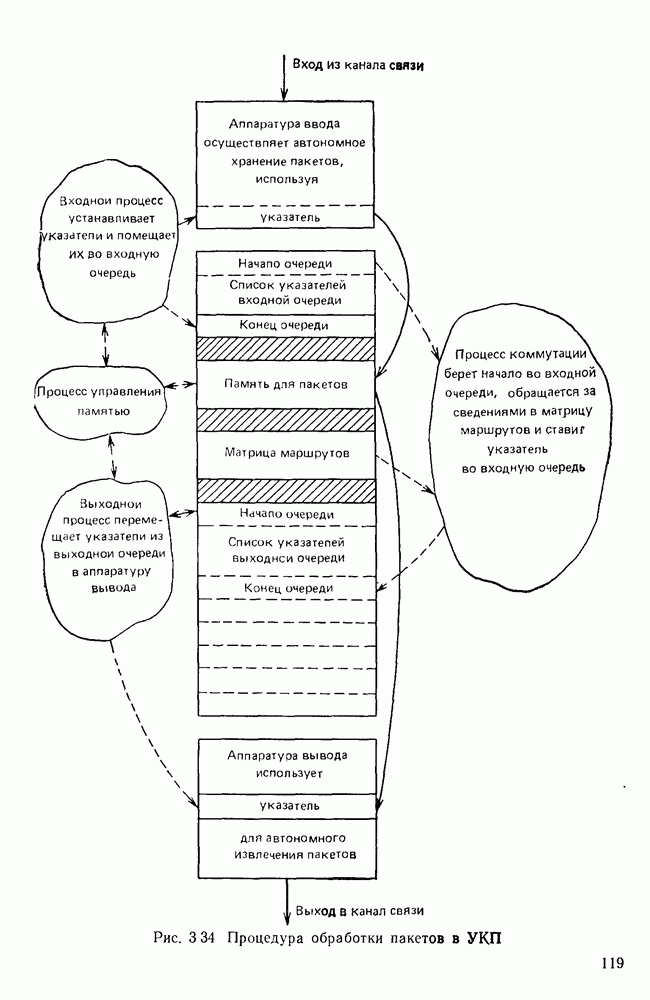
- Узлы коммутации пакетов.
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 4. ОКОНЕЧНЫЕ УСТРОЙСТВА СИСТЕМ ПДС
- 4.1. АБОНЕНТСКИЕ ОКОНЕЧНЫЕ ПУНКТЫ
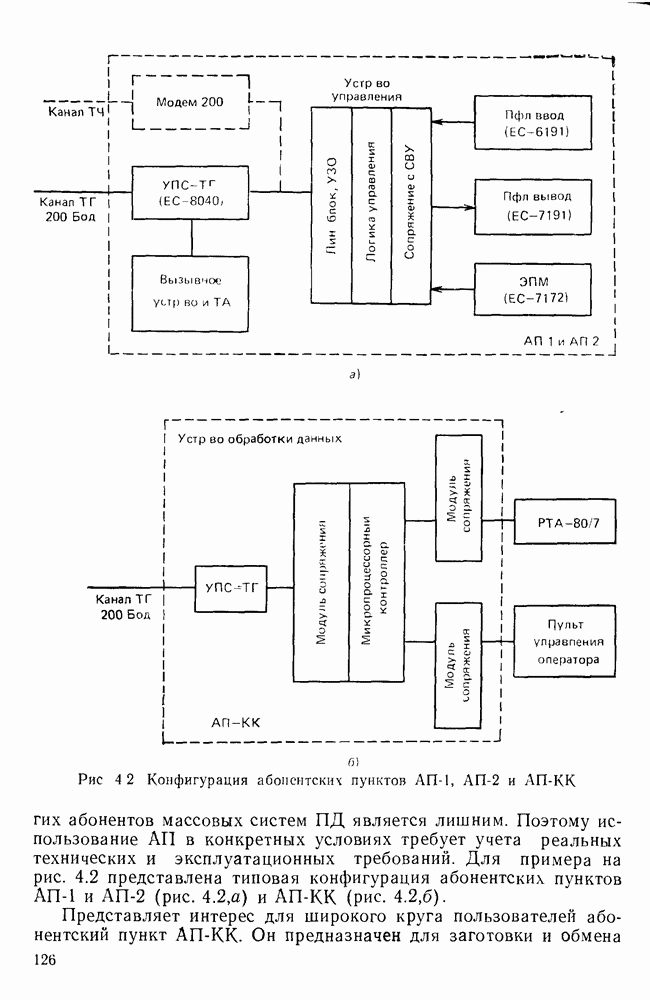
- Абонентские пункты передачи данных (АП-ПД).
- 4.2. ВВОДНО ВЫВОДНЫЕ УСТРОЙСТВА АП
- Регистрирующие устройства с деформацией носителя.
- Регистрирующие устройства без деформации носителя.
- Терминалы.
- Устройства считывания.
- 4.3. ЭЛЕКТРОННЫЙ ТЕЛЕГРАФНЫЙ АППАРАТ
- Основные узлы передающей части.
- Основные узлы приемной части.
- 4.4. ИСПРАВЛЯЮЩАЯ СПОСОБНОСТЬ ТЕЛЕГРАФНОГО АППАРАТА
- 4.5. РЕКОМЕНДАЦИИ МККТТ ПО ОКОНЕЧНОЙ АППАРАТУРЕ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 5. МЕТОДЫ СОПРЯЖЕНИЯ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ С ДИСКРЕТНЫМ КАНАЛОМ
- 5.2. ОСНОВЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ
- Кодовое дерево для множества кодовых слов.
- 5.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ ИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- Метод Хафмена.
- Равномерное по выходу кодирование.
- 5.4. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ПРИ НЕИЗВЕСТНОЙ СТАТИСТИКЕ СООБЩЕНИЙ
- 5.5. СОПРЯЖЕНИЕ ИСТОЧНИКОВ ДИСКРЕТНЫХ СООБЩЕНИЙ С СИНХРОННЫМ ДИСКРЕТНЫМ КАНАЛОМ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
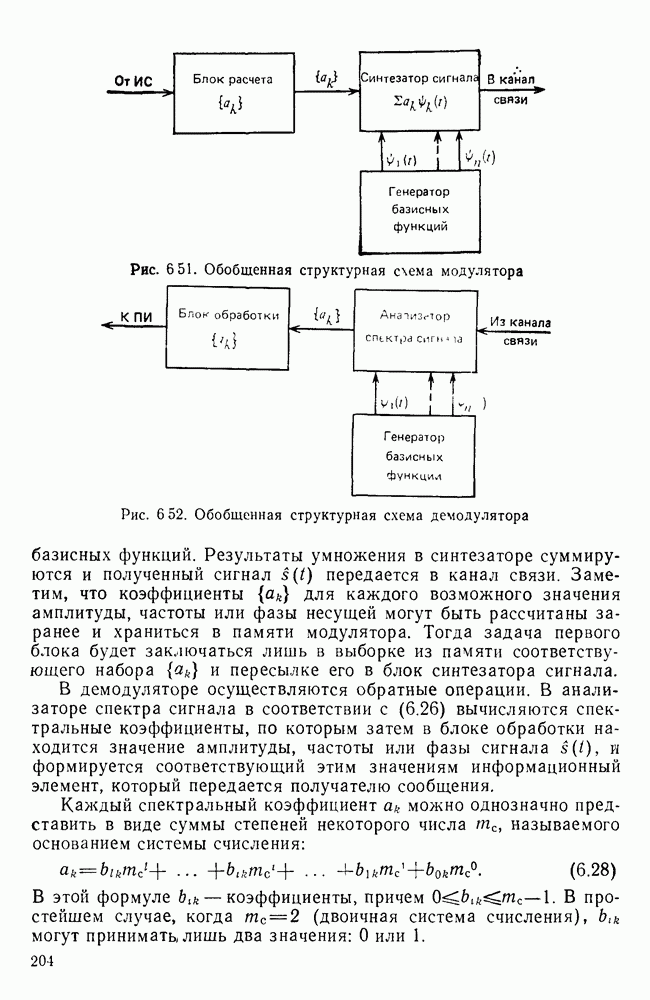
- Глава 6. МЕТОДЫ И УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.1. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ УСТРОЙСТВ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
- 6.2. СИГНАЛЫ, ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ ПДС. СВОЙСТВА СИГНАЛОВ
- Импульсы постоянного тока.
- Перекодирование первичных сигналов с введением избыточности.
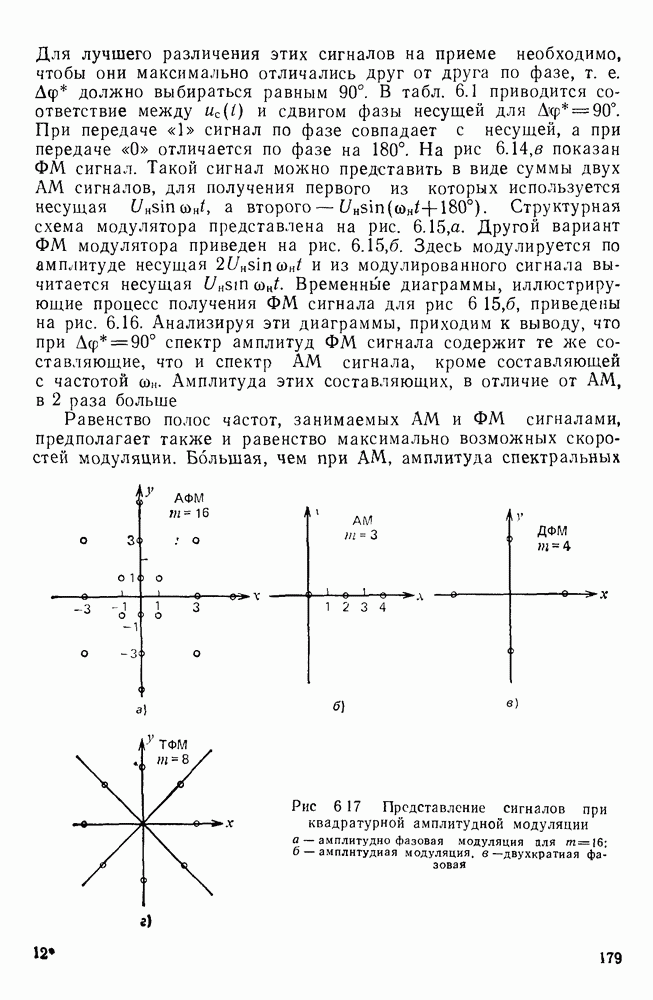
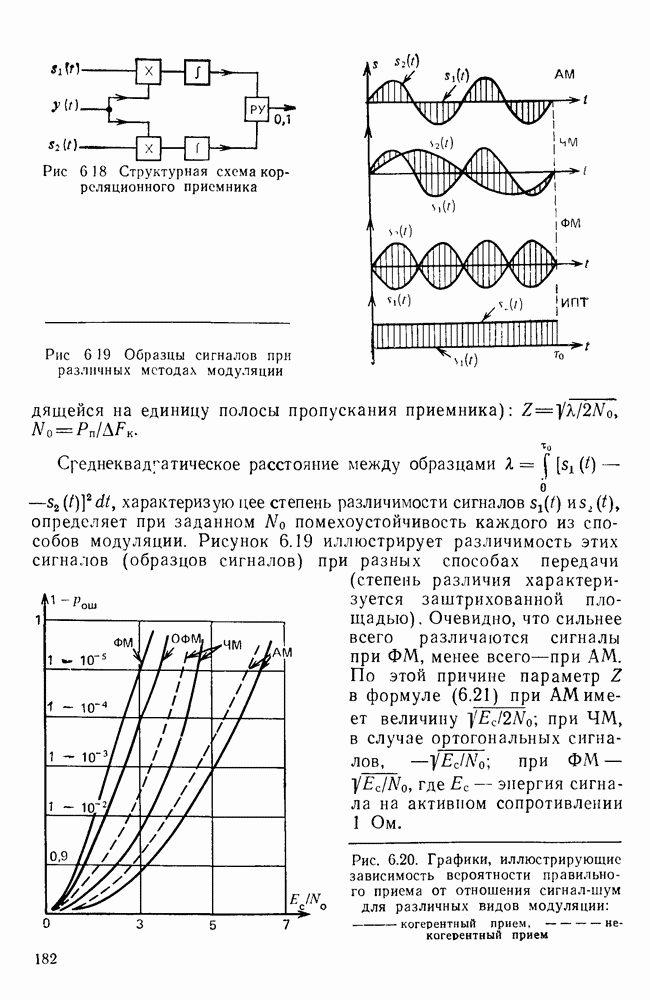
- Модулированные сигналы.
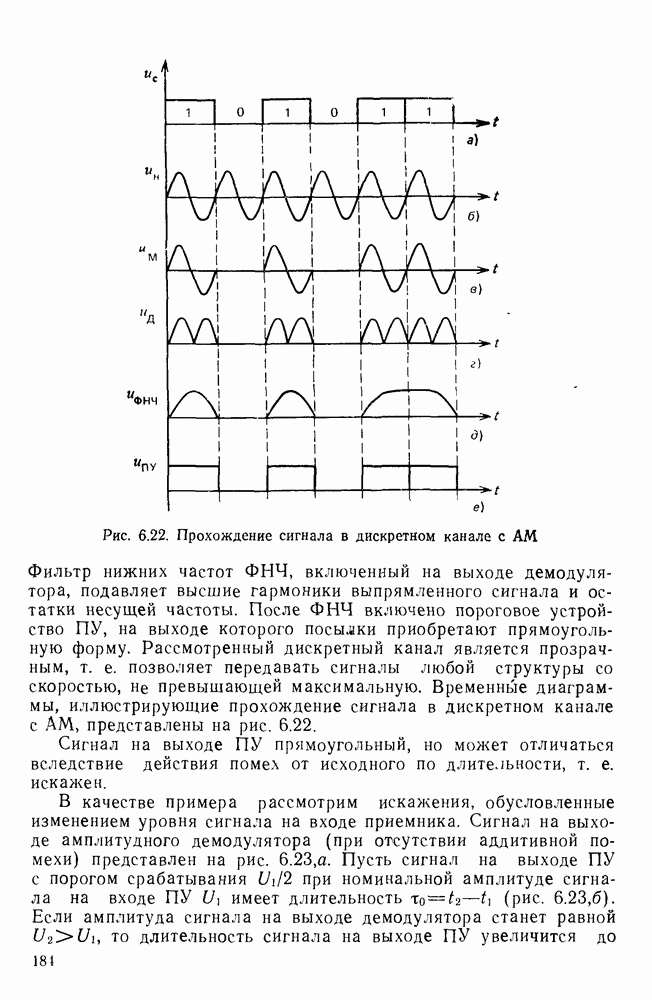
- 6.3. ОПТИМАЛЬНЫЙ ПРИЕМ ДИСКРЕТНЫХ СИГНАЛОВ
- 6.4. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ КАНАЛОВ
- Дискретный канал с частотной модуляцией.
- Дискретный канал с фазовой модуляцией.
- Перекодирование первичных сигналов с введением избыточности.
- 6.5. ЦИФРОВАЯ ГЕНЕРАЦИЯ И ОБРАБОТКА СИГНАЛОВ В УПС
- Представление чисел в устройствах ЦОС.
- Эффекты квантования в устройствах ЦОС.
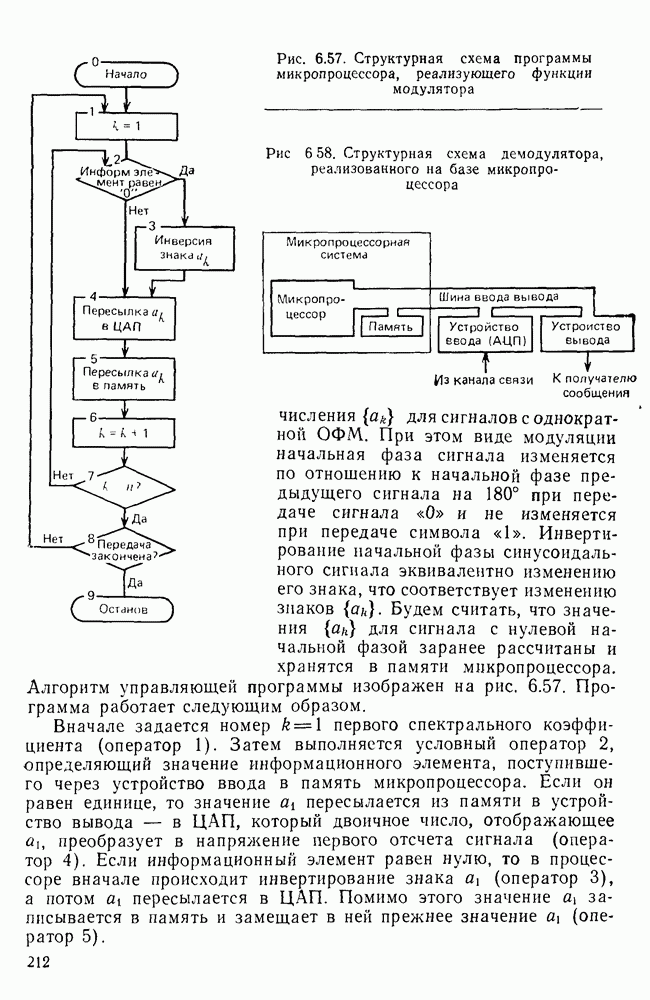
- Основы микропроцессорной реализации модуляторов УПС.
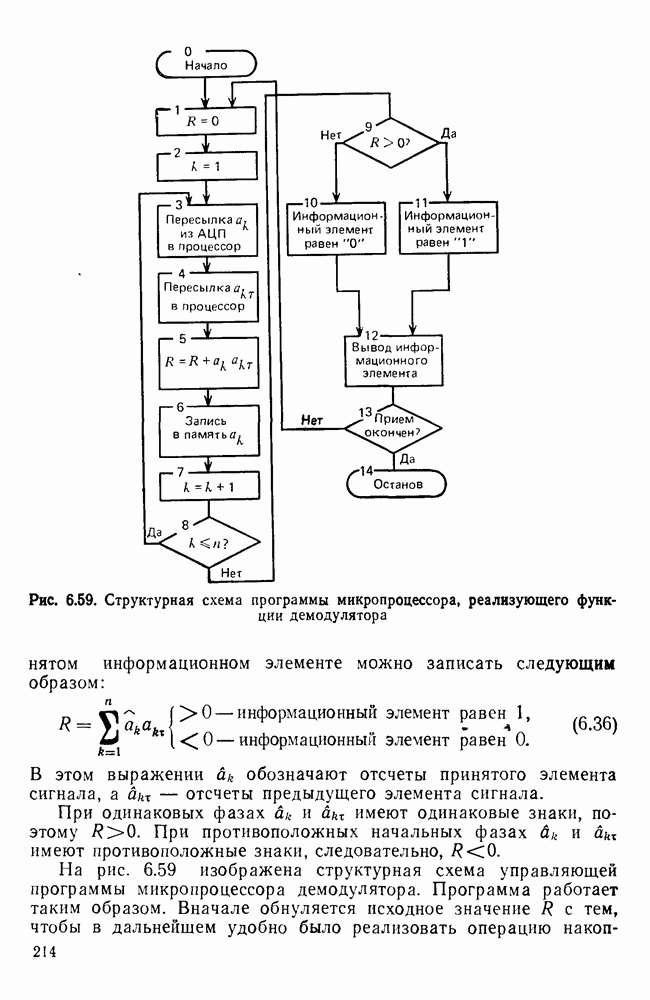
- Основы микропроцессорной реализации демодуляторов УПС.
- 6.6. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ УДЕЛЬНОЙ СКОРОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ
- Коррекция линейных искажений.
- Формирование сигналов, обеспечивающих минимизацию межсимвольных помех.
- Использование многопозиционных сигналов.
- 6.7. ОБЕСПЕЧЕНИЕ ВЫСОКОЙ ПОМЕХОУСТОЙЧИВОСТИ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ С СОСРЕДОТОЧЕННЫМИ ВО ВРЕМЕНИ ПОМЕХАМИ
- Дискретные сложные сигналы (ДСС).
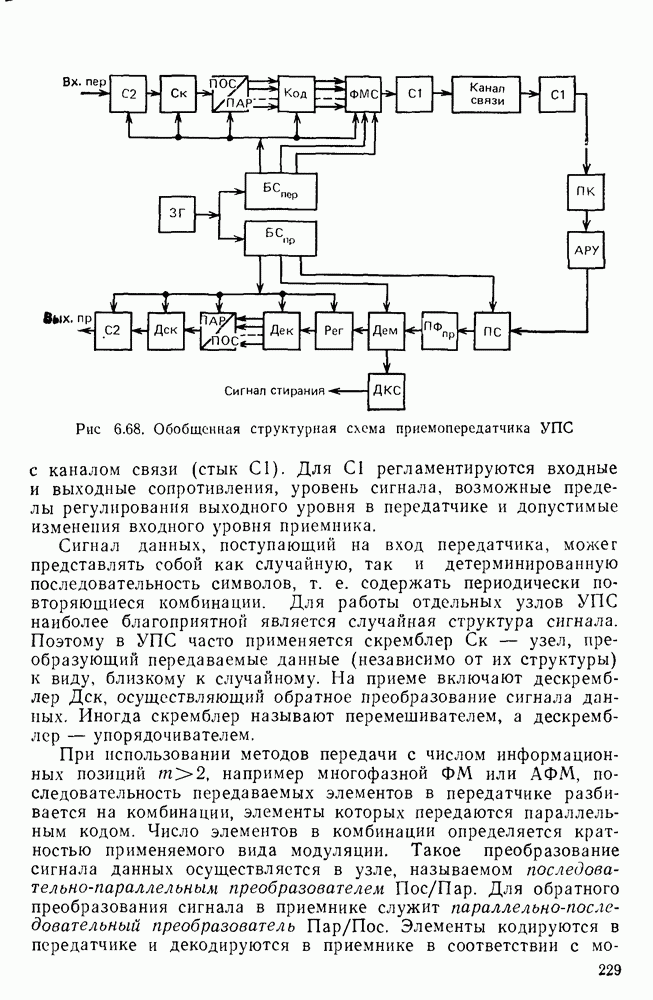
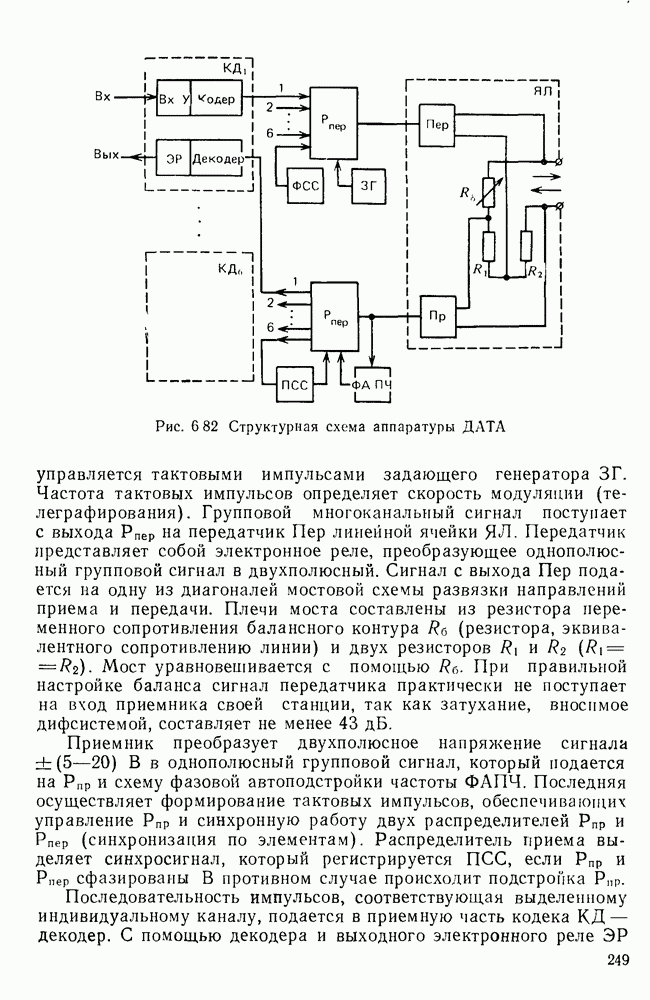
- 6.8. УСТРОЙСТВА ПРЕОБРАЗОВАНИЯ СИГНАЛОВ АПД
- Примеры УПС. Рекомендации МККТТ по построению УПС.
- Оценка качества прнимаемых сигналов в УПС.
- Разделение направлений передачи и приема.
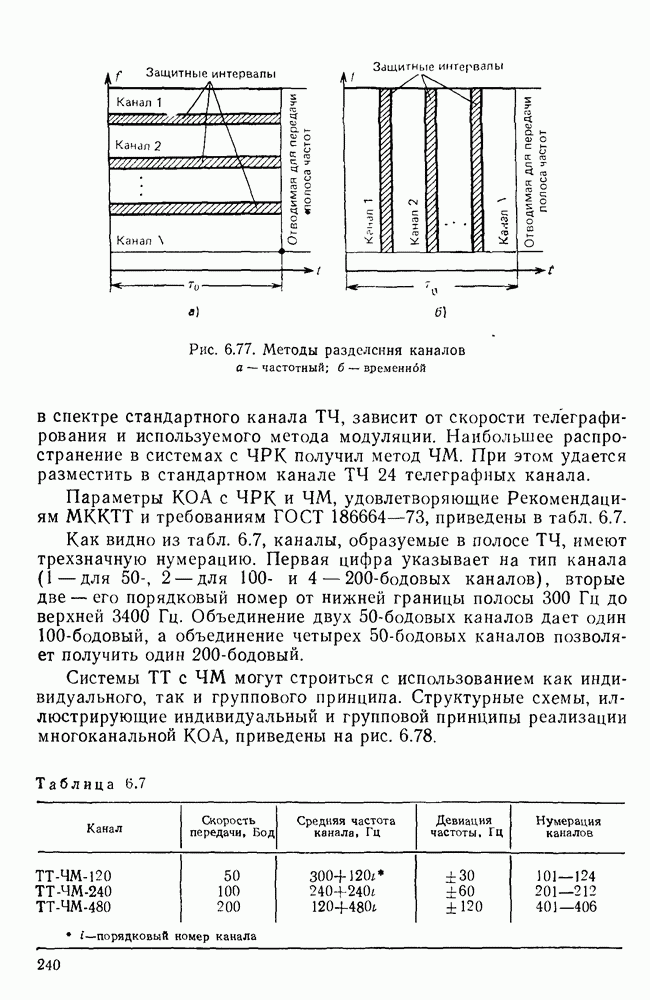
- 6.9. ТЕЛЕГРАФНАЯ КАНАЛООБРАЗУЮЩАЯ АППАРАТУРА
- Примеры телеграфной аппаратуры образования дискретных каналов.
- Каналообразующая аппаратура магистральных связей.
- Аппаратура зоновой связи.
- Аппаратура городских связей.
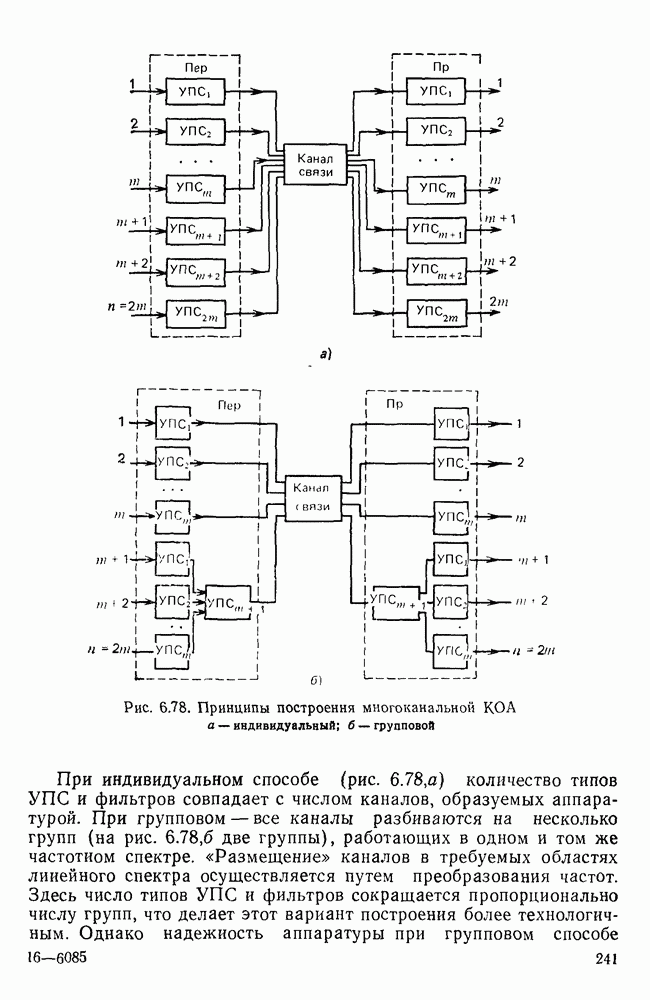
- Принципы построения универсального комплекса КОА.
- Устройства УТА и УНТА одноканальные
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 7. МЕТОДЫ ПОСТРОЕНИЯ И ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- 7.1. ЛИНЕЙНЫЕ КОДЫ
- Обнаружение и исправление ошибок. Декодирующее устройство.
- Примеры линейных кодов.
- 7.2. ЦИКЛИЧЕСКИЕ КОДЫ
- Базис циклического кода, формирование кодовых комбинаций.
- 7.3. СИНДРОМ ЦИКЛИЧЕСКОГО КОДА И ЕГО СВОЙСТВА
- Оптимальное декодирование на основе анализа веса.
- 7.4. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.5. ПОНЯТИЕ ОБ ИТЕРАТИВНЫХ И КАСКАДНЫХ КОДАХ [7.1]
- Каскадные коды.
- 7.6. ПОНЯТИЕ О НЕПРЕРЫВНЫХ КОДАХ
- Сверточные коды.
- 7.7. ПРИНЦИПЫ ТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ КОРРЕКТИРУЮЩИХ КОДОВ
- Построение кодирующего устройства циклического кода.
- Программная реализация помехоустойчивых кодов.
- 7.8. МЕТОДИКА ВЫБОРА КОРРЕКТИРУЮЩИХ КОДОВ
- Код (n, n-1) с защитой на четность.
- 7.9. СОПРЯЖЕНИЕ ПРОЦЕДУР ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ
- Прием по наиболее надежным символам.
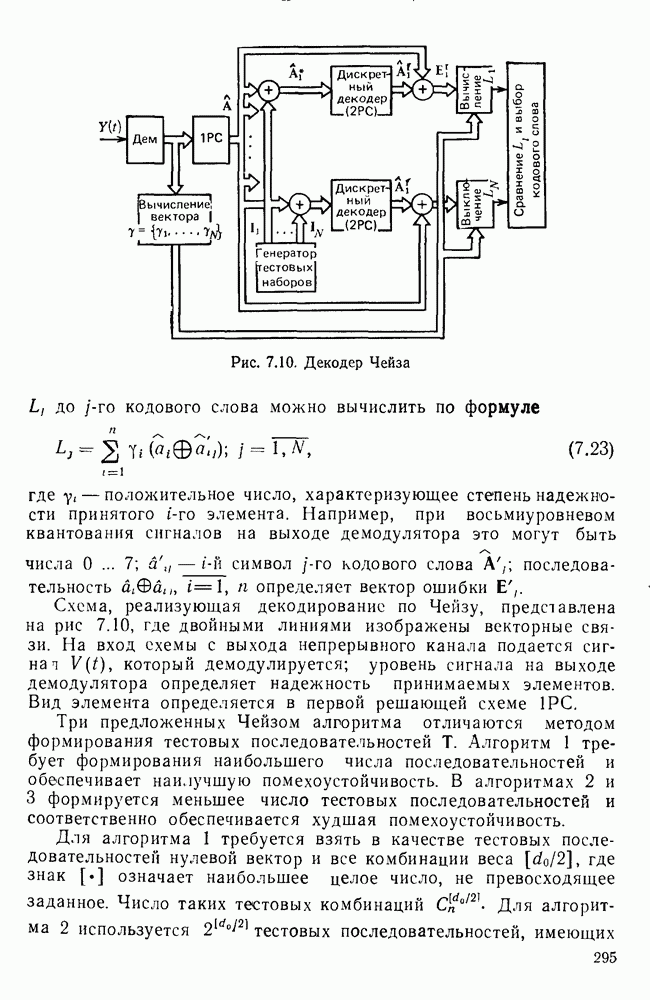
- Класс алгоритмов Чейза [7.2].
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Глава 8. АДАПТАЦИЯ В СИСТЕМАХ ПДС
- Контроль за состоянием канала связи.
- 8.2. КЛАССИФИКАЦИЯ СИСТЕМ С ОБРАТНОЙ СВЯЗЬЮ
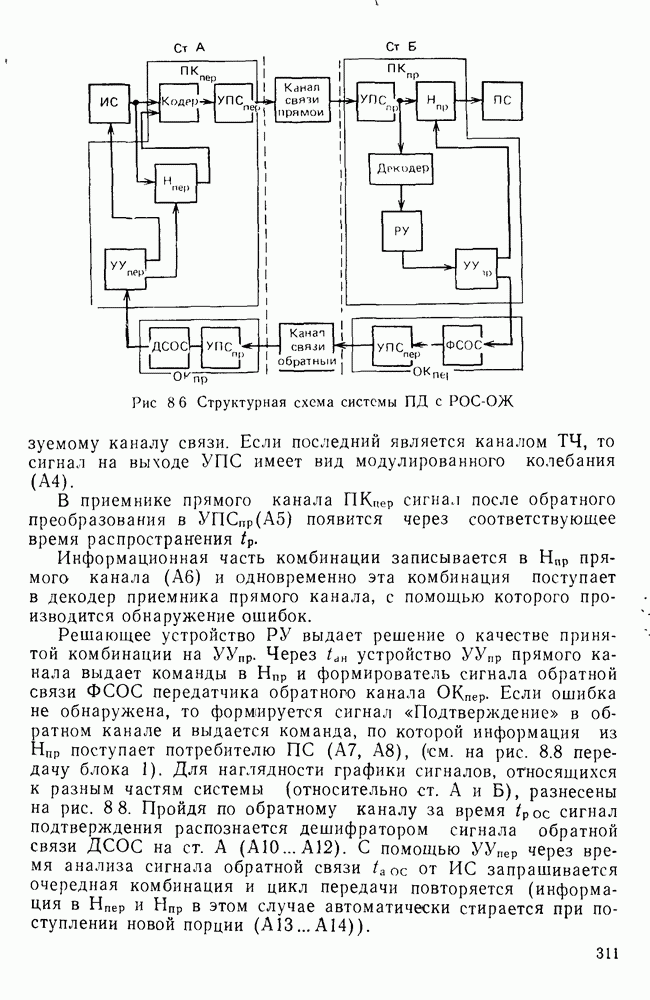
- 8.3. СТРУКТУРНЫЕ СХЕМЫ, АЛГОРИТМЫ И ХАРАКТЕРИСТИКИ НЕКОТОРЫХ СИСТЕМ С РОС И ИОС
- Система с РОС и непрерывной передачей информации и блокировкой РОС-НПбл.
- Система с РОС и адресным переспросом РОС-АП.
- Система с информационной обратной связью (ИОС).
- КОНТРОЛЬНЫЕ ВОПРОСЫ
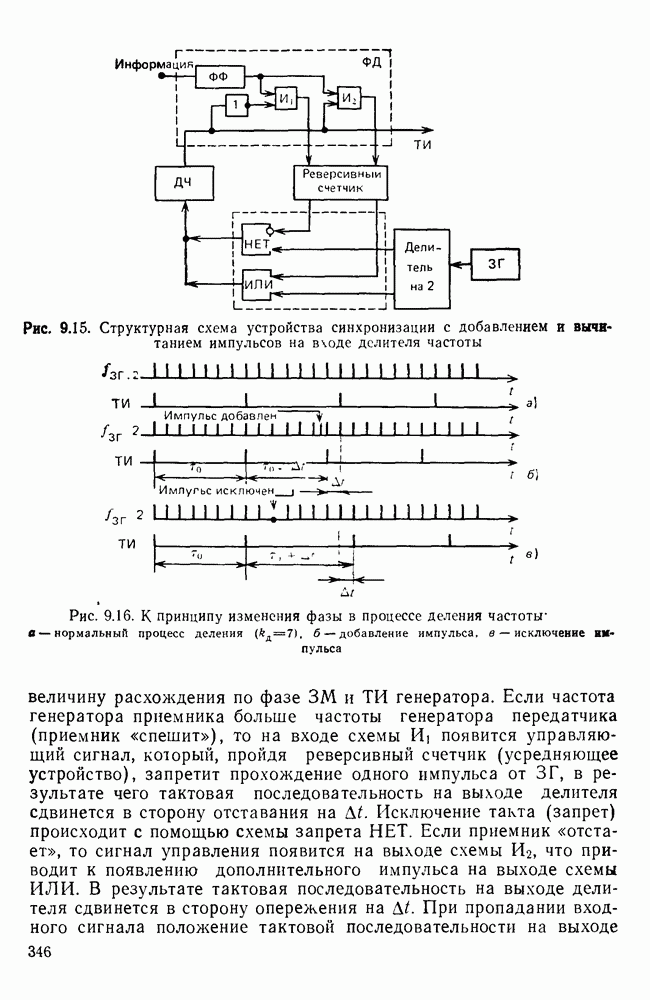
- Глава 9. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ В СИСТЕМАХ ПДС
- 9.1. СИНХРОНИЗАЦИЯ В СИНХРОННЫХ И СТАРТСТОПНЫХ СИСТЕМАХ ПДС
- Синхронизация в синхронных системах.
- Особенности поэлементной и групповой синхронизации при стартстопном методе передачи.
- 9.2. МЕТОДЫ И УСТРОЙСТВА СИНХРОНИЗАЦИИ ПО ЭЛЕМЕНТАМ
- 9.3. МЕТОДЫ И УСТРОЙСТВА ГРУППОВОЙ И ЦИКЛОВОЙ СИНХРОНИЗАЦИИ
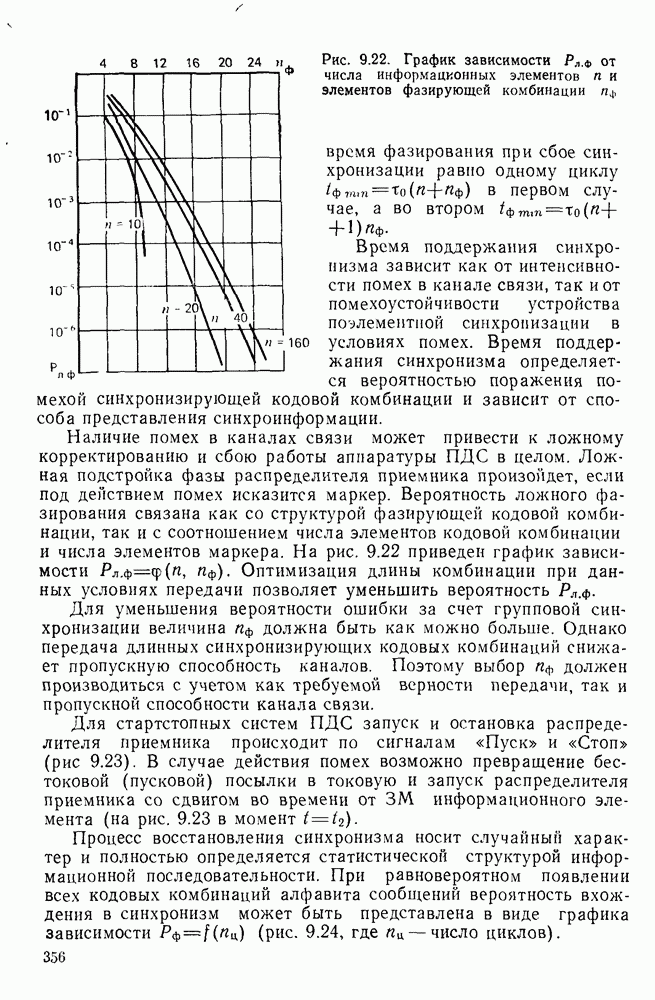
- 9.4. РАСЧЕТ ПАРАМЕТРОВ УСТРОЙСТВ СИНХРОНИЗАЦИИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
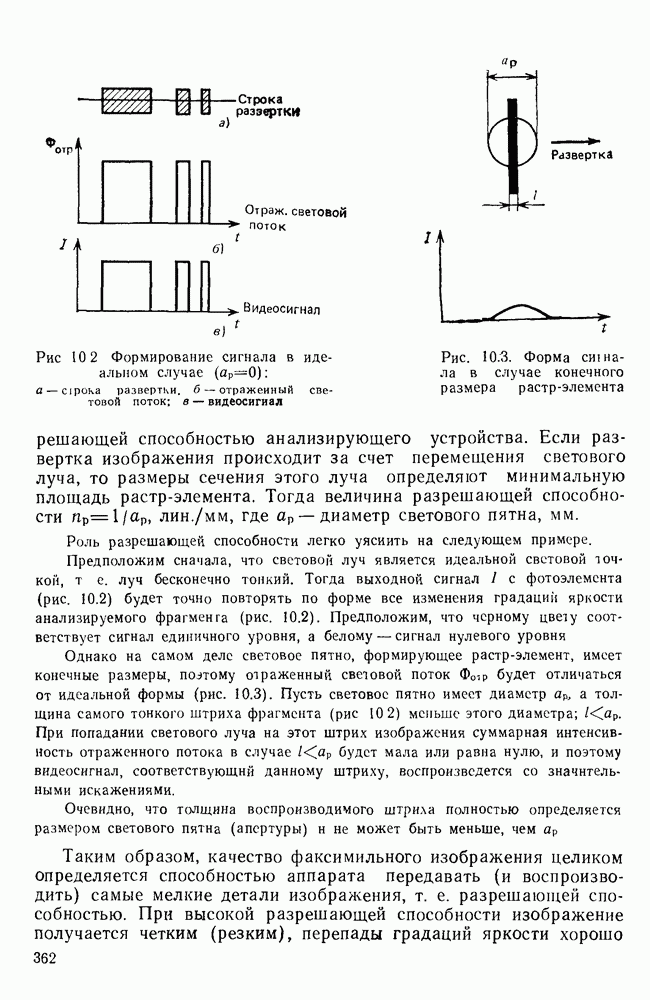
- Глава 10. СИСТЕМЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИИ
- 10.1. ПРИНЦИПЫ ФАКСИМИЛЬНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ
- 10.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ФАКСИМИЛЬНЫХ СИСТЕМ СВЯЗИ
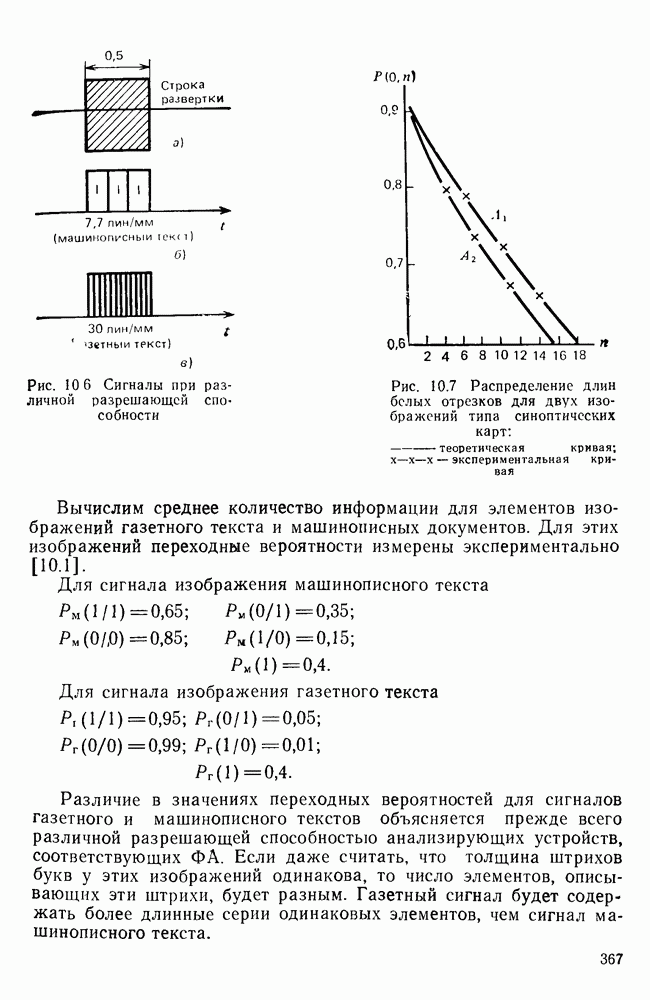
- 10.3. КВАНТОВАНИЕ И ДИСКРЕТИЗАЦИЯ ВИДЕОСИГНАЛА
- 10.4. МОДЕЛИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.5. ЭФФЕКТИВНЫЕ МЕТОДЫ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СООБЩЕНИЙ
- 10.6. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ФАКСИМИЛЬНЫХ СИГНАЛОВ
- 10.7. ОСОБЕННОСТИ АНАЛИЗА И СИНТЕЗА ИЗОБРАЖЕНИЙ
- 10.8. СОВРЕМЕННАЯ ЦИФРОВАЯ ФАКСИМИЛЬНАЯ АППАРАТУРА
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ИССЛЕДОВАНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПДС МЕТОДОМ ИМИТАЦИОННОГО (СТАТИСТИЧЕСКОГО) МОДЕЛИРОВАНИЯ
- П. 1.2. МОДЕЛИРОВАНИЕ ОТДЕЛЬНЫХ БЛОКОВ СИСТЕМЫ ПДС
- П. 1.3. МАТРИЧНАЯ МОДЕЛЬ СИСТЕМЫ ПДС
- Приложение 2. ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ В ДОКУМЕНТАЛЬНОЙ ЭЛЕКТРОСВЯЗИ
- П. 2.2 ОСОБЕННОСТИ ВЫБОРА И ИСПОЛЬЗОВАНИЯ МПС ДЛЯ СИСТЕМ ПДС
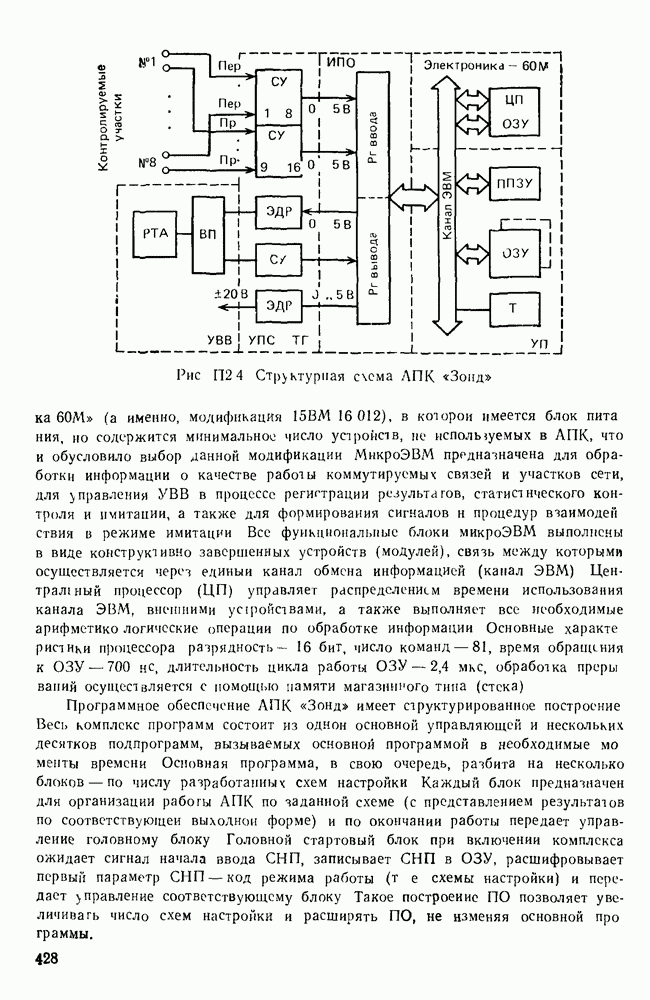
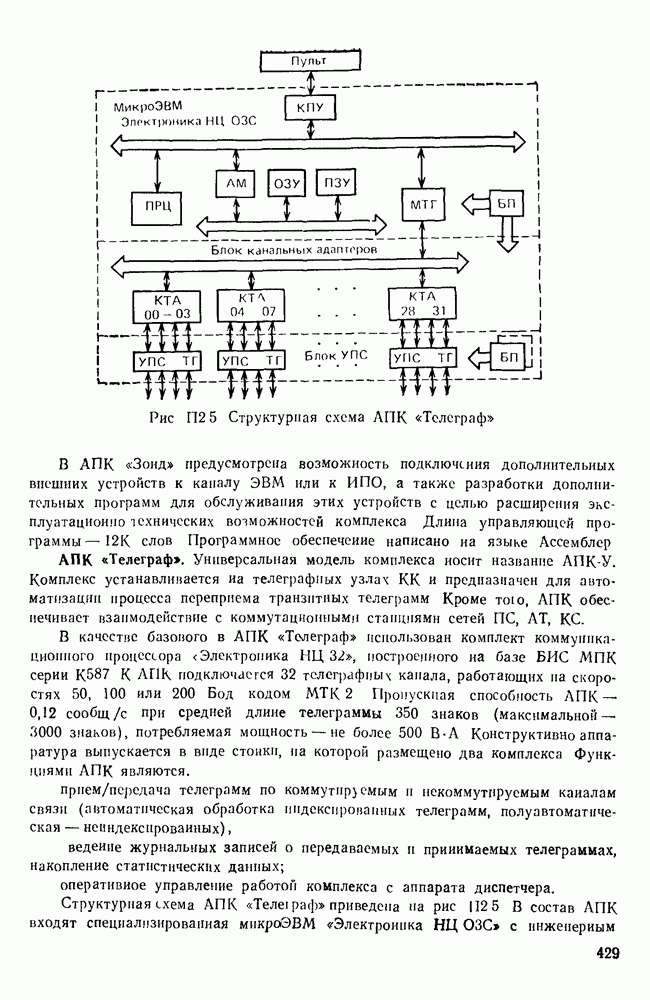
- П. 2.3. ПРИМЕРЫ РЕАЛИЗАЦИИ СИСТЕМ ПДС НА ОСНОВЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
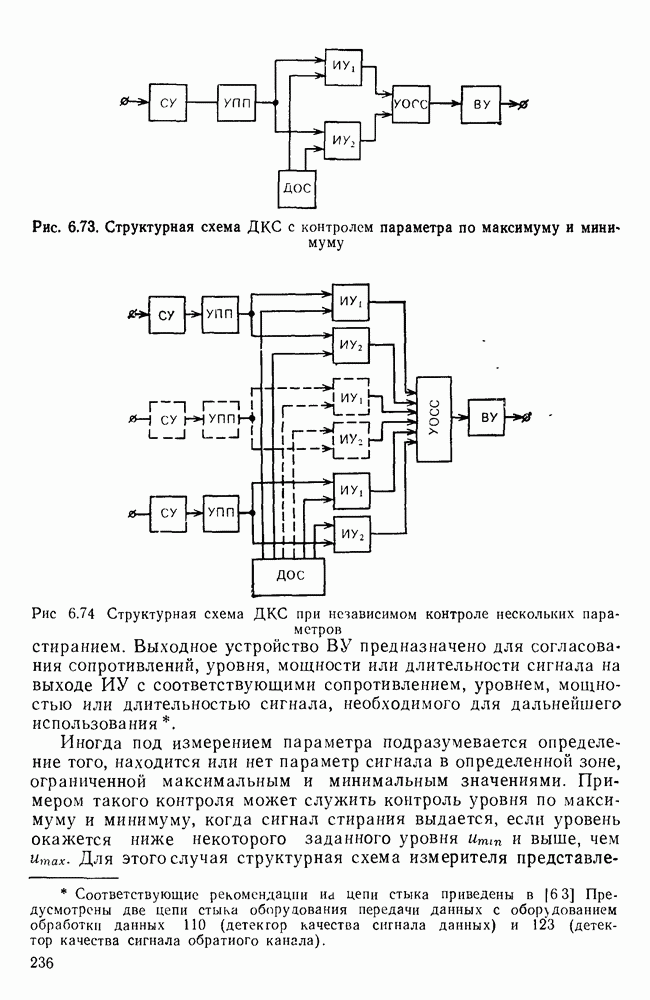
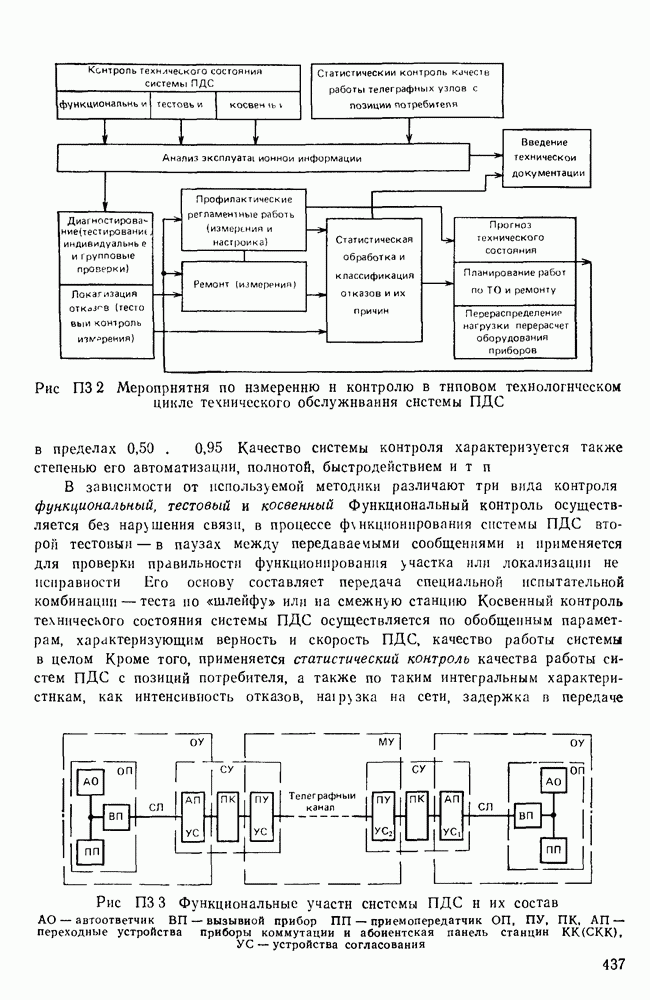
- Приложение 3. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СЕТЯХ И СИСТЕМАХ ПДС
- П. 3.1. МЕТОДЫ УЛУЧШЕНИЯ ЭКСПЛУАТАЦИОННО-ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК СЕТЕЙ И СИСТЕМ ПДС
- П. 3.2. ЦЕЛИ И ЗАДАЧИ СИСТЕМЫ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.3 СИСТЕМЫ И СЕТИ ПДС КАК ОБЪЕКТ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.4. ТЕХНИЧЕСКИЕ СРЕДСТВА СИСТЕМ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.5 АВТОМАТИЗАЦИЯ КОНТРОЛЯ И ИЗМЕРЕНИЙ
- П. 3.6. ИСПОЛЬЗОВАНИЕ ДОСТИЖЕНИЙ МИКРОЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ
- П 3.7 ОСНОВНЫЕ ТЕНДЕНЦИИ В РАЗВИТИИ СКИ
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- СПИСОК ЛИТЕРАТУРЫ