| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
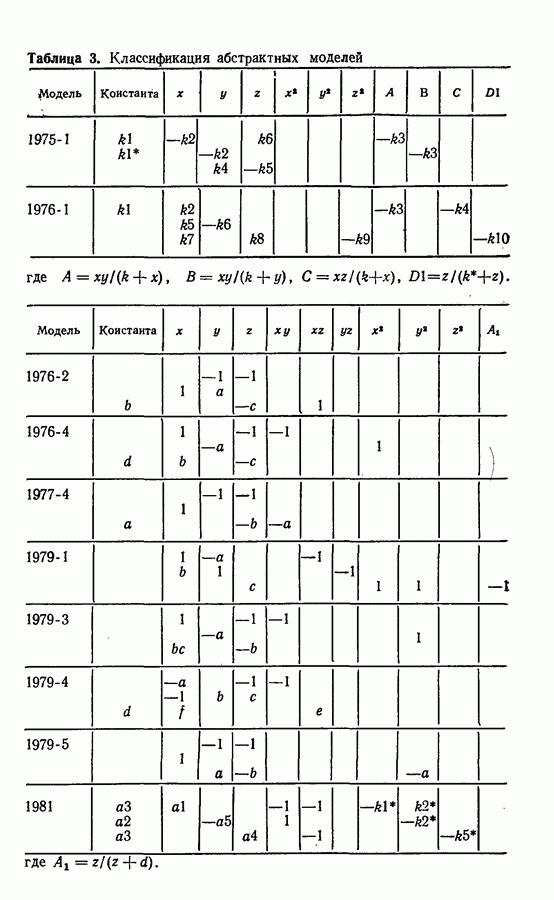
3.9. Бимолекулярная модель
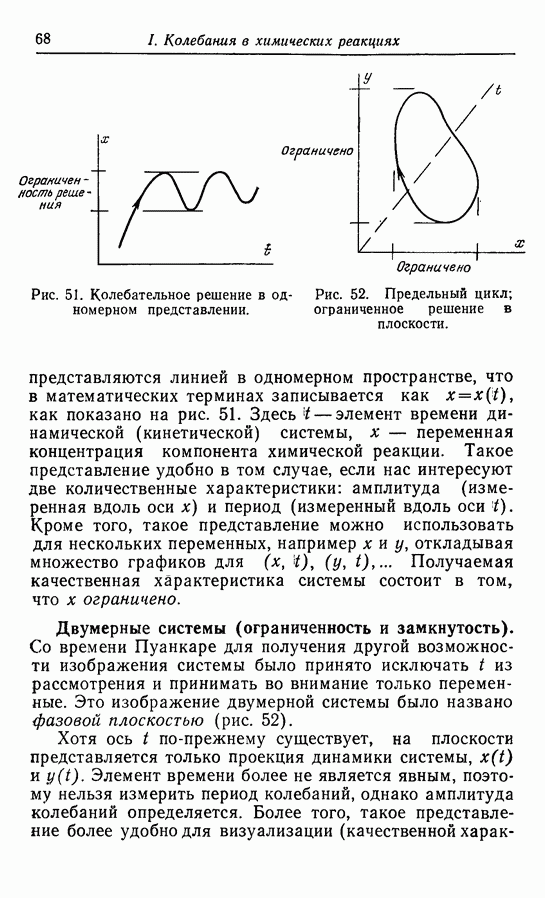
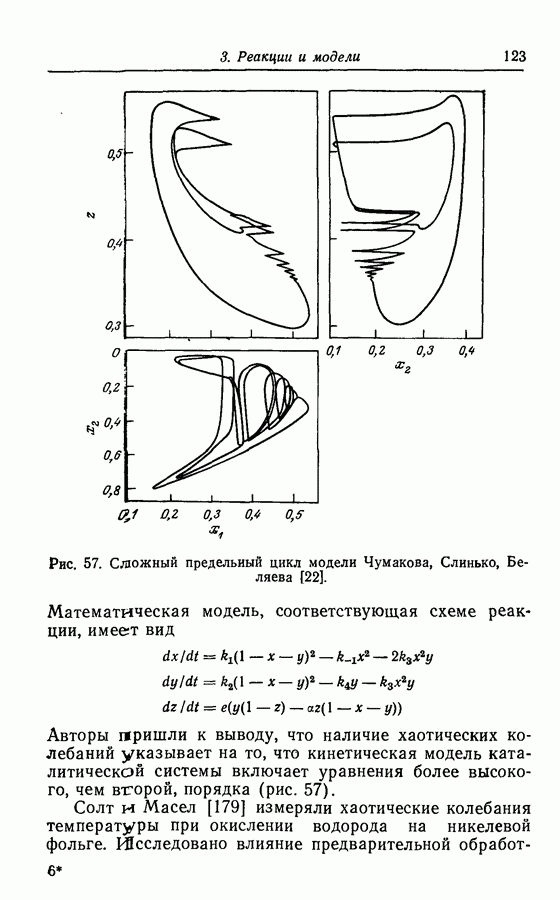
В 1968 г. Лефевром [66] была предложена гипотетическая модель, основанная на бимолекулярной реакции. Эта модель для некоторых значений параметров имеет периодическое решение, представляющее собой предельный цикл.
Схема реакции. Схема реакции состоит из следующего набора реакций, включающих два промежуточных компонента (X и Y) [66]:

Дифференциальные уравнения. Кинетические уравнения представляют собой два нелинейных дифференциальных уравнения относительно концентраций X и Y; нелинейность здесь представлена простыми степенными величинами, такими, как

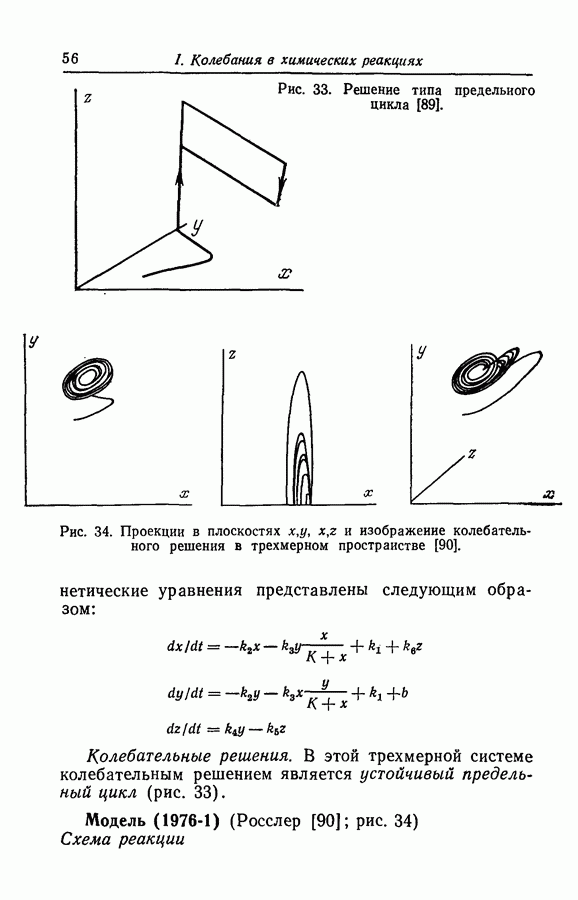
Решения математической модели. Эта модель обладает единственной особой точкой, которая в результате

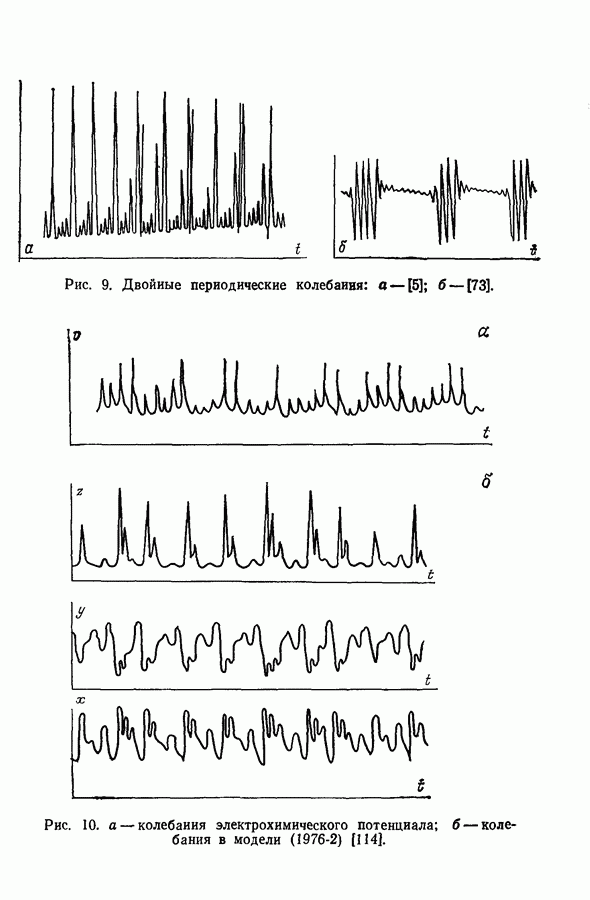
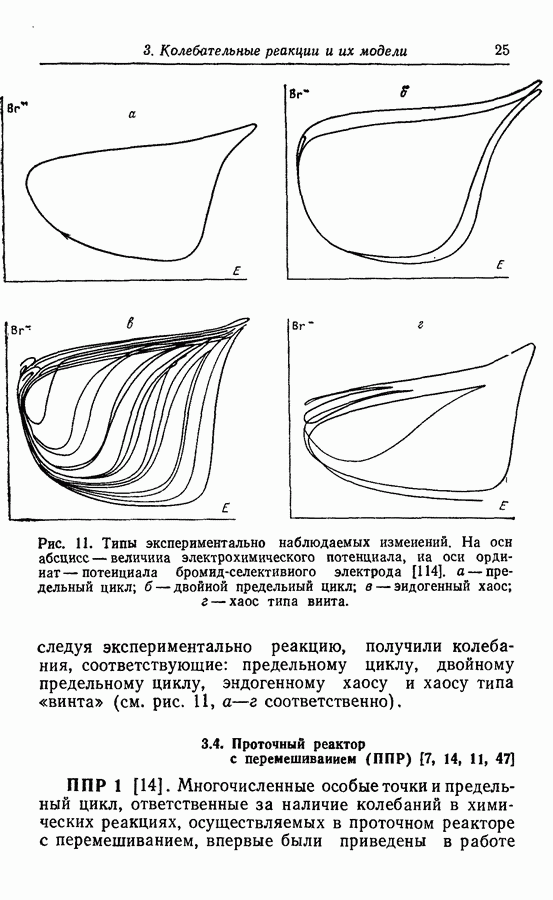
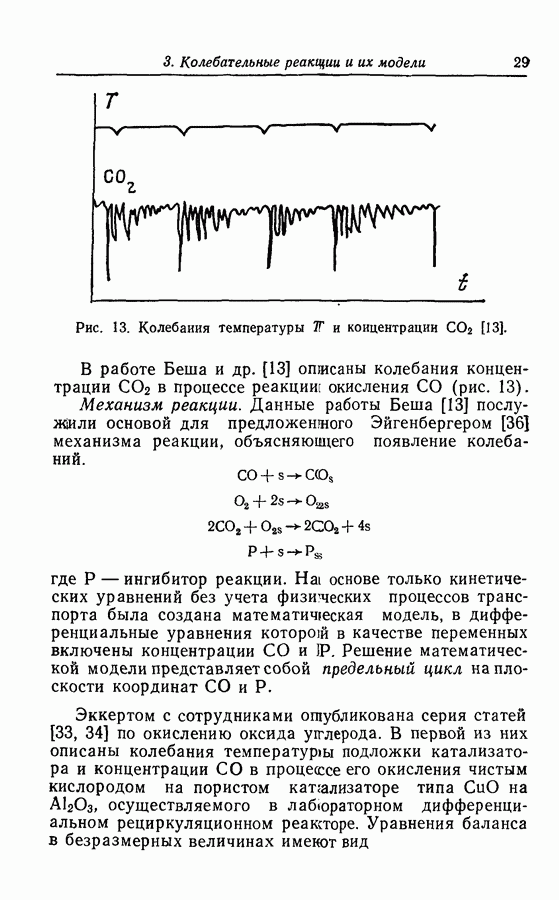
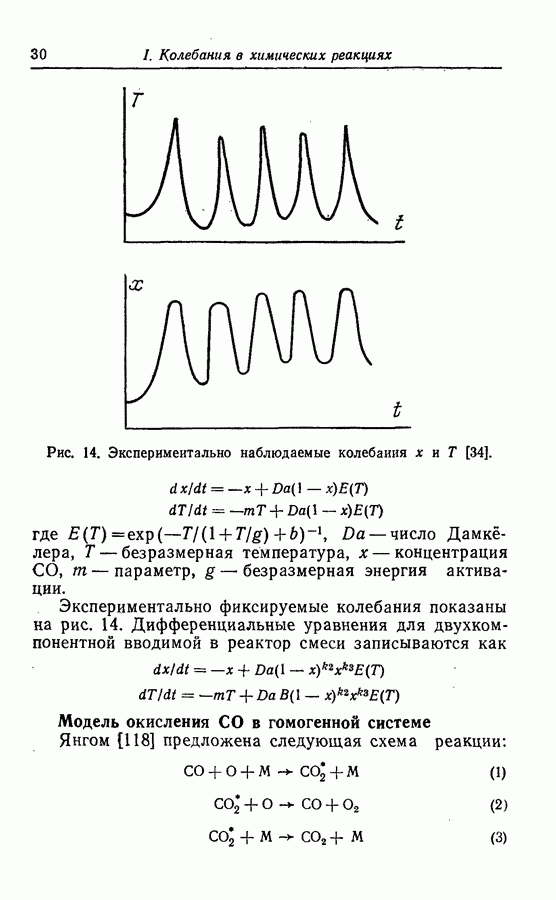
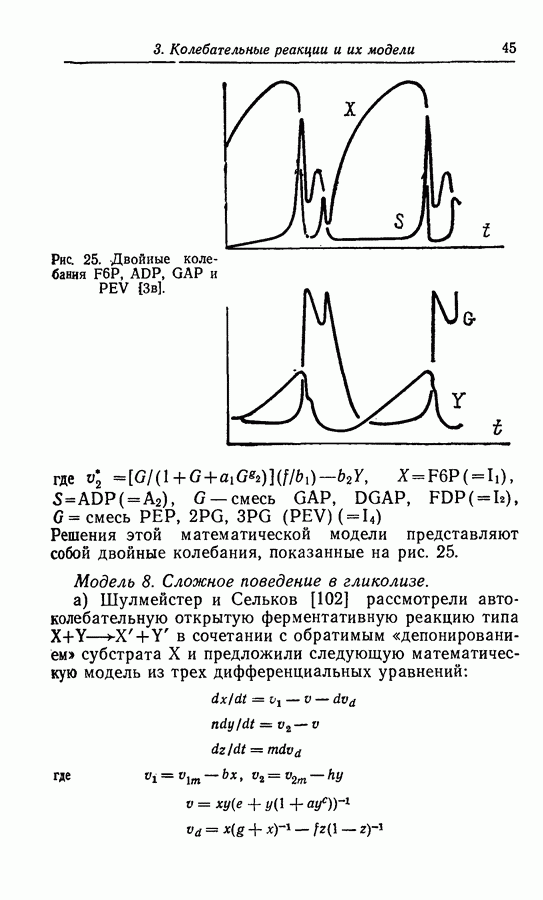
Рис. 32. Предельный цикл модели брюсселятора [67].
бифуркации затем переходит в неустойчивую особую точку и окружающий ее устойчивый предельный цикл (рис. 32) [67].
Бифуркационный анализ. Так как дифференциальный уравнения достаточно просты, они могут быть непосредственно использованы в бифуркационном анализе. Единственная особая точка системы при  соответствует значениям
соответствует значениям 
Матрица коэффициентов для линеаризованных уравнений при  имеет вид
имеет вид

Три условия Пуанкаре, как показано в работе Гарела [53], могут быть сформулированы следующим образом:
1. Детерминант матрицы коэффициентов становится равным нулю,  и, следовательно, это условие выполняется при
и, следовательно, это условие выполняется при 
2. Изменение устойчивости соответствует характеристическому уравнению  решение которого дает
решение которого дает  .
.
 при
при  т. е. при значениях параметров
т. е. при значениях параметров 
3. В действительности два решения, соответствующие особой точке  подвергаются бифуркации; новое решение представляет собой устойчивый предельный цикл. Для точки с величинами параметров
подвергаются бифуркации; новое решение представляет собой устойчивый предельный цикл. Для точки с величинами параметров  лежащей в плоскости параметров, Лефевр и Николис [67] получили решения, соответствующие предельному циклу и неустойчивой особой точке одновременно.
лежащей в плоскости параметров, Лефевр и Николис [67] получили решения, соответствующие предельному циклу и неустойчивой особой точке одновременно.

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. КОЛЕБАНИЯ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 3. Колебательные реакции и их модели
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
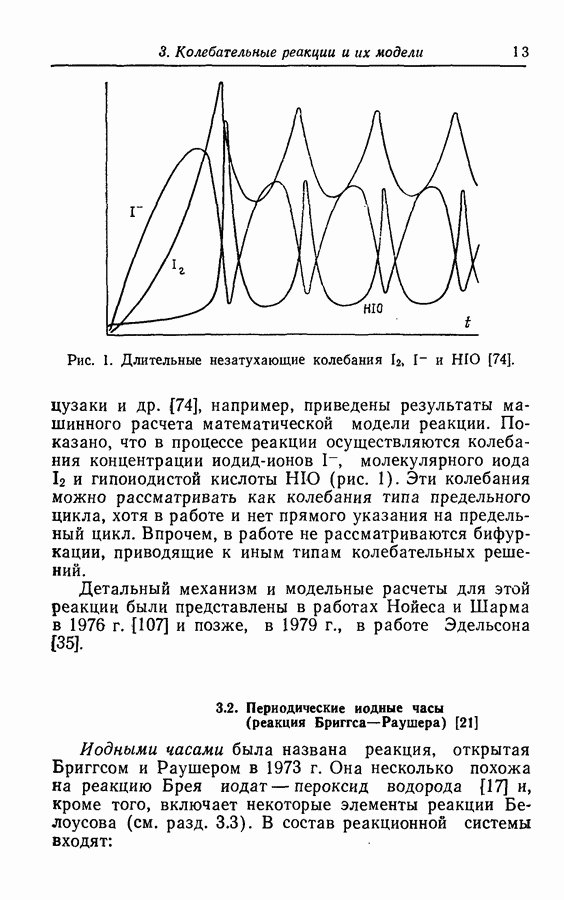
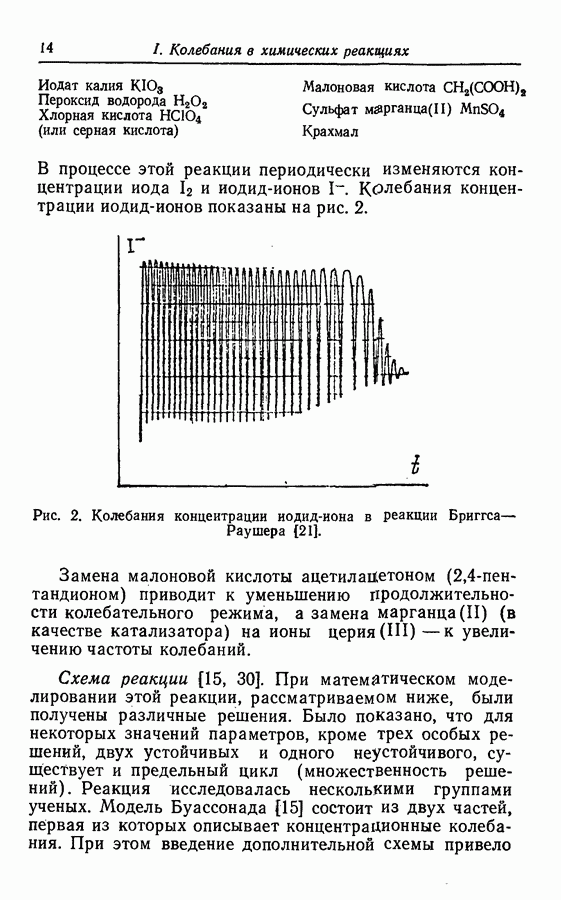
- 3.2. Периодические водные часы (реакция Бриггса—Раушера) [21]
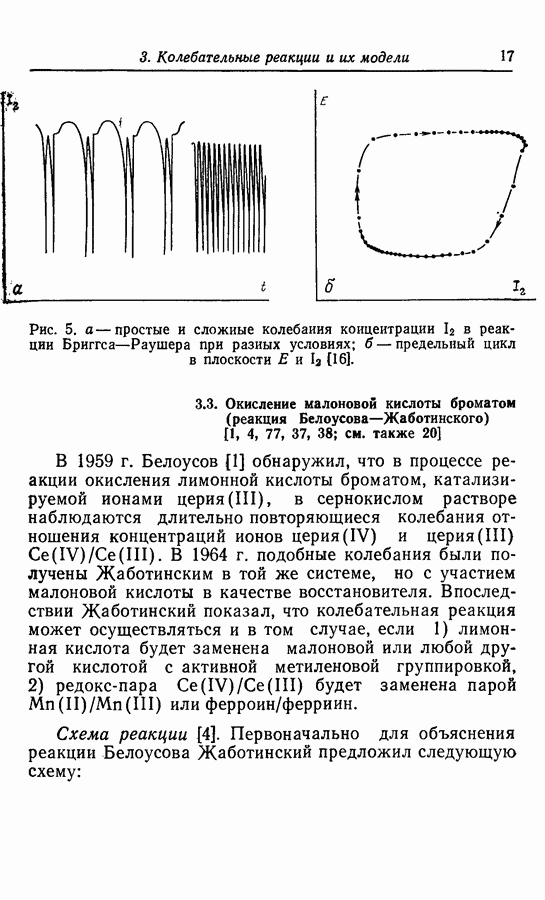
- 3.3. Окисление малоновоб кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием (ППР) [7, 14, II, 47]
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций и их модели
- 3.11. Некаталитические реакции
- 3.12. Таблица колебательных реакций
- 4. Характеристики колебательных систем
- 4.2. Нелинейность систем
- 4.3. Параметры системы
- 4.4. Число решений
- 5. Глобальный анализ
- 5.2. Бифуркации как способ поиска колебаний
- 6. Классификация колебаний
- 6.2. Типы компонентов колебательных химических реакций
- 6.3. Типы колебательных математических решений
- 7. Состояние исследований и дальнейшие направления их развития
- Часть II. РАЗВИТИЕ ИССЛЕДОВАНИЙ ХИМИЧЕСКИХ КОЛЕБАНИЙ В ПОСЛЕДНЕЕ ВРЕМЯ
- 3. Реакции и модели, проявляющие колебания
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Колебательные йодные часы (реакция Бриггса—Раушера)
- 3.3. Окисление малоновой кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций
- 3.11. Некаталитические реакции
- 3.12. Окисление хлоритом
- 3.13. Разноплановые исследования
- 3.14. Общие модели и математические методы