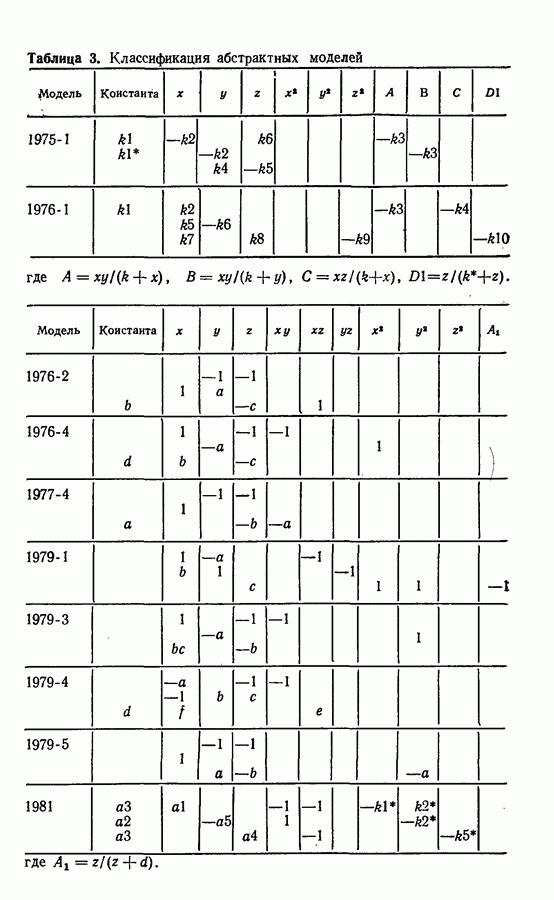
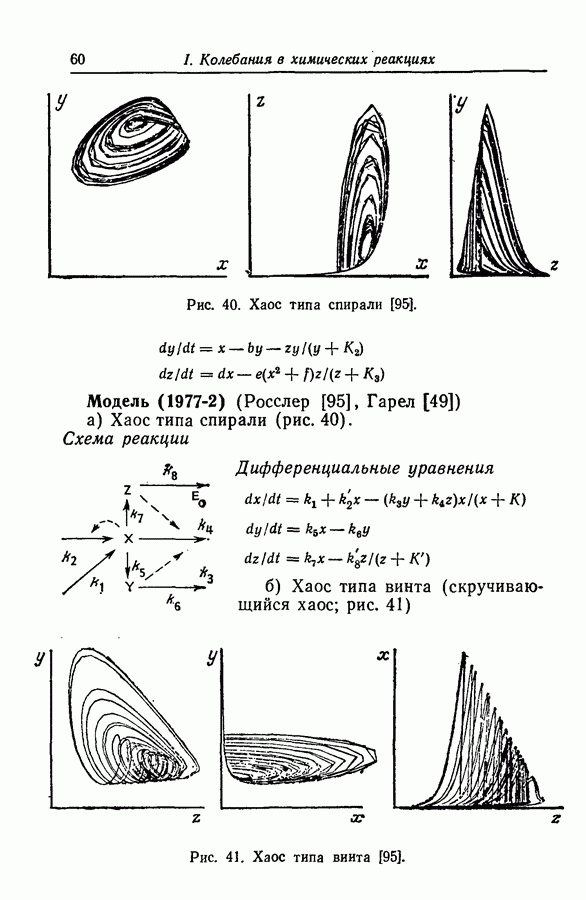
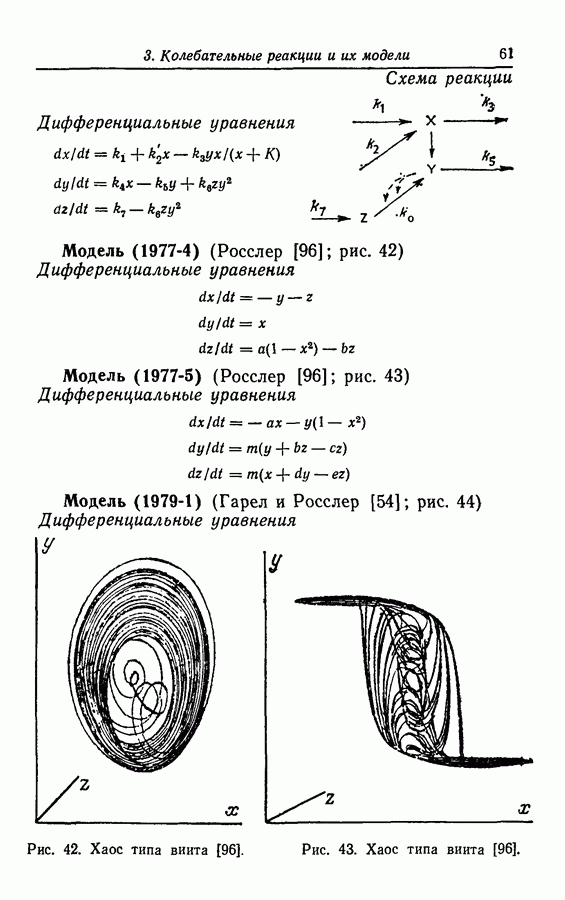
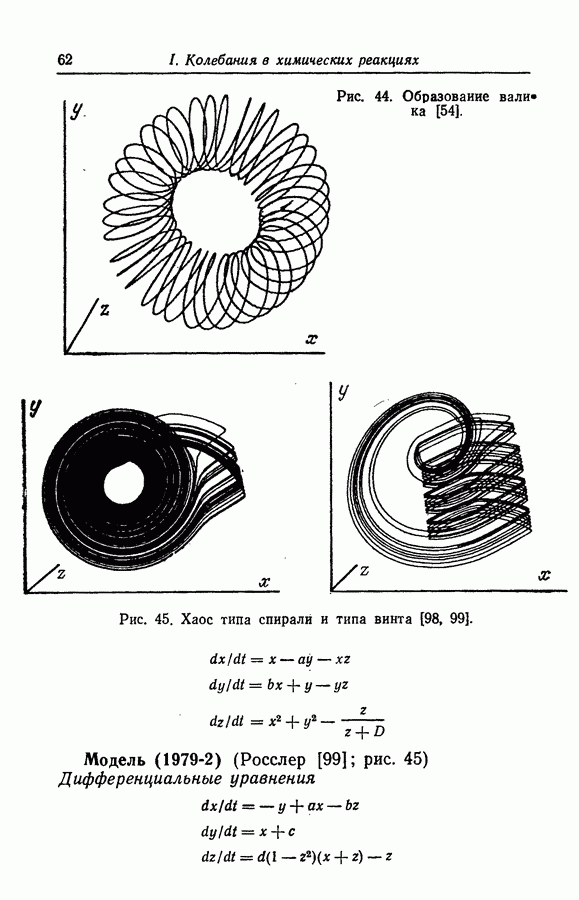
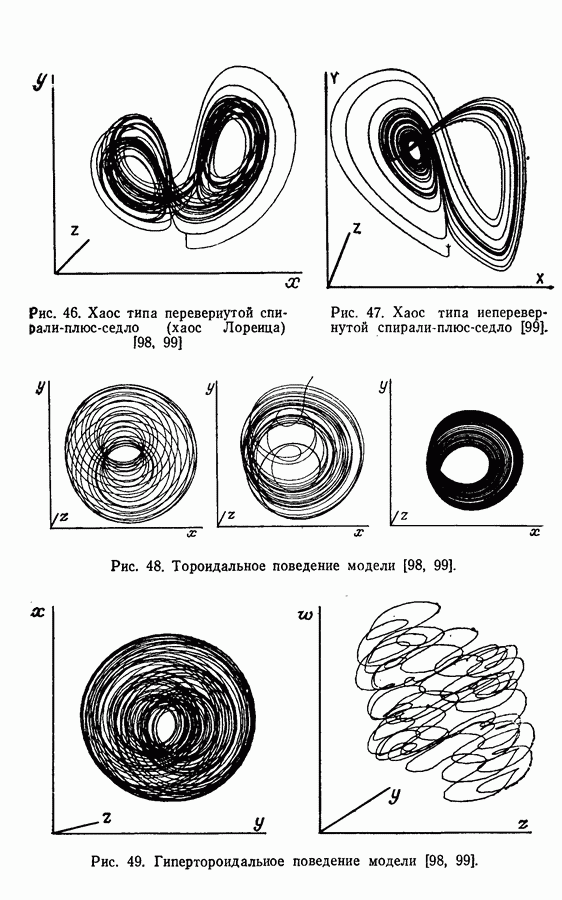
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.6. Колебания в гликолизе
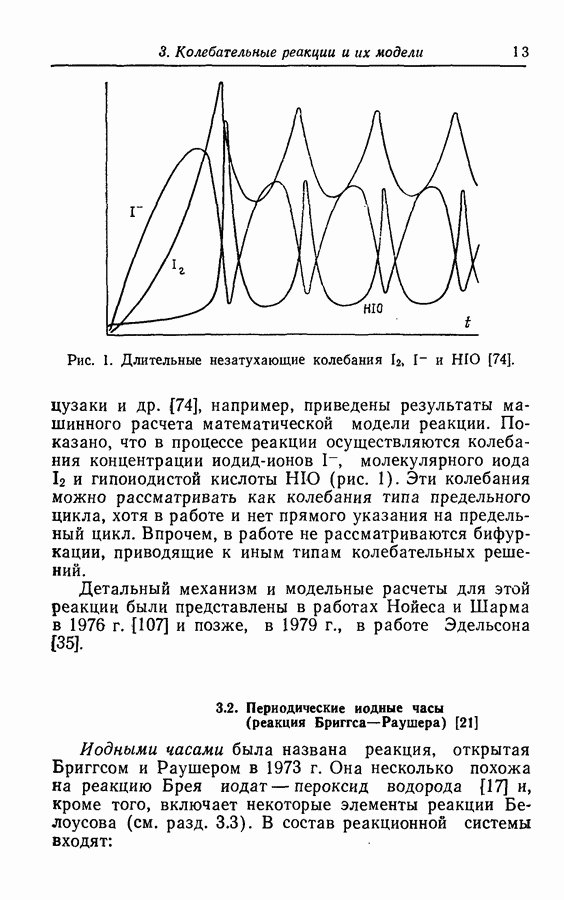
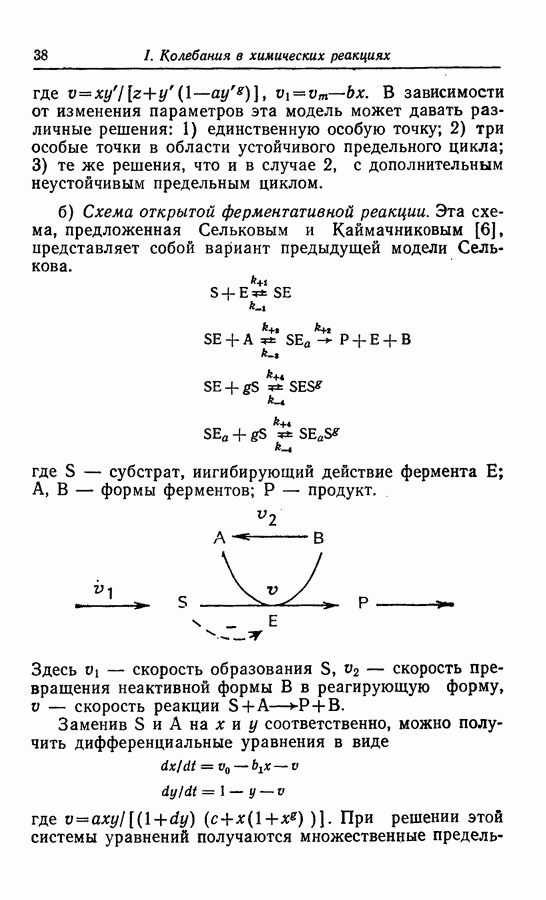
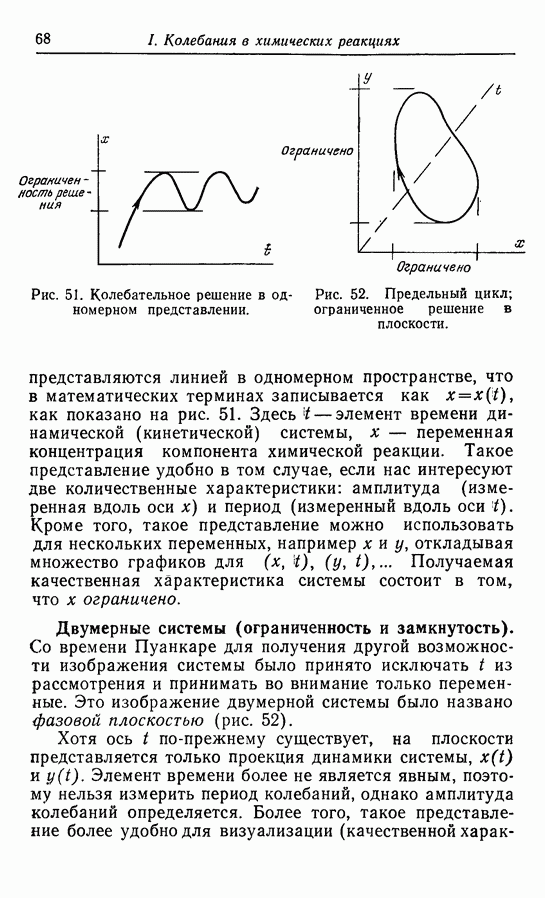
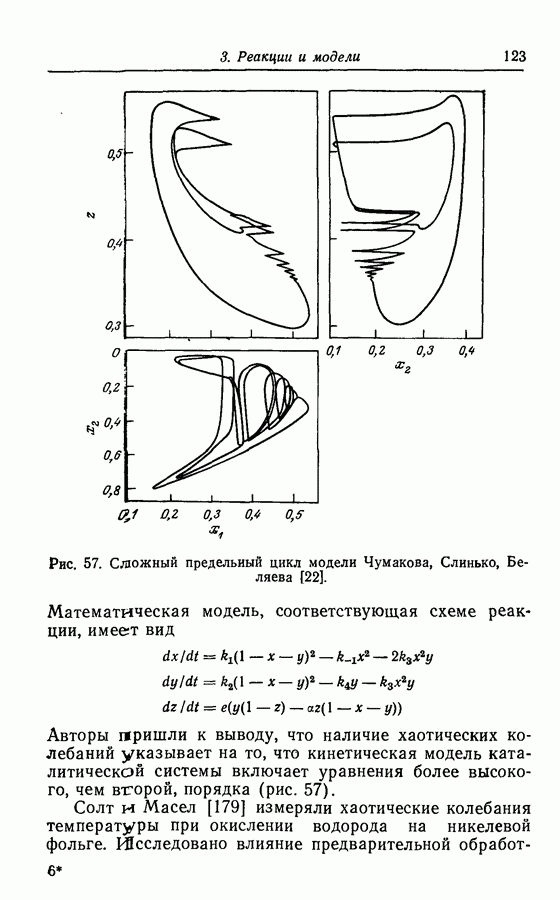
Колебания в гликолитической системе наблюдались многочисленными исследователями, наиболее ранней (1957 г.) является работа Дайсенса и Амеца [32]. Было найдено, что при добавлении глюкозы (GLU) в гликолитической системе возникают колебания концентрации восстановленного фосфопиридинового нуклеотида (NADH). Подобные колебания концентрации NADH в клеточном экстракте были обнаружены позднее Чансом и др. [23], а затем Гош и Чанс [41] описали в той же системе колебания концентраций фруктозо-1,6-дифосфата FDP и глюкозо-6-фосфата  (рис. 18).
(рис. 18).

Рис. 18. Колебания концентраций FDP и G6P [41].
Механизм реакции. Общий химический механизм, используемый для объяснения гликолитических колебаний, был сформулирован Хиггинсом [56] на основе уже известной химии фосфофруктокиназы и связанных с нею гликолитических интермедиатов:

где  — фосфофруктокиназа (фермент);
— фосфофруктокиназа (фермент);  (субстрат);
(субстрат);  (продукт);
(продукт);  — смесь альдолазы и изомеразы триазофосфата (фермент); GAP — глицеральдегидфосфат (продукт). Этот же механизм может быть записан в общем виде как
— смесь альдолазы и изомеразы триазофосфата (фермент); GAP — глицеральдегидфосфат (продукт). Этот же механизм может быть записан в общем виде как

Колебания типа предельного цикла в основном относятся к колебаниям концентрации пары  Кроме того, периодически меняется концентрация глюкозы, превращающейся в
Кроме того, периодически меняется концентрация глюкозы, превращающейся в  на первой стадии по реакции первого порядка. На второй стадии активированная форма фосфофруктокиназы действует как фермент, а
на первой стадии по реакции первого порядка. На второй стадии активированная форма фосфофруктокиназы действует как фермент, а  проявляет на этой стадии активирующее действие. Конечным продуктом реакции является глицеральдегидфосфат
проявляет на этой стадии активирующее действие. Конечным продуктом реакции является глицеральдегидфосфат 
Модели колебательных реакций в гликолизе
Модель 1. Модель обратной активации. В 1967 г. Хиггинс  предложил несколько моделей для гликолитической системы, основанные на механизмах обратной
предложил несколько моделей для гликолитической системы, основанные на механизмах обратной
связи по типу обратной активации, обратного ингибирования, прямой активации и прямого ингибирования. Мы рассмотрим здесь модель, в основе которой лежит механизм обратной связи по типу обратного активирования. В этом случае реакция может быть представлена уравнениями

где 
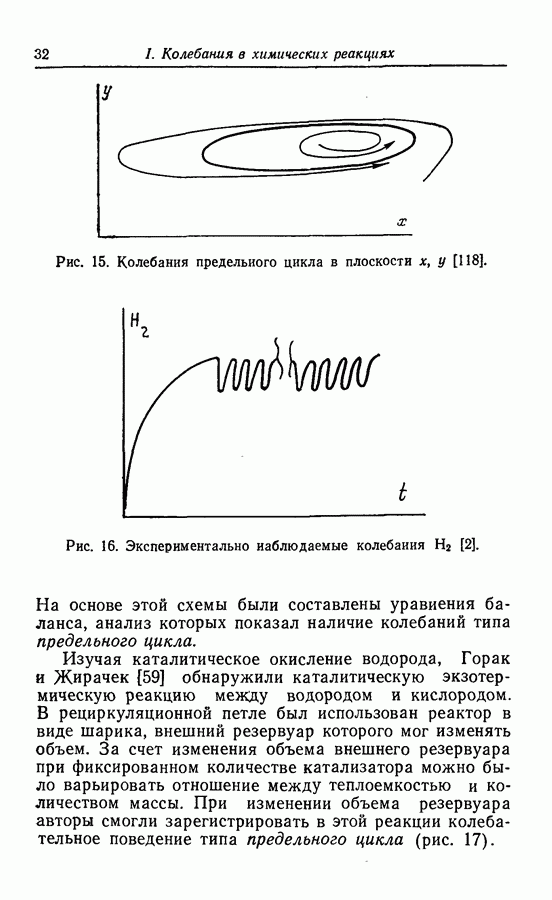
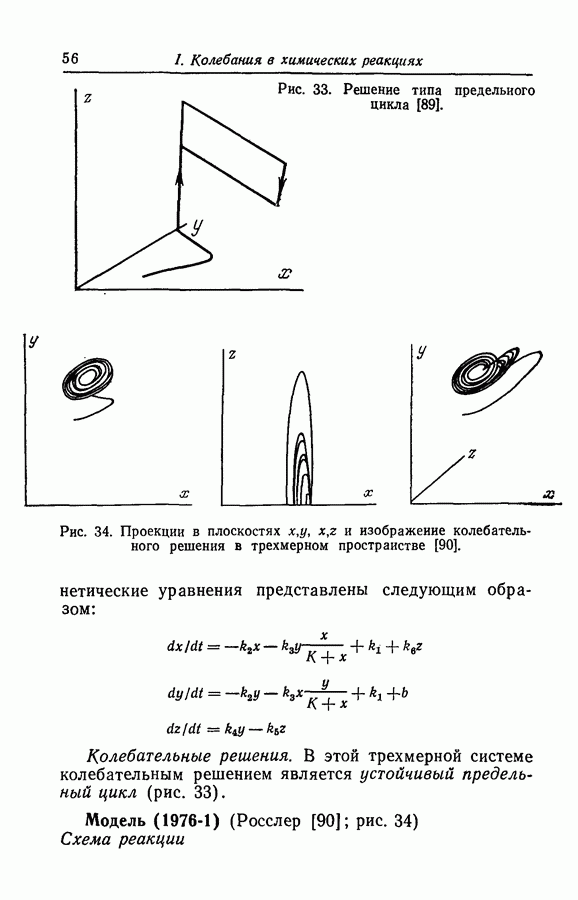
Решением этой модели является устойчивая особая точка, в которой проявляются бифуркации, приводящие к появлению устойчивого предельного цикла.
Модель 2. Предложенная Сельковым [103] модель гликолитической системы основана на превращениях фосфофруктокиназы:

где  — это ATP, поставляемый со скоростью
— это ATP, поставляемый со скоростью  и необратимо превращающийся в
и необратимо превращающийся в  — это ADP, продукт, который выводится со скоростью
— это ADP, продукт, который выводится со скоростью  -(неактивный) свободный фермент фосфофруктокиназа PFK. Е становится активным в сочетании с несколькими молекулами продукта,
-(неактивный) свободный фермент фосфофруктокиназа PFK. Е становится активным в сочетании с несколькими молекулами продукта,  образуя комплекс
образуя комплекс  степень активации PFK гликолитическими интермедиатами ADP и АМР.
степень активации PFK гликолитическими интермедиатами ADP и АМР.
Если обозначить  можно получить следующие дифференциальные уравнения:
можно получить следующие дифференциальные уравнения:


Учитывая, что пределы изменений последних трех производных малы, модель можно упростить, сведя ее от пяти к двум уравнениям. Произведя замену

получаем новые дифференциальные уравнения:

Если скорость гликолитических изменений очень мала  эти уравнения еще более упрощаются:
эти уравнения еще более упрощаются:

и для некоторых значений параметров модель соответствует устойчивому предельному циклу (рис. 19).

Рис. 19. Предельный цикл модели Селькова [103].
Модель 3. Предыдущая математическая модель гли-колитической системы в 1968 г. была проанализирована и проверена Сельковым [9], в результате чего им была создана новая модель:

где 
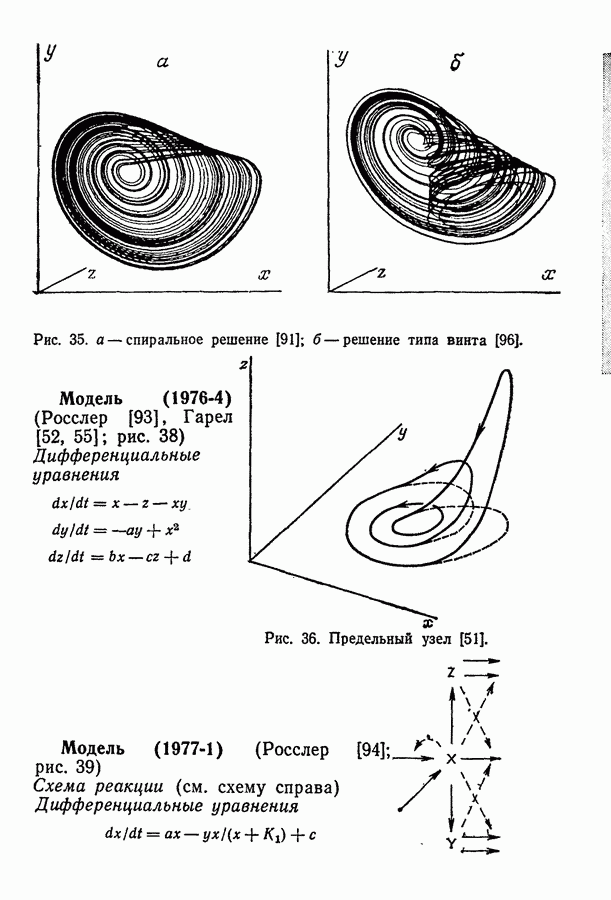
Несколько измененный в 1973 г. Сельковым совместно с Бетцем [105] вариант этой модели по-прежнему дает решение в виде только одной устойчивой особой точки и устойчивый предельный цикл, соответствующий колебательному характеру реакции.
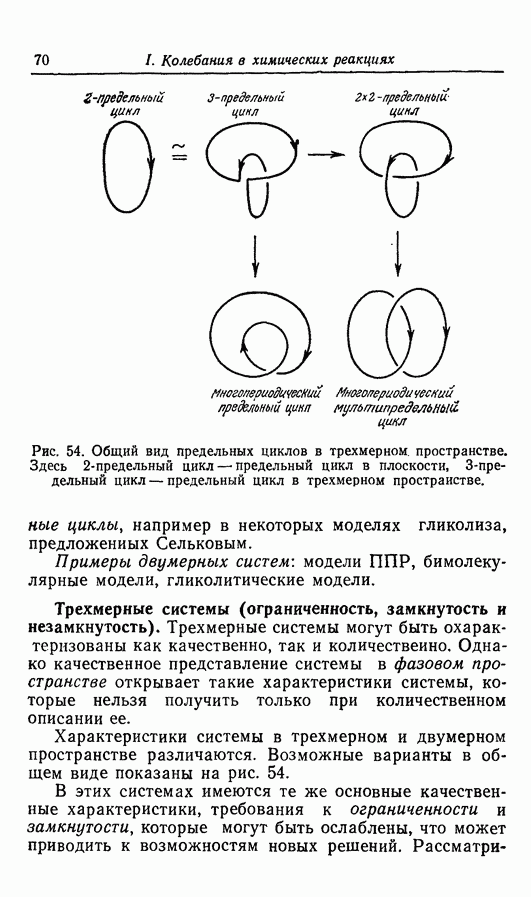
Тогда как в ранних моделях Селькова существует единственный предельный цикл, более поздние его модели имеют множественность решений как колебательных, так и неколебательных. И эти последние математические модели чрезвычайно интересны, так как это самые ранние модели биохимических колебаний, которые четко показывают наличие решений более сложных, чем простой предельный цикл. Такие решения характерны для большинства химических колебательных реакций, за исключением систем в моделях ППР.
Модель 4. Множественные особые точки и множественные предельные циклы.
а) Одна из ранних моделей Селькова [104] основана на реакции  катализируемой ферментом Е, действие которого в свою очередь ингибируется активной формой кофермента
катализируемой ферментом Е, действие которого в свою очередь ингибируется активной формой кофермента 

Схеме соответствуют дифференциальные уравнения

где  . В зависимости от изменения параметров эта модель может давать различные решения: 1) единственную особую точку; 2) три особые точки в области устойчивого предельного цикла; 3) те же решения, что и в случае 2, с дополнительным неустойчивым предельным циклом.
. В зависимости от изменения параметров эта модель может давать различные решения: 1) единственную особую точку; 2) три особые точки в области устойчивого предельного цикла; 3) те же решения, что и в случае 2, с дополнительным неустойчивым предельным циклом.
б) Схема открытой ферментативной реакции. Эта схема, предложенная Сельковым и Каймачниковым [6], представляет собой вариант предыдущей модели Селькова.

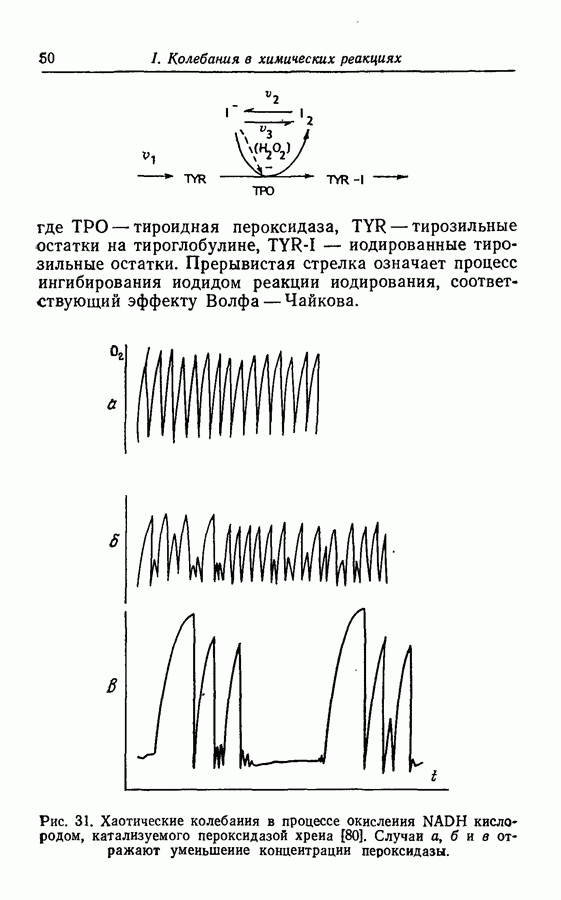
где  — субстрат, ингибирующий действие фермента Е; А, В — формы ферментов; Р — продукт.
— субстрат, ингибирующий действие фермента Е; А, В — формы ферментов; Р — продукт.

Здесь  — скорость образования
— скорость образования  — скорость превращения неактивной формы В в реагирующую форму, v — скорость реакции
— скорость превращения неактивной формы В в реагирующую форму, v — скорость реакции  .
.
Заменив S и А на х и у соответственно, можно получить дифференциальные уравнения в виде

где  При решении этой системы уравнений получаются множественные предельные
При решении этой системы уравнений получаются множественные предельные

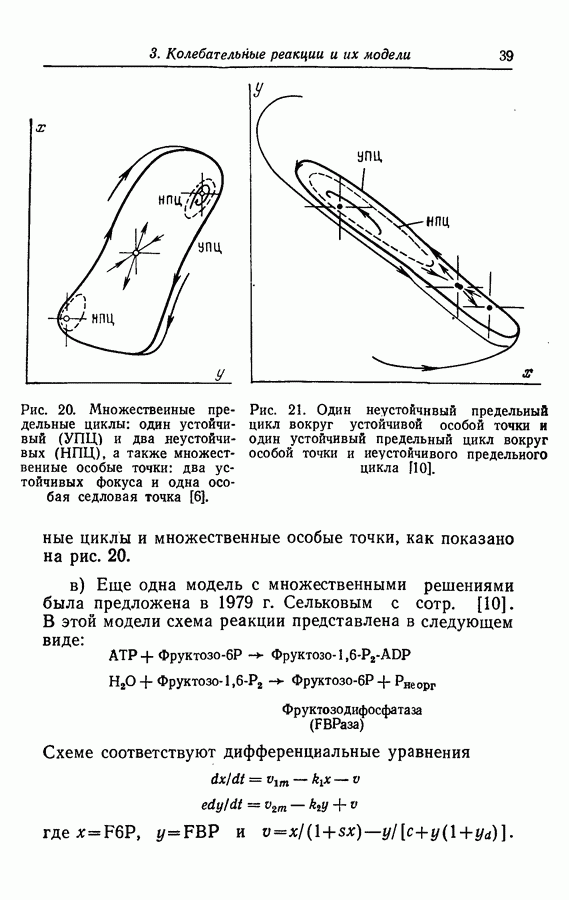
Рис. 20. Множественные предельные циклы: один устойчивый (УПЦ) и два неустойчивых (НПЦ), а также множественные особые точки: два устойчивых фокуса и одна особая седловая точка [6].

Рис. 21. Один неустойчивый предельный цикл вокруг устойчивой особой точки и один устойчивый предельный цикл вокруг особой точки и неустойчивого предельного цикла [10].
циклы и множественные особые точки, как показано на рис. 20.
в) Еще одна модель с множественными решениями была предложена в 1979 г. Сельковым с сотр. [10]. В этой модели схема реакции представлена в следующем виде:

Схеме соответствуют дифференциальные уравнения

где 
В этой модели устойчивые особые точки расположены внутри устойчивого предельного цикла и отделены от него неустойчивым предельным циклом (рис. 21).
Модель 5. Сосуществование устойчивого предельного цикла и устойчивой особой точки. В этой модели Дынника, Селькова и Семашко [За] рассматриваются гликолитические стадии, включающие реакции, катализируемые фосфофруктокиназой (PFK), аденилаткиназой (ADK) и обобщенным ферментом  .
.
Схема реакции:

Рассматриваются различные реакции:
1) Фосфорилирование фруктозо-6-фосфата F6P, катализируемое фосфофруктокиназой PFK.
2) Обратимое фосфорилирование ADP, катализируемое аденилаткиназой ADK.
3) Фосфорилирование ADP, катализируемое ферментом Ее, действие которого эквивалентно общему эффекту на гликолитических стадиях и стадиях окислительного фосфорилирования.
Дифференциальные уравнения для этой схемы имеют вид

При подстановке  дифференциальные уравнения принимают следующий вид:
дифференциальные уравнения принимают следующий вид:

и если  , то
, то

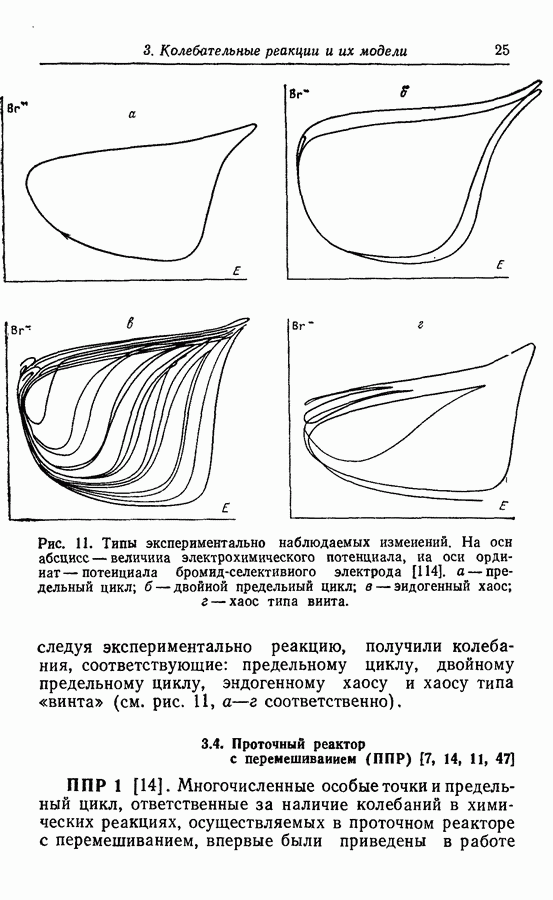
где v рассчитано из предыдущего выражения для V. Решения этих уравнений указывают на существование двух стационарных состояний  одно отвечает устойчивому (или неустойчивому) фокусу, другое — седловой точке. Получены следующие решения (рис. 22).
одно отвечает устойчивому (или неустойчивому) фокусу, другое — седловой точке. Получены следующие решения (рис. 22).
1. Нет ни одного особого решения в конечной области.
2. Единственное особое решение.
3. Два особых решения, одно седло  один неустойчивый фокус
один неустойчивый фокус  и устойчивый предельный цикл.
и устойчивый предельный цикл.
4.  устойчиво,
устойчиво,  — седло,
— седло,  окружено неустойчивым предельным циклом.
окружено неустойчивым предельным циклом.
5.  устойчиво,
устойчиво,  — седло,
— седло,  окружено неустойчивым предельным циклом, который также окружен устойчивым предельным циклом.
окружено неустойчивым предельным циклом, который также окружен устойчивым предельным циклом.
6. Si неустойчиво,  — седло.
— седло.

Рис. 22. Сосуществование устойчивого предельного цикла и устойчивой особой точки, окруженных неустойчивым предельным циклом [За].
Модель 6 [36]
Кинетическая схема

 — глицеральдегидфосфат
— глицеральдегидфосфат  — неорганический фосфат;
— неорганический фосфат;  — коферменты
— коферменты  — константа скорости введения
— константа скорости введения  — скорость введения
— скорость введения  и Ко — соответственно максимальная скорость введения и константа скорости протекания (просачивания)
и Ко — соответственно максимальная скорость введения и константа скорости протекания (просачивания) 
Считается, что реакции, катализируемые альдолазой (ALD) и триозофосфат-изомеразой, протекают с высокой скоростью и быстро достигается состояние равновесия. Таким образом, концентрации фруктозо-1,6-дифосфата (FDP), глицеральдегидфосфата (GAP) и дигидроксиаце-тонфосфата (DHAP) изменяются синфазно, что может быть записано как

где  — константы равновесия соответствующих реакций. Выведены дифференциальные уравнения
— константы равновесия соответствующих реакций. Выведены дифференциальные уравнения

в которых

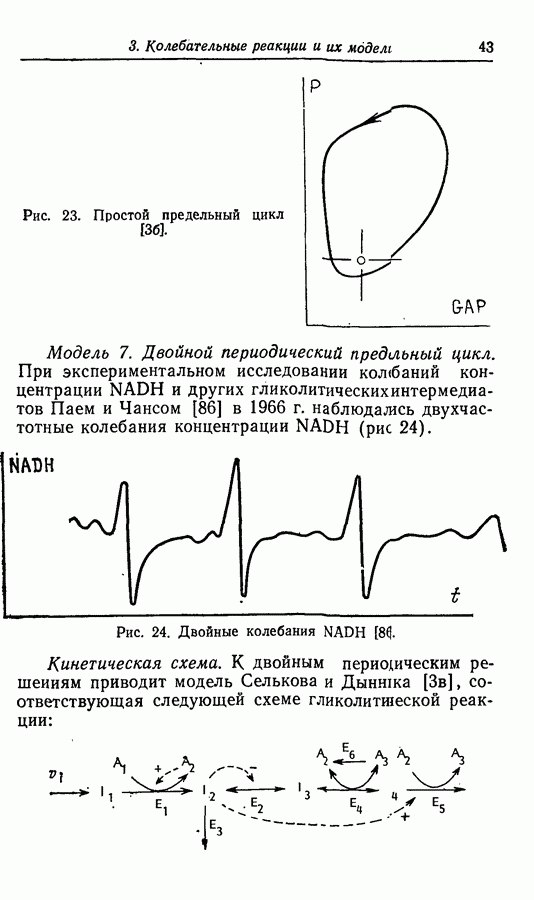
Полученный в качестве решения этих уравнений предельный цикл приведен на рис. 23.

Рис. 23. Простой предельный цикл [36].
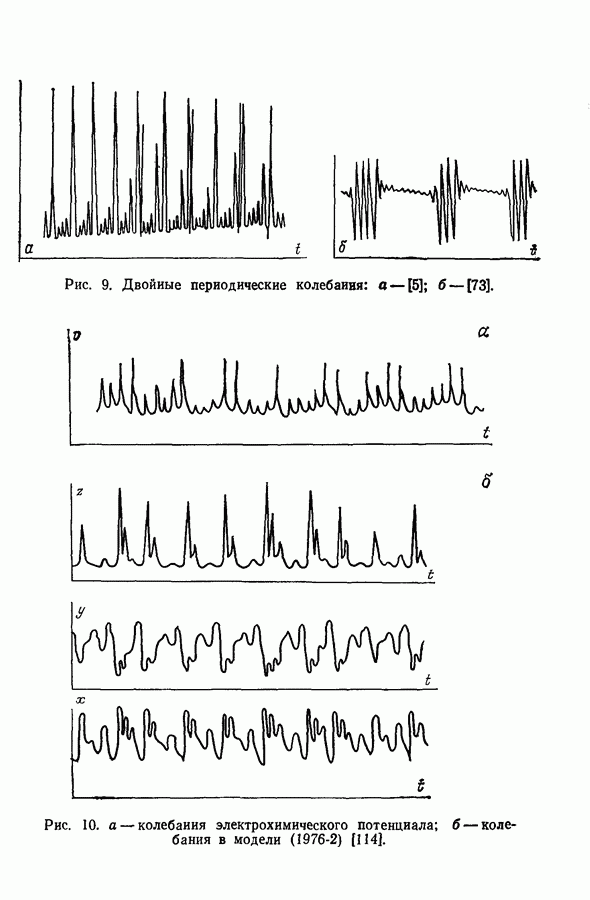
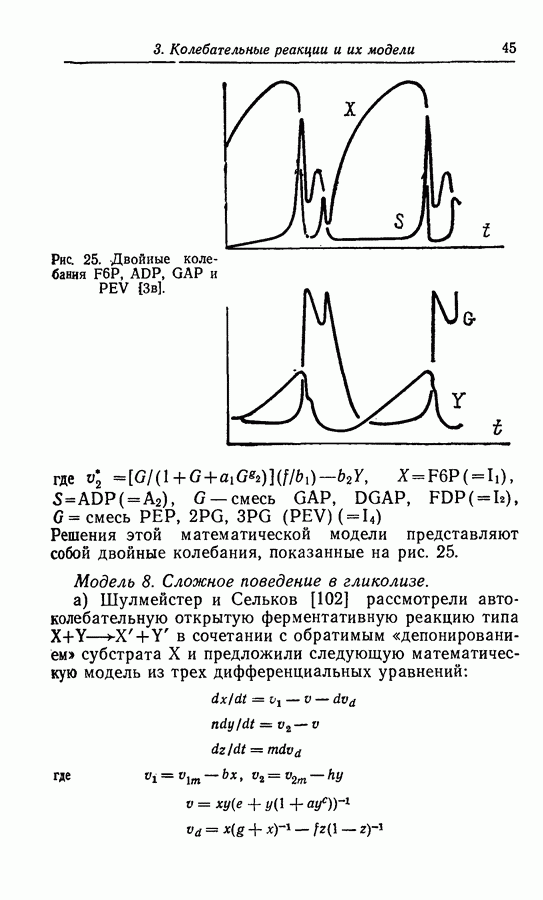
Модель 7. Двойной периодический предтьный цикл. При экспериментальном исследовании колебаний концентрации NADH и других гликолитических интермедиатов Паем и Чансом [86] в 1966 г. наблюдались двухчастотные колебания концентрации NADH (рис 24).

Рис. 24. Двойные колебания NADH [8].
Кинетическая схема. К двойным периоцическим решениям приводит модель Селькова и Дынника [3в], соответствующая следующей схеме гликолитической реакции:

где  глицеральдегидфосфат-дегидрогеназа (GAPDH);
глицеральдегидфосфат-дегидрогеназа (GAPDH);  - глицерофосфат-дегидрогеназа
- глицерофосфат-дегидрогеназа  фосфатглицераткиназа
фосфатглицераткиназа  пируваткиназа
пируваткиназа  обобщенная АТРаза;
обобщенная АТРаза;  смесь глицеральдегид-фосфата (GAP), дигидроксиацетонфосфата (DHAP) и
смесь глицеральдегид-фосфата (GAP), дигидроксиацетонфосфата (DHAP) и  смесь фосфоенолпирувата (РЕР),
смесь фосфоенолпирувата (РЕР),  -фосфоглицерата
-фосфоглицерата  ); и
); и  и АТР соответственно. На схеме пунктирными линиями обозначены активация PFK продуктом ADP, активация
и АТР соответственно. На схеме пунктирными линиями обозначены активация PFK продуктом ADP, активация  и ингибирование GAPDH субстратом
и ингибирование GAPDH субстратом 
Математическая модель. Кинетическое уравнение для скорости фосфофруктокиназиой (PFK) реакции, предложенное Сельковым и Бетцем [105], имеет вид

Скорость реакции, катализируемой глицеральдегид-фосфатдегидрогеназой GAPDH, Дынник и Сельков [36] представили уравнением

В той же работе дано уравнение для скорости реакции, катализируемой  -глицерофосфатдегидрогеназой
-глицерофосфатдегидрогеназой  :
:

Соответственно скорости реакций, катализируемых  записываются следующим образом:
записываются следующим образом:

Исключив быструю переменную Z, получаем


Рис. 25. Двойные колебания 
где  — смесь GAP, DGAP,
— смесь GAP, DGAP,  смесь
смесь 
Решения этой математической модели представляют собой двойные колебания, показанные на рис. 25.
Модель 8. Сложное поведение в гликолизе. а) Шулмейстер и Сельков [102] рассмотрели автоколебательную открытую ферментативную реакцию типа  в сочетании с обратимым «депонированием» субстрата X и предложили следующую математическую модель из трех дифференциальных уравнений:
в сочетании с обратимым «депонированием» субстрата X и предложили следующую математическую модель из трех дифференциальных уравнений:


Рис. 26. "Складчатый" предельный цикл [102].
Решения математической модели. Периодическим решением с несколькими максимумами, как показали авторы, является «складчатый» (folded) предельный цикл (рис. 26).
б) Другая, предложенная Шулмейстером, модель также состоит из трех дифференциальных уравнений:

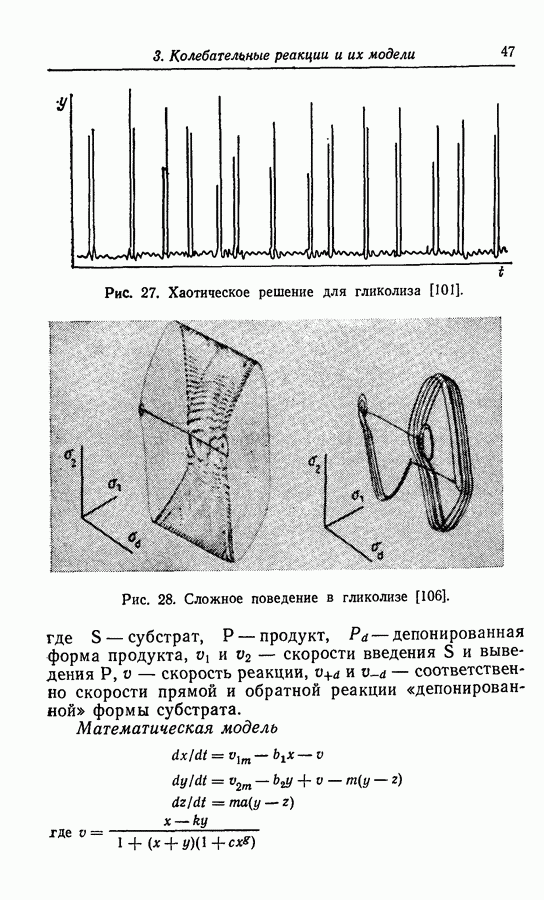
где  — гликоген). Решения этой модели соответствуют хаотическим колебаниям (рис. 27).
— гликоген). Решения этой модели соответствуют хаотическим колебаниям (рис. 27).
в) Еще одно сложное периодическое решение получено Сельковым [106] (рис. 28).
г) Каймачниковым и Шулмейстером [63] была изучена и описана открытая односубстратная ферментативная реакция с субстратным ингибированием и обратимым «депонированием» продукта.
Схема реакции


Рис. 27. Хаотическое решение для гликолиза [101].

Рис. 28. Сложное поведение в гликолизе [106].
где S — субстрат, Р — продукт,  — депонированная форма продукта,
— депонированная форма продукта,  — скорости введения S и выведения Р, v — скорость реакции,
— скорости введения S и выведения Р, v — скорость реакции,  — соответственно скорости прямой и обратной реакции «депонированной» формы субстрата.
— соответственно скорости прямой и обратной реакции «депонированной» формы субстрата.
Математическая модель


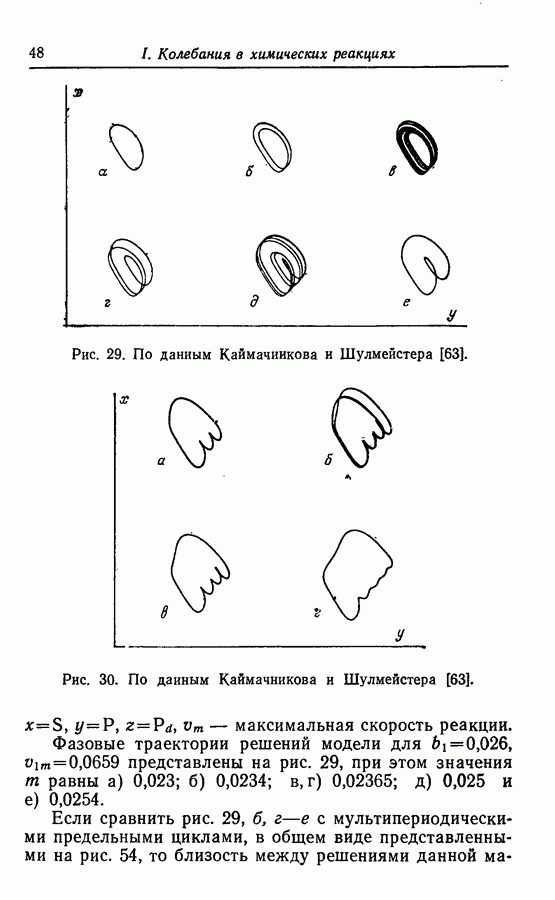
Рис. 29. По данным Каймачиикова и Шулмейстера [63].

Рис. 30. По данным Каймачиикова и Шулмейстера [63].
 — максимальная скорость реакции.
— максимальная скорость реакции.
Фазовые траектории решений модели для  представлены на рис. 29, при этом значения
представлены на рис. 29, при этом значения  равны а) 0,023; б) 0,0234; в, г) 0,02365; д) 0,025 и е) 0,0254.
равны а) 0,023; б) 0,0234; в, г) 0,02365; д) 0,025 и е) 0,0254.
Если сравнить рис. 29, б, г - е с мультипериодическими предельными циклами, в общем виде представленными на рис. 54, то близость между решениями данной
математической модели и возможными типами предельных циклов, полученных в общем виде, становится очевидной.
Кроме решений, представленных на рис. 29, Шулмейстером и Каймачниковым [63] был получен набор решений, соответствующих более сложному поведению системы (рис. 30).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. КОЛЕБАНИЯ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 3. Колебательные реакции и их модели
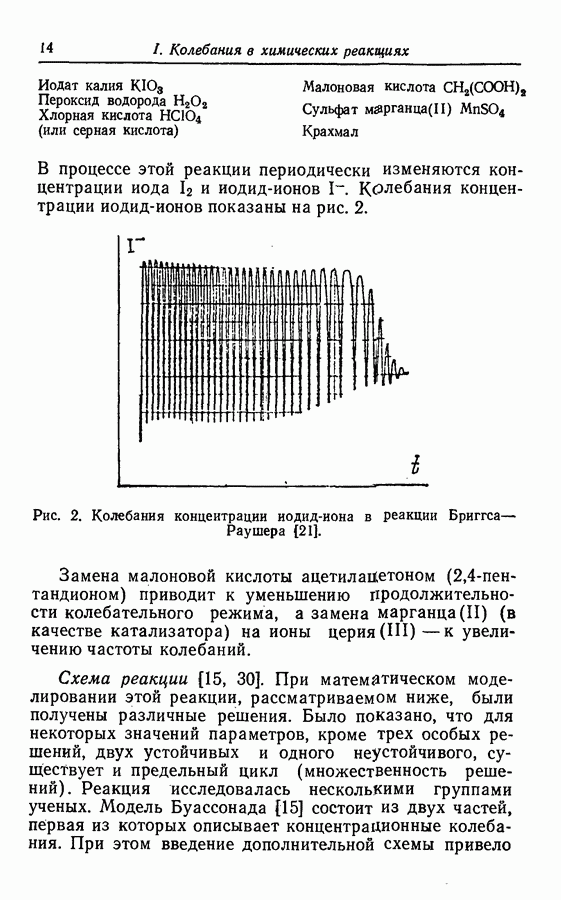
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
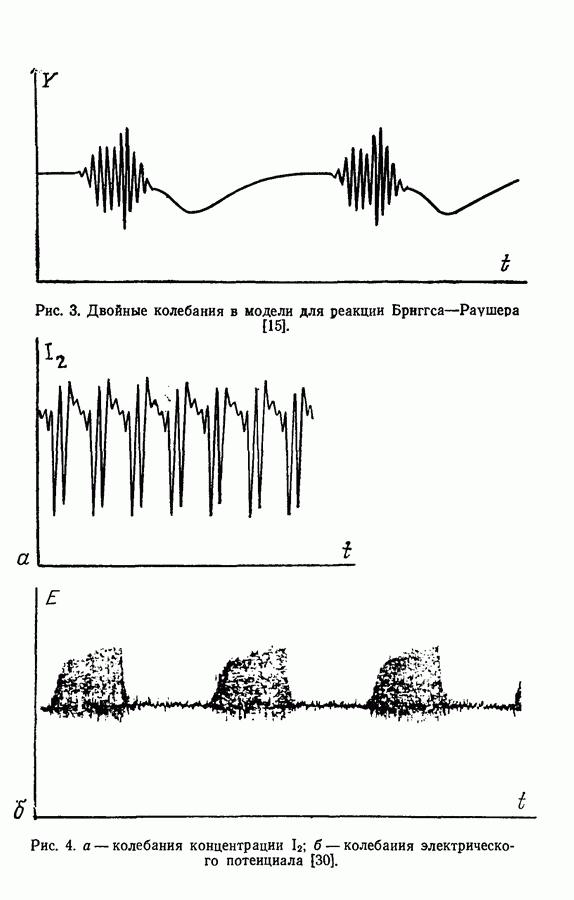
- 3.2. Периодические водные часы (реакция Бриггса—Раушера) [21]
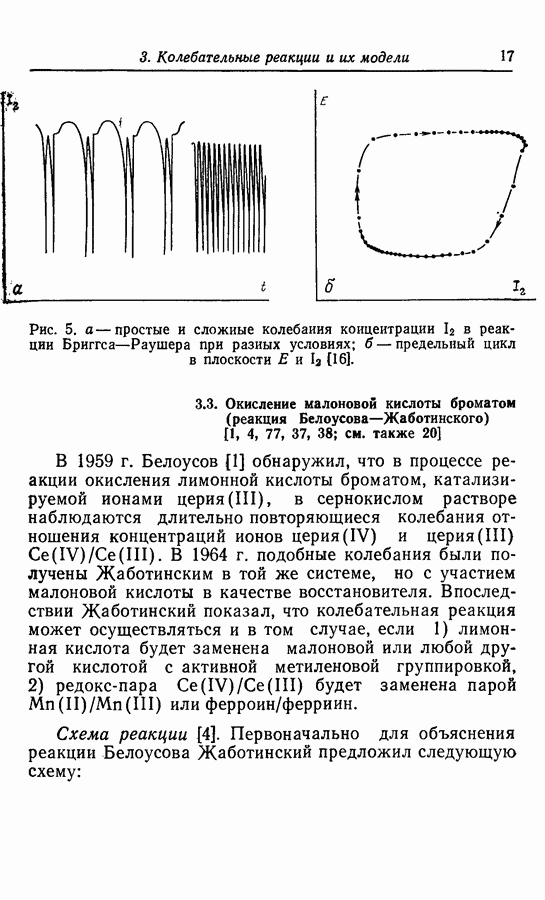
- 3.3. Окисление малоновоб кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием (ППР) [7, 14, II, 47]
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций и их модели
- 3.11. Некаталитические реакции
- 3.12. Таблица колебательных реакций
- 4. Характеристики колебательных систем
- 4.2. Нелинейность систем
- 4.3. Параметры системы
- 4.4. Число решений
- 5. Глобальный анализ
- 5.2. Бифуркации как способ поиска колебаний
- 6. Классификация колебаний
- 6.2. Типы компонентов колебательных химических реакций
- 6.3. Типы колебательных математических решений
- 7. Состояние исследований и дальнейшие направления их развития
- Часть II. РАЗВИТИЕ ИССЛЕДОВАНИЙ ХИМИЧЕСКИХ КОЛЕБАНИЙ В ПОСЛЕДНЕЕ ВРЕМЯ
- 3. Реакции и модели, проявляющие колебания
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Колебательные йодные часы (реакция Бриггса—Раушера)
- 3.3. Окисление малоновой кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций
- 3.11. Некаталитические реакции
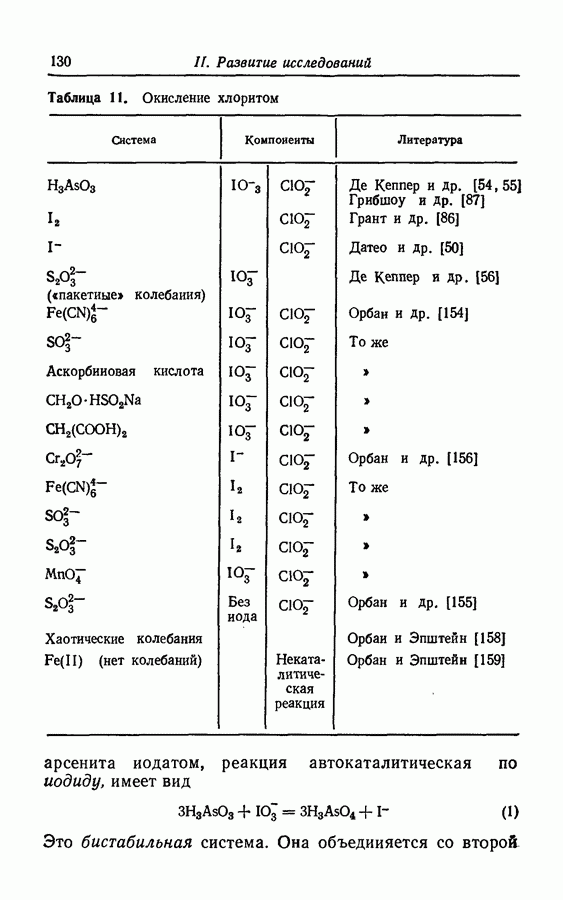
- 3.12. Окисление хлоритом
- 3.13. Разноплановые исследования
- 3.14. Общие модели и математические методы