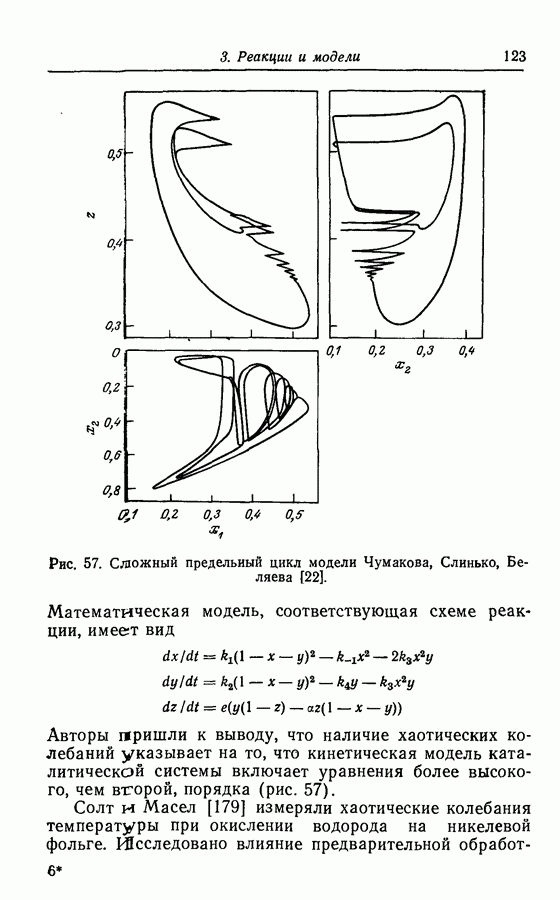
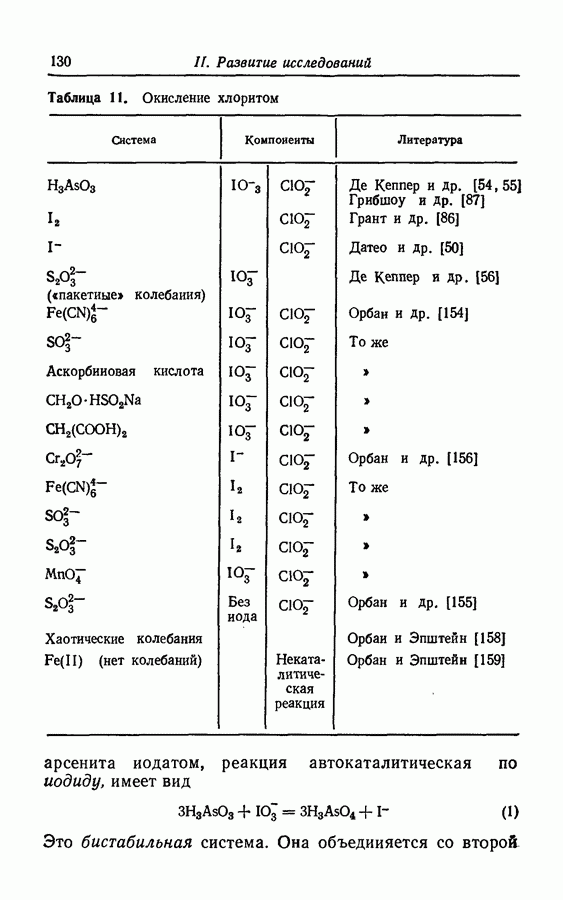
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Характеристики колебательных систем
Колебания представляют собой специфические решения динамических систем. Эти решения можно не только получить, но и установить некоторые различия между ними. Одним из факторов, приводящих к различным решениям, является размерность системы. (Ниже рассмотрены различные формы основных колебательных решений для разных размерностей.) Показано, что при увеличении размерности увеличиваются также возможности получения разнообразных колебательных решений.
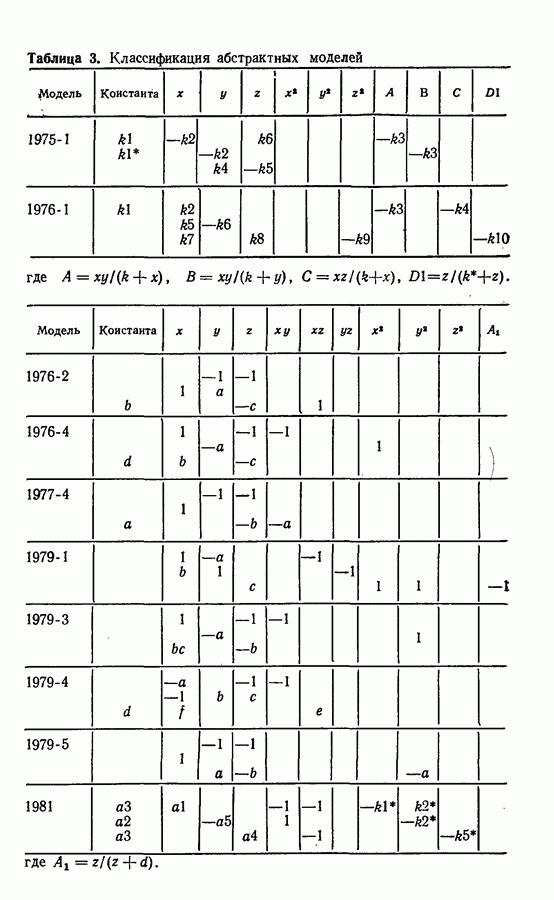
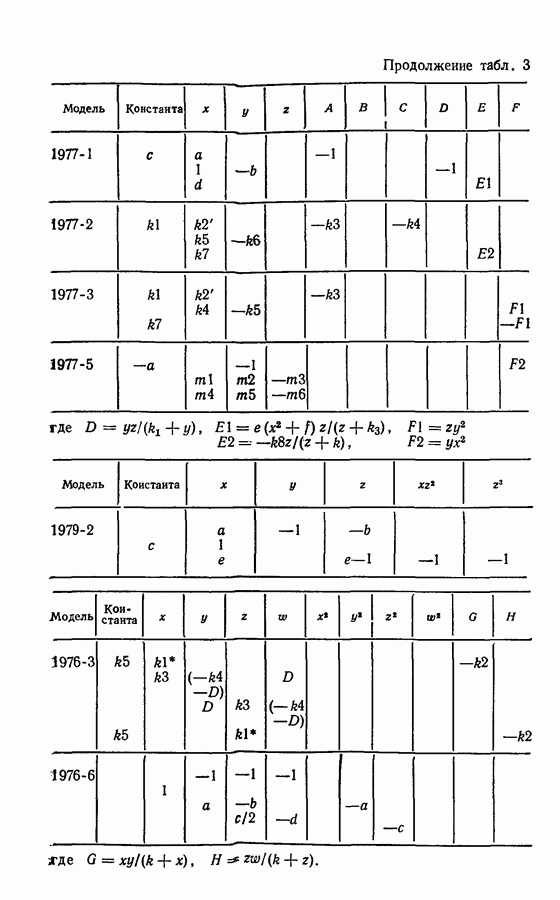
Другим элементом, определяющим возможность появления и вид колебательных решений, является нелинейность системы. Далее приводится классификация известных химических моделей, основанная на признаке нелинейности, в которой показано, что модели, описанные в работах различных исследователей, могут быть сгруппированы в определенные классы.
4.1. Размерность системы
Размерность химической системы определяется числом реагентов. Минимальная размерность равна единице, однако с точки зрения рассматриваемого здесь материала более интересны системы по крайней мере с двумя компонентами, т. е. взаимодействие хотя бы между двумя частицами. В математических терминах решение — это линия, представляющая функцию элемента времени  . Это решение имеет две основные дифференциальные формы, рассматриваемые ниже.
. Это решение имеет две основные дифференциальные формы, рассматриваемые ниже.
Решение  — это линия в плоскости
— это линия в плоскости  . В пространстве, размерность которого больше единицы, полное решение можно представить в виде линии, включенной в это пространство. В пространствах различной размерности получаются отличающиеся решения в связи с различием геометрии этих пространств. Таким образом, мы получаем разнообразные возможности решений в результате увеличения размерности.
. В пространстве, размерность которого больше единицы, полное решение можно представить в виде линии, включенной в это пространство. В пространствах различной размерности получаются отличающиеся решения в связи с различием геометрии этих пространств. Таким образом, мы получаем разнообразные возможности решений в результате увеличения размерности.
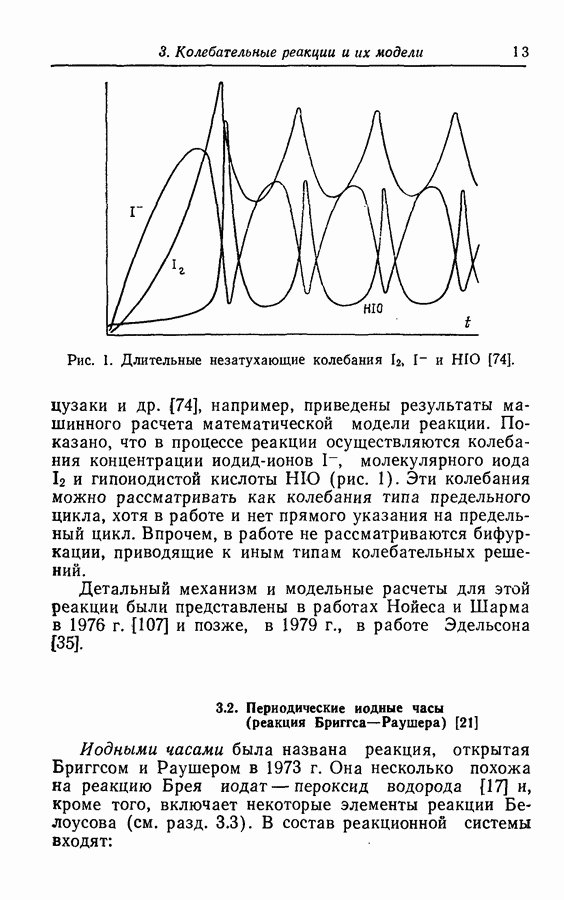
Система с размерностью, равной единице (ограниченность решения). Традиционно наблюдаемые колебания

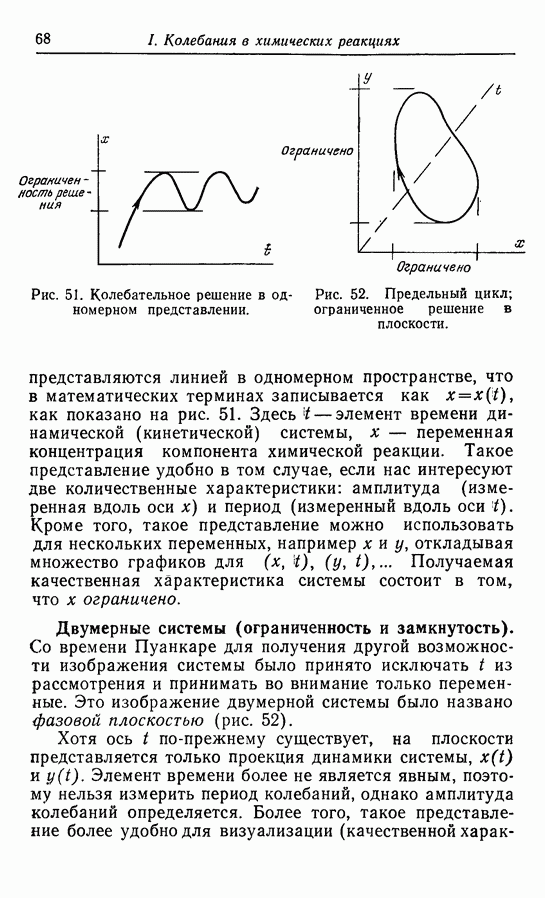
Рис. 51. Колебательное решение в одномерном представлении.

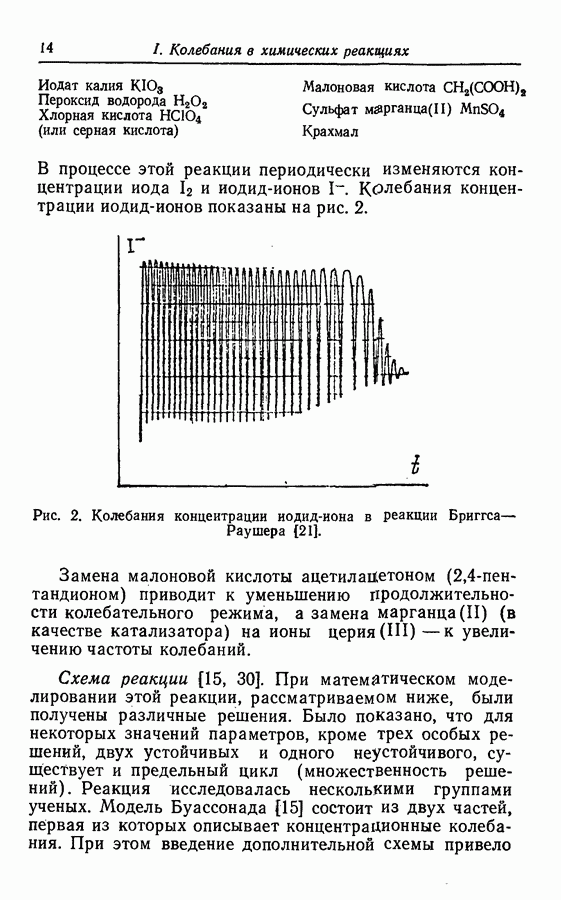
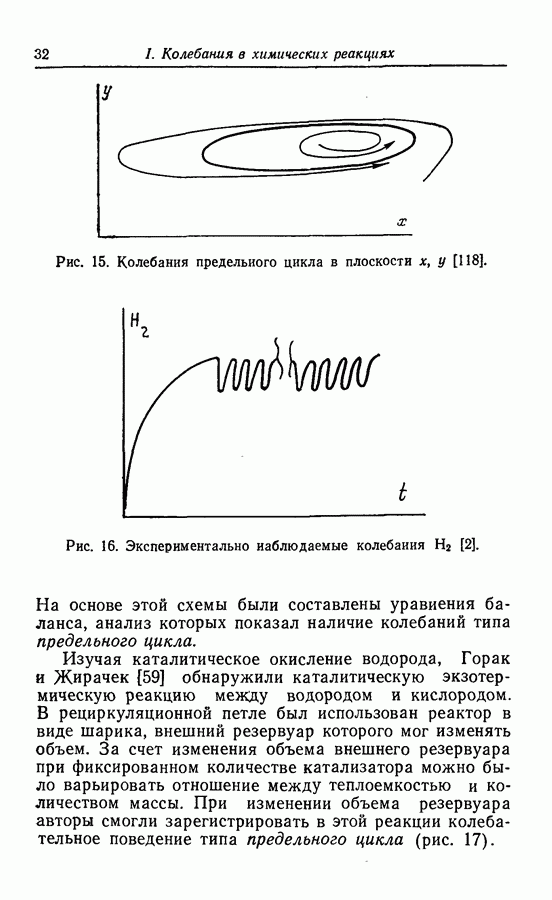
Рис. 52. Предельный цикл; ограниченное решение в плоскости.
представляются линией в одномерном пространстве, что в математических терминах записывается как  как показано на рис. 51. Здесь
как показано на рис. 51. Здесь  — элемент времени динамической (кинетической) системы, х — переменная концентрация компонента химической реакции. Такое представление удобно в том случае, если нас интересуют две количественные характеристики: амплитуда (измеренная вдоль оси х) и период (измеренный вдоль оси t). Кроме того, такое представление можно использовать для нескольких переменных, например х и у, откладывая множество графиков для
— элемент времени динамической (кинетической) системы, х — переменная концентрация компонента химической реакции. Такое представление удобно в том случае, если нас интересуют две количественные характеристики: амплитуда (измеренная вдоль оси х) и период (измеренный вдоль оси t). Кроме того, такое представление можно использовать для нескольких переменных, например х и у, откладывая множество графиков для  Получаемая качественная характеристика системы состоит в том, что х ограничено.
Получаемая качественная характеристика системы состоит в том, что х ограничено.
Двумерные системы (ограниченность и замкнутость).
Со времени Пуанкаре для получения другой возможности изображения системы было принято исключать t из рассмотрения и принимать во внимание только переменные. Это изображение двумерной системы было названо фазовой плоскостью (рис. 52).
Хотя ось t по-прежнему существует, на плоскости представляется только проекция динамики системы,  Элемент времени более не является явным, поэтому нельзя измерить период колебаний, однако амплитуда колебаний определяется. Более того, такое представление более удобно для визуализации (качественной характеристики)
Элемент времени более не является явным, поэтому нельзя измерить период колебаний, однако амплитуда колебаний определяется. Более того, такое представление более удобно для визуализации (качественной характеристики)

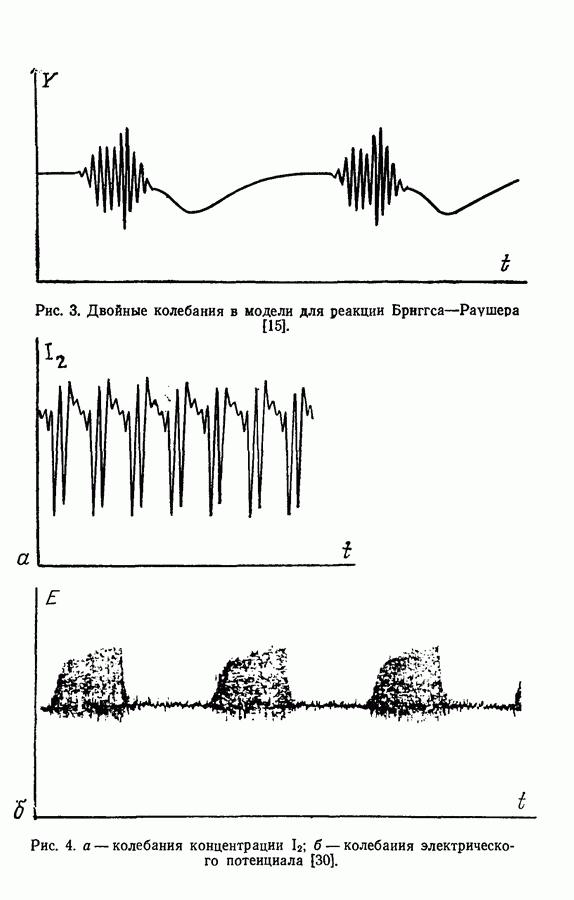
Рис. 53. Площади, ограниченные выгнутым и вогнутым предельными циклами.
системы, чем для измерения количественных характеристик.
В двумерном пространстве, в плоскости, наиболее поразительное решение — это замкнутая кривая, названная Пуанкаре предельным циклом. Предельный цикл ограничен и замкнут и представляет собой периодическое решение рассматриваемых в настоящей книге динамических систем.
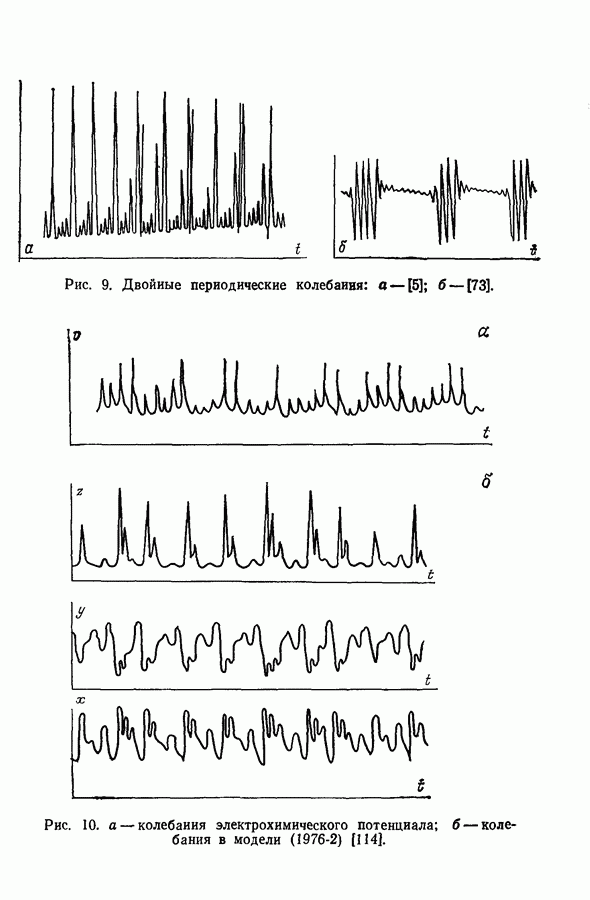
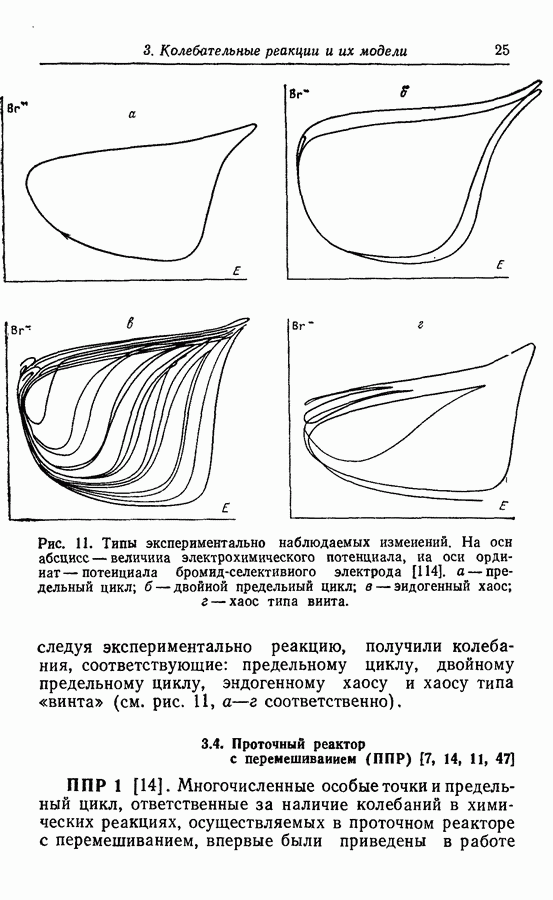
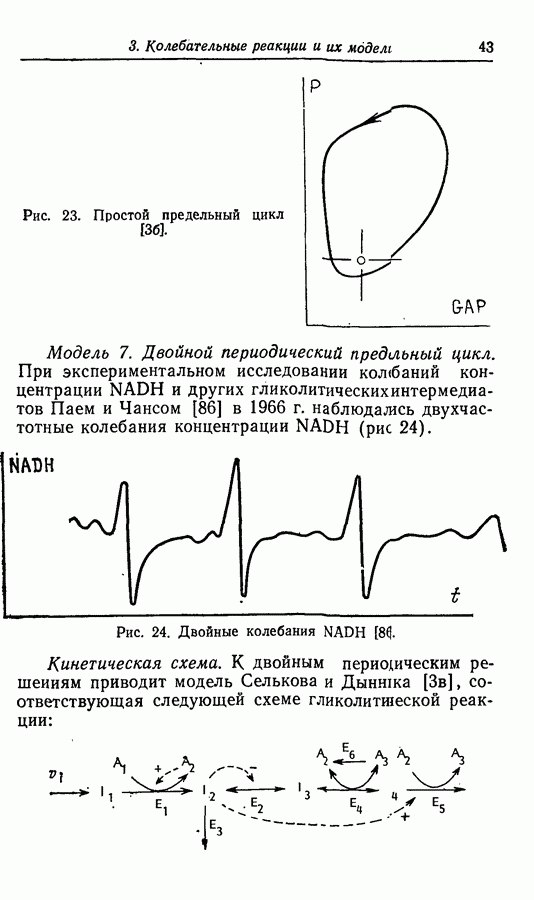
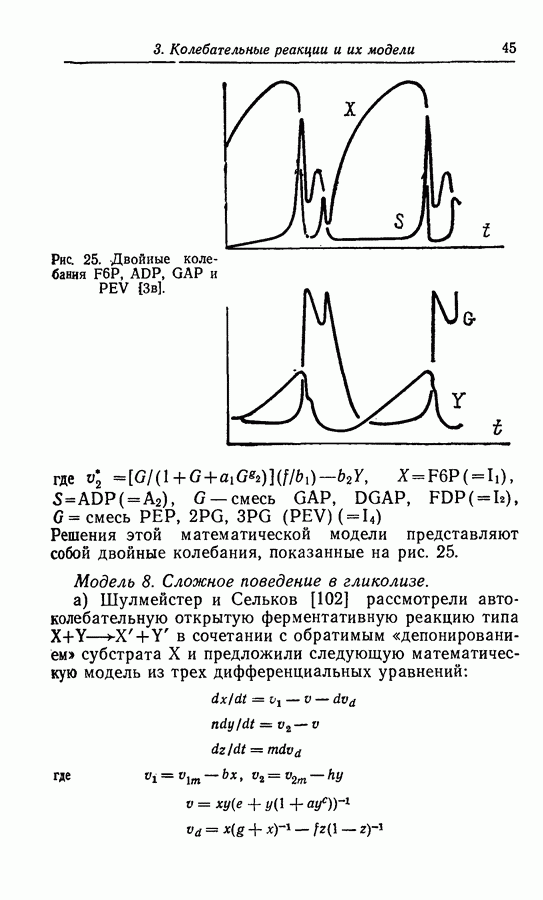
Одна из важных качественных характеристик двумерных решений связана с концепцией выгнутости пространства, ограниченного замкнутым решением, т. е. предельным циклом. Легко представить изображение  в котором для выгнутого предельного цикла будут наблюдаться плавные колебания как х, так и у, а для вогнутого предельного цикла — колебания со множественностью величин периодов (рис. 53). Очевидно, что описанные в разд. 3 «двойные колебания» относятся к последнему типу предельных циклов.
в котором для выгнутого предельного цикла будут наблюдаться плавные колебания как х, так и у, а для вогнутого предельного цикла — колебания со множественностью величин периодов (рис. 53). Очевидно, что описанные в разд. 3 «двойные колебания» относятся к последнему типу предельных циклов.
И выгнутый, и вогнутый предельные циклы могут быть преобразованы (растянуты) в круг, и, таким образом, единственным периодическим решением двумерной динамической системы является предельный цикл. Предельный цикл ограничен как со стороны оси х, так и со стороны оси у. Кроме того, по определению предельный Цикл — это замкнутая кривая.
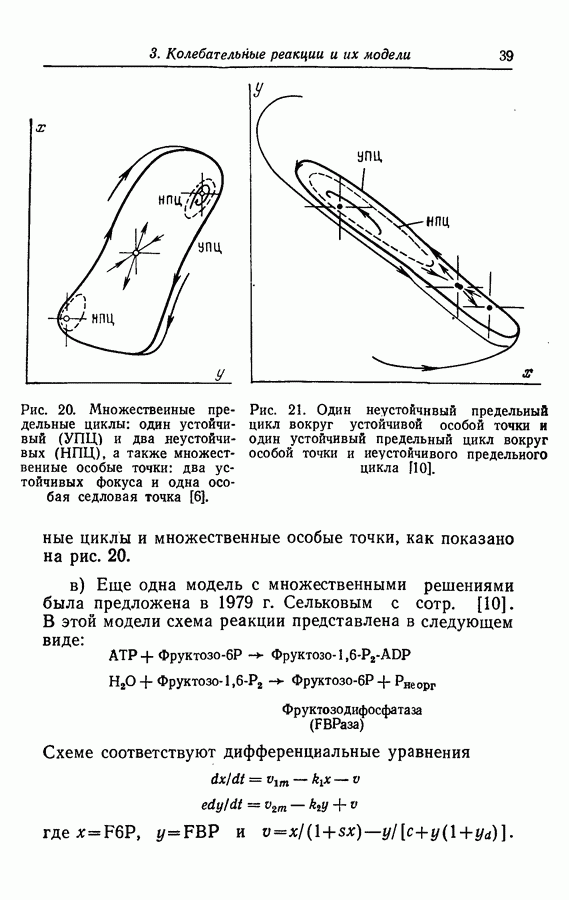
Необходимо также отметить, что в двумерном пространстве могут быть получены и множественные предельные

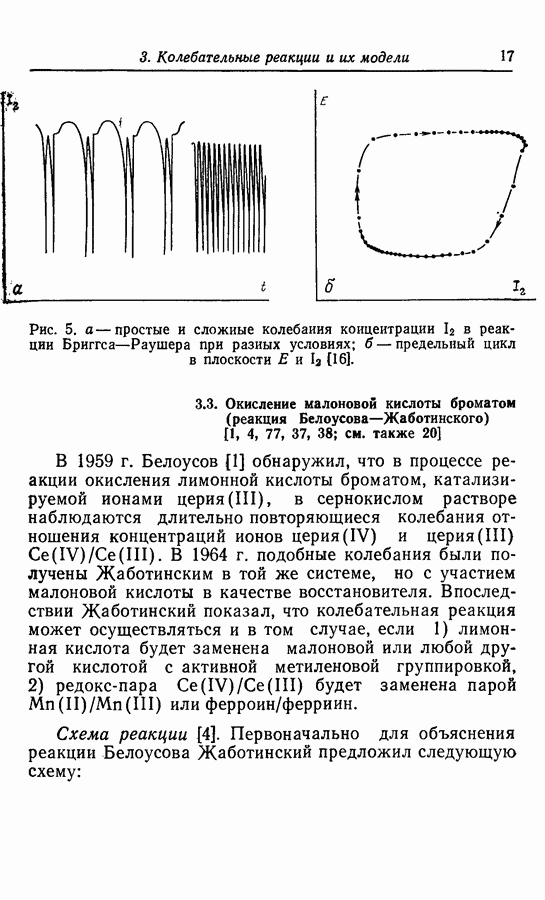
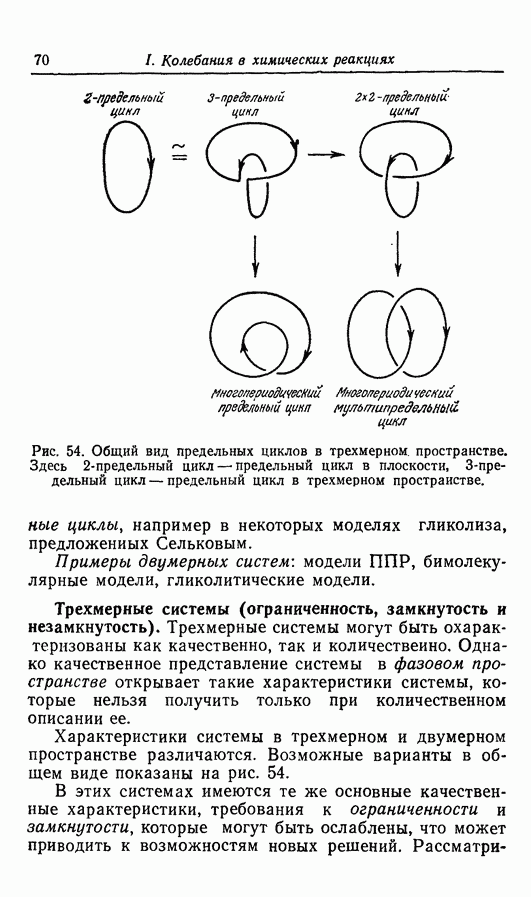
Рис. 54. Общий вид предельных циклов в трехмерном, пространстве. Здесь 2 - предельный цикл — предельный цикл в плоскости, 3 - предельный цикл — предельный цикл в трехмерном пространстве.
циклы, например в некоторых моделях гликолиза, предложенных Сельковым.
Примеры двумерных систем: модели ППР, бимолекулярные модели, гликолитические модели.
Трехмерные системы (ограниченность, замкнутость и незамкнутость). Трехмерные системы могут быть охарактеризованы как качественно, так и количественно. Однако качественное представление системы в фазовом пространстве открывает такие характеристики системы, которые нельзя получить только при количественном описании ее.
Характеристики системы в трехмерном и двумерном пространстве различаются. Возможные варианты в общем виде показаны на рис. 54.
В этих системах имеются те же основные качественные характеристики, требования к ограниченности и замкнутости, которые могут быть ослаблены, что может приводить к возможностям новых решений. Рассматривая
функциональную размерность ( -размерность) математических решений (см. Гарел [55]), можно выделить граничные решения в трехмерном пространстве, имеющие три различные формы:
-размерность) математических решений (см. Гарел [55]), можно выделить граничные решения в трехмерном пространстве, имеющие три различные формы:
нуль  размерная: (открытая) точка взрыва (ТВ)
размерная: (открытая) точка взрыва (ТВ)
одно  размерная: (замкнутая) предельный цикл (ПЦ)
размерная: (замкнутая) предельный цикл (ПЦ)
двух  размериая: (открытая) предельная поверхность (ПП)
размериая: (открытая) предельная поверхность (ПП)
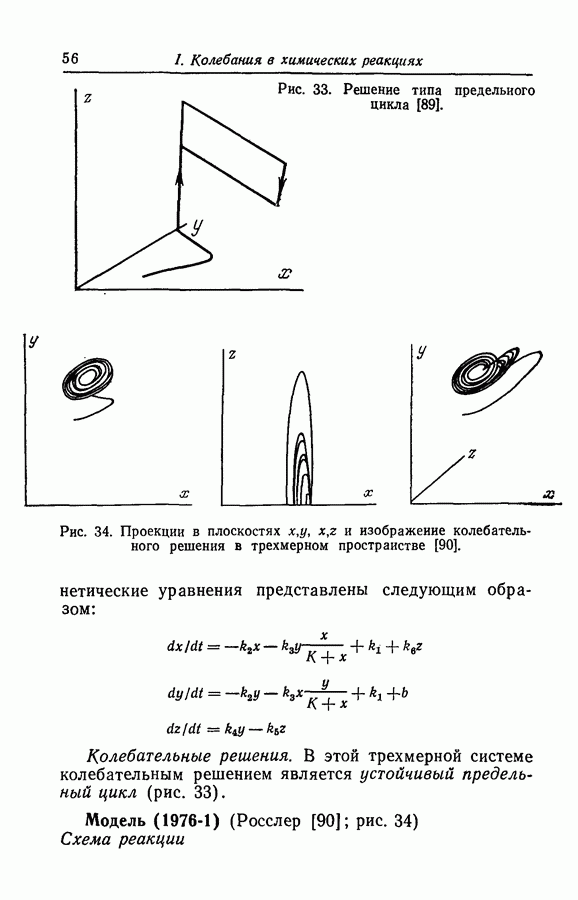
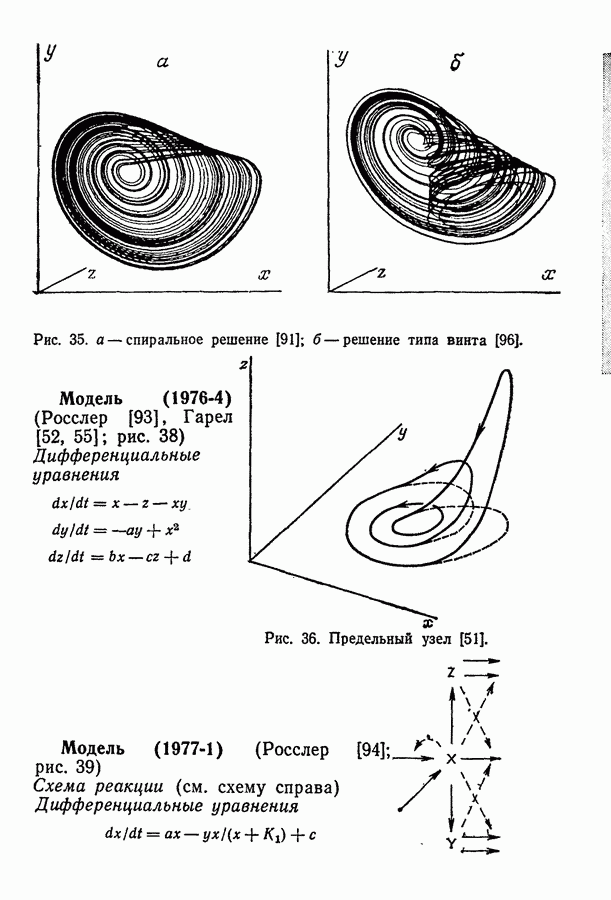
Примеры трехмерных систем: системы Бриггса — Раушера; реакция окисления малоновой кислоты; абстрактные модели Росслера.
Системы  -мерные
-мерные  Уже для трехмерной системы становится очевидным, что однозначные предельные циклы уступают место множественным периодическим решениям. При высоких размерностях могут встречаться и более запутанные решения. В частности, такими решениями могут быть гиперповерхности с различными характеристиками.
Уже для трехмерной системы становится очевидным, что однозначные предельные циклы уступают место множественным периодическим решениям. При высоких размерностях могут встречаться и более запутанные решения. В частности, такими решениями могут быть гиперповерхности с различными характеристиками.
Примеры четырехмерных систем: абстрактные модели (1976-3), (1979-6).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. КОЛЕБАНИЯ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 3. Колебательные реакции и их модели
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Периодические водные часы (реакция Бриггса—Раушера) [21]
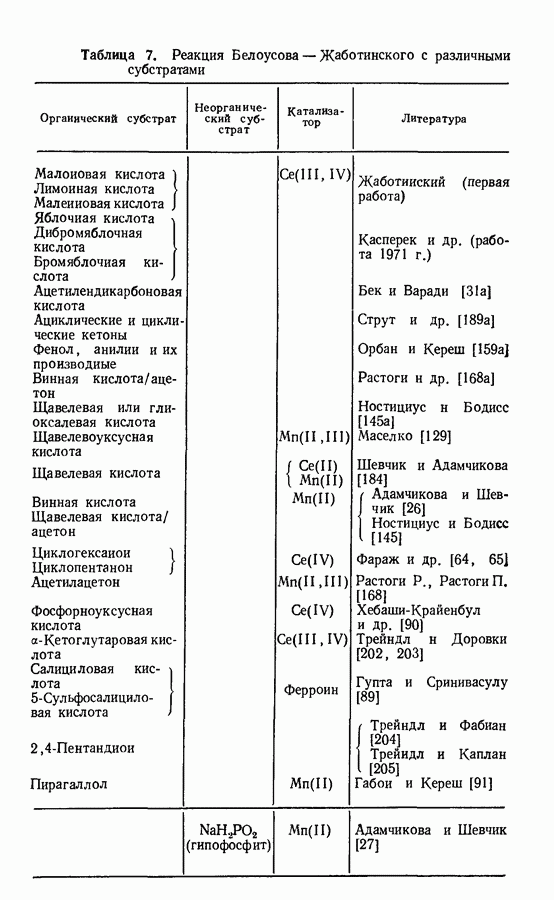
- 3.3. Окисление малоновоб кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием (ППР) [7, 14, II, 47]
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций и их модели
- 3.11. Некаталитические реакции
- 3.12. Таблица колебательных реакций
- 4. Характеристики колебательных систем
- 4.2. Нелинейность систем
- 4.3. Параметры системы
- 4.4. Число решений
- 5. Глобальный анализ
- 5.2. Бифуркации как способ поиска колебаний
- 6. Классификация колебаний
- 6.2. Типы компонентов колебательных химических реакций
- 6.3. Типы колебательных математических решений
- 7. Состояние исследований и дальнейшие направления их развития
- Часть II. РАЗВИТИЕ ИССЛЕДОВАНИЙ ХИМИЧЕСКИХ КОЛЕБАНИЙ В ПОСЛЕДНЕЕ ВРЕМЯ
- 3. Реакции и модели, проявляющие колебания
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Колебательные йодные часы (реакция Бриггса—Раушера)
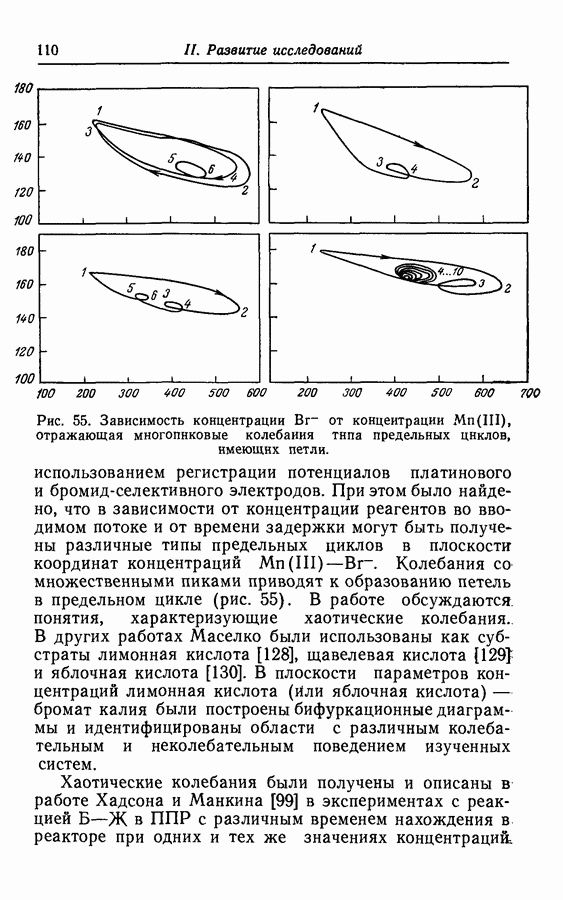
- 3.3. Окисление малоновой кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций
- 3.11. Некаталитические реакции
- 3.12. Окисление хлоритом
- 3.13. Разноплановые исследования
- 3.14. Общие модели и математические методы