| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Нелинейность систем
Нелинейность системы отражена в правой части дифференциальных уравнений, составляющих математическую модель в соответствии с кинетикой реакции. Такие дифференциальные уравнения — это кинетические уравнения, представляющие математическую модель данной химической схемы. Дифференциальные уравнения не только связывают константы скорости отдельных реакций (k), но и показывают, каким образом действует каждый компонент системы в одной или нескольких реакциях.
Нелинейность системы определяется типом взаимодействия компонентов системы, что в свою очередь приводит к частным типам решений, имеющих как колебательные, так и неколебательные характеристики.
Причиной нелинейности системы может быть взаимодействие продукта одной из стадий реакции с компонентом, контролирующим скорость этой стадии. Полученный
в результате такого взаимодействия тип нелинейности называется нелинейностью обратной связи.
Кроме того, математическое выражение правой части дифференциального уравнения определяется формой взаимодействия элементов системы. Используемые в различных моделях формы нелинейности и соответствующие примеры обсуждаются ниже.
Механизм обратной связи, приводящий к нелинейности. В некоторых системах нелинейность обусловлена тем, что продукт реакции возвращается на отдельной стадии в систему и либо активизирует, либо ингибирует реакцию, определяя формы нелинейности в реакционной схеме. Эти концепции были сформулированы Хиггинсом (1964 г.) в его статье [56].
Явление обратной связи известно; оно описано в химической литературе, например, в случае реакции Брея— Либавски [17], гликолиза [56], каталитического окисления водорода [2] (см. также обзорные статьи Гарела [48] и Франка [39] ).
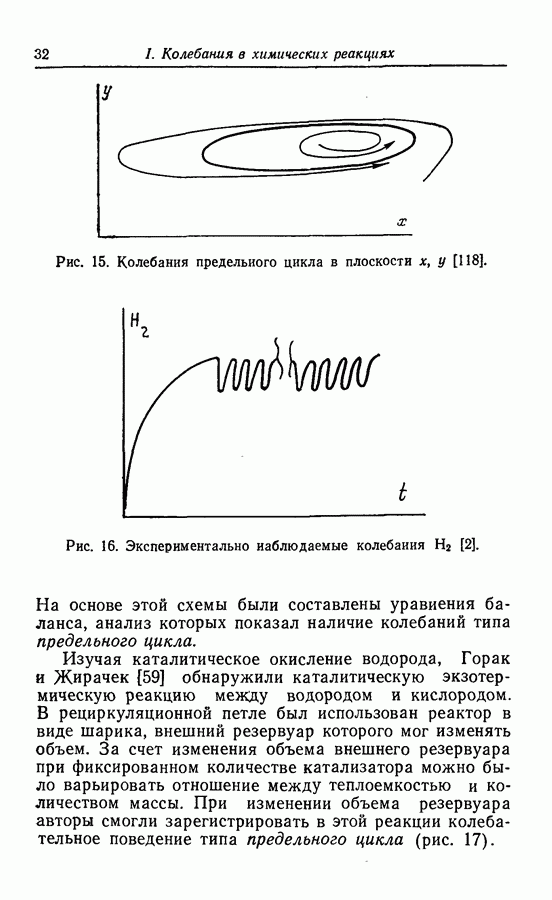
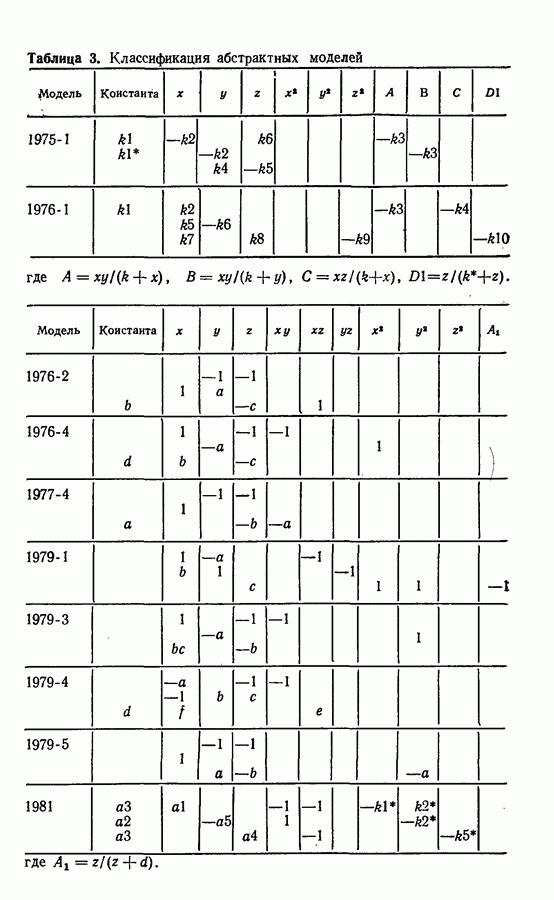
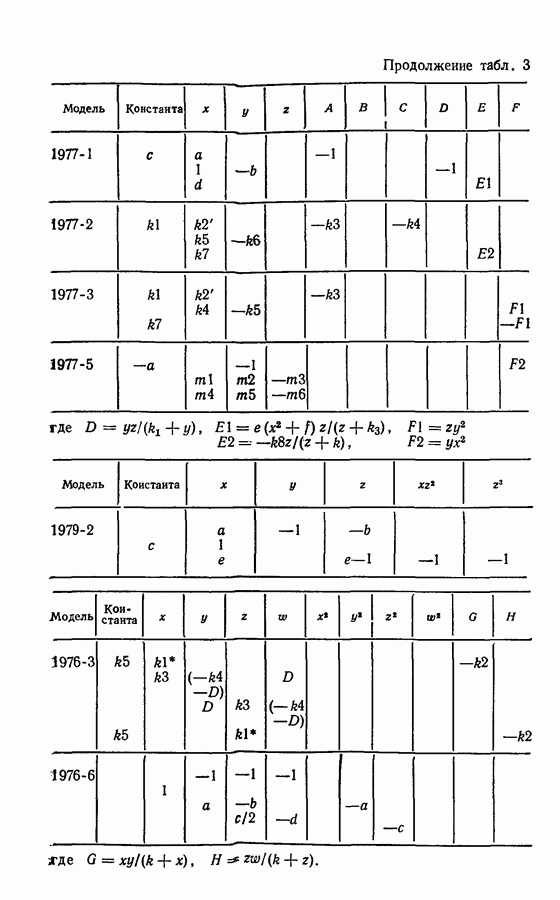
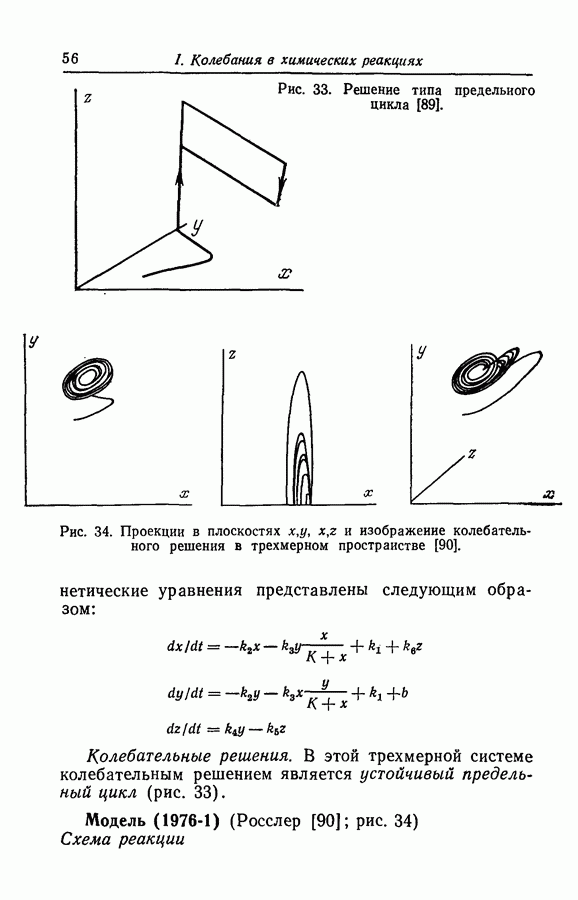
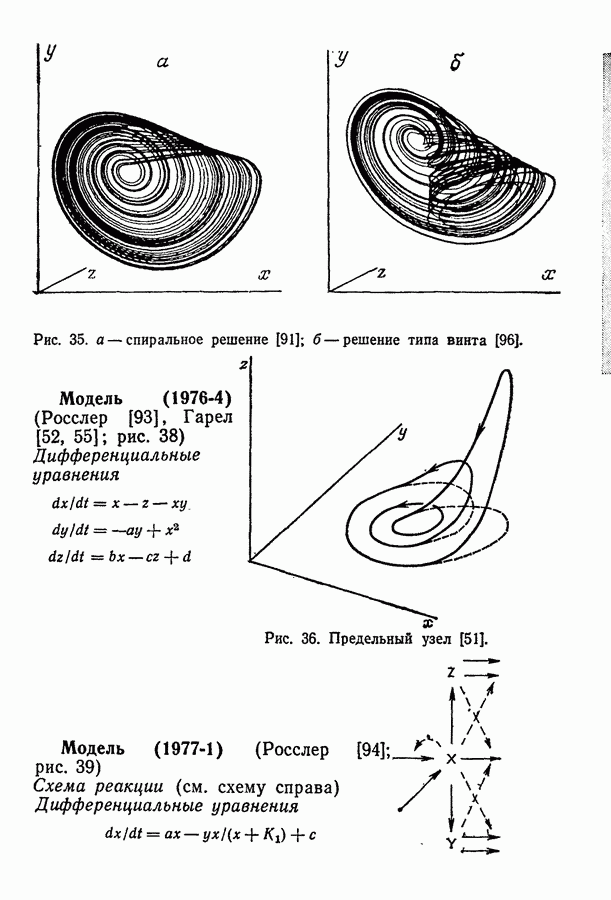
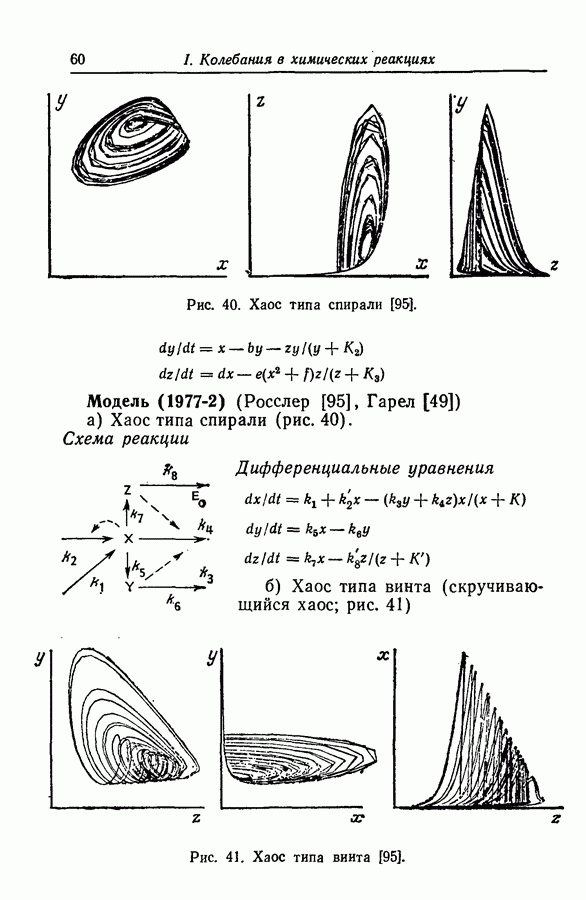
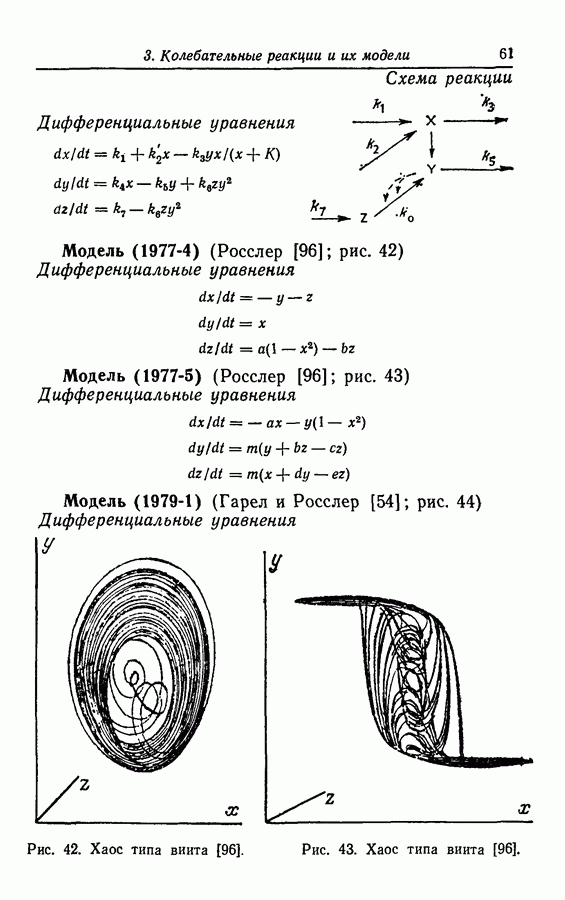
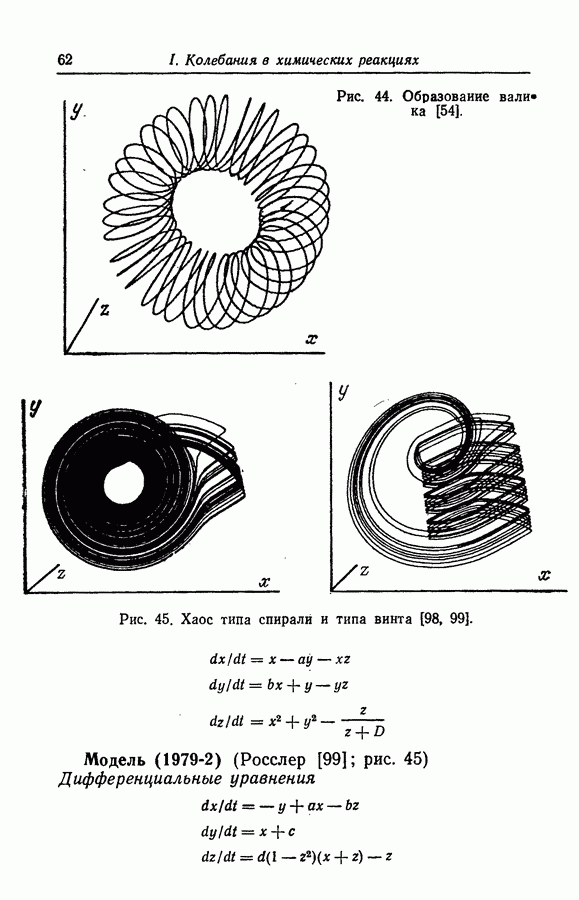
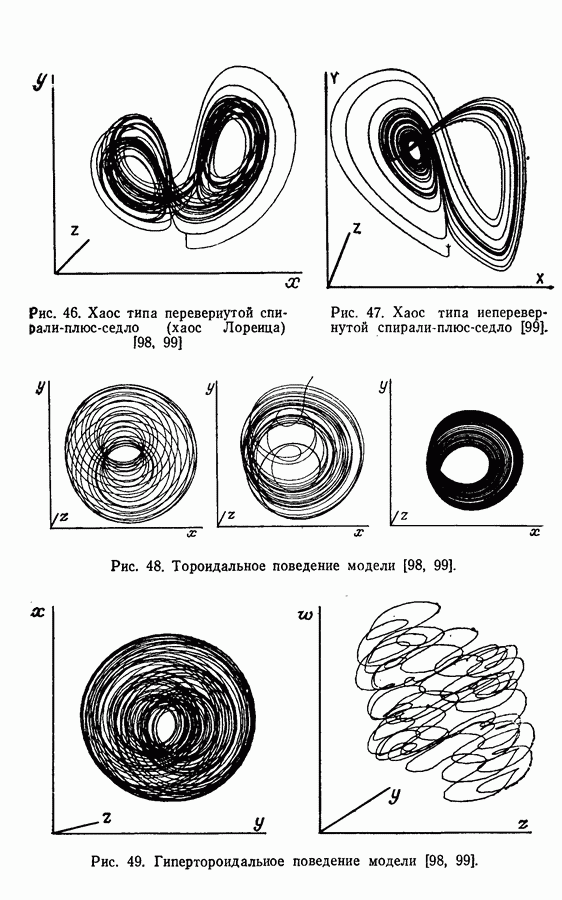
Нелинейность произведения. Этот класс нелинейностей составляют математические модели, включающие нелинейность, вызванную произведением переменных типа  и т. д. Подобная нелинейность может быть включена в значительное число колебательных реакций, примерами которых являются бимолекулярная модель [66], реакция Бриггса — Раушера [15], реакция Белоусова — Жаботинского [38], окисление СО [118], окисление дитионита натрия [31], абстрактные модели Росслера (1976-2 и 4), (1977-4 и 5), (1979-2 и далее), (1980) [91,93,96,99,115].
и т. д. Подобная нелинейность может быть включена в значительное число колебательных реакций, примерами которых являются бимолекулярная модель [66], реакция Бриггса — Раушера [15], реакция Белоусова — Жаботинского [38], окисление СО [118], окисление дитионита натрия [31], абстрактные модели Росслера (1976-2 и 4), (1977-4 и 5), (1979-2 и далее), (1980) [91,93,96,99,115].
Экспоненциальная нелинейность. В некоторых моделях, в частности моделях, имеющих приложения в химической технологии, нелинейность в уравнениях баланса тепла и массы выражается экспоненциальной величиной. Примеры экспоненциальной нелинейности описаны в литературе в связи с исследованием реакций в ППР [14, 11, 47], каталитического разложения  , каталитического окисления водорода [84].
, каталитического окисления водорода [84].
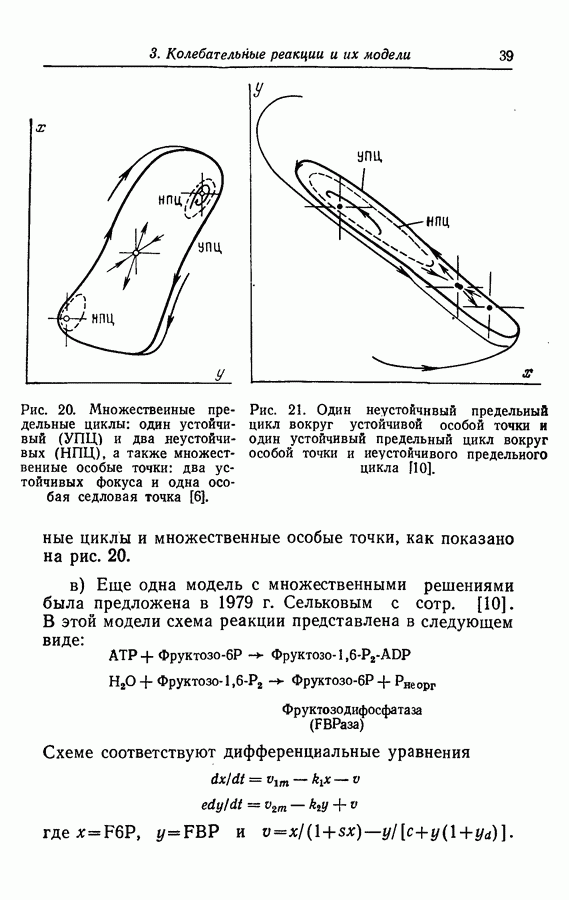
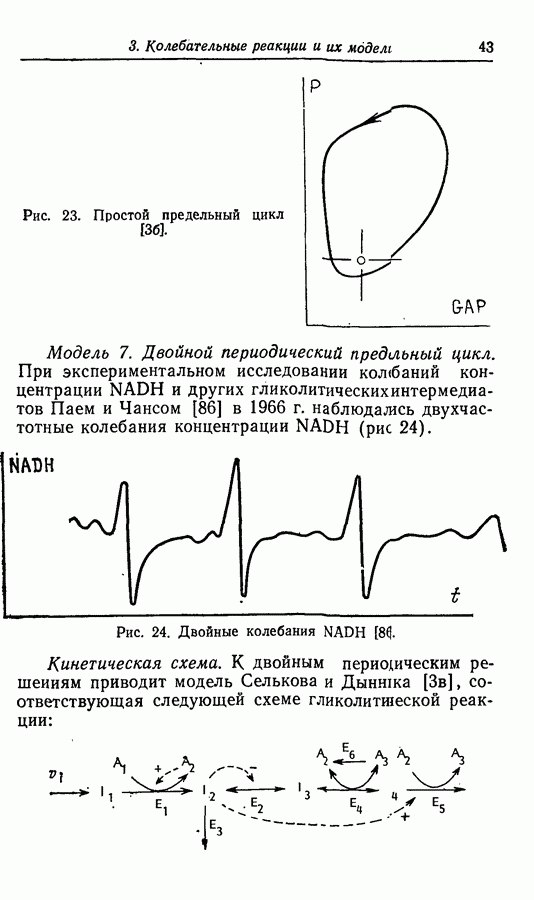
Рациональная нелинейность. Во многих моделях нелинейность вводится в виде рациональных величин. К этому типу нелинейности приводит, например, кинетика реакции, подчиняющейся уравнению Михаэлиса — Ментен, о чем свидетельствуют описанные примеры гликолиза [56, 9, 103], а также абстрактные модели Росслера, не включенные в примеры предыдущего раздела.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. КОЛЕБАНИЯ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 3. Колебательные реакции и их модели
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Периодические водные часы (реакция Бриггса—Раушера) [21]
- 3.3. Окисление малоновоб кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием (ППР) [7, 14, II, 47]
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций и их модели
- 3.11. Некаталитические реакции
- 3.12. Таблица колебательных реакций
- 4. Характеристики колебательных систем
- 4.2. Нелинейность систем
- 4.3. Параметры системы
- 4.4. Число решений
- 5. Глобальный анализ
- 5.2. Бифуркации как способ поиска колебаний
- 6. Классификация колебаний
- 6.2. Типы компонентов колебательных химических реакций
- 6.3. Типы колебательных математических решений
- 7. Состояние исследований и дальнейшие направления их развития
- Часть II. РАЗВИТИЕ ИССЛЕДОВАНИЙ ХИМИЧЕСКИХ КОЛЕБАНИЙ В ПОСЛЕДНЕЕ ВРЕМЯ
- 3. Реакции и модели, проявляющие колебания
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Колебательные йодные часы (реакция Бриггса—Раушера)
- 3.3. Окисление малоновой кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций
- 3.11. Некаталитические реакции
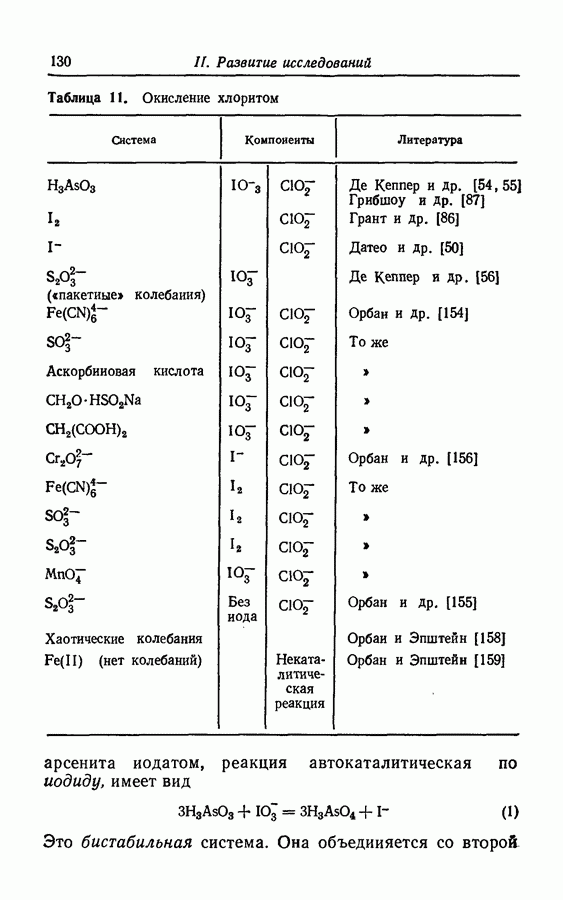
- 3.12. Окисление хлоритом
- 3.13. Разноплановые исследования
- 3.14. Общие модели и математические методы