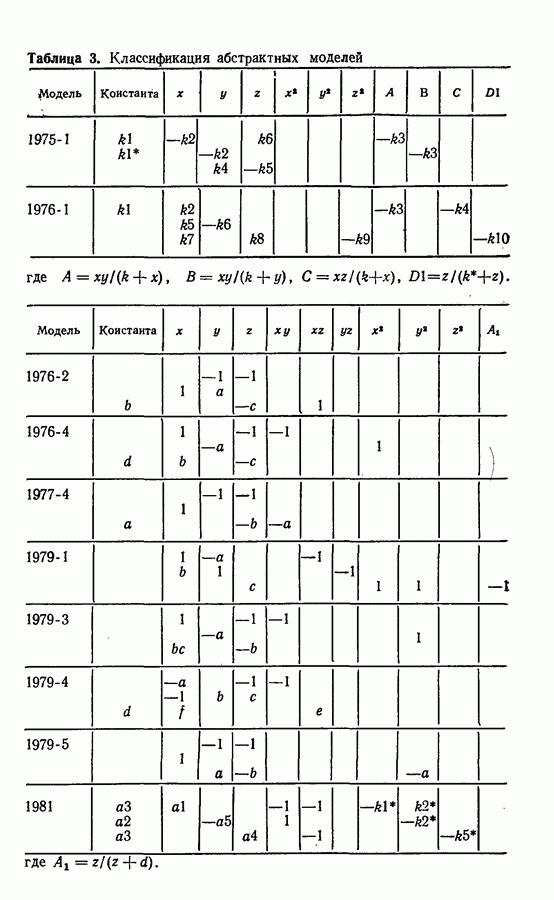
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.3. Типы колебательных математических решений
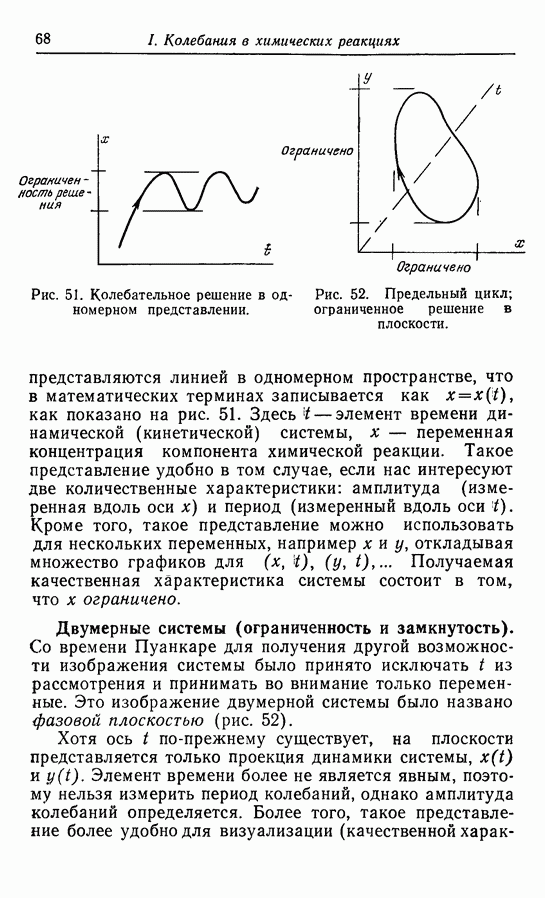
Колебания физико - химических параметров, таких, как температура, концентрации компонентов реакции и т. д., соответствуют колебательным решениям динамических уравнений (дифференциальных уравнений рассматриваемых систем). Как указывалось выше, различные реакции характеризуются различными типами колебательных математических решений. Хорошо известные предельные циклы впервые были исследованы и названы так Пуанкаре сто лет назад. Другие математические решения, хотя и были сформулированы в общем виде Пуанкаре, лишь недавно были исследованы и названы математиками. Так, аттракторы и точки взрыва в приложении к химическим реакциям были изучены намного позднее, чем предельные циклы.
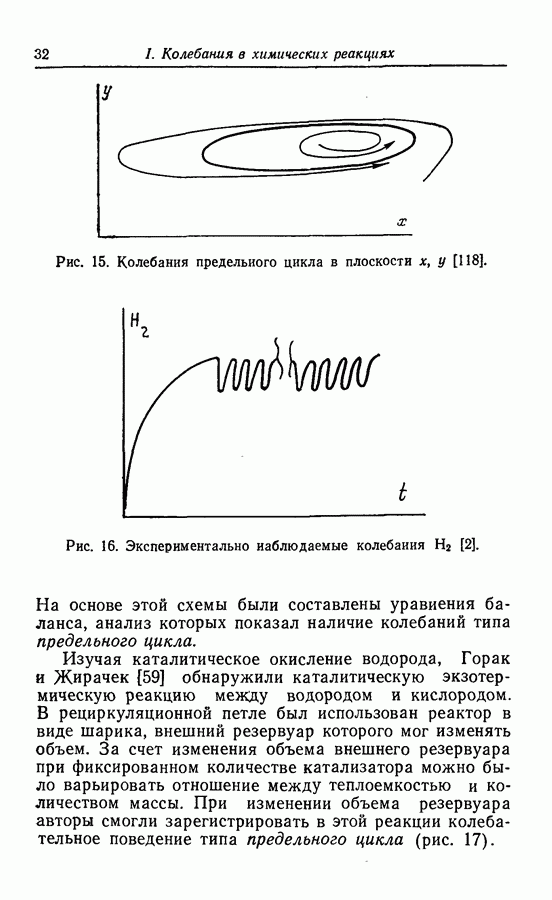
Предельный цикл. Предельный цикл, в частности для двумерных систем, представляет собой простейшую форму колебательных решений. Как указано в разд. 4.1, решения типа предельного цикла могут осуществляться в двумерных системах и системах с более высокой размерностью. Почти все примеры колебательных решений, описанных в литературе, относятся к типу предельного цикла. Таким примером простого предельного цикла может служить бимолекулярная модель Лефевра. Однако
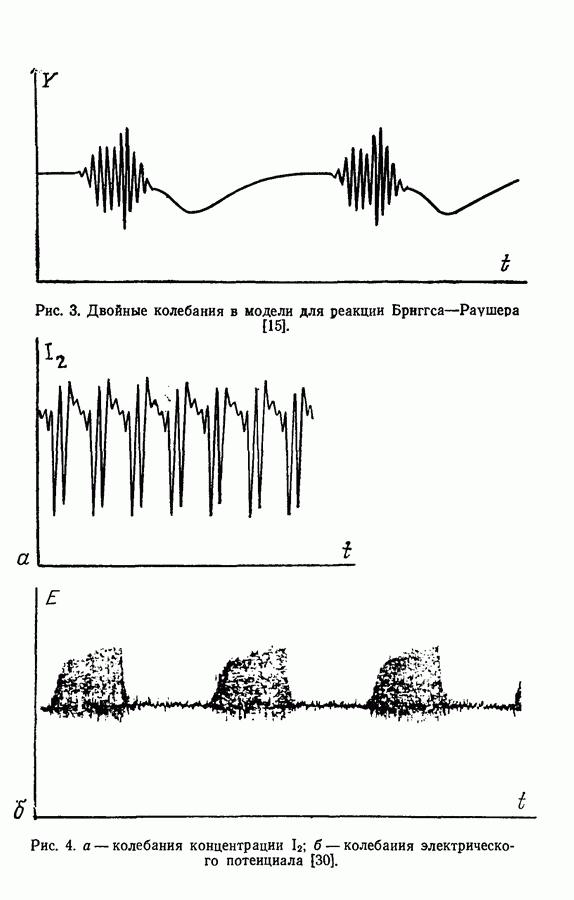
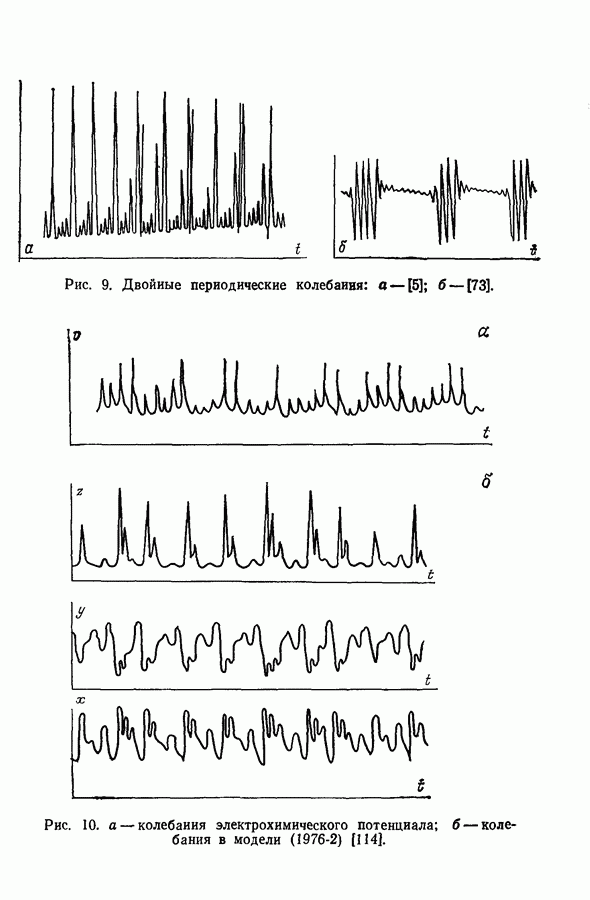
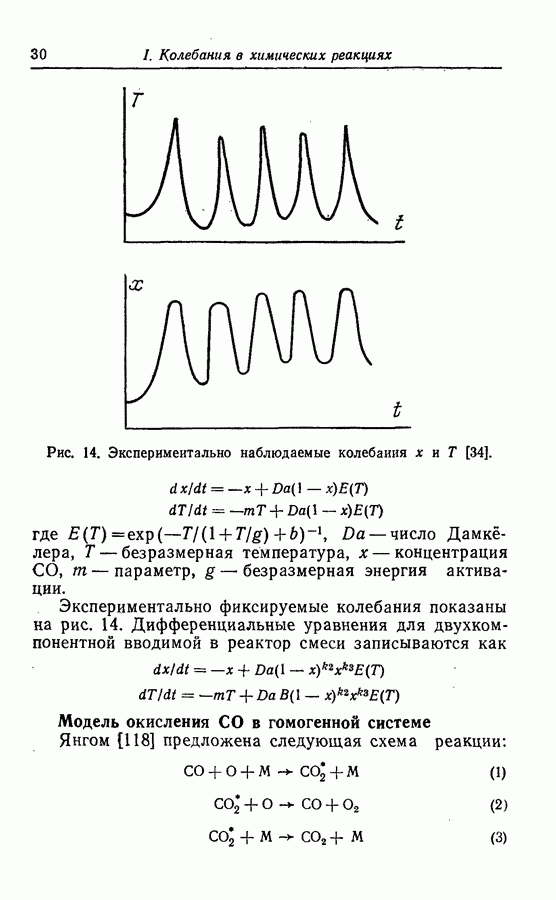
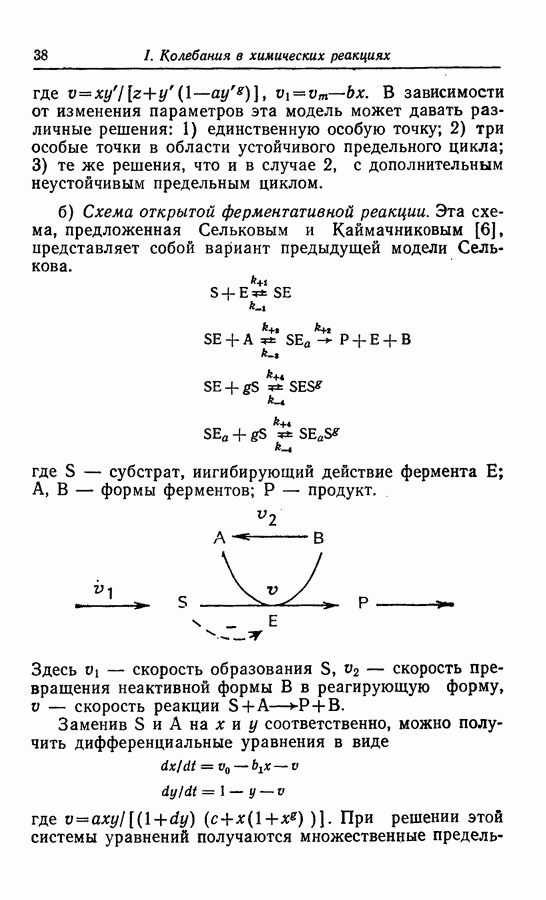
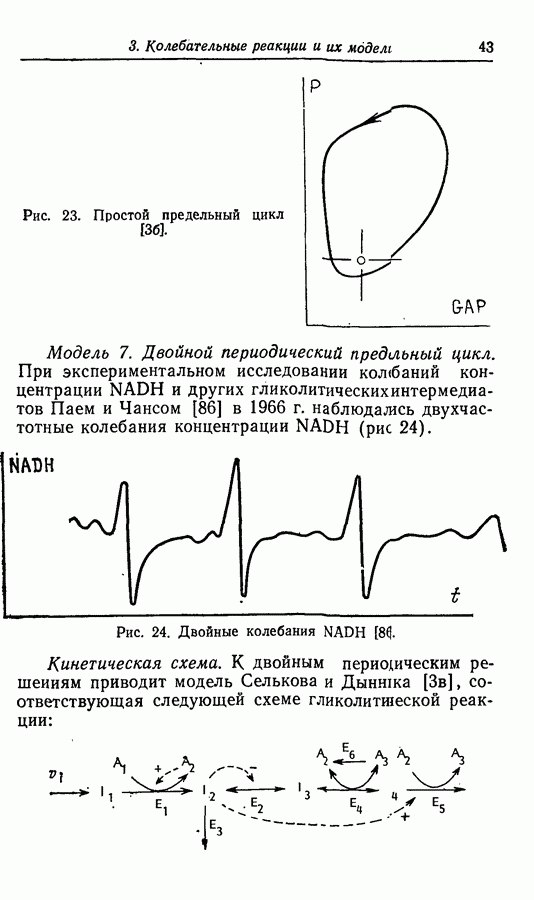
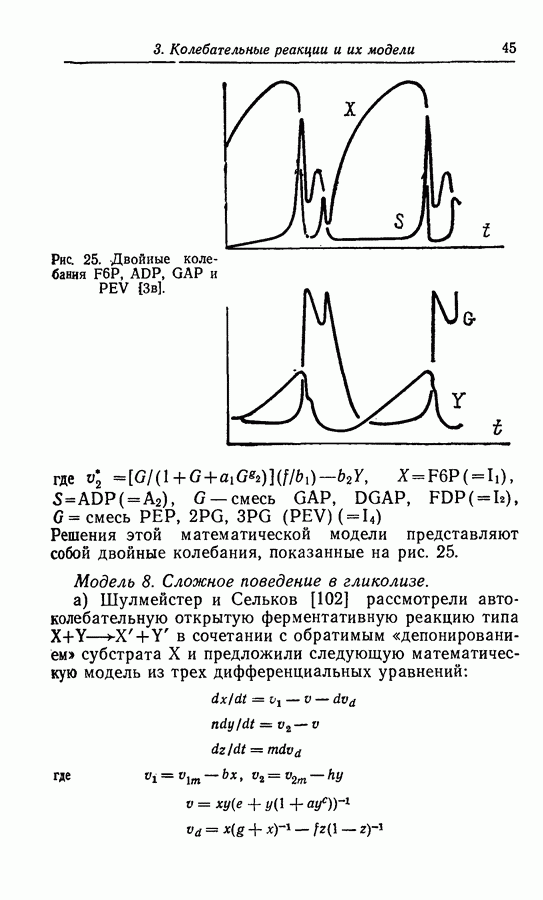
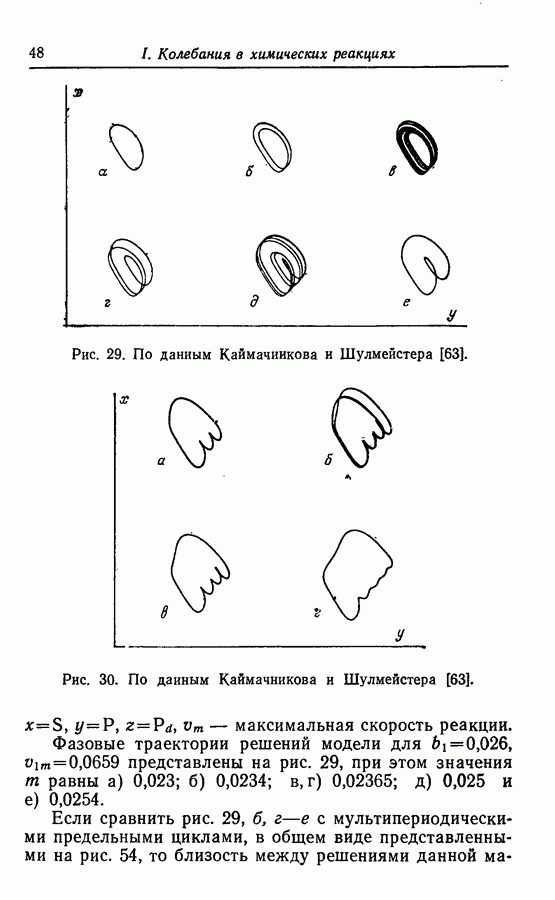
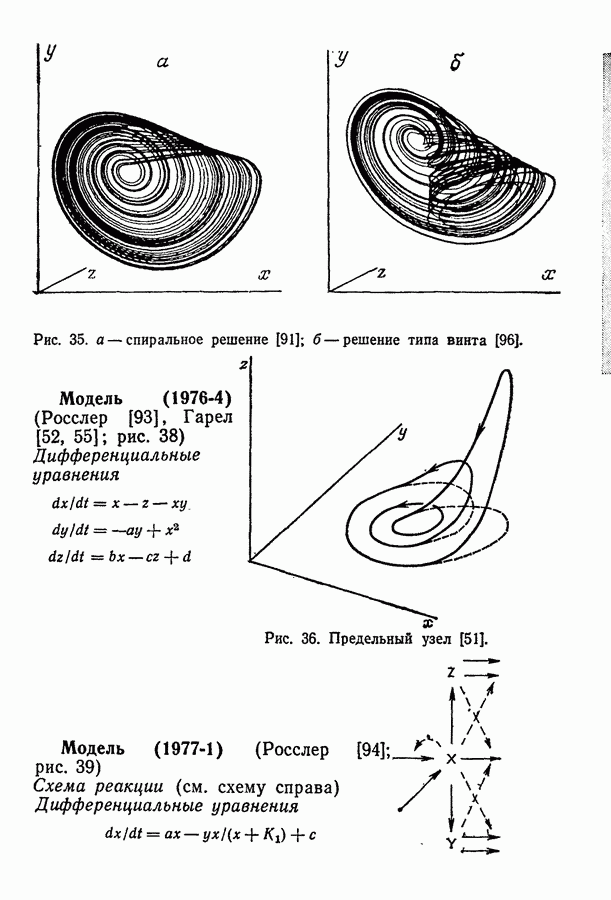
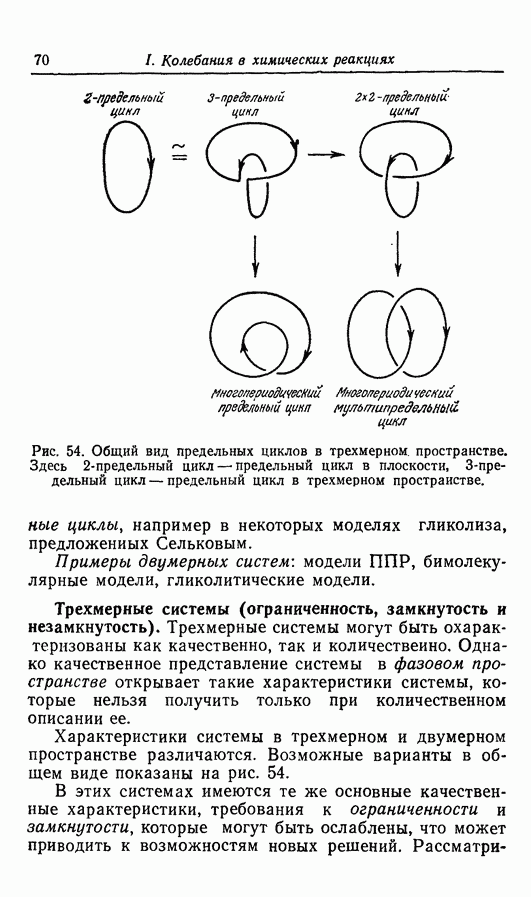
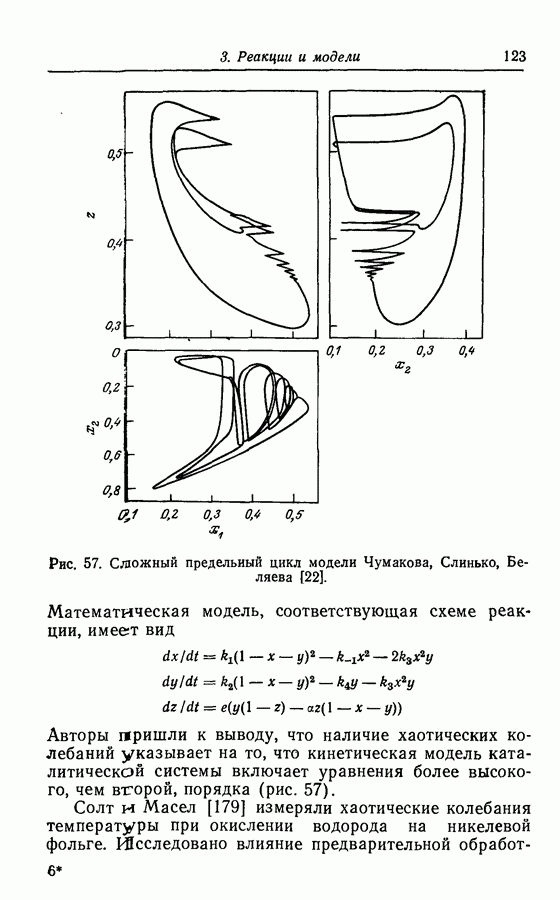
по мере увеличения размерностей системы не только могут появиться колебательные решения другого типа, но и решения типа предельного цикла становятся более сложными. В трехмерной системе, как показано выше в разд. 4.1, могут быть получены сложные предельные циклы, показанные в общем виде на рис. 54. В качестве возможных проекций предельного цикла характерного вида, представленного на рис. 54, могут служить «двойные колебания» в примерах Беша [13] (рис. 13), Марека и Свободовой [73], Вавилина с сотр. [113а] (рис. 9), Дынника и Селькова [36, в] (рис. 25) и Буассонада [15] (рис. 3 и 4).
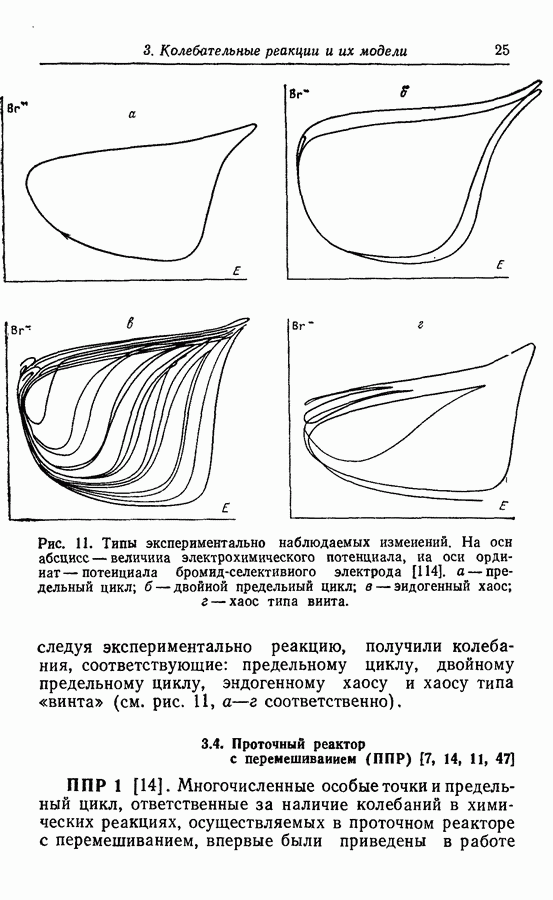
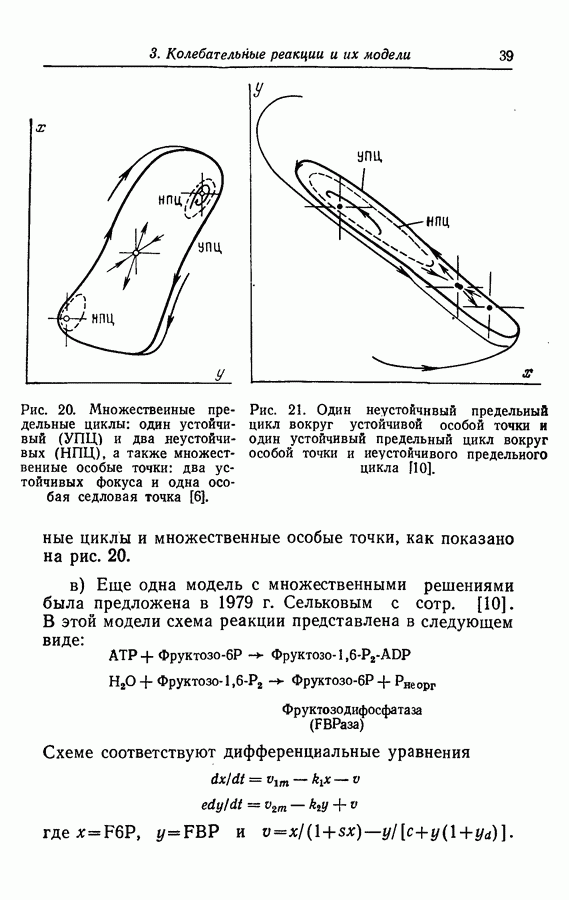
Предельный узел. Предельный узел, представленный на примере абстрактной модели (1976-2), является в общем виде также многопериодическим предельным циклом. Для абстрактной модели (1974-4) были также отмечены связанные предельные циклы. Эти связанные предельные циклы служат примерами характерного множественного предельного цикла, представленного на рис. 54.
Так как теоретические модели раскрывают возможности получения предельных циклов различной сложности, экспериментальные исследования зависят от того, насколько принимаются во внимание различные варианты предельных циклов.
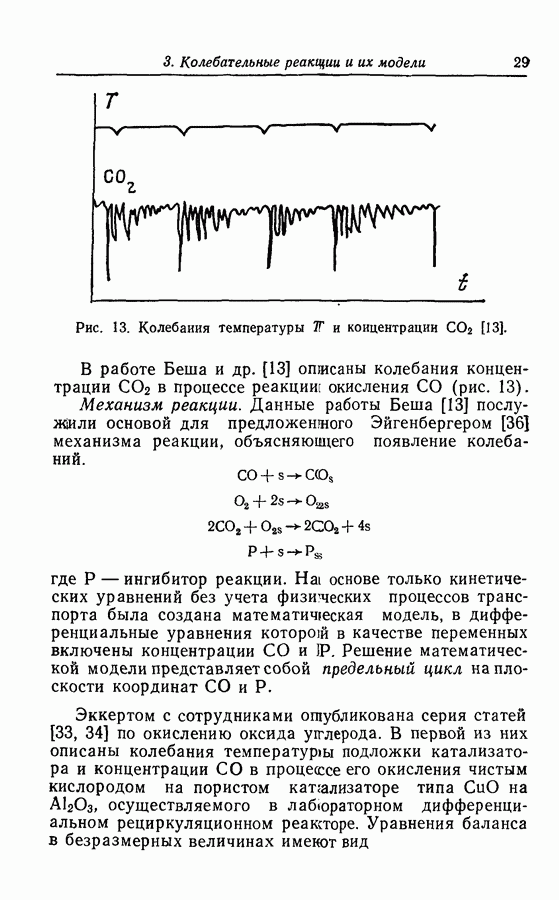
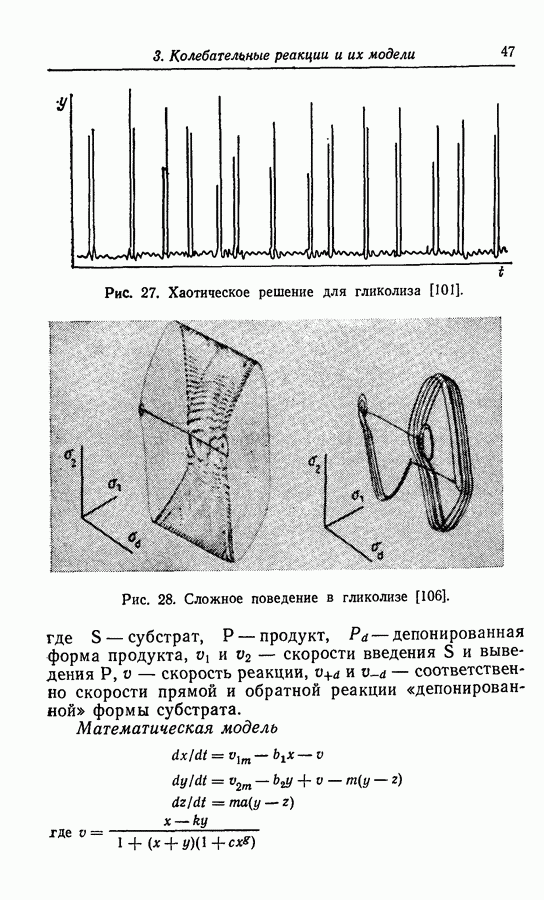
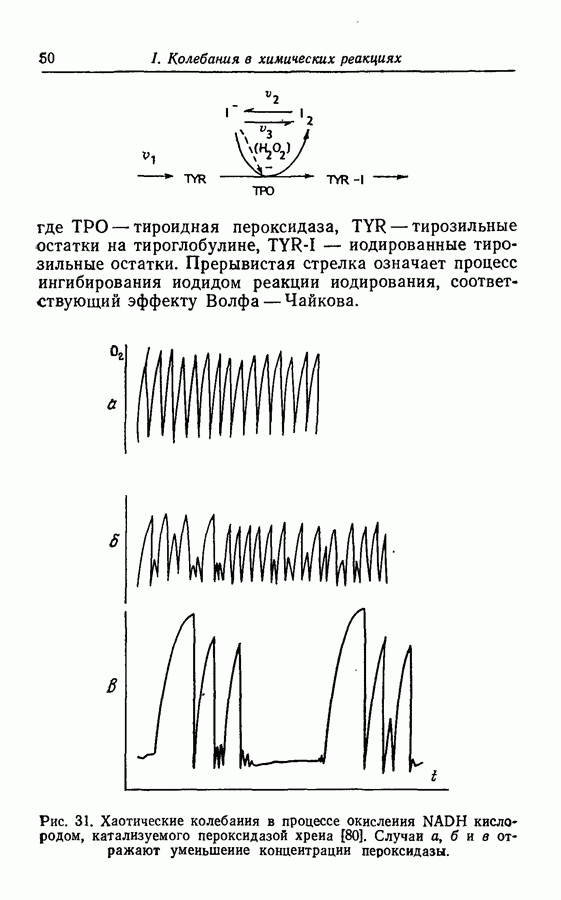
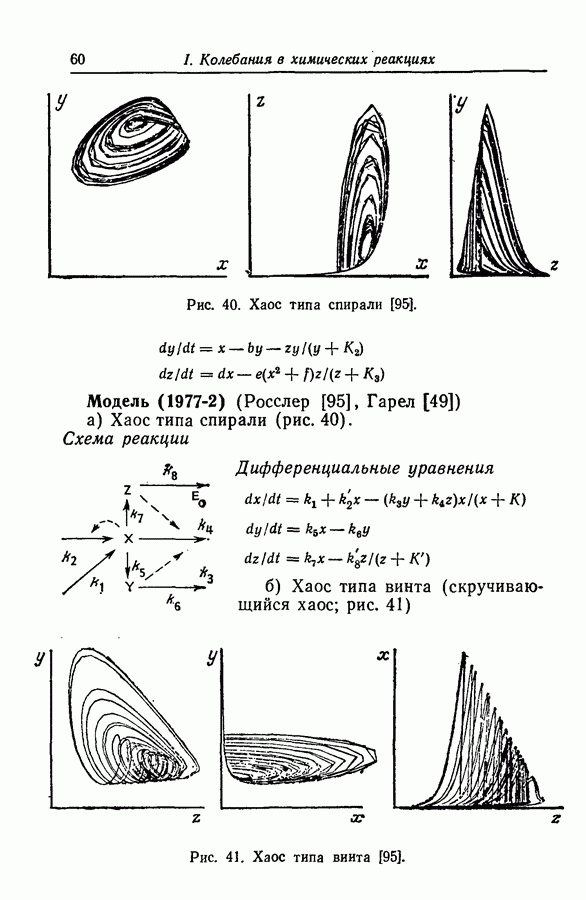
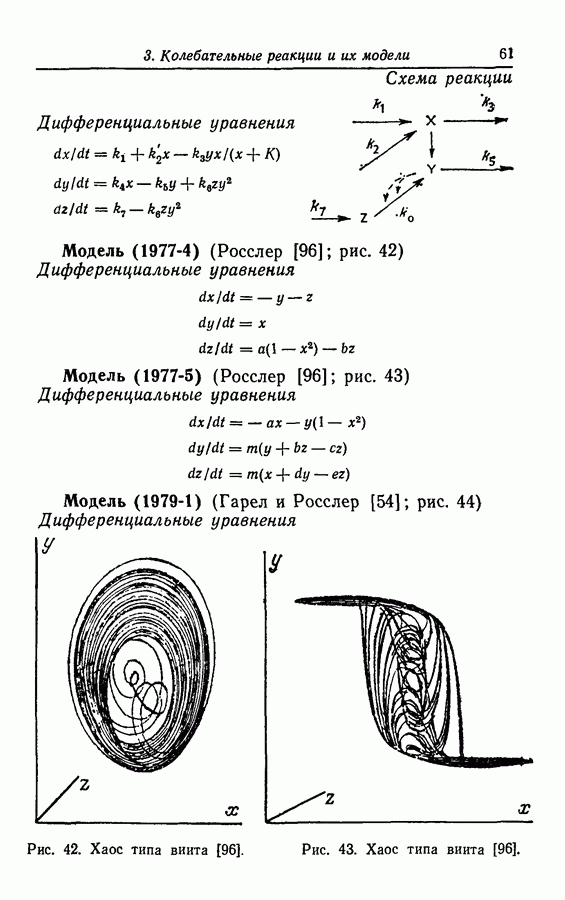
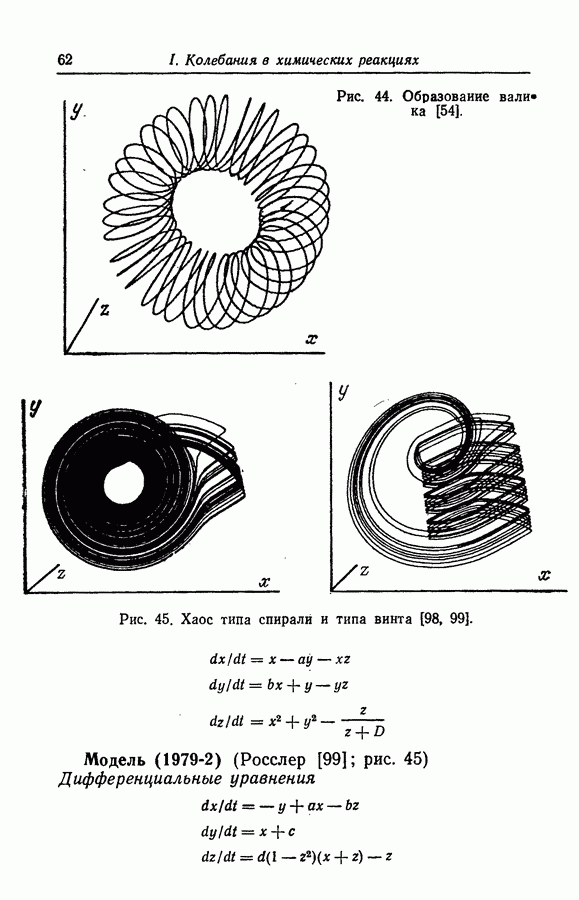
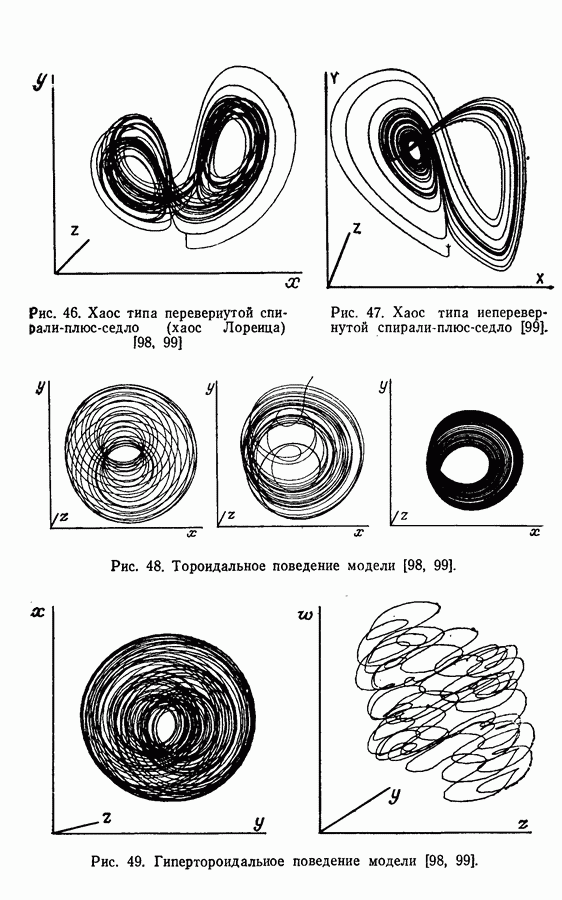
Аттракторы. Некоторые из колебательных решений, в частности найденные для абстрактных моделей Росслера, представляют собой аттракторы, более того, они хаотичны. Эти математические решения интересны тем, что, вероятно, многие экспериментально наблюдаемые колебания имеют ту же природу. Можно теоретически описать реакции, если изучать математические модели, правильно отражающие их поведение. Такие хаотические аттракторы проиллюстрированы примерами, приведенными в разд. 3.9.
Некоторые из хаотических колебаний получены при создании моделей с заданной геометрией. Примеры хаоса типа винта и тороидального хаоса в моделях (1977-3) и (1979-1,2) получены при химической реализации колебаний типа спирали, предложенных Гарелом [49].
Используя противоположный подход, заключающийся в том, что постановка эксперимента производится на основании решения математической модели, Олсен и Дегн [80] показали, что абстрактные модели могут привести к пониманию колебательных химических реакций, для которых характерны не только колебания типа предельного цикла, но и хаотические колебания типа аттрактора.
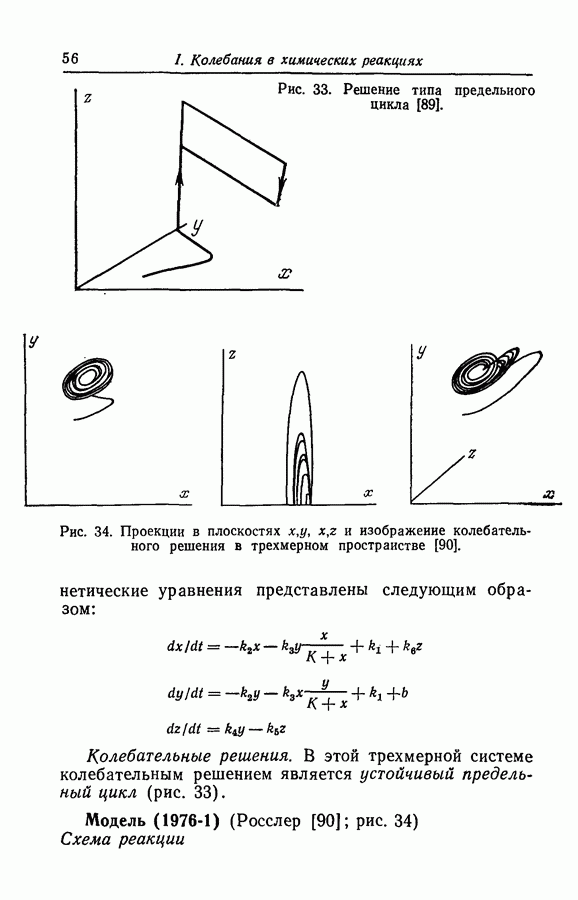
Точка взрыва. Как уже было показано, наблюдающиеся в некоторых реакциях колебания не моделируются в виде периодического предельного цикла; фактически на протяжении длительного в разумных пределах интервала времени в этих системах нельзя определить период. Математические решения, не включающие период, могут быть получены для трехмерных математических моделей, например для модели (1976-4). Это решение было названо в общем виде точкой взрыва (Гарел [55]).
Вполне очевидно, что могут быть многочисленные примеры химических реакций, колебания в которых не имеют определенного периода; следовательно, такие реакции могут соответствовать моделям с решением типа точки взрыва. Однако эти утверждения остаются недоказанными.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. КОЛЕБАНИЯ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 3. Колебательные реакции и их модели
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Периодические водные часы (реакция Бриггса—Раушера) [21]
- 3.3. Окисление малоновоб кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием (ППР) [7, 14, II, 47]
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций и их модели
- 3.11. Некаталитические реакции
- 3.12. Таблица колебательных реакций
- 4. Характеристики колебательных систем
- 4.2. Нелинейность систем
- 4.3. Параметры системы
- 4.4. Число решений
- 5. Глобальный анализ
- 5.2. Бифуркации как способ поиска колебаний
- 6. Классификация колебаний
- 6.2. Типы компонентов колебательных химических реакций
- 6.3. Типы колебательных математических решений
- 7. Состояние исследований и дальнейшие направления их развития
- Часть II. РАЗВИТИЕ ИССЛЕДОВАНИЙ ХИМИЧЕСКИХ КОЛЕБАНИЙ В ПОСЛЕДНЕЕ ВРЕМЯ
- 3. Реакции и модели, проявляющие колебания
- 3.1. Разложение пероксида водорода, катализируемое иодатом (реакция Брея—Либавски)
- 3.2. Колебательные йодные часы (реакция Бриггса—Раушера)
- 3.3. Окисление малоновой кислоты броматом (реакция Белоусова—Жаботинского)
- 3.4. Проточный реактор с перемешиванием
- 3.5. Реакции на твердых катализаторах
- 3.6. Колебания в гликолизе
- 3.7. Реакции, катализируемые пероксидазой
- 3.8. Разложение дитионита натрия
- 3.9. Бимолекулярная модель
- 3.10. Абстрактные системы реакций
- 3.11. Некаталитические реакции
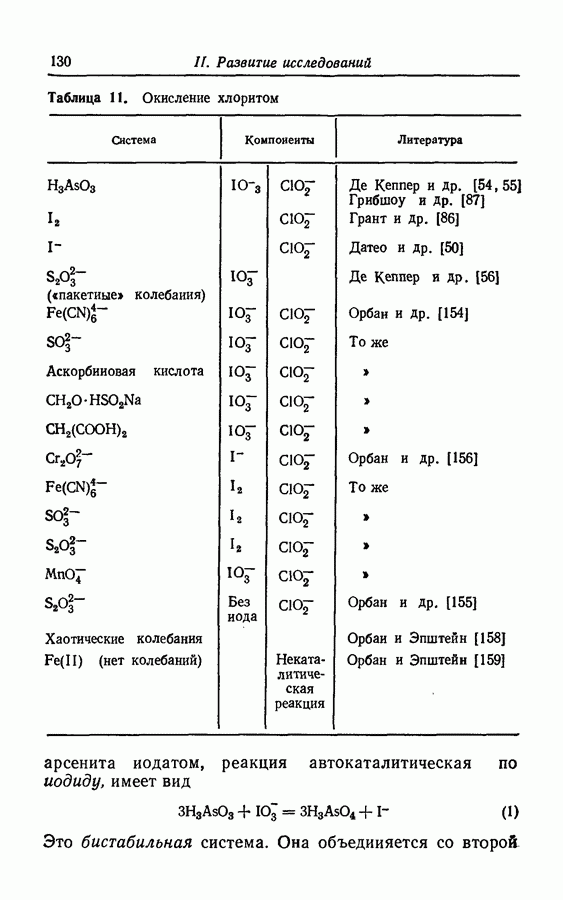
- 3.12. Окисление хлоритом
- 3.13. Разноплановые исследования
- 3.14. Общие модели и математические методы