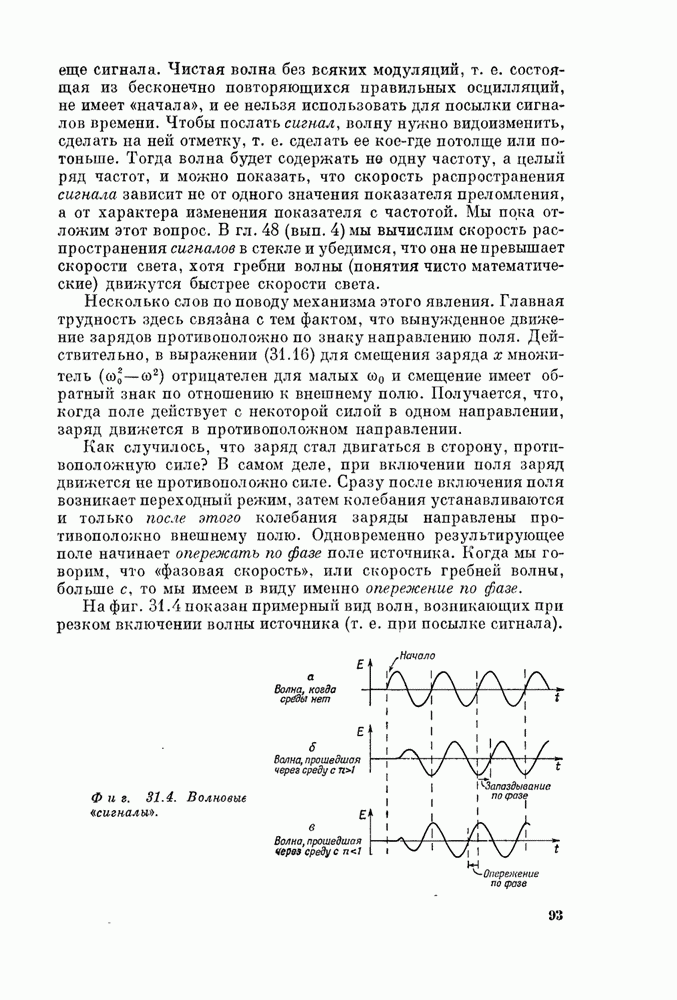
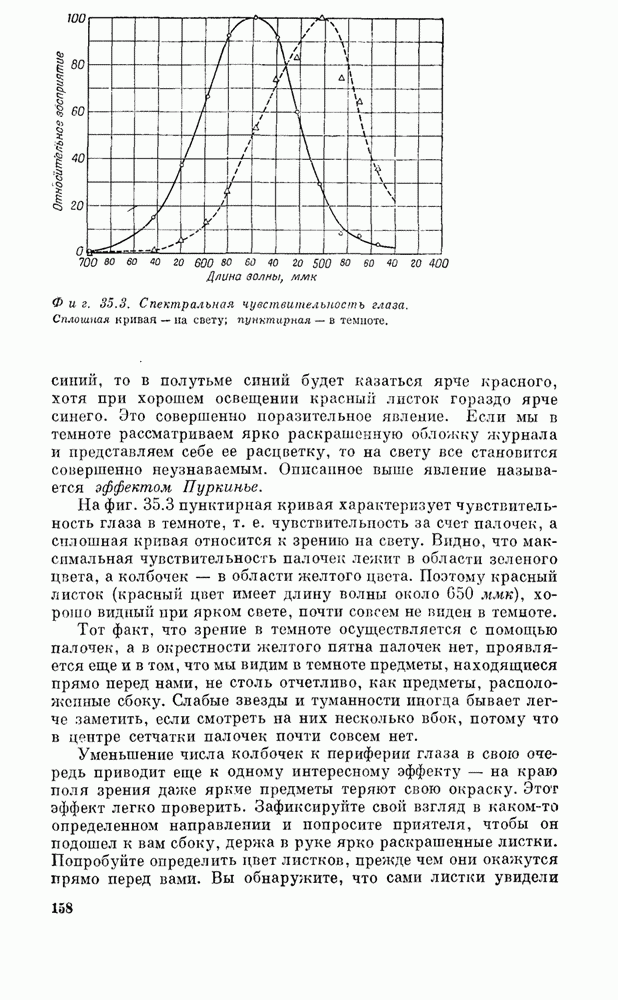
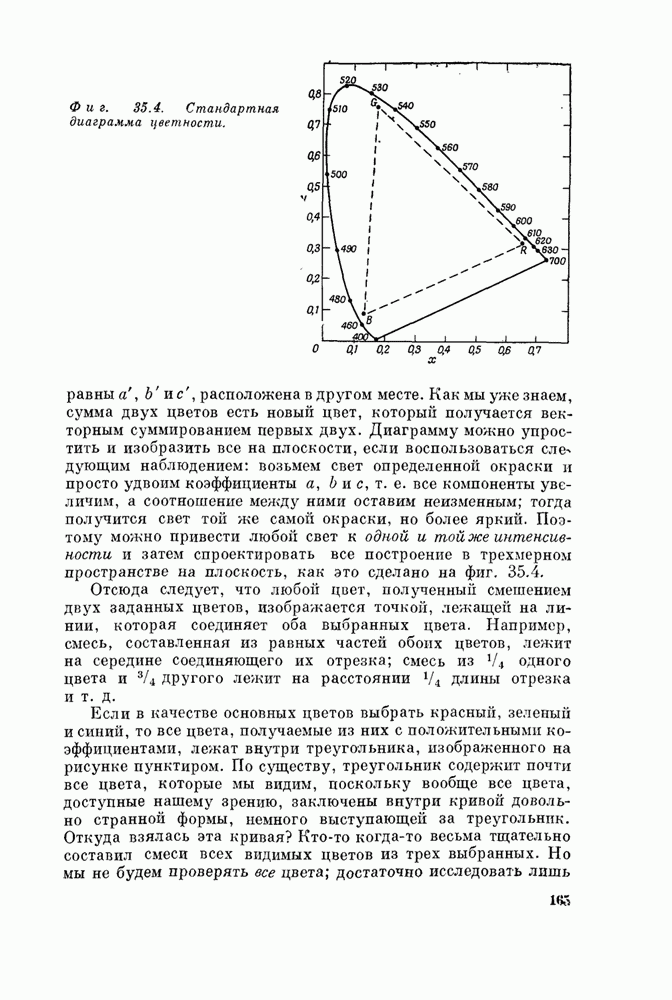
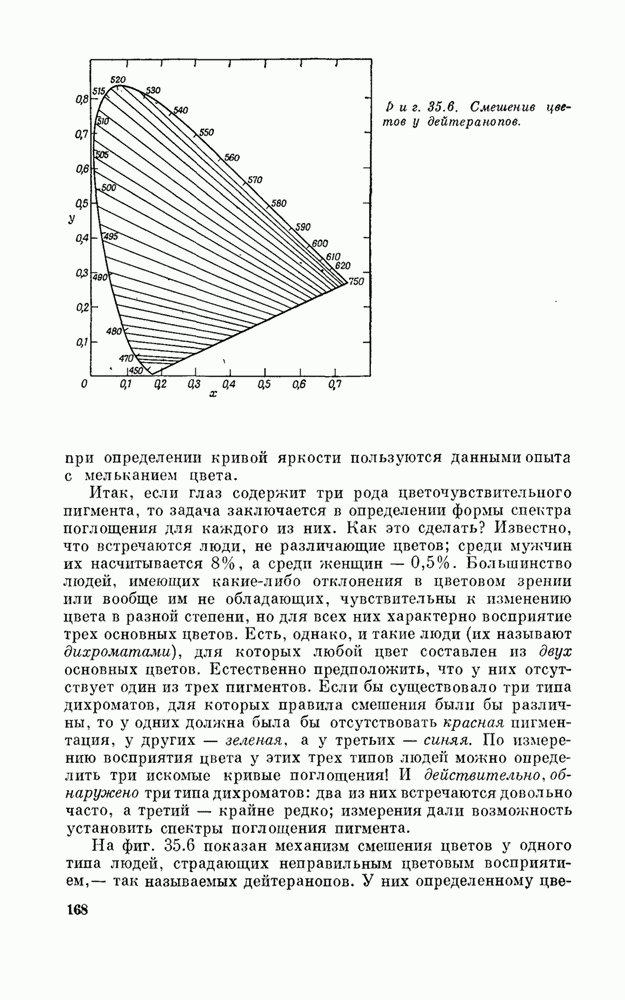
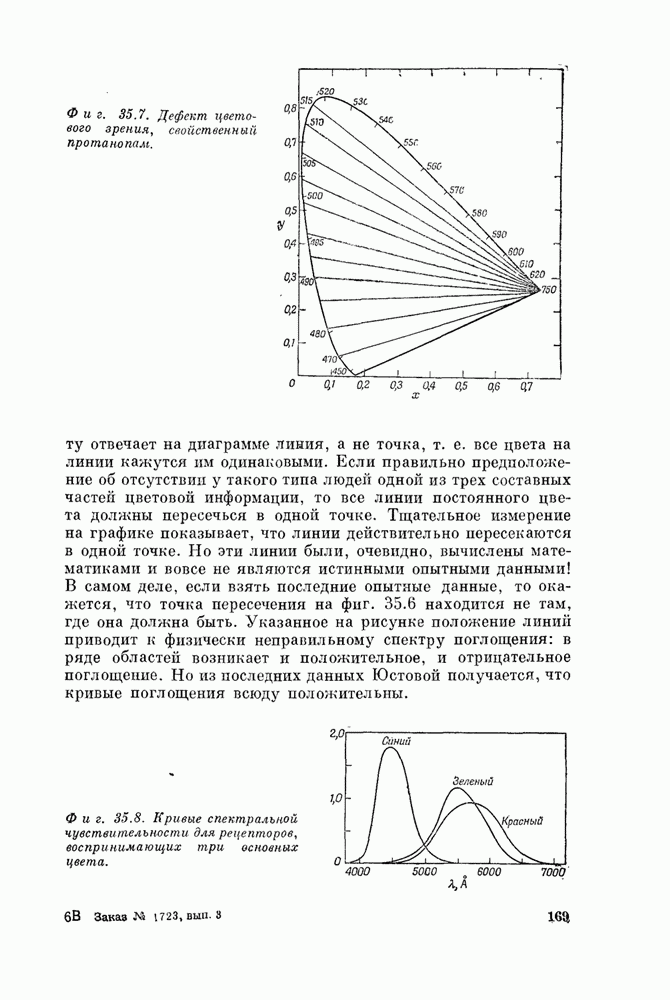
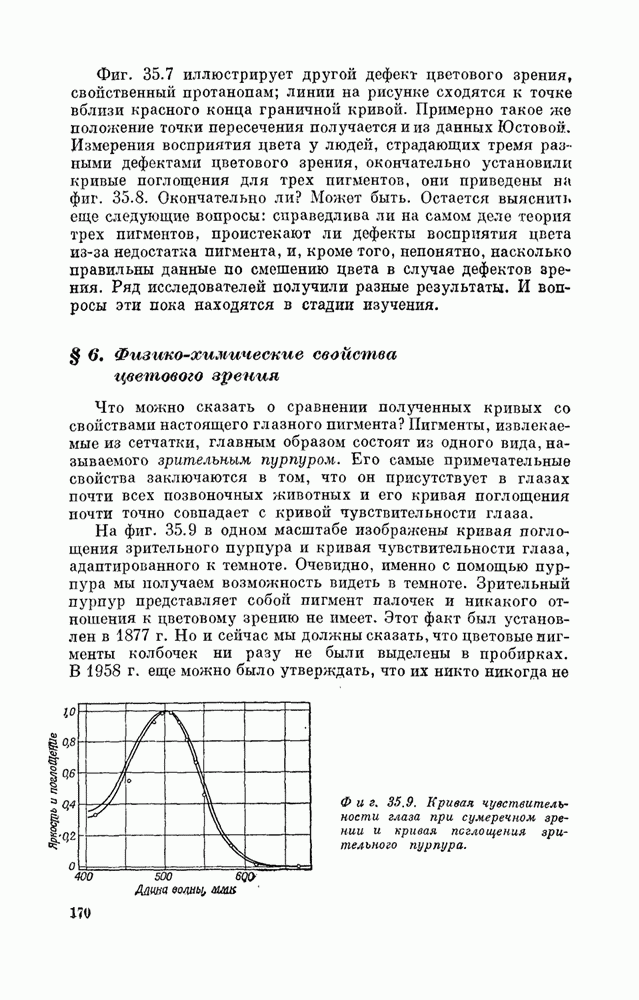
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 30. Дифракция
§ 1. Результирующее поле n одинаковых осцилляторов
Настоящая глава — непосредственное продолжение предыдущей, хотя название «Интерференция» здесь заменено словом «Дифракция». До сих пор никому не удалось удовлетворительным образом определить разницу между дифракцией и интерференцией. Дело здесь только в привычке, а существенного физического различия между этими явлениями нот. Единственное, что можно сказать по этому поводу, — это следующее: когда источников мало, например два, то результат их совместного действия обычно называют интерференцией, а если источников много, то чаще говорят о дифракции. Поэтому мы не будем утруждать себя вопросом — интерференция это или дифракция, а просто продолжим наше обсуждение с того места, где мы остановились в предыдущей главе.
Обсудим теперь случай,
когда имеется ![]() осцилляторов,
расположенных на равных расстояниях один от другого и обладающих равными
амплитудами, но разными фазами создаваемых ими полей. Разность фаз создается
либо из-за выбора определенных фазовых сдвигов колебаний осцилляторов, либо
потому, что мы находимся под углом к осцилляторам и возникает разность хода
лучей. Независимо от причины возникновения разности фаз необходимо вычислить сумму
такого вида:
осцилляторов,
расположенных на равных расстояниях один от другого и обладающих равными
амплитудами, но разными фазами создаваемых ими полей. Разность фаз создается
либо из-за выбора определенных фазовых сдвигов колебаний осцилляторов, либо
потому, что мы находимся под углом к осцилляторам и возникает разность хода
лучей. Независимо от причины возникновения разности фаз необходимо вычислить сумму
такого вида:
![]() , (30.1)
, (30.1)
где ![]() — разность фаз соседних
осцилляторов для некоторого направления лучей. В данном частном случае
— разность фаз соседних
осцилляторов для некоторого направления лучей. В данном частном случае ![]() . Вычислим сумму
. Вычислим сумму ![]() . Для этого
воспользуемся геометрическим способом сложения. Длина первого слагаемого
. Для этого
воспользуемся геометрическим способом сложения. Длина первого слагаемого ![]() , а его фаза равна
нулю; длина второго также
, а его фаза равна
нулю; длина второго также ![]() , а фаза его равна
, а фаза его равна ![]() . Следующее
слагаемое имеет снова длину
. Следующее
слагаемое имеет снова длину ![]() и фазу, равную
и фазу, равную ![]() , и т. д. В конце концов
получается часть правильного многоугольника с
, и т. д. В конце концов
получается часть правильного многоугольника с ![]() сторонами (фиг. 30.1).
сторонами (фиг. 30.1).

Фигура. 30.1. Результирующая амплитуда шести эквидистантных
источников при разности фаз ![]() между каждыми двумя соседними
источниками.
между каждыми двумя соседними
источниками.
Вершины многоугольника
лежат, конечно, на окружности, и чтобы легче было определить результирующую
амплитуду, найдем радиус этой окружности. Пусть ![]() есть ее центр. Тогда угол
есть ее центр. Тогда угол ![]() равен как раз
фазе
равен как раз
фазе ![]() (поскольку
радиус
(поскольку
радиус ![]() образует
с
образует
с ![]() такой
же угол, как
такой
же угол, как ![]() с
с
![]() ).
Следовательно, радиус
).
Следовательно, радиус ![]() должен удовлетворять равенству
должен удовлетворять равенству ![]() , откуда мы и
находим величину
, откуда мы и
находим величину ![]() . Далее, большой угол
. Далее, большой угол ![]() равен
равен ![]() следовательно,
следовательно, ![]() . Исключая из
обоих равенств
. Исключая из
обоих равенств ![]() ,
получаем
,
получаем
![]() (30.2)
(30.2)
Таким образом, суммарная интенсивность оказывается равной
 . (30.3)
. (30.3)
Проанализируем это выражение
и обсудим вытекающие из него следствия. Прежде всего, положив ![]() , получим, как и
следовало ожидать,
, получим, как и
следовало ожидать, ![]() . Проверим формулу для
. Проверим формулу для ![]() : с помощью
соотношения
: с помощью
соотношения ![]() сразу
находим
сразу
находим ![]() ,
что совпадает с (29.12).
,
что совпадает с (29.12).
Мы вынуждены
рассматривать сложение полей от многих источников потому, что в этом случае
интенсивность в одном направлении получается много больше, чем в соседних, т.
е. все побочные максимумы интенсивности оказываются гораздо меньше основного.
Чтобы понять этот факт, начертим кривую соответствующую выражению (30.3) для
больших ![]() и
и
![]() , близких
к нулю. Прежде всего, когда
, близких
к нулю. Прежде всего, когда ![]() точно равно нулю, мы получаем
отношение 0/0, но фактически для бесконечно малых
точно равно нулю, мы получаем
отношение 0/0, но фактически для бесконечно малых ![]() отношение синусов равно
отношение синусов равно ![]() , так как синус
можно заменить его аргументом. Таким образом, максимум кривой в
, так как синус
можно заменить его аргументом. Таким образом, максимум кривой в ![]() раз больше
интенсивности одного осциллятора. Этот результат легко понять, поскольку при
нулевой разности фаз все
раз больше
интенсивности одного осциллятора. Этот результат легко понять, поскольку при
нулевой разности фаз все ![]() маленьких векторов складываются в
один вектор, в
маленьких векторов складываются в
один вектор, в ![]() раз
больший исходного, а интенсивность увеличивается в
раз
больший исходного, а интенсивность увеличивается в ![]() раз.
раз.
С ростом фазы ![]() отношение двух
синусов падает и обращается в нуль в первый раз при
отношение двух
синусов падает и обращается в нуль в первый раз при ![]() , поскольку
, поскольку ![]() . Другими словами,
значение
. Другими словами,
значение ![]() отвечает
первому минимуму кривой (фиг. 30.2). С точки зрения векторов на фиг. 30.1
первый минимум возникает в том случае, когда стрелки векторов возвращаются в
исходную точку, при этом полная разность фаз от первого до последнего
осциллятора равна
отвечает
первому минимуму кривой (фиг. 30.2). С точки зрения векторов на фиг. 30.1
первый минимум возникает в том случае, когда стрелки векторов возвращаются в
исходную точку, при этом полная разность фаз от первого до последнего
осциллятора равна ![]() .
.
Перейдем к следующему максимуму
и покажем, что он действительно, как мы и ждали, много меньше первого. Для точного
определения положения максимума необходимо учитывать, что и числитель, и
знаменатель я (30.3) оба меняются с изменением ![]() . Мы не станем этого делать,
поскольку при большом
. Мы не станем этого делать,
поскольку при большом ![]() меняется медленнее
меняется медленнее ![]() и условие
и условие ![]() дает положение
максимума с большой точностью. Максимум
дает положение
максимума с большой точностью. Максимум ![]() достигается при
достигается при ![]() или
или ![]() . Это означает, что стрелки
векторов описывают полторы окружности.
. Это означает, что стрелки
векторов описывают полторы окружности.
Подставляя ![]() , получаем
, получаем ![]() в числителе
(30.3) (с этой целью и был выбран угол
в числителе
(30.3) (с этой целью и был выбран угол ![]() ) и
) и ![]() в знаменателе. Для достаточно
большого
в знаменателе. Для достаточно
большого ![]() можно
заменить синус его аргументом:
можно
заменить синус его аргументом: ![]() . Отсюда интенсивность во втором
максимуме оказывается равной
. Отсюда интенсивность во втором
максимуме оказывается равной ![]() / =70 (4ге79л2). Но
/ =70 (4ге79л2). Но ![]() — не что иное,
как интенсивность в первом максимуме, т. е. интенсивность второго максимума
получается равной
— не что иное,
как интенсивность в первом максимуме, т. е. интенсивность второго максимума
получается равной ![]() от максимальной, что составляет
0,047, или меньше 5%! Остальные максимумы, очевидно, будут еще меньше. Таким
образом, возникает очень узкий основной максимум и очень слабые дополнительные
максимумы по обе стороны от основного.
от максимальной, что составляет
0,047, или меньше 5%! Остальные максимумы, очевидно, будут еще меньше. Таким
образом, возникает очень узкий основной максимум и очень слабые дополнительные
максимумы по обе стороны от основного.

Фигура 30.2. Зависимость интенсивности от фазового угла для большого числа осцилляторов с одинаковыми амплитудами.

Фигура 30.3. Устройство из ![]() одинаковых осцилляторов, расположенных
на линии. Фаза колебания
одинаковых осцилляторов, расположенных
на линии. Фаза колебания ![]() -го осциллятора
-го осциллятора ![]()
Можно показать, что
площадь под кривой интенсивности, включая все максимумы, равна ![]() и в два раза
превышает площадь пунктирного прямоугольника на фиг. 30.2.
и в два раза
превышает площадь пунктирного прямоугольника на фиг. 30.2.
Посмотрим теперь, что
дает формула (30.3) в приложении к разным случаям. Пусть источники расположены
на одной линии, как показано на фиг. 30.3. Всего имеется ![]() источников на расстоянии
источников на расстоянии ![]() друг от друга, и
сдвиг фазы между соседними источниками выбран равным
друг от друга, и
сдвиг фазы между соседними источниками выбран равным ![]() . Тогда для лучей,
распространяющихся в заданном направлении
. Тогда для лучей,
распространяющихся в заданном направлении ![]() , отсчитываемом от нормали, вследствие
разности хода лучей от двух соседних источников возникает дополнительный сдвиг
фазы
, отсчитываемом от нормали, вследствие
разности хода лучей от двух соседних источников возникает дополнительный сдвиг
фазы ![]() .
Таким образом,
.
Таким образом,
![]() . (30.4)
. (30.4)
Рассмотрим сначала случай
![]() . Все
осцилляторы колеблются с одной фазой; требуется найти интенсивность их излучения
как функцию угла
. Все
осцилляторы колеблются с одной фазой; требуется найти интенсивность их излучения
как функцию угла ![]() . Подставим с этой целью
. Подставим с этой целью ![]() в формулу (30.3)
и посмотрим, что получится в результате. Прежде всего при
в формулу (30.3)
и посмотрим, что получится в результате. Прежде всего при ![]() возникает максимум.
Значит, осцилляторы, колеблющиеся с одной фазой, дают мощное излучение в
направлении
возникает максимум.
Значит, осцилляторы, колеблющиеся с одной фазой, дают мощное излучение в
направлении ![]() .
Интересно узнать, где находится первый минимум.
.
Интересно узнать, где находится первый минимум.
Он возникает при ![]() ; другими словами,
первый минимум кривой интенсивности определяется из соотношения
; другими словами,
первый минимум кривой интенсивности определяется из соотношения ![]() . Сокращая на
. Сокращая на ![]() , получаем
, получаем
![]() . (30.5)
. (30.5)
Теперь разберем с
физической точки зрения, почему минимум возникает именно в этом месте. В этом
выражении ![]() есть
полная длина
есть
полная длина ![]() нашей
системы осцилляторов. Обращаясь к фиг. 30.3, мы видим, что
нашей
системы осцилляторов. Обращаясь к фиг. 30.3, мы видим, что ![]() . Формула (30.5)
подсказывает нам, что минимум возникает при
. Формула (30.5)
подсказывает нам, что минимум возникает при ![]() , равном одной длине волны. Но почему
минимум получается при
, равном одной длине волны. Но почему
минимум получается при ![]() ? Дело в том, что поля от отдельных
осцилляторов равномерно распределены по фазе от 0 до 360°. Стрелки (см. фиг.
30.1) описывают полную окружность; мы складываем равные векторы, имеющие
произвольные направления, а в этом случае сумма равна нулю. Вот при таких
значениях угла, когда
? Дело в том, что поля от отдельных
осцилляторов равномерно распределены по фазе от 0 до 360°. Стрелки (см. фиг.
30.1) описывают полную окружность; мы складываем равные векторы, имеющие
произвольные направления, а в этом случае сумма равна нулю. Вот при таких
значениях угла, когда ![]() , возникает минимум. Это и есть
первый минимум.
, возникает минимум. Это и есть
первый минимум.
Формула (30.3) имеет еще
одну важную особенность: при увеличении угла ![]() на число, кратное
на число, кратное ![]() , значение
интенсивности не меняется. Поэтому для
, значение
интенсивности не меняется. Поэтому для ![]() и т. д. также возникают резкие и
высокие максимумы. Вблизи этих максимумов интенсивность повторяет свой ход (см.
фиг. 30.2). Зададимся вопросом, в силу каких геометрических соотношений
возникают другие максимумы? Условие появления максимума записывается в виде
и т. д. также возникают резкие и
высокие максимумы. Вблизи этих максимумов интенсивность повторяет свой ход (см.
фиг. 30.2). Зададимся вопросом, в силу каких геометрических соотношений
возникают другие максимумы? Условие появления максимума записывается в виде ![]() , где
, где ![]() — любое целое
число. Отсюда получаем
— любое целое
число. Отсюда получаем ![]() . Сокращая на
. Сокращая на ![]() , получаем
, получаем
![]() . (30.6)
. (30.6)
Это соотношение очень
похоже на формулу (30.5). Однако там было ![]() . Разница в том, что здесь нужно
взять каждый отдельный источник и выяснить, что для него означает условие
. Разница в том, что здесь нужно
взять каждый отдельный источник и выяснить, что для него означает условие ![]() ; угол
; угол ![]() здесь таков, что
разность хода
здесь таков, что
разность хода ![]() .
Другими словами, волны, идущие от источников, различаются по фазе на величину,
кратную 360°, и, следовательно, все находятся в фазе. Поэтому при сложении волн
возникает столь же высокий максимум, как и в рассмотренном ранее случае
.
Другими словами, волны, идущие от источников, различаются по фазе на величину,
кратную 360°, и, следовательно, все находятся в фазе. Поэтому при сложении волн
возникает столь же высокий максимум, как и в рассмотренном ранее случае ![]() . Побочные
максимумы и весь ход интенсивности здесь такие же, как в случае
. Побочные
максимумы и весь ход интенсивности здесь такие же, как в случае ![]() . Таким образом,
наша система посылает пучки лучей в разных направлениях, причем каждый пучок
имеет высокий центральный максимум и ряд слабых боковых. Главные (центральные) максимумы
в зависимости от величины
. Таким образом,
наша система посылает пучки лучей в разных направлениях, причем каждый пучок
имеет высокий центральный максимум и ряд слабых боковых. Главные (центральные) максимумы
в зависимости от величины ![]() называются максимумами нулевого,
первого и т. д. порядков;
называются максимумами нулевого,
первого и т. д. порядков; ![]() называют порядком максимума.
называют порядком максимума.
Обратите внимание на
такой факт: если ![]() меньше
меньше ![]() , то формула (30.6) имеет
единственное решение при
, то формула (30.6) имеет
единственное решение при ![]() . Поэтому для малого расстояния между
источниками возникает один-единственный пучок, сконцентрированный около
. Поэтому для малого расстояния между
источниками возникает один-единственный пучок, сконцентрированный около ![]() . (Разумеется,
есть еще пучок в обратном направлении.) Чтобы получить максимумы других
порядков, расстояние
. (Разумеется,
есть еще пучок в обратном направлении.) Чтобы получить максимумы других
порядков, расстояние ![]() должно быть больше одной длины волны.
должно быть больше одной длины волны.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
- § 4. Диаграмма цветности
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии