| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Измерение восприятия цвета
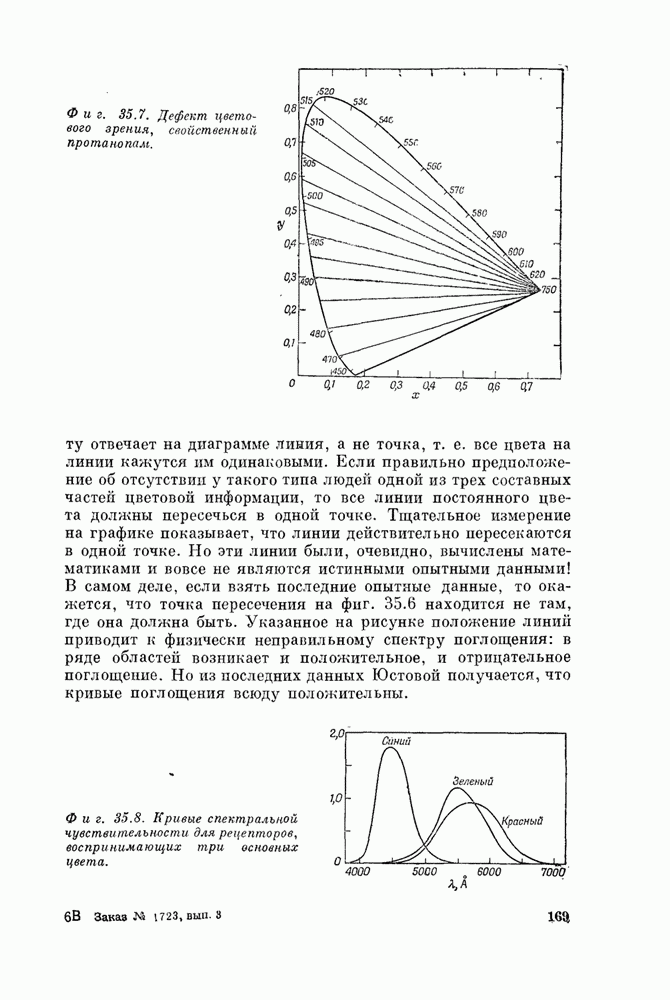
Теперь мы займемся зрением, осуществляемым с помощью колбочек, т. е. зрением при ярком освещении. Самое главное и самое характерное свойство такого зрения — это цвет. Мы уже знаем, что белый свет с помощью призмы можно разложить на целый спектр лучей с разными длинами волн, которые кажутся нам окрашенными в разные цвета; цвета именно кажутся — это определенные ощущения. Свет от любого источника можно проанализировать с помощью дифракционной решетки или призмы и найти его спектральное распределение, т. е. «количество» света той или иной длины волны. Один луч света может содержать большое количество синего, немного красного и совсем мало желтого, другой содержит цвета в иной пропорции и т. д. Для физики такой характеристики будет вполне достаточно, но здесь нам надо ответить на вопрос: какого цвета будет луч, каким он нам покажется? Очевидно, что окраска как-то связана со спектральным распределением света, но наша задача состоит в том, чтобы найти, от какой именно характеристики спектрального распределения зависит восприятие того или иного цвета. Например, как получить зеленый цвет? Нам хорошо известно, что можно просто выбрать соответствующий участок спектра. А нет ли другого способа получить зеленый, оранжевый и вообще любой цвет?
Может ли быть несколько спектральных распределений, вызывающих один и тот же зрительный эффект? Ответ совершенно определенный — да, может. Число различных зрительных восприятий довольно ограниченно; как мы вскоре увидим, это число охватывает всего лишь трехмерное множество восприятий, а число кривых — спектральных распределений для разных источников — бесконечно. Возникает вопрос, который мы и обсудим в первую очередь: при каких условиях различные распределения выглядят как один и тот же цвет?
Самый действенный психофизический способ оценки цветовой чувствительности состоит в использовании глаза как нулевого прибора. При этом не нужно исследовать, как складывается ощущение зеленого цвета, или измерять факторы, которые вызывают ощущение зеленого цвета, это было бы слишком сложно. Вместо этого мы изучим условия, при которых два раздражения (два воздействия) становятся неразличимыми. При этом нам нет необходимости знать, могут ли два человека получить в разных условиях одинаковое зрительное ощущение, а нужно лишь установить, что два раздражения, вызывающие одинаковые ощущения у одного человека, приводят к одинаковым ощущениям и у другого. Совершенно излишне сравнивать зрительные ощущения двух разных людей, смотрящих на один и тот же, скажем, зеленый предмет. Об этом мы ничего не знаем.
Для иллюстрации возможностей этого метода возьмем набор из четырех проекционных фонарей, снабженных фильтрами. Их яркость может непрерывно меняться в широких пределах; первый фонарь имеет красный фильтр и отбрасывает на экран красное пятно, второй — зеленый фильтр и дает зеленое пятно, третий — синий фильтр, и, наконец, четвертый образует на экране белый круг с черным пятном посредине. Включим красный и зеленый фонари так, чтобы пятна света на экране частично перекрывались, тогда область перекрывшихся пятен вызовет у нас ощущение нового цвета, не красновато-зеленого, а желтого. Изменяя пропорцию красного и зеленого, можно пройти через всевозможные оттенки оранжевого и т. д. Установив на экране определенный желтый цвет, можно получить точно такой же цвет, смешивая другие компоненты, например используя желтый фильтр и смешав затем желтый свет с лучом белого цвета. Другими словами, одни и те же цвета можно создавать несколькими способами, смешивая свет от разных фильтров.
Открытое нами явление
аналитически можно записать следующим образом. Обозначим данный желтый цвет
символом ![]() ;
он представляет собой сумму некоторых количеств света от красного фильтра
;
он представляет собой сумму некоторых количеств света от красного фильтра ![]() и от зеленого
и от зеленого ![]() . С помощью двух
чисел, скажем
. С помощью двух
чисел, скажем ![]() и
и
![]() ,
определяющих яркости
,
определяющих яркости ![]() и
и ![]() , формула для желтого цвета
записывается в виде
, формула для желтого цвета
записывается в виде
![]() (35.1)
(35.1)
Вопрос теперь заключается в том, можно ли каждый цвет получить сложением двух или трех различных фиксированных цветов. Попробуем ответить на этот вопрос. Конечно, нельзя получить любой цвет, смешивая только зеленый и красный, потому что синий цвет в такой комбинации никогда не получится. Однако если добавить к ним синий, то в месте пересечения всех трех цветовых пятен можно добиться появления чистого белого цвета. Смешивая три разных цвета в разных пропорциях, в области пересечения можно получить цвета в очень широком диапазоне, поэтому не исключено, что смешение трех таких цветов может в принципе дать любой цвет. Мы потом рассмотрим, в какой мере это утверждение правильно; по существу оно верно, а вскоре мы сформулируем его более точно.
Совместим цветовые пятна от всех трех фонарей в одном месте и попытаемся подобрать такой же цвет, какой появляется во внешнем кольце от четвертого фонаря, опоясывающем пятно смешанного цвета. Свет от четвертого фонаря, который мы сначала считали «белым», теперь кажется бледно-желтым. Попытаемся подобрать этот цвет, смешивая красный, зеленый и синий; оказывается, методом проб и ошибок можно создать «кремовый» цвет, оттенок которого очень близок к нужному нам цвету. Поэтому легко поверить, что и любой цвет можно подобрать сочетанием красного, зеленого и синего цвета. Мы попробуем позже получить желтый цвет, но сначала хотелось бы создать один цвет, который получить очень трудно. Когда читают лекции о цвете, обычно демонстрируют «яркие» цвета и никогда не показывают коричневого; пожалуй, даже невозможно вспомнить, чтобы кто-либо видел коричневый свет. И действительно, этот свет никогда не используют, скажем, в сценических эффектах, и прожекторов с коричневым светом никто не видел; нее как будто указывает на то, что получить коричневый свет невозможно. По этому поводу стоит, однако, заметить, что мы просто не привыкли видеть коричневый свет сам по себе, без всякого фона. Практически его можно создать, смешивая в некоторой пропорции красный и желтый. Чтобы убедиться, что на экране действительно получился коричневый цвет, достаточно увеличить яркость окружающего фона, на котором расположено цветовое пятно, и вы увидите пятно того самого цвета, который мы называем коричневым! Коричневый цвет всегда выглядит темным на фоне более светлого окружения. Легко получить коричневый цвет самых разных оттенков. Например, если уменьшить долю желтого света, возникнет красновато-коричневый цвет с шоколадным оттенком, а если добавить зеленый, получится ужасный цвет военного обмундирования, принятый в армии. Но сам по себе свет, создающий этот цвет, не так уж страшен — он просто желтовато-зеленый цвет, который рассматривается на светлом фоне.
Поставим теперь желтый фильтр на четвертый фонарь и попробуем путем смешивания подобрать такой же желтый цвет. (Яркость четвертого фонаря должна находиться в пределах яркости первых трех, иначе мы не сумеем создать смешанный цвет точно такой же яркости.) Оказывается, мы можем получить желтый цвет; достаточно только смешать зеленый и красный, а для оттенка добавить немного синего. После этого уже нетрудно поверить, что при соответствующих условиях можно в точности подобрать любой заданный цвет.
Давайте обсудим теперь
законы смешивания цветов. Прежде всего, как мы уже говорили, один и тот же цвет
может быть создан различными спектральными распределениями; далее, мы заметили,
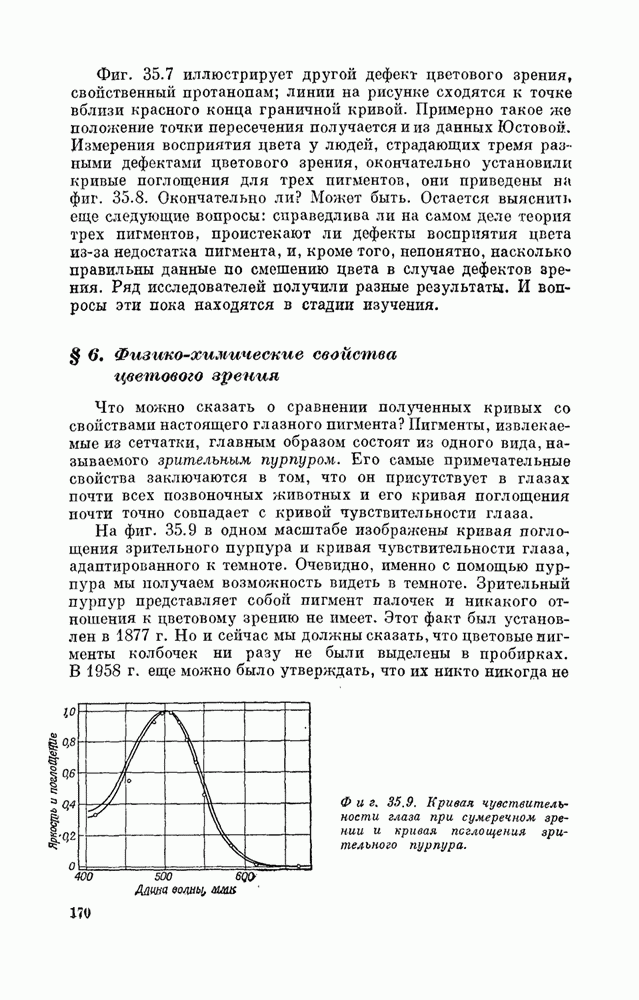
что «каждый» цвет может быть получен смешиванием трех основных цветов:
красного, синего и зеленого. Наиболее интересное свойство смеси цветов состоит
в следующем: пусть задан свет определенного состава, назовем его ![]() , который на глаз
неотличим от другого света
, который на глаз
неотличим от другого света ![]() (они могут иметь разные спектральные
распределения, но зрительно кажутся одинаковыми); назовем эти цвета
«одинаковыми» в том смысле, что глаз видит их как одинаковые, и запишем
(они могут иметь разные спектральные
распределения, но зрительно кажутся одинаковыми); назовем эти цвета
«одинаковыми» в том смысле, что глаз видит их как одинаковые, и запишем
![]() (35.2)
(35.2)
Прибавим к каждому цвету
новый, скажем ![]() (запись
(запись
![]() означает,
что два световых пучка падают на одно и то же место экрана), и точно такой же
пучок света добавим к
означает,
что два световых пучка падают на одно и то же место экрана), и точно такой же
пучок света добавим к ![]() . Тогда один из основных законов
цвета выражается так: если два спектральных распределения неразличимы на глаз
по цвету, то после добавления к ним одинакового количества нового цвета смеси
будут по-прежнему неразличимы:
. Тогда один из основных законов
цвета выражается так: если два спектральных распределения неразличимы на глаз
по цвету, то после добавления к ним одинакового количества нового цвета смеси
будут по-прежнему неразличимы:
![]() (35.3)
(35.3)
Мы только что смогли подобрать два одинаковых желтых цвета; если оба цвета осветить розовым светом, то они останутся одинаковыми. Итак, добавив любой цвет к одинаковым цветам, получим одинаковый цвет. Обобщая все цветовые явления этого рода, можно сказать и по-другому: если цвета двух расположенных рядом друг с другом лучей света в одних условиях выглядят одинаковыми, то при любых смешениях они останутся одинаковыми и один луч может быть заменен другим при любом смешении цветов. Важным и интересным оказывается также то обстоятельство, что совпадение цветов не зависит от свойств зрения в момент наблюдения; известно, что если долго смотреть на яркую красную поверхность или яркий красный свет, а затем взглянуть на белый лист бумаги, то он покажется зеленоватым и другие цвета также будут восприниматься с искажениями (из-за того, что мы долго перед этим смотрели на ярко-красный цвет). Пусть мы добились совпадения двух желтых цветов, а затем долго смотрели на яркий красный цвет; повернувшись снова к желтым пятнам, мы обнаружим, что они уже не кажутся нам больше желтыми (какими именно они будут казаться — я не знаю, но только не желтыми). Однако в любом случае оба цвета по-прежнему будут казаться одинаковыми, т. е. способность глаза приравнивать два цвета сохраняется, несмотря на адаптацию глаза в условиях разной интенсивности. Очевидным исключением является только случай очень малой интенсивности, когда функция зрения переходит от колбочек к палочкам; здесь уже нельзя говорить о сравнении цветов, так как система зрения совсем другая.
Второй закон смешения
цветов состоит в следующем: любой цвет может быть получен смешением трех разных
цветов (в нашем случае зеленого, красного и синего). Мы уже продемонстрировали
на двух примерах, что смешение трех цветов может дать самые разные цвета.
Описанные выше законы, кроме того, очень интересны с математической точки
зрения. Для тех, кого интересует математическая сторона проблемы, мы расскажем
о ней более подробно. Возьмем три наших цвета — зеленый, красный и синий,
обозначим их буквами ![]() и
и ![]() и назовем их основными. Тогда любой
цвет может быть получен смешением определенных количеств каждого из данных трех
цветов: например, цвет
и назовем их основными. Тогда любой
цвет может быть получен смешением определенных количеств каждого из данных трех
цветов: например, цвет ![]() создается смесью количества
создается смесью количества ![]() цвета
цвета ![]() , количества
, количества ![]() цвета
цвета ![]() и количества
и количества ![]() цвета
цвета ![]() :
:
![]() (35.4)
(35.4)
Составим теперь из тех же
трех цветов новый цвет ![]() :
:
![]() (35.5)
(35.5)
Тогда смесь цветов ![]() и
и ![]() определяется
суммами их компонент в основных цветах (как следствие двух главных законов
цвета, приведенных выше):
определяется
суммами их компонент в основных цветах (как следствие двух главных законов
цвета, приведенных выше):
![]() (35.6)
(35.6)
Это правило очень
напоминает суммирование векторов, причем ![]() играют роль компонент одного
вектора, а
играют роль компонент одного
вектора, а ![]() —
компонент второго, и новый свет
—
компонент второго, и новый свет ![]() определяется «суммой» векторов.
Такое соответствие постоянно привлекало к себе внимание физиков и математиков.
В частности, Шредингер написал замечательную работу о цветовом зрении, в
которой он развил теорию «векторного анализа» в применении к смеси цветов.
определяется «суммой» векторов.
Такое соответствие постоянно привлекало к себе внимание физиков и математиков.
В частности, Шредингер написал замечательную работу о цветовом зрении, в
которой он развил теорию «векторного анализа» в применении к смеси цветов.
Возникает вопрос: как нужно выбрать основные цвета? В самом деле, никакого единственно правильного выбора нет. С практической точки зрения иногда оказывается более полезным выбирать определенные три цвета, потому что они дают в смеси большее число оттенков, но мы не будем сейчас на этом останавливаться.
Любые три по-разному окрашенных пучка света могут образовать какой угодно другой цвет, если их смешать в нужной пропорции. Возможно ли показать на опыте действие этого удивительного, фантастического правила? Возьмем вместо красного, зеленого и синего света фонари с красным, синим, желтым фильтром и посмотрим, образует ли смесь этих цветов, скажем, зеленый цвет.
Смешивая эти три новых
цвета в разных пропорциях, мы получаем целый спектр разных цветов. Но после
целого ряда проб и ошибок мы убеждаемся, что ничего похожего на зеленый цвет
получить не удается. А можем ли мы вообще образовать зеленый цвет? Да, можем.
Но каким образом? Проектируя красный свет на зеленое пятно, мы можем затем
подобрать точно такой же цвет путем смешения желтого и синего! Таким путем мы
составляем две комбинации одного цвета, правда немного сжульничав, так как
поместили красный в другую комбинацию. Но поскольку мы уже умеем разбираться в
математических ухищрениях, то прекрасно понимаем, что вместо доказательства
возможности составления цвета ![]() из трех других цветов, например
желтого, красного и голубого, мы установили, что красный плюс цвет
из трех других цветов, например
желтого, красного и голубого, мы установили, что красный плюс цвет ![]() могут быть
сделаны из желтого и голубого. Перенесем теперь красный цвет в другую часть
равенства и будем интерпретировать его как отрицательную величину.
Следовательно, в уравнениях типа (35.4) возможны как положительные, так и
отрицательные значения коэффициентов, причем отрицательным величинам придается
такой смысл, что их следует перенести в другую часть равенства со знаком плюс,
тогда каждый цвет может быть действительно составлен из любых трех, и говорить
о каком-то «правильном» выборе основных цветов бессмысленно.
могут быть
сделаны из желтого и голубого. Перенесем теперь красный цвет в другую часть
равенства и будем интерпретировать его как отрицательную величину.
Следовательно, в уравнениях типа (35.4) возможны как положительные, так и
отрицательные значения коэффициентов, причем отрицательным величинам придается
такой смысл, что их следует перенести в другую часть равенства со знаком плюс,
тогда каждый цвет может быть действительно составлен из любых трех, и говорить
о каком-то «правильном» выборе основных цветов бессмысленно.
Возникает вопрос, всегда ли при составлении смеси любого цвета входят три основных цвета с положительными коэффициентами? Нет, не всегда. Для каждой тройки основных цветов имеются цвета, для которых в смеси появляется отрицательный коэффициент, и поэтому однозначного способа выбора основной тройки не существует. В популярных книжках красный, зеленый и синий обычно называют основными цветами, но это объясняется только тем, что с их помощью можно создать более широкий набор цветов при положительных значениях коэффициентов в комбинации основных.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
- § 4. Диаграмма цветности
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии