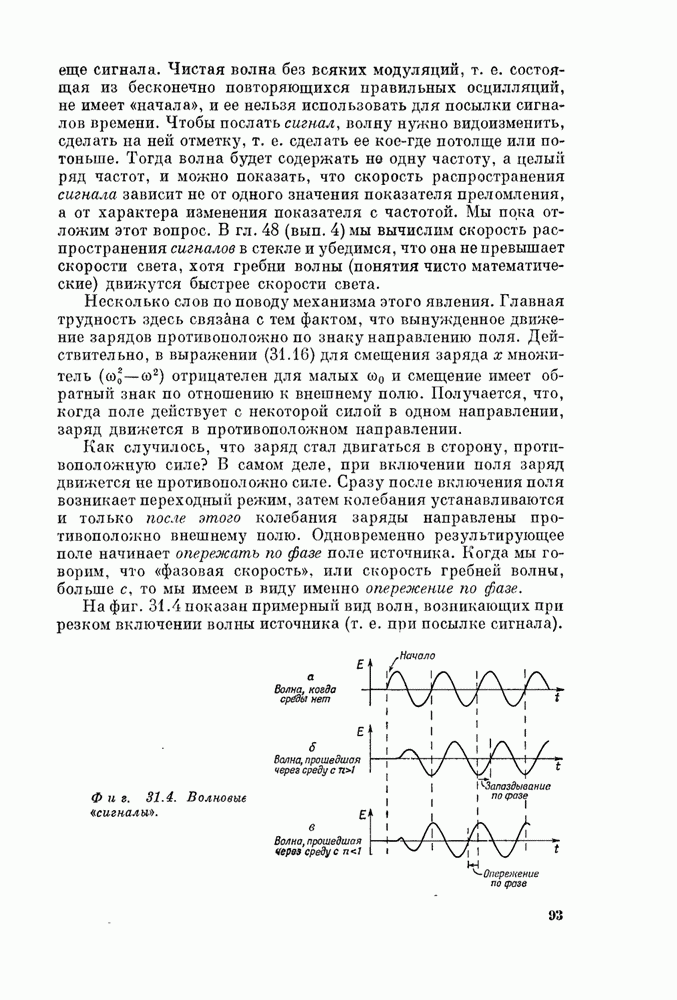
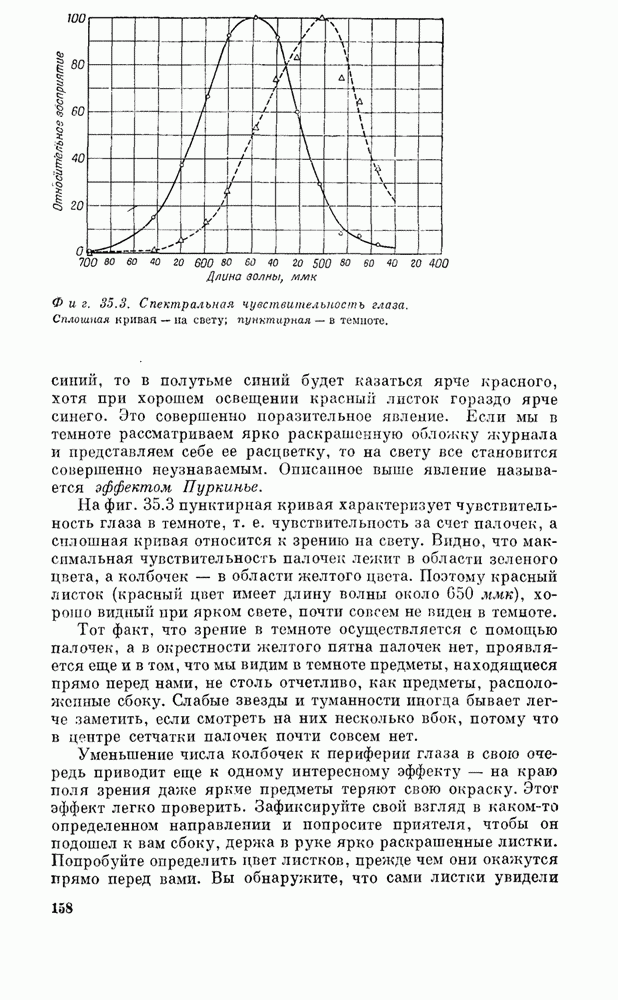
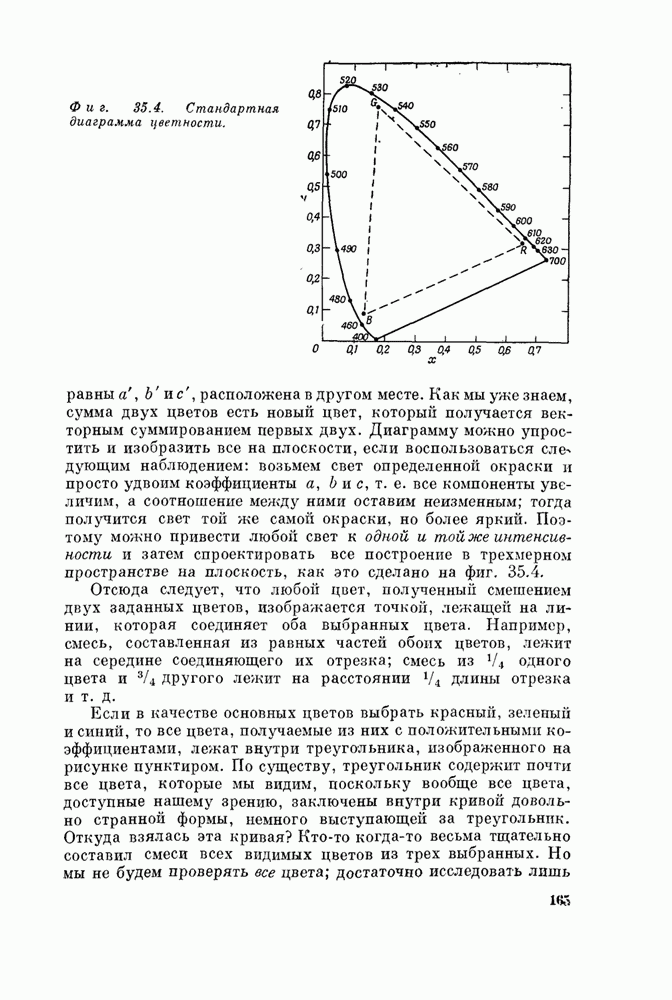
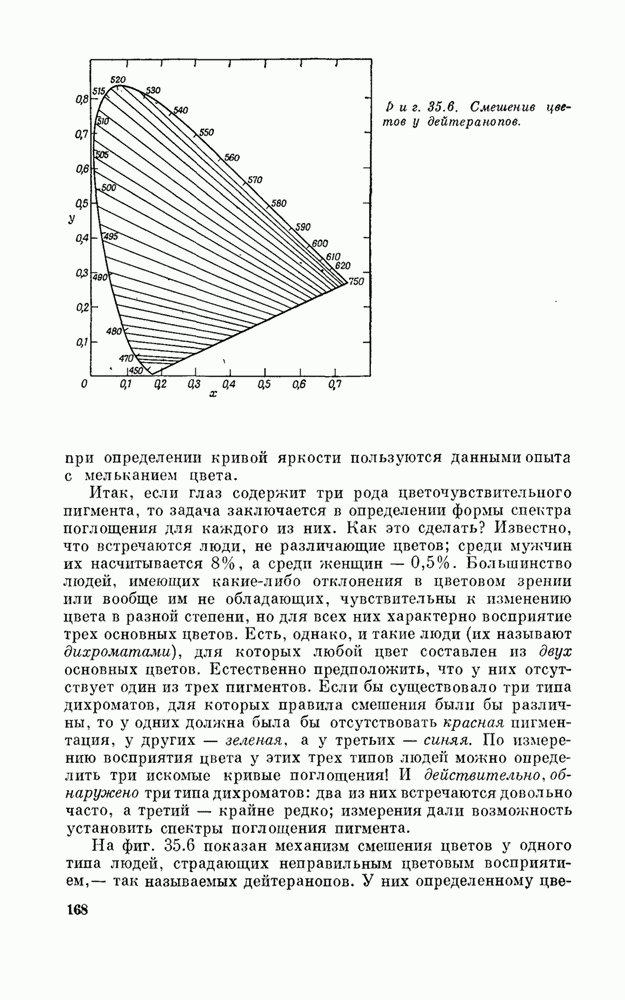
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Радиационное затухание
Заряд, закрепленный на
пружине с собственной частотой ![]() (или электрон в атоме), даже в
абсолютно пустом пространстве не сможет колебаться бесконечно долго, поскольку,
колеблясь, он теряет энергию на излучение. Никаких сил сопротивления в обычном
смысле этого слова, никакой вязкости здесь нет. Но колебания не будут
происходить «вечно», вследствие излучения они будут медленно замирать. А
насколько медленно? Определим для осциллятора величину
(или электрон в атоме), даже в
абсолютно пустом пространстве не сможет колебаться бесконечно долго, поскольку,
колеблясь, он теряет энергию на излучение. Никаких сил сопротивления в обычном
смысле этого слова, никакой вязкости здесь нет. Но колебания не будут
происходить «вечно», вследствие излучения они будут медленно замирать. А
насколько медленно? Определим для осциллятора величину ![]() , вызванную так называемым
радиационным сопротивлением или радиационным затуханием. Для любой колеблющейся
системы величина
, вызванную так называемым
радиационным сопротивлением или радиационным затуханием. Для любой колеблющейся
системы величина ![]() равна энергии системы в данный
момент времени, деленной на потери энергии, отнесенные к
равна энергии системы в данный
момент времени, деленной на потери энергии, отнесенные к ![]() :
:
![]()
Запишем ![]() по-другому, пользуясь для этого
равенством
по-другому, пользуясь для этого
равенством ![]() :
:
![]() (32.8)
(32.8)
Если ![]() задано, то легко получить
закон спадания энергии колебаний:
задано, то легко получить
закон спадания энергии колебаний: ![]() , откуда следует
, откуда следует ![]() ; здесь
; здесь ![]() — начальная энергия (при
— начальная энергия (при ![]() ).
).
Чтобы найти ![]() для излучающего
осциллятора, вернемся к формуле (32.8) и подставим вместо
для излучающего
осциллятора, вернемся к формуле (32.8) и подставим вместо ![]() выражение (32.6).
выражение (32.6).
А что нужно взять в
качестве энергии ![]() осциллятора? Кинетическая энергия
осциллятора равна
осциллятора? Кинетическая энергия
осциллятора равна ![]() , а средняя кинетическая энергия
равна
, а средняя кинетическая энергия
равна ![]() .
Но мы помним, что полная энергия осциллятора равна средней кинетической плюс
средняя потенциальная, причем обе они для осциллятора равны; поэтому полная
энергия равна
.
Но мы помним, что полная энергия осциллятора равна средней кинетической плюс
средняя потенциальная, причем обе они для осциллятора равны; поэтому полная
энергия равна
![]() (32.9)
(32.9)
Какую частоту следует
подставить в наши формулы? Мы возьмем собственную частоту ![]() , потому что практически
это и есть частота излучения атома, а вместо
, потому что практически
это и есть частота излучения атома, а вместо ![]() подставим
подставим ![]() . После ряда сокращений эта
формула приводится к виду
. После ряда сокращений эта
формула приводится к виду
 (32.10)
(32.10)
(Для большей ясности и из
соображений близости к исторически принятой форме мы ввели величину ![]() и записали
и записали ![]() вместо
вместо ![]() .) Поскольку
величина
.) Поскольку
величина ![]() безразмерна,
множитель
безразмерна,
множитель ![]() ,
зависящий только от массы и заряда электрона и выражающий его внутренние
свойства, обязан иметь размерность длины. Он был назван классическим радиусом
электрона, потому что в старых моделях электрона радиационное сопротивление
пытались объяснить действием одной части электрона на другие его части, для
чего размеры электрона приходилось выбирать порядка
,
зависящий только от массы и заряда электрона и выражающий его внутренние
свойства, обязан иметь размерность длины. Он был назван классическим радиусом
электрона, потому что в старых моделях электрона радиационное сопротивление
пытались объяснить действием одной части электрона на другие его части, для
чего размеры электрона приходилось выбирать порядка ![]() . Но эта величина потеряла
свой прежний смысл, и никто теперь не считает, что электрон имеет такой радиус.
Численное значение классического радиуса электрона следующее: 2
. Но эта величина потеряла
свой прежний смысл, и никто теперь не считает, что электрон имеет такой радиус.
Численное значение классического радиуса электрона следующее: 2
 (32.11)
(32.11)
Вычислим теперь значение ![]() для атома,
излучающего видимый свет, например для атома натрия. Длина волны излучения
натрия равна примерно
для атома,
излучающего видимый свет, например для атома натрия. Длина волны излучения
натрия равна примерно ![]() и находится в желтой части спектра;
эта величина довольно типична. Отсюда
и находится в желтой части спектра;
эта величина довольно типична. Отсюда
![]() , (32.12)
, (32.12)
т. е. для атомов ![]() порядка
порядка ![]() . Это значит, что
атомный осциллятор колеблется
. Это значит, что
атомный осциллятор колеблется ![]() , или примерно
, или примерно ![]() периодов, прежде чем его
энергия уменьшится в
периодов, прежде чем его
энергия уменьшится в ![]() . Частота колебании света
. Частота колебании света ![]() при длине волны
при длине волны ![]() составляет
составляет ![]() , а,
следовательно, время жизни, т. е. время, за которое энергия уменьшится в
, а,
следовательно, время жизни, т. е. время, за которое энергия уменьшится в ![]() , есть величина
порядка
, есть величина
порядка ![]() .
.
Примерно за такое же время высвечиваются свободные атомы в обычных условиях. Проведенная оценка справедлива только для атомов в пустом пространстве, не подверженных никаким внешним воздействиям. Если электрон находится в твердом теле, он сталкивается с другими атомами и электронами, и тогда возникает добавочное сопротивление и затухание будет другим.
Величина эффективного
сопротивления ![]() ,
определяющая сопротивление осциллятора, может быть найдена из соотношения
,
определяющая сопротивление осциллятора, может быть найдена из соотношения ![]() ; вспомним, что
именно
; вспомним, что
именно ![]() определяет
ширину резонансной кривой (см. фиг. 23.2). Итак, мы вычислили ширины
спектральных линий для свободно излучающих атомов! Из равенства
определяет
ширину резонансной кривой (см. фиг. 23.2). Итак, мы вычислили ширины
спектральных линий для свободно излучающих атомов! Из равенства ![]() получаем
получаем
![]() (32.13)
(32.13)
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
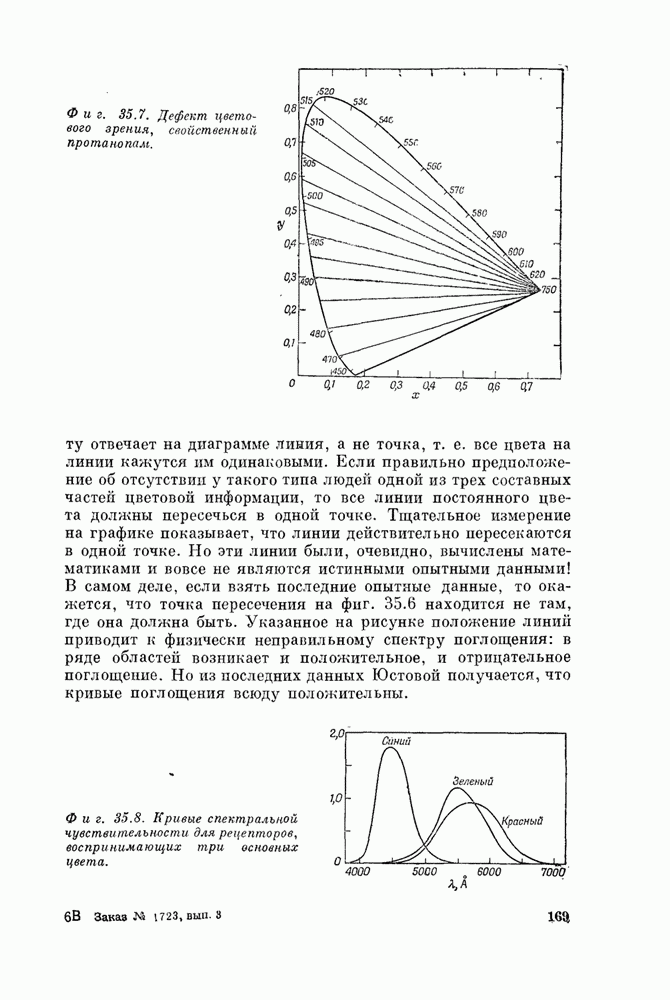
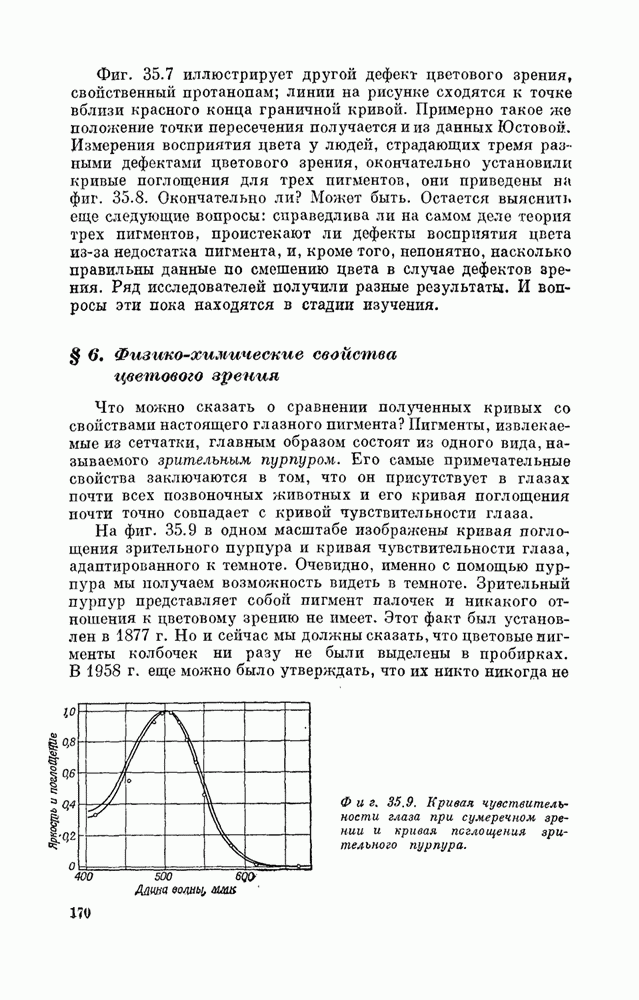
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
- § 4. Диаграмма цветности
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии