| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 38. Соотношение между волновой и корпускулярной точками зрения
§ 1. Волны амплитуды вероятности
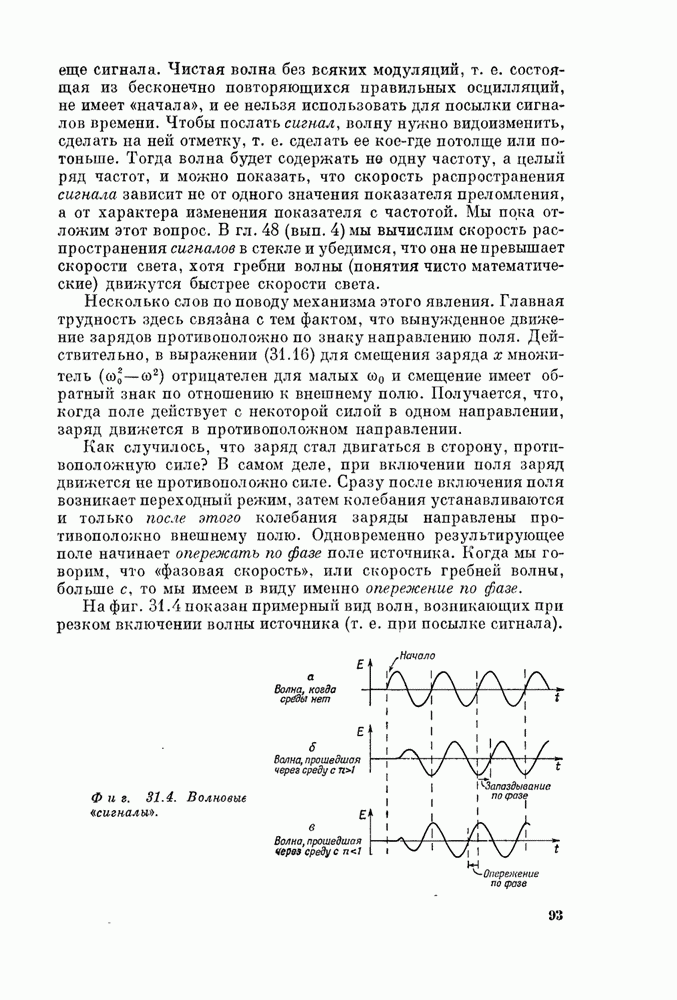
В этой главе мы с вами обсудим соотношение между волновой и корпускулярной точками зрения. Из предыдущей главы мы уже знаем, что ни та, ни другая неверны. Обычно мы всегда старались формулировать понятия аккуратно или по крайней мере достаточно точно, чтобы при дальнейшем изучении их не пришлось бы менять. Разрешалось их расширять, обобщать, но уже никак не менять! Но как только мы пытаемся говорить об электроне как волне или об электроне как частице, то любая из этих точек зрения рано или поздно меняется, ведь обе они приблизительны. Поэтому все, что мы изучим в этой главе, в каком-то смысле неправильно; будут высказаны некие полуинтуитивные соображения, которым со временем предстоит уточняться, и кое-что придется слегка изменить, когда мы их уточним с помощью квантовой механики. Причина в том, что, не собираясь сейчас штудировать квантовую механику по всем правилам, мы хотим получить по крайней мере представление о характере эффектов, которые мы там обнаружим. Да и к тому же весь наш опыт относится либо к волнам, либо к частицам, и поэтому весьма удобно использовать то те, то другие представления, чтобы добиться некоторого понимания того, что произойдет в определенных обстоятельствах, пока мы еще не знаем всей математики квантовомеханических амплитуд. По мере нашего продвижения вперед мы будем стараться прояснять самые слабые места. Впрочем, многие из этих мест почти верны, все дело просто в толковании.
Прежде всего мы уже знаем, что новый, выдвигаемый квантовой механикой способ изображать мир — новая система мира — состоит в том, чтобы задавать амплитуду любого события, которое может случиться. Если событие состоит в регистрации частицы, то можно задать амплитуду обнаружения этой частицы в тех или иных местах и в то или иное время. Вероятность обнаружить частицу тогда будет пропорциональна квадрату абсолютной величины амплитуды. Вообще говоря, вероятность обнаружить частицу в каком-то месте и в какое-то время меняется в зависимости от места и от времени.
В частном случае амплитуда может изменяться синусоидально в пространстве
и времени по закону ![]() у (не забывайте, что амплитуда —
число комплексное, а не действительное); тогда в нее входит определенная
частота
у (не забывайте, что амплитуда —
число комплексное, а не действительное); тогда в нее входит определенная
частота ![]() и
определенный волновой вектор
и
определенный волновой вектор ![]() (величина
(величина ![]() называется волновым
числом). Это отвечает той предельной классической ситуации, когда можно
считать, что имеется частица с известной энергией
называется волновым
числом). Это отвечает той предельной классической ситуации, когда можно
считать, что имеется частица с известной энергией ![]() , которая связана с частотой
соотношением
, которая связана с частотой
соотношением
![]() (38.1)
(38.1)
и с известным импульсом ![]() , связанным с волновым вектором
формулой
, связанным с волновым вектором
формулой
![]() (38.2)
(38.2)
Это означает, что понятие частицы ограниченно. Само понятие частицы,
понятие ее положения, ее импульса и т. д., которым мы так часто пользуемся, в
некотором смысле не является удовлетворительным. Например, когда амплитуда,
относящаяся к событию обнаружения частицы в том или ином месте, дается функцией
![]() ,
равной по абсолютной величине единице, то это значит, что вероятность
обнаружить частицу одинакова для любой точки. Получается, что тогда мы просто
не знаем, где она находится. Она может оказаться где угодно, ее положение в
высшей степени неопределенно.
,
равной по абсолютной величине единице, то это значит, что вероятность
обнаружить частицу одинакова для любой точки. Получается, что тогда мы просто
не знаем, где она находится. Она может оказаться где угодно, ее положение в
высшей степени неопределенно.
Когда же положение частицы более или менее известно, когда оно может быть
предсказано довольно точно, то вероятность того или иного ее местоположения
должна быть отлична от нуля в определенной области, имеющей, скажем, длину ![]() . Вне этой области
вероятность равна нулю. Вероятность — это квадрат абсолютной величины
амплитуды. Когда квадрат абсолютной величины равен нулю, то и амплитуда равна нулю.
. Вне этой области
вероятность равна нулю. Вероятность — это квадрат абсолютной величины
амплитуды. Когда квадрат абсолютной величины равен нулю, то и амплитуда равна нулю.
Выходит, что амплитуда описывает цуг волн протяженностью ![]() (фиг. 38.1), а
длине волны (расстоянию между горбами волн) в цуге волн соответствует некоторое
значение импульса частицы.
(фиг. 38.1), а
длине волны (расстоянию между горбами волн) в цуге волн соответствует некоторое
значение импульса частицы.

Фигура 38.1. Волновой пакет длиной ![]() .
.
Здесь мы сталкиваемся со странным и в то же время очень простым явлением, никак непосредственно с квантовой механикой не связанным. Оно известно всем, кто занимался волнами, даже не зная квантовой механики, а именно: нельзя однозначно определить длину волны для короткого цуга волн. У такого цуга нет определенной длины волн; в волновом числе имеется неопределенность, связанная с конечной длиной цуга, а значит, и неопределенность в импульсе.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
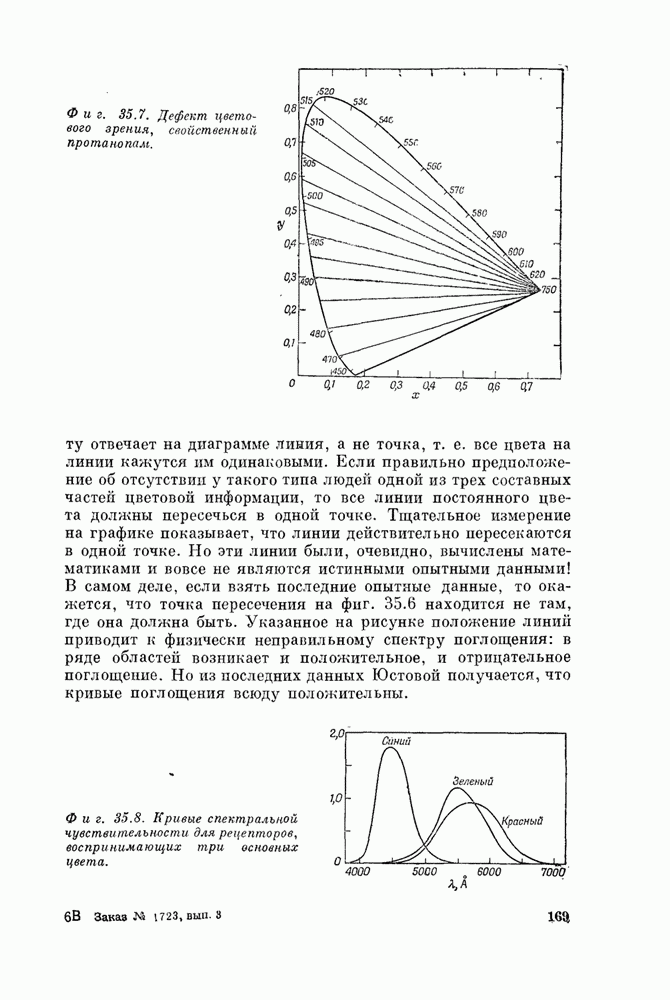
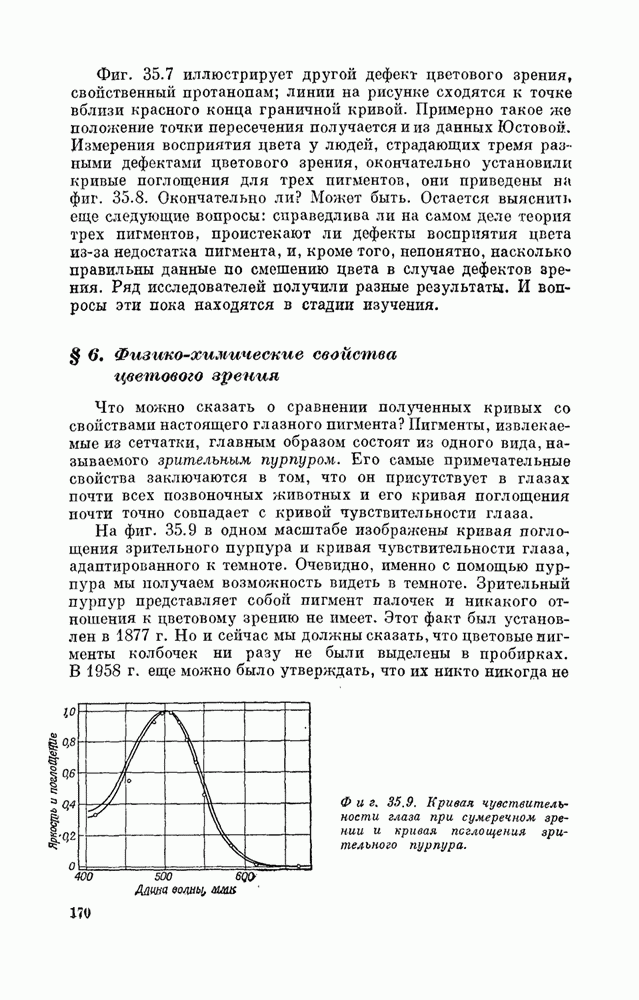
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
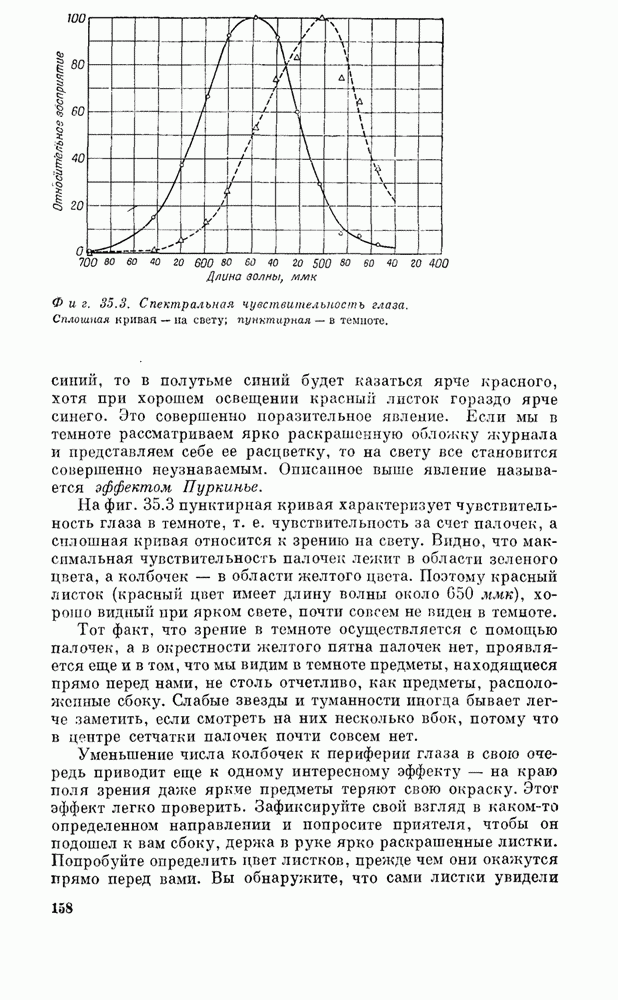
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
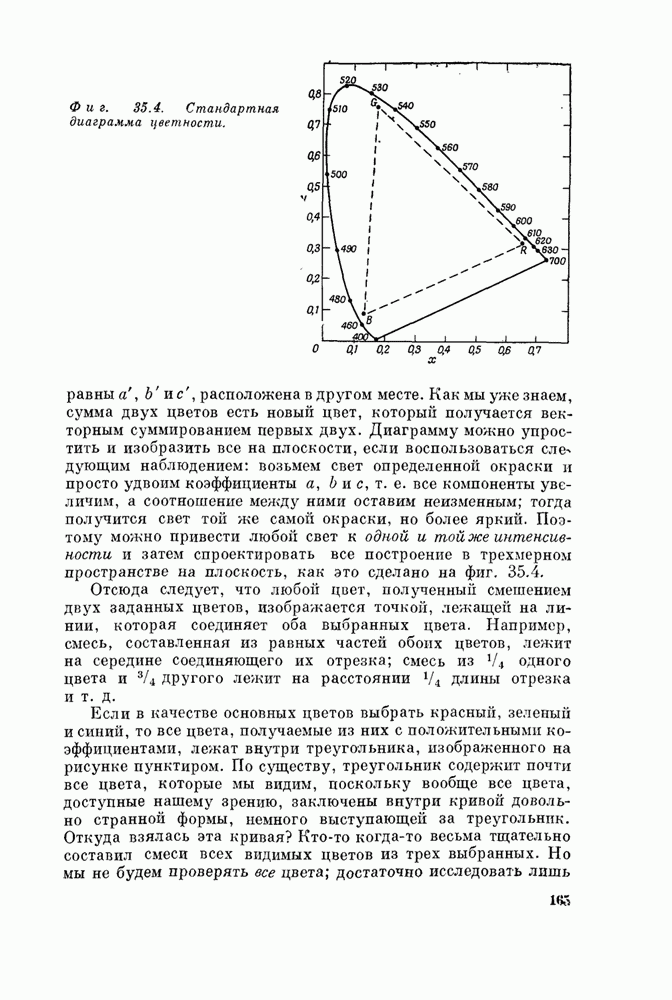
- § 4. Диаграмма цветности
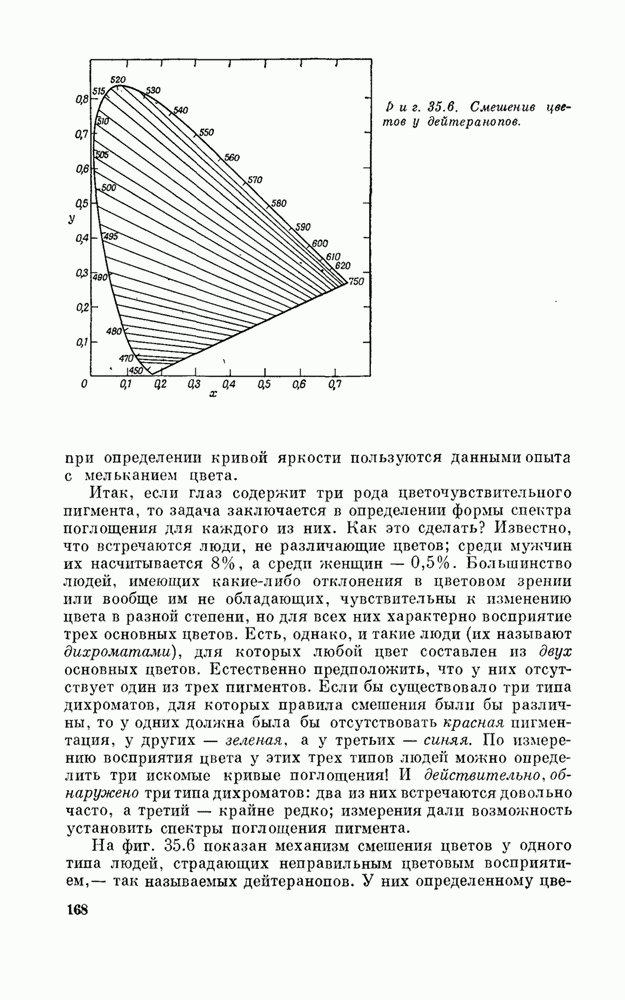
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии