§ 6. Дифракция на непрозрачном экране

Рассмотрим сейчас весьма интересное явление. Пусть имеется непрозрачный лист с отверстиями, и по одну сторону от него расположен источник света. Нас интересует, какое изображение возникнет на экране по другую сторону листа. Каждый скажет, что свет пройдет через отверстия и создаст на экране какое-то изображение. Оказывается, что это изображение можно получить с хорошей степенью точности, если предположить, что источники света равномерно распределены по ширине отверстий, а фазы источников точно такие, как если бы непрозрачного листа вовсе не было. Источников в отверстиях на самом деле, конечно, нет; во всяком случае, это как раз то место, где их наверняка не может быть. Тем не менее правильная дифракционная картина получается, если считать, что источники расположены именно в отверстиях; факт довольно странный. Позже мы объясним, почему такое предположение правильно, а пока примем его на веру.

В теории дифракции есть один род дифракционных явлений, который стоит кратко обсудить. Речь идет о дифракции на непрозрачных экранах. Обычно в элементарных курсах о них говорят гораздо позже, так как для их объяснения нужно использовать довольно сложные формулы суммирования малых векторов. В остальном эти явления не отличаются от уже рассмотренных нами. Все интерференционные явления по существу одинаковы; в них не входят сколько-нибудь сложные понятия, только условия возникновения могут быть более сложными, и тогда векторы поля труднее складывать, вот и все.

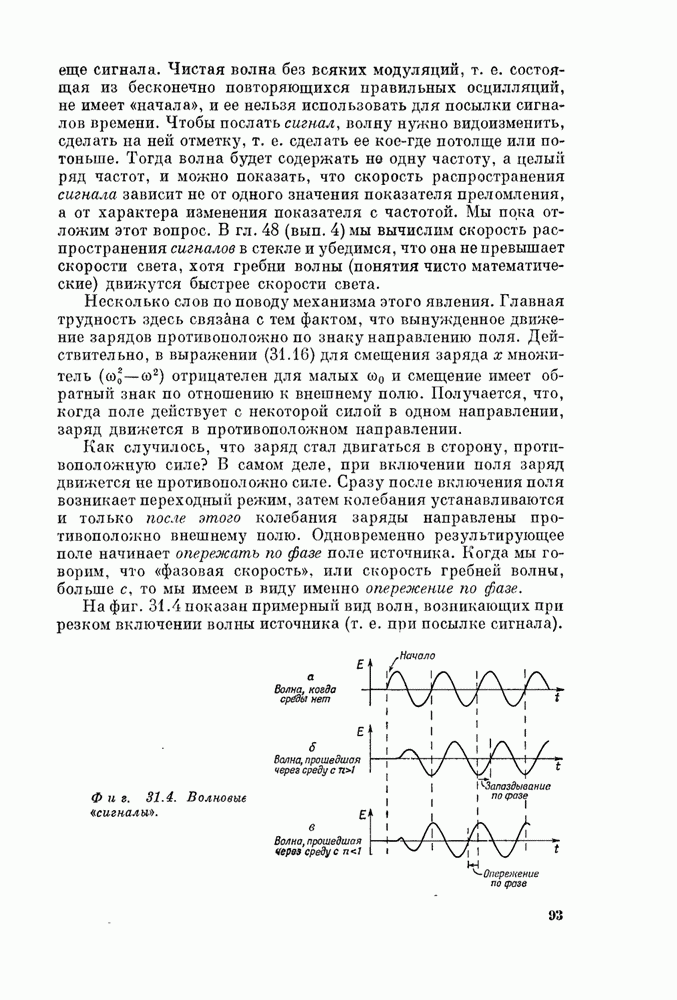
Предположим, что свет приходит из бесконечности, попадает на предмет и отбрасывает от него тень. На фиг. 30.7 изображен экран, на который свет отбрасывает тень от предмета , причем источник света удален на расстояние, много большее длины волны. Казалось бы, вне тени интенсивность света максимальна, а внутри должна быть полная темнота. На самом же деле, если откладывать интенсивность как функцию расстояния до края тени, интенсивность будет сначала расти, а затем начнет спадать, колеблясь самым прихотливым образом вблизи края тени (фиг. 30.8). Посмотрим, отчего это происходит. Для объяснения воспользуемся недоказанной нами теоремой, что вместо истинной картины опыта можно ввести эффективные источники, равномерно распределенные вне объекта.

Фигура 30.7. Далекий источник отбрасывает тень от непрозрачного предмета на экран.

Представим себе эти эффективные источники в виде большого количества близко расположенных антенн и найдем интенсивность в некоторой точке . Это очень похоже на то, чем мы занимались до сих пор. Но не вполне, поскольку наш экран теперь находится не на бесконечности. В данном случае нас интересует интенсивность интерферирующих лучей на конечном расстоянии, а не на бесконечности. Интенсивность в некоторой точке дается суммой вкладов от каждой антенны. Сначала возьмем антенну в точке , прямо напротив . Если слегка изменить угол, скажем, подняться на высоту , лучу потребуется больше временя, чтобы попасть в точку  (амплитуда тоже изменится, так как расстояние до источника увеличилось, но разница эта очень мала, поскольку расстояние все равно велико, и гораздо менее важна, чем изменение фазы излучения). Далее, разность  равна , т. е. разность фаз пропорциональна квадрату удаления от точки , тогда как раньше у нас  было бесконечно и разность фаз была линейно связана с . Когда фазы зависят от  линейно, каждый вектор повернут относительно предыдущего на постоянный угол. Теперь же мы должны построить кривую, складывая бесконечно малые векторы при условии, что образуемый ими угол с осью абсцисс растет с увеличением длины кривой не линейным, а квадратичным образом. Явный вид кривой находится с помощью довольно сложных математических методов, но мы всегда можем построить эту кривую, просто откладывая векторы под требуемым углом. В конечном счете мы получаем замечательную кривую (называемую спиралью Корню), изображенную на фиг. 30.8. Как ею пользоваться? . Пусть требуется определить интенсивность, скажем, в точке.

Фигура 30.8. Сложение амплитуд большого числа осцилляторов, излучающих с одной фазой. Разность фаз за счет запаздывания пропорционадьна квадрату расстояния до точки  на фиг. 30.7.

Сложим волны с разными фазами от точки  вверх до бесконечности и вниз от  до точки . Таким образом, нужно отложить ряд стрелок под постоянно растущим углом, начиная с точки  на фиг. 30.8. Весь вклад от области над  дается спиральной кривой. Если бы суммирование заканчивалось в некоторой точке, то полная амплитуда представилась бы вектором от  до этой точки; в нашем случае суммирование ведется до бесконечности, так что искомая амплитуда есть вектор . Точка на кривой, соответствующая точке  на предмете, зависит от положения точки , потому что точка  кривой (точка перегиба) всегда относится к выбранной точке . Следовательно, в зависимости от положения  над  начальная точка, откуда проводится вектор, попадает в разные места нижней спирали, и результирующий вектор  имеет многочисленные максимумы и минимумы (фиг. 30.9).

Фигура 30.9. Ход интенсивности вблизи края тени. Геометрический край тени находится в точке .

Но если мы находимся в точке , по другую сторону от , то нам понадобится только верхний конец спиральной кривой. Другими словами, начальной точкой результирующего вектора будет не , а , и, следовательно, книзу от  интенсивность должна непрерывно падать при удалении  в область тени.

Есть одна величина, которую можно легко вычислить сразу и таким образом убедиться, что мы здесь что-то понимаем, — это интенсивность в точке, лежащей прямо против края. Эта интенсивность равна  от интенсивности падающего света. Причина: для точки, лежащей против края предмета (когда  совпадает с  на фиг. 30.8), получается половина кривой в отличие от целой кривой, которая была бы получена, если бы точки лежали достаточно далеко в освещенной области. Если точка  расположена достаточно высоко, результирующий вектор проводится от центра одной спирали до центра другой, а для точки на краю тени амплитуда равна половине этого вектора; следовательно, отношение интенсивностей получается равным .

В этой главе мы вычисляли интенсивность в разных направлениях при различном расположении источников. В заключение выведем формулу, которая нам понадобится в следующей главе, посвященной показателю преломления. До сих пор мы обходились только относительными интенсивностями, а на этот раз мы получим формулу для полной величины поля при условиях, о которых будет рассказано ниже.