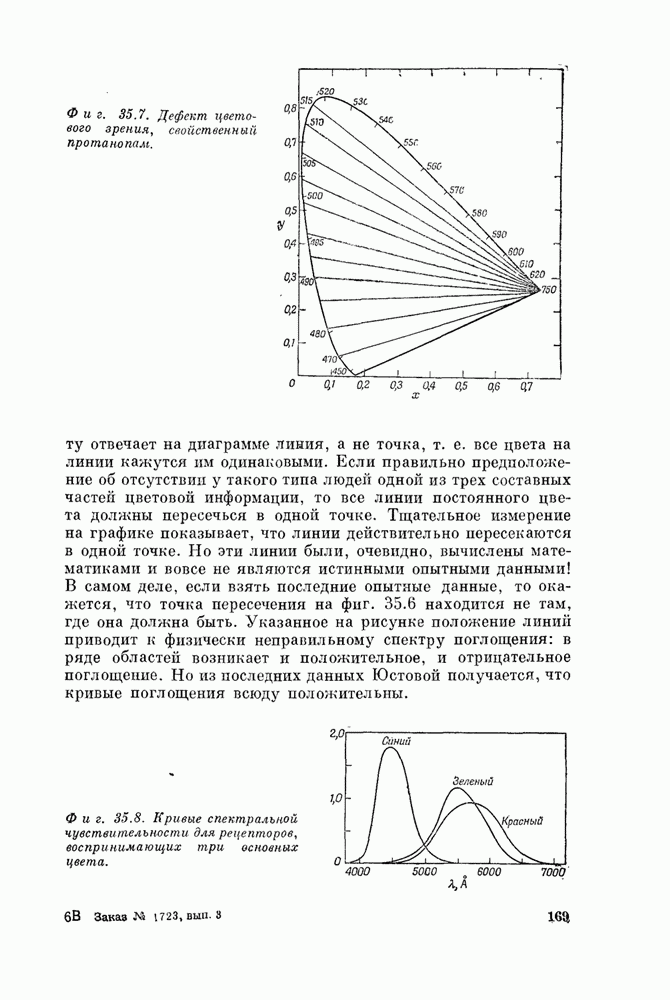
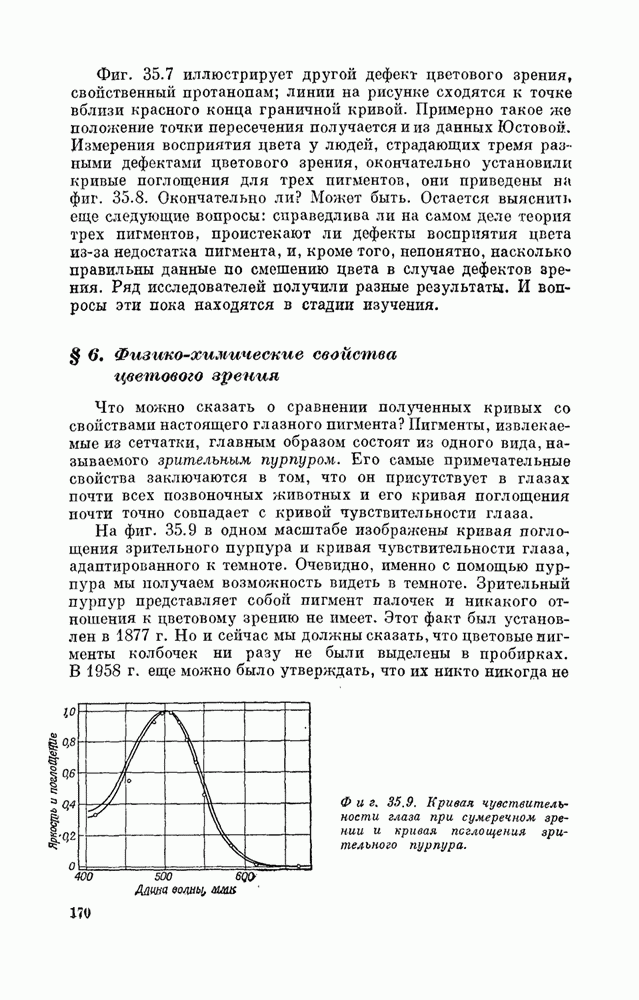
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Принцип наименьшего времени Ферма
По мере развития науки нам хочется получить нечто большее, чем просто формулу. Сначала мы наблюдаем явления, затем с помощью измерений получаем числа и, наконец, находим закон, связывающий эти числа. Но истинное величие науки состоит в том, что мы можем найти такой способ рассуждения, при котором закон становится очевидным.
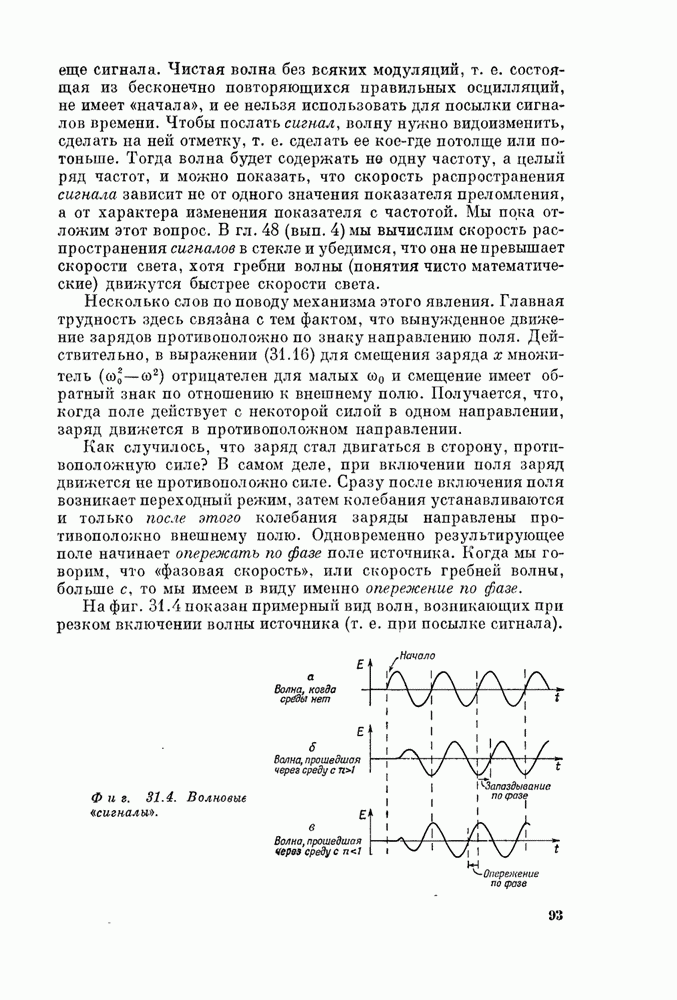
Впервые общий принцип, наглядно объясняющий закон поведения света, был предложен Ферма примерно в 1950 г. и получил название принципа наименьшего времени, или принципа Ферма. Вот его идея: свет выбирает ив всех возможных путей, соединяющих две точки, тот путь, который требует наименьшего времени для его прохождения.
Покажем сначала, что это верно для случая с зеркалом, что этот простой принцип объясняет и прямолинейность распространения света, и закон отражения света от зеркала. Мы явно делаем успехи!
Попытаемся решить
следующую задачу. На фиг. 26.3 изображены две точки ![]() и
и ![]() и плоское зеркало
и плоское зеркало ![]() . Каким путем можно
за кратчайшее время попасть из точки
. Каким путем можно
за кратчайшее время попасть из точки ![]() в точку
в точку ![]() ? Ответ: по прямой, проведенной из
? Ответ: по прямой, проведенной из ![]() в
в ![]() !
!

Фигура 26.3. Иллюстрация принципа наименьшего времени.
Но если мы добавим
дополнительное условие, что свет должен попасть на зеркало, отразиться от негой
вернуться снова в точку В опять-таки за кратчайшее время, то ответить не так уж
просто. Один путь — как можно скорее добраться до зеркала, а оттуда в точку ![]() , т. е. по пути
, т. е. по пути ![]() . Путь
. Путь ![]() , конечно, длинен.
Если сдвинуться чуть-чуть вправо в точку
, конечно, длинен.
Если сдвинуться чуть-чуть вправо в точку ![]() , то первый отрезок пути немного
увеличится, но зато сильно уменьшится второй, и время прохождения поэтому станет
меньше. Как найти точку
, то первый отрезок пути немного
увеличится, но зато сильно уменьшится второй, и время прохождения поэтому станет
меньше. Как найти точку ![]() , для которой время прохождения
наименьшее? Воспользуемся для этого хитрым геометрическим приемом.
, для которой время прохождения
наименьшее? Воспользуемся для этого хитрым геометрическим приемом.
По другую сторону зеркала
![]() , на
таком же расстоянии от него, что и точка
, на
таком же расстоянии от него, что и точка ![]() , построим искусственную точку
, построим искусственную точку ![]() . Затем проведем
линию
. Затем проведем
линию ![]() .
Поскольку угол
.
Поскольку угол ![]() прямой
и
прямой
и ![]() , то
, то ![]() равно
равно ![]() . Следовательно,
сумма длин двух отрезков
. Следовательно,
сумма длин двух отрезков ![]() , пропорциональная времени их
прохождения (если свет проходит с постоянной скоростью), равна сумме длин
, пропорциональная времени их
прохождения (если свет проходит с постоянной скоростью), равна сумме длин ![]() . Теперь нужно
выяснить, когда сумма длин будет наименьшей. Ответ: когда точка
. Теперь нужно
выяснить, когда сумма длин будет наименьшей. Ответ: когда точка ![]() будет лежать на
прямой, соединяющей
будет лежать на
прямой, соединяющей ![]() и
и ![]() ! Другими словами, нужно идти к мнимой
точке
! Другими словами, нужно идти к мнимой
точке ![]() (мнимому
изображению точки
(мнимому
изображению точки ![]() ) и тогда мы найдем точку
) и тогда мы найдем точку ![]() . Далее, если
. Далее, если ![]() — прямая линия, угол
— прямая линия, угол
![]() равен
углу
равен
углу ![]() и,
следовательно, углу
и,
следовательно, углу ![]() . Таким образом, утверждение о
равенстве углов падения и отражения равносильно утверждению, что свет при
отражении от зеркала в точку
. Таким образом, утверждение о
равенстве углов падения и отражения равносильно утверждению, что свет при
отражении от зеркала в точку ![]() выбирает путь, требующий наименьшего
времени. Еще Герон Александрийский высказал утверждение, что свет при отражении
идет из одной точки в другую по кратчайшему пути, так что идея принципа, как
видите, не нова. Именно это вдохновило Ферма, и он попробовал применить этот
принцип к явлению преломления. Но свет, преломляясь, очевидным образом идет не
по кратчайшему пути, и тогда Ферма предложил другой принцип — свет выбирает
путь, время прохождения по которому наименьшее.
выбирает путь, требующий наименьшего
времени. Еще Герон Александрийский высказал утверждение, что свет при отражении
идет из одной точки в другую по кратчайшему пути, так что идея принципа, как
видите, не нова. Именно это вдохновило Ферма, и он попробовал применить этот
принцип к явлению преломления. Но свет, преломляясь, очевидным образом идет не
по кратчайшему пути, и тогда Ферма предложил другой принцип — свет выбирает
путь, время прохождения по которому наименьшее.
Прежде чем перейти к вопросу
о преломлении света, сделаем еще одно замечание об отражении от зеркала. Если
поместить источник света в точку ![]() и направить луч на зеркало, свет, отражаясь
от зеркала, пройдет из
и направить луч на зеркало, свет, отражаясь
от зеркала, пройдет из ![]() в
в ![]() так, как будто бы источник находится
в
так, как будто бы источник находится
в ![]() , а
зеркала нет вообще. Haш глаз видит только тот свет, который действительно
входит в него; и хотя источник расположен в точке
, а
зеркала нет вообще. Haш глаз видит только тот свет, который действительно
входит в него; и хотя источник расположен в точке ![]() , зеркало направляет свет в глаз точно
так, как будто источник находится в
, зеркало направляет свет в глаз точно
так, как будто источник находится в ![]() , и система глаза — мозг интерпретирует
именно так это явление. Поэтому иллюзия, что источник или предмет находится за
зеркалом, вызывается только тем фактом, что свет попадает в глаз физически
именно так, как если бы предмет действительно был позади зеркала (если не
принимать во внимание пыль на зеркале и то, что нам известно, что зеркало
реально существует, и другие сведения, которые учитывает наш мозг).
, и система глаза — мозг интерпретирует
именно так это явление. Поэтому иллюзия, что источник или предмет находится за
зеркалом, вызывается только тем фактом, что свет попадает в глаз физически
именно так, как если бы предмет действительно был позади зеркала (если не
принимать во внимание пыль на зеркале и то, что нам известно, что зеркало
реально существует, и другие сведения, которые учитывает наш мозг).
Покажем теперь, что из
принципа наименьшего времени вытекает закон Снелла для преломления. Мы должны,
конечно, что-то предположить относительно скорости света в воде. Будем считать,
что скорость света в воде меньше скорости света в воздухе, и отношение второй
скорости к первой обозначим через ![]() .
.
Наша задача по-прежнему
состоит в том, чтобы на фиг. 26.4 попасть из точки ![]() в
в ![]() за наименьшее время. Чтобы
убедиться, что путь по прямой здесь не самый быстрый, представим себе следующую
ситуацию: хорошенькая девушка падает из лодки в воду в точке
за наименьшее время. Чтобы
убедиться, что путь по прямой здесь не самый быстрый, представим себе следующую
ситуацию: хорошенькая девушка падает из лодки в воду в точке ![]() и кричит, просит
спасти. Линия
и кричит, просит
спасти. Линия ![]() —
это берег. Вы находитесь на суше в точке
—
это берег. Вы находитесь на суше в точке ![]() и видите, что произошло, вы умеете
плавать и умеете бегать. Но бегаете вы быстрее, чем плаваете. Что вам делать?
Бежать по прямой к берегу? (Конечно!) Но, немного поразмыслив, вы поймете, что
выгоднее пробежать несколько дольше по берегу, чтобы уменьшить ваш путь в воде,
потому что в воде вы будете двигаться гораздо медленнее. (Рассуждая таким
образом, лучше всего было бы заранее тщательно вычислить путь!) Во всяком случае,
давайте попытаемся показать, что окончательное решение задачи — это путь
и видите, что произошло, вы умеете
плавать и умеете бегать. Но бегаете вы быстрее, чем плаваете. Что вам делать?
Бежать по прямой к берегу? (Конечно!) Но, немного поразмыслив, вы поймете, что
выгоднее пробежать несколько дольше по берегу, чтобы уменьшить ваш путь в воде,
потому что в воде вы будете двигаться гораздо медленнее. (Рассуждая таким
образом, лучше всего было бы заранее тщательно вычислить путь!) Во всяком случае,
давайте попытаемся показать, что окончательное решение задачи — это путь ![]() , который занимает
из всех возможных наименьшее время. Если этот путь кратчайший по времени, то
любой другой окажется длиннее. Поэтому если отложить на графике зависимость времени
от положения точки
, который занимает
из всех возможных наименьшее время. Если этот путь кратчайший по времени, то
любой другой окажется длиннее. Поэтому если отложить на графике зависимость времени
от положения точки ![]() , получится кривая, похожая на
изображенную на фиг. 26.5, где точка
, получится кривая, похожая на
изображенную на фиг. 26.5, где точка ![]() соответствует наименьшему времени.
Это означает, что для точек
соответствует наименьшему времени.
Это означает, что для точек ![]() вблизи
вблизи ![]() в первом приближении время
прохождения практически одинаковое, гак как в точке
в первом приближении время
прохождения практически одинаковое, гак как в точке ![]() наклон кривой равен нулю.
Итак, наш способ найти искомый путь сводится к требованию, чтобы при небольшом
изменении положения точки время прохождения не менялось. (Конечно, возникнут
бесконечно малые изменения времени второго порядка, и они должны быть
положительными при смещении в обе стороны от точки
наклон кривой равен нулю.
Итак, наш способ найти искомый путь сводится к требованию, чтобы при небольшом
изменении положения точки время прохождения не менялось. (Конечно, возникнут
бесконечно малые изменения времени второго порядка, и они должны быть
положительными при смещении в обе стороны от точки ![]() .) Возьмем близкую точку
.) Возьмем близкую точку ![]() , вычислим время
прохождения на пути
, вычислим время
прохождения на пути ![]() и сравним его со старым путем
и сравним его со старым путем ![]() . Сделать это очень
просто. Конечно, нужно еще, чтобы разность времен стремилась к нулю для малых
расстояний
. Сделать это очень
просто. Конечно, нужно еще, чтобы разность времен стремилась к нулю для малых
расстояний ![]() .
Обратимся сначала к пути по суше. Если мы опустим перпендикуляр
.
Обратимся сначала к пути по суше. Если мы опустим перпендикуляр ![]() , то легко увидим,
что наш путь стал короче на длину
, то легко увидим,
что наш путь стал короче на длину ![]() . Можно сказать, что это расстояние мы
выиграли. С другой стороны, опустив перпендикуляр
. Можно сказать, что это расстояние мы
выиграли. С другой стороны, опустив перпендикуляр ![]() , мы увидим, что в воде приходится
проплыть дополнительное расстояние
, мы увидим, что в воде приходится
проплыть дополнительное расстояние ![]() . В этом мы проиграли. С точки зрения
экономии времени выигрывается время на отрезке
. В этом мы проиграли. С точки зрения
экономии времени выигрывается время на отрезке ![]() , но теряется на отрезке
, но теряется на отрезке ![]() . Эти два интервала
времени должны быть равны, так как в первом приближении полное время
прохождения не меняется. Предположив, что скорость в воде равна скорости в
воздухе, умноженной на
. Эти два интервала
времени должны быть равны, так как в первом приближении полное время
прохождения не меняется. Предположив, что скорость в воде равна скорости в
воздухе, умноженной на ![]() , получим
, получим
![]() . (26.3)
. (26.3)

Фигура 26.4. Иллюстрация принципа Ферма для случая преломления

Фигура 26.5. Наименьшее время получается при выборе точки ![]() . Соседние точки
приводят примерно к такому же времени прохождения
. Соседние точки
приводят примерно к такому же времени прохождения
Поэтому мы видим, что
если нам удалось правильно выбрать точку ![]() или мы сократили на длину общей
гипотенузы
или мы сократили на длину общей
гипотенузы ![]() и
заметили, что
и
заметили, что
![]() и
и ![]() ,
,
то мы получим
![]() . (26.4)
. (26.4)
Отсюда видно, что при
отношении скоростей, равном ![]() , свет должен двигаться из одной точки
в другую по такому пути, чтобы отношение синусов
, свет должен двигаться из одной точки
в другую по такому пути, чтобы отношение синусов ![]() и
и ![]() было равно отношению скоростей в двух
средах.
было равно отношению скоростей в двух
средах.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
- § 4. Диаграмма цветности
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии