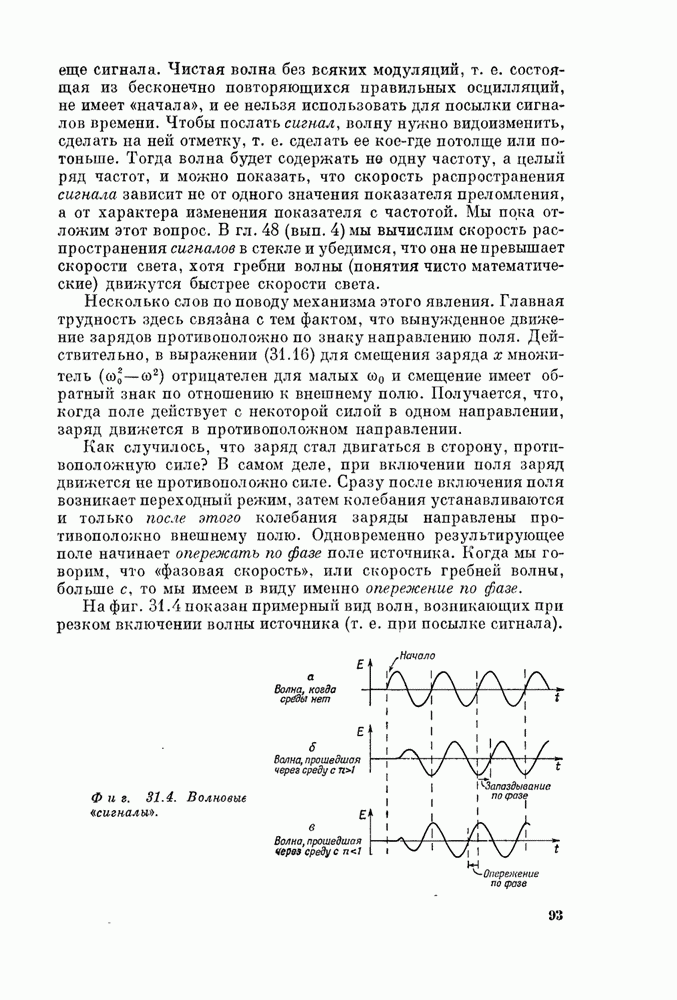
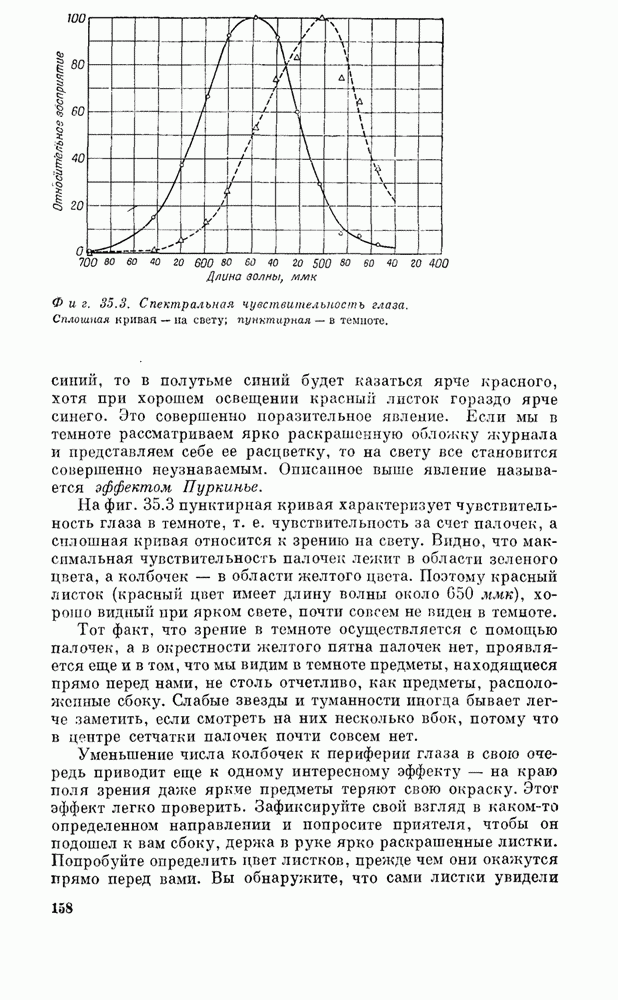
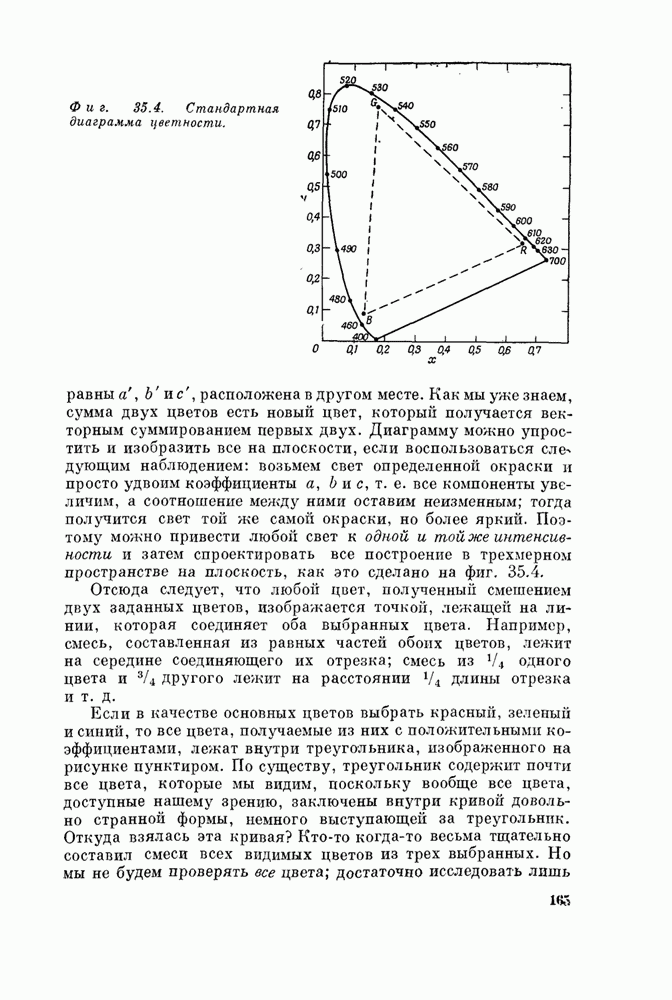
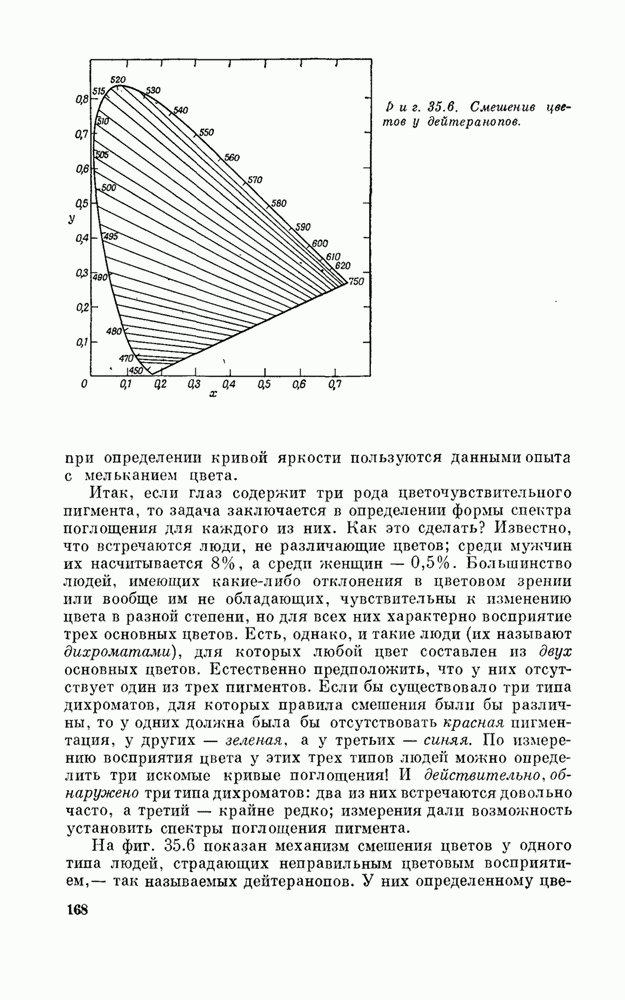
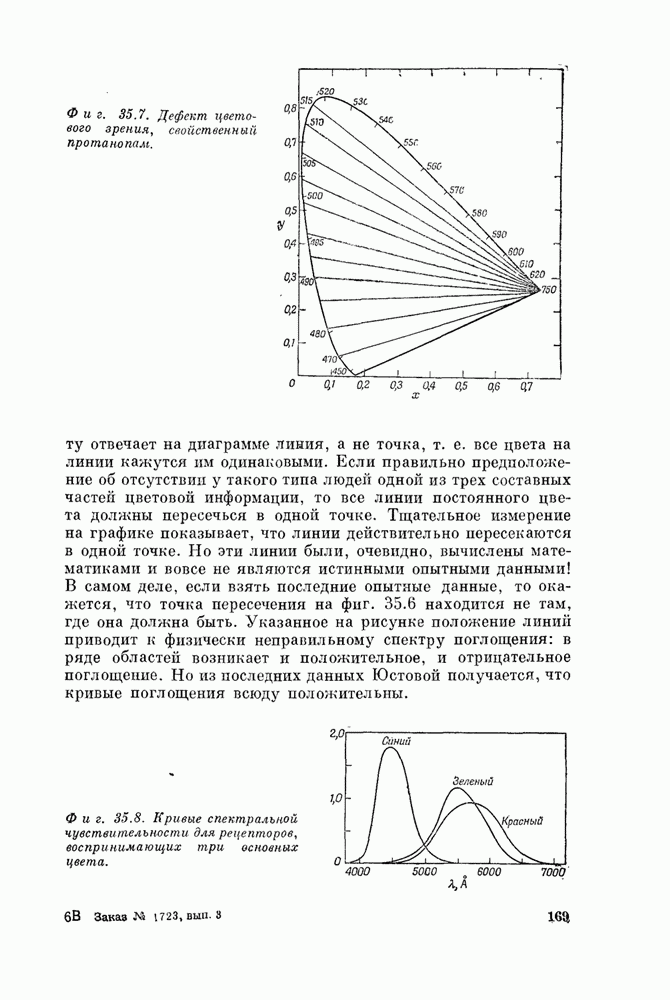
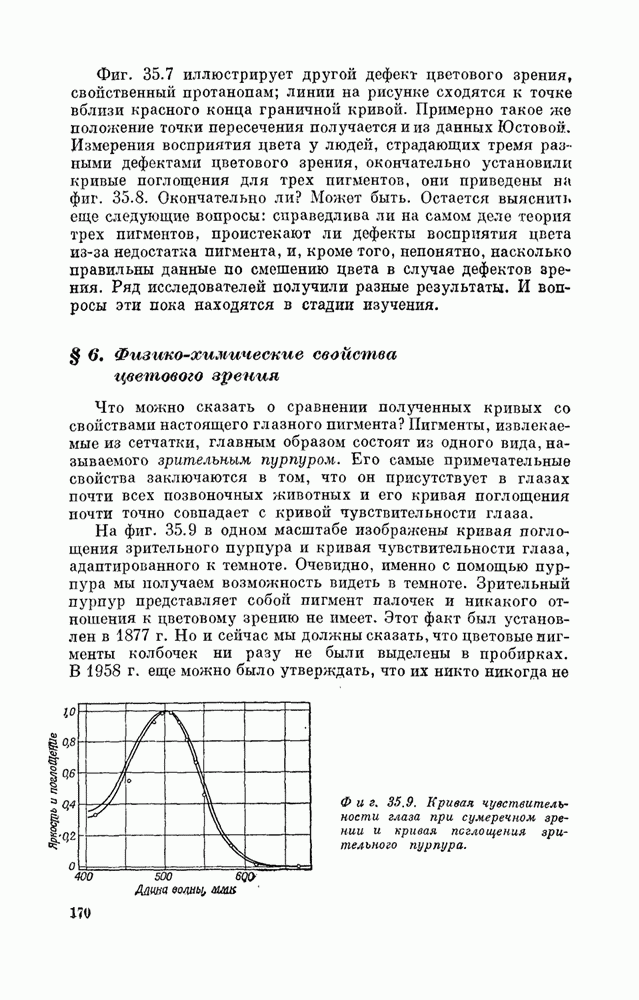
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Измерение положения и импульса
Чтобы понять, почему в квантовой механике появляется неопределенность в положении и (или) в импульсе, рассмотрим два примера. Мы уже видели раньше, что если бы этого не было, если бы можно было параллельно измерять и местонахождение, и импульс какого-то тела, то возник бы парадокс. К счастью, парадокса не возникает, а то обстоятельство, что неопределенность естественным образом вытекает из волновой картины, свидетельствует, что все здесь взаимосвязано.
Вот первый пример, показывающий связь импульса и координаты в условиях,
которые легко себе представить. Пусть сквозь единственную щель в экране
проникают частицы, пришедшие издалека и обладающие определенной энергией.
Движутся все они горизонтально (фиг. 38.2). Сосредоточим наше внимание на
вертикальной составляющей импульса. У каждой из этих частиц имеется (в обычном
классическом смысле) горизонтальная составляющая импульса определенной величины
![]() .
Вертикальная составляющая импульса
.
Вертикальная составляющая импульса ![]() (до того, как частица пройдет сквозь
прорезь) также в классическом смысле хороню известна: частицы не движутся ни
вверх, ни вниз, потому что их источник очень удален, значит, вертикальная
составляющая импульса частицы в точности равна нулю. А теперь предположим, что
ширина щели раина
(до того, как частица пройдет сквозь
прорезь) также в классическом смысле хороню известна: частицы не движутся ни
вверх, ни вниз, потому что их источник очень удален, значит, вертикальная
составляющая импульса частицы в точности равна нулю. А теперь предположим, что
ширина щели раина ![]() . Когда частика пройдет через щель,
то ее вертикальная координата
. Когда частика пройдет через щель,
то ее вертикальная координата ![]() определится с хорошей точностью
определится с хорошей точностью ![]() . Это значит, что
неопределенность в положении частицы
. Это значит, что
неопределенность в положении частицы ![]() будет порядка
будет порядка ![]() . Может, вы захотите
сказать, что
. Может, вы захотите
сказать, что ![]() ,
потому что импульс частиц, мол, точно горизонтален? Но это не так. Это прежде
мы знали, что Импульс имеет только горизонтальную составляющую, а теперь мы
этого уже не знаем. Перед тем как частица проникла сквозь щель, мы не знали ее
вертикальной координаты. После того как частица проникла сквозь щель, мы узнали
ее вертикальную координату, но потеряли информацию об ее вертикальной составляющей
импульса! Почему? Да потому, что, согласно волновой теории, происходит
отклонение, или дифракция, волн, проникших сквозь щель, подобно тому как это
бывает со светом. Поэтому есть конечная вероятность того, что частицы, пройдя
сквозь щель, не пойдут прямо вперед. Вся картина распространения расплывается
за счет дифракции, и угол этого расширения (угол, под которым виден первый
минимум) есть мера неопределенности направления частицы.
,
потому что импульс частиц, мол, точно горизонтален? Но это не так. Это прежде
мы знали, что Импульс имеет только горизонтальную составляющую, а теперь мы
этого уже не знаем. Перед тем как частица проникла сквозь щель, мы не знали ее
вертикальной координаты. После того как частица проникла сквозь щель, мы узнали
ее вертикальную координату, но потеряли информацию об ее вертикальной составляющей
импульса! Почему? Да потому, что, согласно волновой теории, происходит
отклонение, или дифракция, волн, проникших сквозь щель, подобно тому как это
бывает со светом. Поэтому есть конечная вероятность того, что частицы, пройдя
сквозь щель, не пойдут прямо вперед. Вся картина распространения расплывается
за счет дифракции, и угол этого расширения (угол, под которым виден первый
минимум) есть мера неопределенности направления частицы.

Фигура 38.2. Дифракция частиц, проходящих сквозь щель.
Каким образом происходит расплывание изображения в ширину? Расплывание
означает, что существует некая вероятность того, что частица отправится вверх
или вниз, т. е. приобретет компоненту импульса, направленную вверх или вниз.
(Мы говорим и о вероятности и о частице, потому что дифракционную картину можно
обнаружить с помощью счетчика частиц, а когда счетчик регистрирует частицу,
скажем, в точке ![]() на
фиг. 38.2, то он регистрирует частицу целиком. А это значит в классическом
смысле, что частица имеет вертикальный импульс, направляющий ее из щели прямо в
точку
на
фиг. 38.2, то он регистрирует частицу целиком. А это значит в классическом
смысле, что частица имеет вертикальный импульс, направляющий ее из щели прямо в
точку ![]() .)
.)
Чтобы примерно представить себе степень расплывания импульса, напишем,
что вертикальный импульс ![]() размазан на
размазан на ![]() , где
, где ![]() — горизонтальный импульс.
Чему же равно
— горизонтальный импульс.
Чему же равно ![]() в
размазанной картине? Известно, что первый минимум наблюдается при угле
в
размазанной картине? Известно, что первый минимум наблюдается при угле ![]() таком, что в этом
направлении волна от дальнего края щели должна отстать на одну свою длину от
волны от ближнего края (мы об этом уже говорили в гл. 30). Стало быть,
таком, что в этом
направлении волна от дальнего края щели должна отстать на одну свою длину от
волны от ближнего края (мы об этом уже говорили в гл. 30). Стало быть, ![]() равно
равно ![]() , и тем самым
, и тем самым ![]() в этом
эксперименте равно
в этом
эксперименте равно ![]() . Чем меньше будет
. Чем меньше будет ![]() , чем точнее будет
определяться положение частицы, тем шире будет дифракционная картина.
Вспомните, что когда мы закрывали щели в эксперименте с микроволнами, то
интенсивность в стороне от щели возрастала. Значит, чем уже щель, тем шире
становится картина дифракции, тем правдоподобнее, что мы обнаружим у частицы
импульс, направленный в сторону. И неопределенность в вертикальном импульсе,
действительно, обратно пропорциональна неопределенности в
, чем точнее будет
определяться положение частицы, тем шире будет дифракционная картина.
Вспомните, что когда мы закрывали щели в эксперименте с микроволнами, то
интенсивность в стороне от щели возрастала. Значит, чем уже щель, тем шире
становится картина дифракции, тем правдоподобнее, что мы обнаружим у частицы
импульс, направленный в сторону. И неопределенность в вертикальном импульсе,
действительно, обратно пропорциональна неопределенности в ![]() , потому что их
произведение равно
, потому что их
произведение равно ![]() .
.
Но ![]() —
это длина волны, а
—
это длина волны, а ![]() — импульс, и в соответствии с
квантовой механикой их произведение — это постоянная Планка
— импульс, и в соответствии с
квантовой механикой их произведение — это постоянная Планка ![]() . Получается, что
произведение неопределенностей в вертикальном импульсе и в вертикальной
координате есть величина порядка
. Получается, что
произведение неопределенностей в вертикальном импульсе и в вертикальной
координате есть величина порядка ![]() :
:
![]() (38.3)
(38.3)
Мы не можем приготовить систему, в которой положение частицы по вертикали
было бы известно, и в то же время предсказывать с определенностью, превышающей ![]() , насколько ее
движение отклонится от вертикали. Неопределенность в вертикальном импульсе
всегда больше
, насколько ее
движение отклонится от вертикали. Неопределенность в вертикальном импульсе
всегда больше ![]() ,
если
,
если ![]() —
неопределенность, с какой мы знаем положение частицы.
—
неопределенность, с какой мы знаем положение частицы.
Некоторые люди утверждают, что в квантовой механике все неправильно. Когда, говорят они, частица приближалась слева, ее вертикальный импульс был равен нулю. А когда она прошла через щель, стало известно ее положение. И то, и другое может быть определено с любой точностью.
Совершенно верно. Мы можем зарегистрировать частицу и определить, каково ее положение и каким должен был быть ее импульс, чтобы она попала туда, куда она попала. Это все верно. Но соотношение неопределенностей (38.3) ничего общего с этим не имеет. Уравнение (38.3) относится к возможности предсказания, а не к замечаниям о том, что произошло в прошлом. Какая польза в том, что мы скажем: «Я знал, каков был импульс до прохода частицы сквозь щель, а теперь узнал к тому же и координату»? Ведь теперь-то знание об импульсе частицы уже утеряно. Раз она прошла сквозь щель, то мы уже не можем больше предсказывать ее вертикальный импульс. Речь идет о теории, способной к предсказаниям, а не об измерениях после того, как все завершилось. Мы и обсуждаем вопрос о том, что можно предвидеть.
Попробуем теперь по-иному подойти к этим вещам. Приведем другой пример того же явления, на этот раз с более подробными количественными оценками. Прежде мы измеряли импульс классическим способом: мы рассматривали направление, скорость, углы, и тому подобное; в этом заключался способ получения импульса путем классического анализа. Но раз импульс связан с волновым числом, то в природе существует и другой, совершенно иной путь измерения импульса частиц (все равно, фотона или любой другой), не имеющий классического аналога. В нем используется уравнение (38.2) и просто измеряется длина волны. Давайте попробуем таким способом измерить импульс.
Пусть имеется решетка со множеством линий (фиг. 38.3), на которую
направлен пучок частиц. Мы неоднократно рассматривали эту задачу: когда у
частиц есть определенный импульс, то вследствие интерференции в некотором
направлении возникает очень резкий максимум. Мы также говорили о том, насколько
точно можно определить этот импульс, т. е. какова разрешающая сила решетки. Мы
не будем заново это все выводить, а сошлемся на гл. 30; там мы выяснили, что
относительная неопределенность в длине волны, связанная с данной решеткой,
равна ![]() ,
где
,
где ![]() —
количество линий решетки, а
—
количество линий решетки, а ![]() — порядок дифракционного максимума.
Иначе говоря,
— порядок дифракционного максимума.
Иначе говоря,
![]() (38.4)
(38.4)

Фигура 38.3. Определение импульса с помощью дифракционной решетки
Перепишем эту формулу в виде
![]() (38.5)
(38.5)
где расстояние ![]() показано на фиг. 38.3. Это —
разность двух расстояний: расстояния, которое должна пройти волна (или частица),
отразившись от нижней части решетки, и расстояния, которое нужно пройти,
отразившись от верха решетки.
показано на фиг. 38.3. Это —
разность двух расстояний: расстояния, которое должна пройти волна (или частица),
отразившись от нижней части решетки, и расстояния, которое нужно пройти,
отразившись от верха решетки.
Другими словами, волны, образующие дифракционный максимум, — это волны,
приходящие от разных частей решетки. Первыми прибывают волны, вышедшие снизу — это
начало цуга волн, а потом следуют дальнейшие части цуга, от средних частей
решетки, пока не придут волны от верха: точка цуга, удаленная от его начала на
расстояние ![]() .
Значит, чтобы получить в спектре резкую линию, отвечающую определенному
импульсу [с неопределенностью, даваемой формулой (38.4)], для этого нужен цуг
волн длиной
.
Значит, чтобы получить в спектре резкую линию, отвечающую определенному
импульсу [с неопределенностью, даваемой формулой (38.4)], для этого нужен цуг
волн длиной ![]() .
Если цуг чересчур короток (короче
.
Если цуг чересчур короток (короче ![]() ), то не вся решетка будет
действовать. Волны, образующие спектр, будут отражаться при этом только от
небольшого куска решетки, и решетка не будет хорошо работать — получится
сильное размытие по углу. Чтобы его сузить, надо использовать всю ширину
решетки так, чтобы хотя бы на одно мгновение весь цуг волн улегся одновременно
на решетке и рассеялся ото всех ее частей. Потому-то длина цуга должна быть
равна
), то не вся решетка будет
действовать. Волны, образующие спектр, будут отражаться при этом только от
небольшого куска решетки, и решетка не будет хорошо работать — получится
сильное размытие по углу. Чтобы его сузить, надо использовать всю ширину
решетки так, чтобы хотя бы на одно мгновение весь цуг волн улегся одновременно
на решетке и рассеялся ото всех ее частей. Потому-то длина цуга должна быть
равна ![]() ;
тогда только неопределенность в длине волны окажется меньше, чем указано
формулой (38.5). Заметим, что
;
тогда только неопределенность в длине волны окажется меньше, чем указано
формулой (38.5). Заметим, что
![]() (38.6)
(38.6)
поэтому
![]() (38.7)
(38.7)
где ![]() —
длина цуга волн.
—
длина цуга волн.
Это означает, что когда цуг волн короче ![]() , то неопределенность в волновом
числе превосходит
, то неопределенность в волновом
числе превосходит ![]() . Иначе говоря, неопределенность в
волновом числе, умноженная на длину волнового цуга (назовем ее на минутку
. Иначе говоря, неопределенность в
волновом числе, умноженная на длину волнового цуга (назовем ее на минутку ![]() ), больше
), больше ![]() . Мы назвали ее
. Мы назвали ее ![]() : потому, что это
как раз неопределенность в положении частицы. Если цуг волн тянется только на
конечном промежутке, то лишь там мы и можем обнаружить частицу с
неопределенностью
: потому, что это
как раз неопределенность в положении частицы. Если цуг волн тянется только на
конечном промежутке, то лишь там мы и можем обнаружить частицу с
неопределенностью ![]() . Это свойство волн (тот факт, что
произведение длины цуга волн на неопределенность в волновом числе, связанном с
этим цугом, не меньше
. Это свойство волн (тот факт, что
произведение длины цуга волн на неопределенность в волновом числе, связанном с
этим цугом, не меньше ![]() ) опять-таки хорошо знакомо всем, кто
занимался волнами. И никакого отношения к волновой механике оно не имеет.
Просто нельзя очень точно подсчитать число волн в конечной их веренице.
) опять-таки хорошо знакомо всем, кто
занимался волнами. И никакого отношения к волновой механике оно не имеет.
Просто нельзя очень точно подсчитать число волн в конечной их веренице.
Объяснить это можно и по-другому. Пусть длина цуга волн ![]() . Так как на
концах цуга волны спадают (как на фиг. 38.1), то количество волн на длине
. Так как на
концах цуга волны спадают (как на фиг. 38.1), то количество волн на длине ![]() известно с
точностью порядка
известно с
точностью порядка ![]() . Но число волн на длине
. Но число волн на длине ![]() равно
равно ![]() . Значит,
неопределенность в
. Значит,
неопределенность в ![]() равна
равна ![]() . Опять получилась формула (38.7) как
простое свойство всяких волн. Это остается верным всегда: и для волн в
пространстве, когда
. Опять получилась формула (38.7) как
простое свойство всяких волн. Это остается верным всегда: и для волн в
пространстве, когда ![]() есть количество радиан на
есть количество радиан на ![]() , a,
, a, ![]() — длина цуга, и
для волн во времени, когда
— длина цуга, и
для волн во времени, когда ![]() есть число колебаний в
есть число колебаний в ![]() , а
, а ![]() — «длина» во
времени того же цуга. Иначе говоря, если цуг волн длится только конечное время
— «длина» во
времени того же цуга. Иначе говоря, если цуг волн длится только конечное время ![]() , то
неопределенность в частоте дается формулой
, то
неопределенность в частоте дается формулой
![]() (38.8)
(38.8)
Мы все время старались подчеркнуть, что это свойство самих волн, что все
это хорошо известно, например в теории звука. А квантовомеханические применения
этих свойств опираются на толкование волнового числа как меры импульса частицы
по правилу ![]() ,
так что (38.7) уже утверждает, что
,
так что (38.7) уже утверждает, что ![]() . Это устанавливает предел
классическому представлению об импульсе. (Естественно, оно и должно быть как-то
подвергнуто ограничению, если мы собираемся изображать частицы как волны!) И
очень хорошо, что мы нашли правило, которое каким-то образом берется указать,
где нарушаются классические представления.
. Это устанавливает предел
классическому представлению об импульсе. (Естественно, оно и должно быть как-то
подвергнуто ограничению, если мы собираемся изображать частицы как волны!) И
очень хорошо, что мы нашли правило, которое каким-то образом берется указать,
где нарушаются классические представления.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
- § 4. Диаграмма цветности
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии