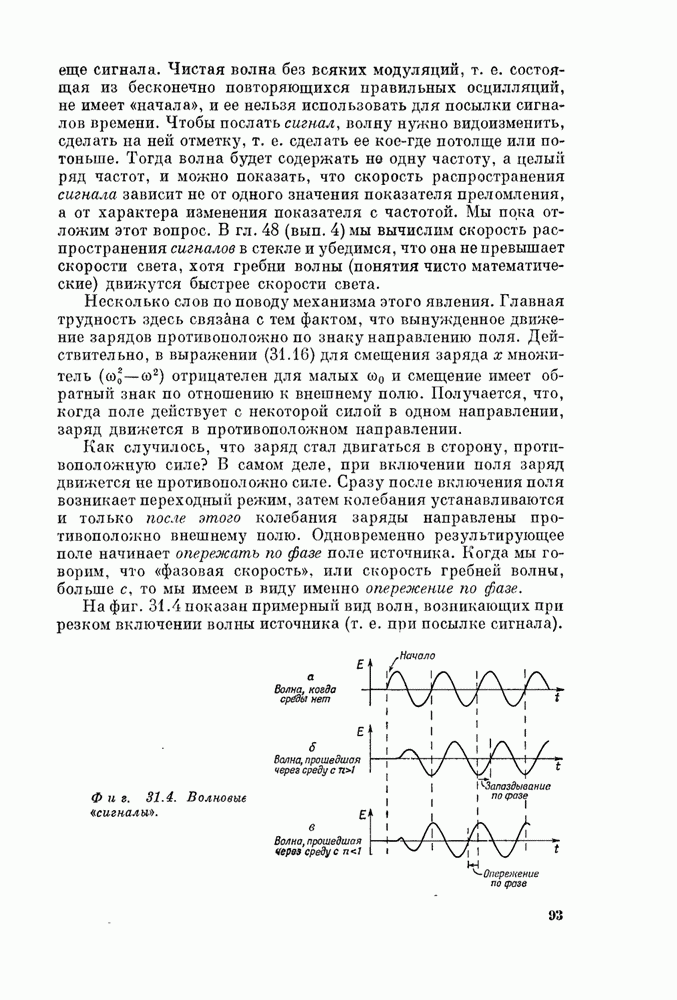
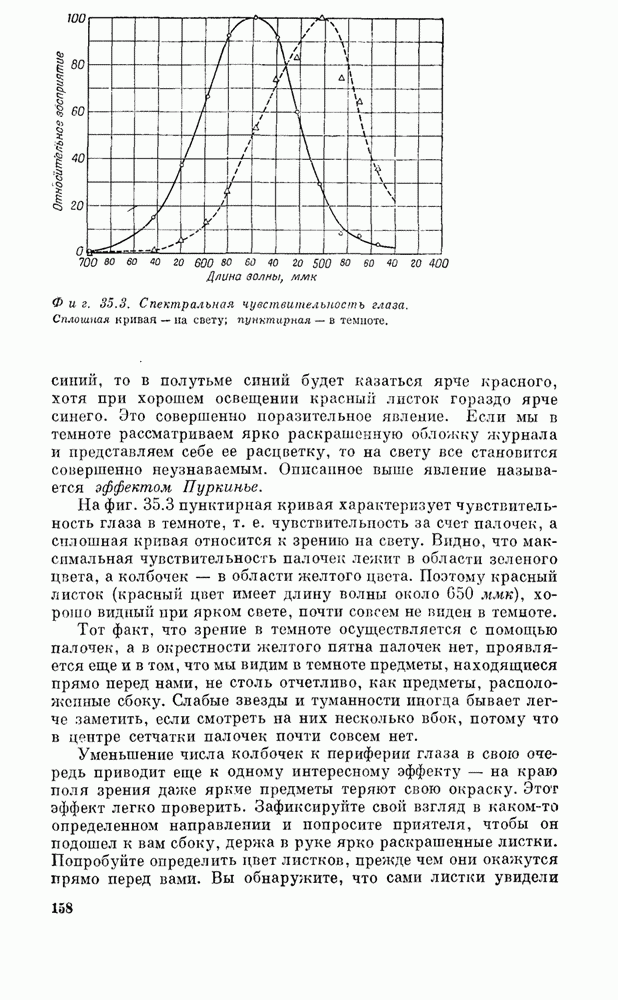
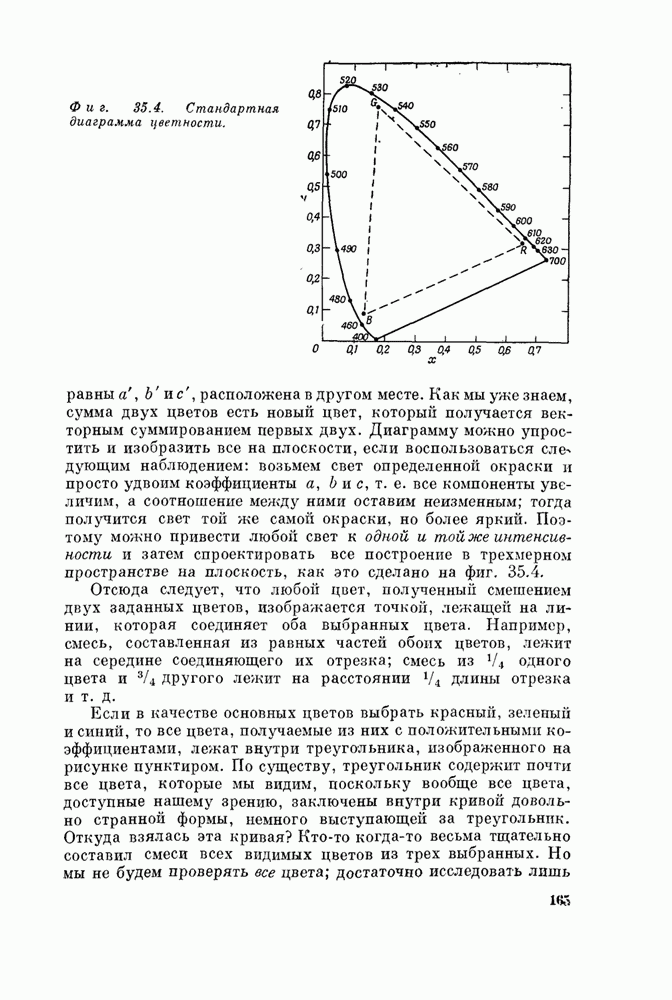
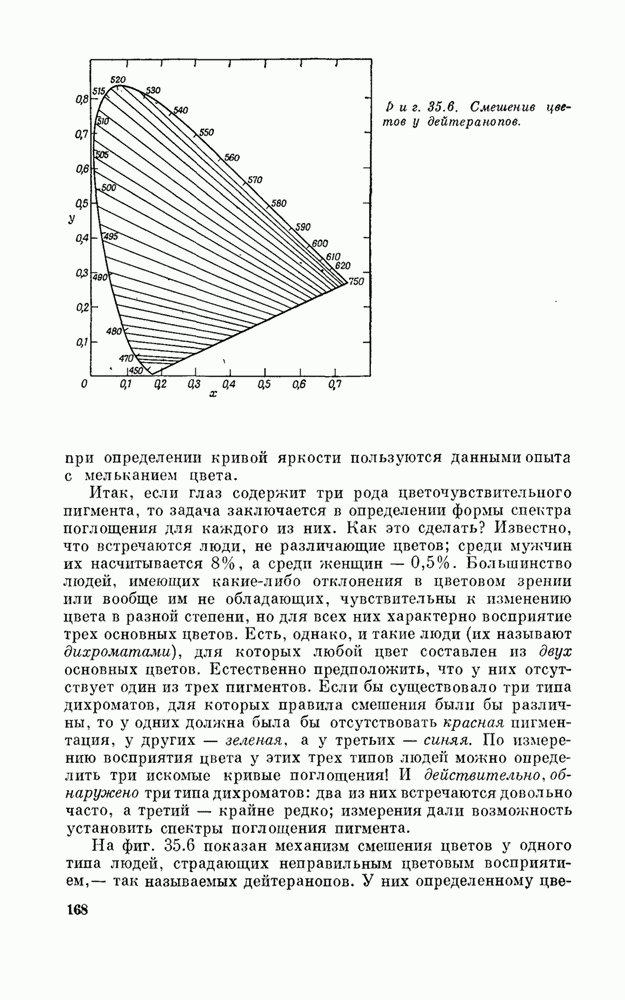
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Квантовый механизм
В заключение дадим очень
грубую картину того, что происходит на самом деле, как протекает весь процесс
распространения света с квантовомеханической точки зрения, которую сейчас
считают самой правильной (разумеется, наше описание будет носить лишь
качественный: характер). Исследуя свет на пути из ![]() в
в ![]() (см. фиг. 28.3), можно обнаружить,
что он вовсе не представляет собой волны. Лучи света, оказывается, состоят из
фотонов, которые можно реально зарегистрировать с помощью фотонного счетчика;
они заставляют его щелкать. Яркость света пропорциональна среднему числу
фотонов, пролетающему в 1сек, а нас интересует вероятность попадания фотона из
(см. фиг. 28.3), можно обнаружить,
что он вовсе не представляет собой волны. Лучи света, оказывается, состоят из
фотонов, которые можно реально зарегистрировать с помощью фотонного счетчика;
они заставляют его щелкать. Яркость света пропорциональна среднему числу
фотонов, пролетающему в 1сек, а нас интересует вероятность попадания фотона из ![]() в
в ![]() при отражении от
зеркала. Правило вычисления этой вероятности весьма необычно. Выберем
какой-нибудь путь и найдем время на этом пути; затем образуем комплексное число
или нарисуем маленький комплексный вектор
при отражении от
зеркала. Правило вычисления этой вероятности весьма необычно. Выберем
какой-нибудь путь и найдем время на этом пути; затем образуем комплексное число
или нарисуем маленький комплексный вектор ![]() , где угол
, где угол ![]() пропорционален времени.
Число оборотов вектора в секунду — это частота света. Возьмем теперь другой
путь, и пусть он занимает другое время; тогда соответствующий ему вектор
повернется на угол, отличный от первого (вспомним, что угол всегда пропорционален
времени). Переберем все возможные пути и сложим векторы для каждого из них,
тогда квадрат длины суммарного вектора определит вероятность прохождения фотона
из начальной точки в конечную!
пропорционален времени.
Число оборотов вектора в секунду — это частота света. Возьмем теперь другой
путь, и пусть он занимает другое время; тогда соответствующий ему вектор
повернется на угол, отличный от первого (вспомним, что угол всегда пропорционален
времени). Переберем все возможные пути и сложим векторы для каждого из них,
тогда квадрат длины суммарного вектора определит вероятность прохождения фотона
из начальной точки в конечную!

Фигура 26.14. Суммирование амплитуд вероятности на всевозможных соседних траекториях.
Покажем теперь, что
отсюда следует принцип наименьшего времени для зеркала. Возьмем все возможные
пути ![]() ,
, ![]() ,
, ![]() и т. д.,
изображенные на фиг. 26.3. Путь
и т. д.,
изображенные на фиг. 26.3. Путь ![]() вносит небольшой вклад, а соседний
путь
вносит небольшой вклад, а соседний
путь ![]() занимает
уже другое время, и его угол
занимает
уже другое время, и его угол ![]() поэтому другой. Пусть точка
поэтому другой. Пусть точка ![]() соответствует пути
с наименьшим временем, тогда при небольшом изменении пути время не меняется.
Точнее, сначала время заметно менялось, но с приближением к точке
соответствует пути
с наименьшим временем, тогда при небольшом изменении пути время не меняется.
Точнее, сначала время заметно менялось, но с приближением к точке ![]() оно меняется все
меньше и меньше (фиг. 26.14). Таким образом, векторы, которые мы складываем,
проходят вблизи
оно меняется все
меньше и меньше (фиг. 26.14). Таким образом, векторы, которые мы складываем,
проходят вблизи ![]() почти
под одним и тем же углом, а затем времена начинают постепенно расти, векторы
поворачиваются и т. д. В результате получается тугой клубок векторов. Полная
вероятность есть расстояние от одного конца до другого, возведенное в квадрат.
Почти весь вклад в эту суммарную вероятность вносит область, где векторы идут в
одном направлении (с одной и той же фазой). Вклады от путей с разными временами
взаимно сокращаются, потому что векторы направлены в разные стороны. Вот
почему, если закрыть края зеркала, оно будет отражать почти точно так же, как и
раньше, поскольку в приведенной выше процедуре это соответствует отбрасыванию
части векторов внутри спиральных концов диаграммы, а для света это мало что
изменит. Таково соответствие между современной теорией фотонов с ее понятием
вероятности прохождения, зависящей от суммирования векторов, и принципом
наименьшего времени.
почти
под одним и тем же углом, а затем времена начинают постепенно расти, векторы
поворачиваются и т. д. В результате получается тугой клубок векторов. Полная
вероятность есть расстояние от одного конца до другого, возведенное в квадрат.
Почти весь вклад в эту суммарную вероятность вносит область, где векторы идут в
одном направлении (с одной и той же фазой). Вклады от путей с разными временами
взаимно сокращаются, потому что векторы направлены в разные стороны. Вот
почему, если закрыть края зеркала, оно будет отражать почти точно так же, как и
раньше, поскольку в приведенной выше процедуре это соответствует отбрасыванию
части векторов внутри спиральных концов диаграммы, а для света это мало что
изменит. Таково соответствие между современной теорией фотонов с ее понятием
вероятности прохождения, зависящей от суммирования векторов, и принципом
наименьшего времени.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
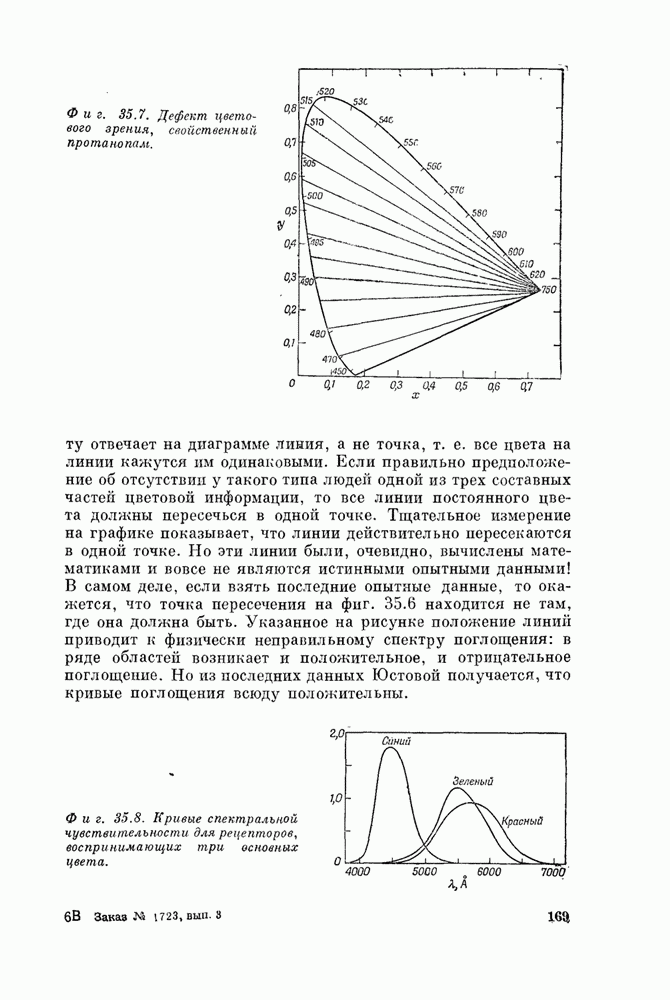
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
- § 4. Диаграмма цветности
- § 5. Механизм цветового зрения
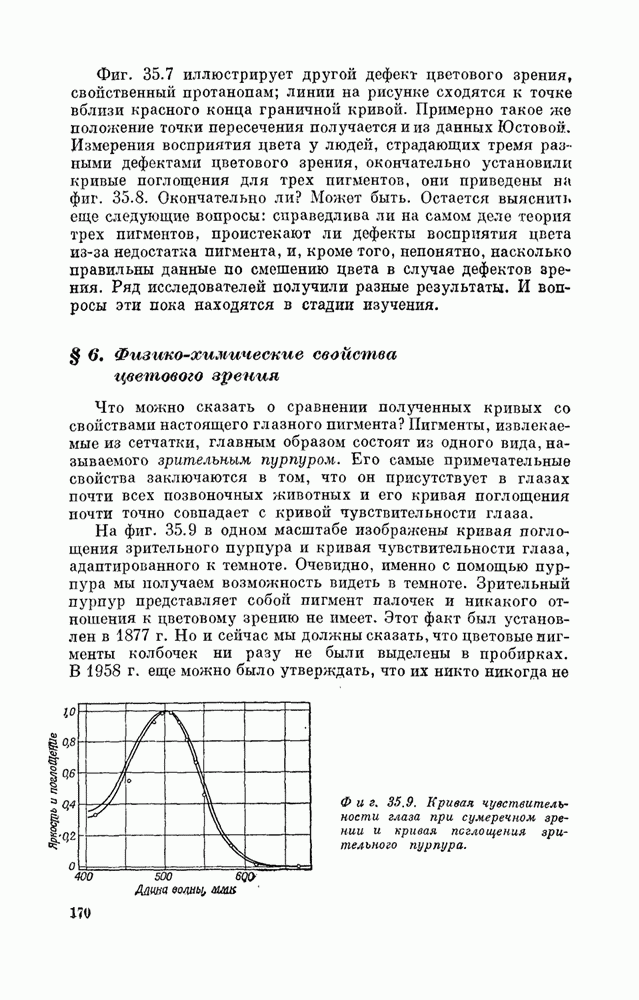
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии