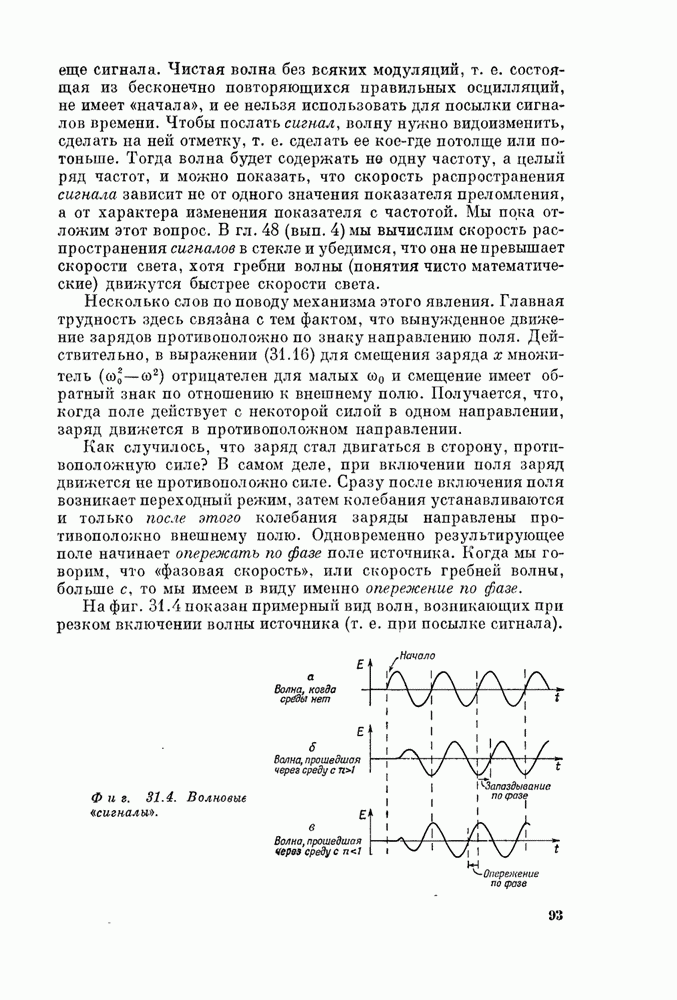
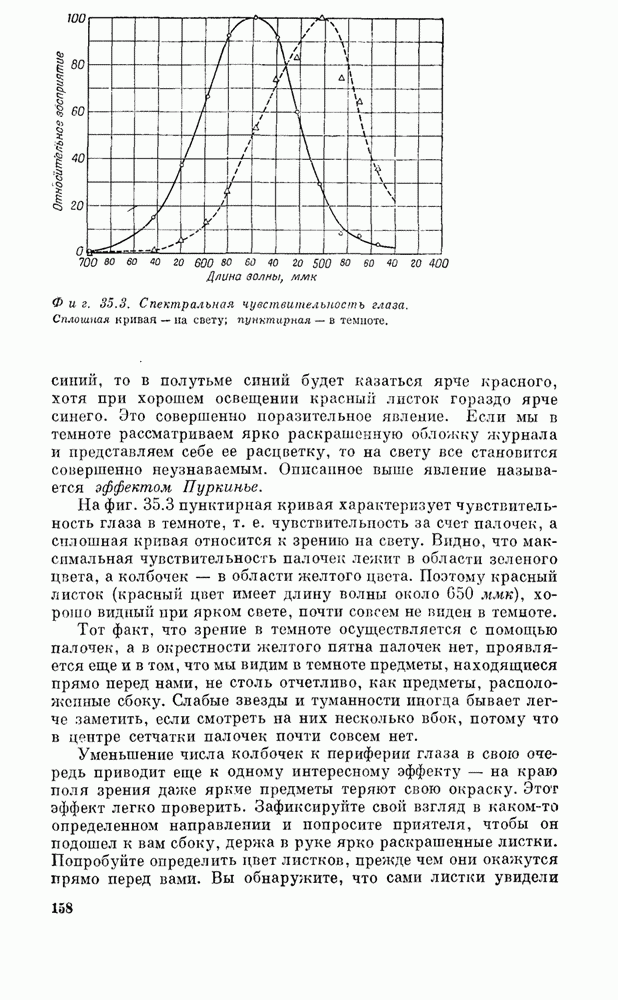
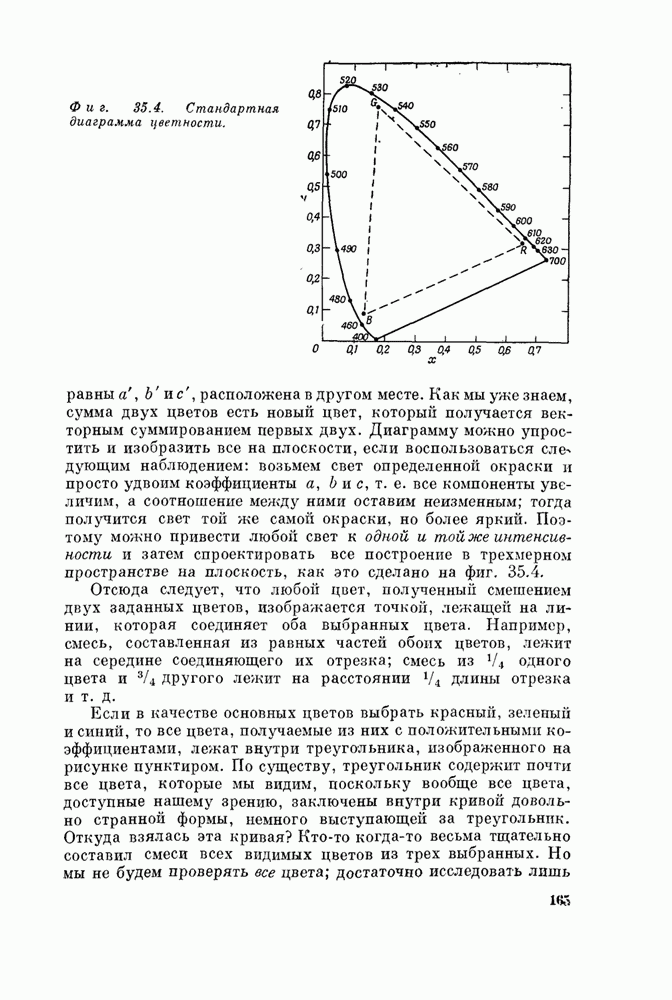
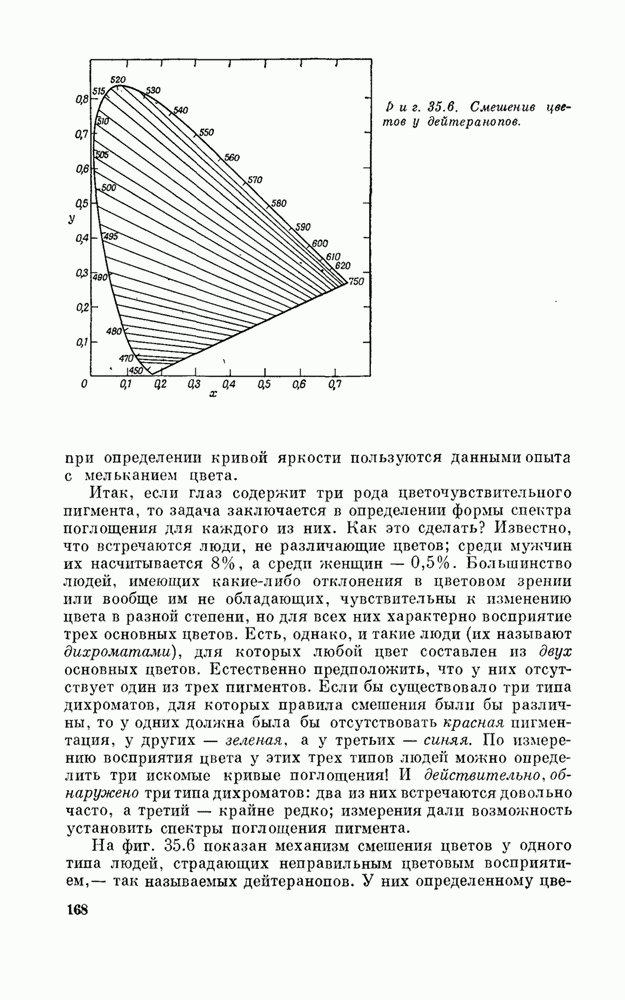
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 27. Геометрическая оптика
§ 1. Введение
В этой главе мы рассмотрим некоторые применения изложенных ранее принципов устройству простейших оптических систем, используя приближение геометрической оптики. При конструировании многих оптических приборов это приближение оказывается особенно полезным. Геометрическая оптика и очень проста, и очень сложна. Я хочу этим сказать, что уже поверхностное изучение геометрической оптики в школе позволяет с помощью очень простых правил составлять грубые схемы приборов; если же мы хотим при этом учитывать искажения в линзах и прочие тонкости, то задача становится слишком сложной даже для студентов вашего курса! Если кому-нибудь действительно понадобится точно спроектировать линзу, учитывая аберрацию, то лучше всего обратиться к специальным руководствам или просто проследить путь лучей через разные поверхности (как это сделать — сказано в книгах) и, пользуясь законом преломления, определить направление вышедших из линзы пучков и выяснить, насколько хорошее изображение они создают. Считалось, что это слишком длинная процедура, но сейчас, когда мы вооружены вычислительными машинами, этот способ вполне хорош. Сформулировав задачу математически, легко подсчитать пути всех лучей. Словом, дело это простое и не требует новых принципов. Кроме того, законы и элементарной и специальной оптики фактически неприменимы в других областях, поэтому нам не было бы необходимости чересчур подробно изучать предмет, если бы не одно важное исключение.

Фигура 27.1. Треугольник, высота которого ![]() меньше основания
меньше основания ![]() , а гипотенуза
, а гипотенуза ![]() больше основания
больше основания
Оказалось, что наиболее современная и абстрактная теория геометрической оптики, разработанная Гамильтоном, имеет весьма важные приложения в механике, причем в механике она имеет даже большее значение, чем в оптике, поэтому пусть его занимается курс аналитической механики. А пока, понимая, что геометрическая оптика интересна только сама по себе, мы перейдем к изучению элементарных свойств оптических систем на основе принципов, изложенных в предыдущей главе.
Для дальнейшего нам
понадобится одна геометрическая формула: пусть дан треугольник, высота которого
![]() мала, а
основание
мала, а
основание ![]() велико;
тогда гипотенуза
велико;
тогда гипотенуза ![]() (фиг.
27.1) больше основания (нам нужно это знать, чтобы вычислить разность времен на
двух различных путях света). Насколько гипотенуза больше основания? Мы можем
найти разность
(фиг.
27.1) больше основания (нам нужно это знать, чтобы вычислить разность времен на
двух различных путях света). Насколько гипотенуза больше основания? Мы можем
найти разность ![]() несколькими
способами. Например,
несколькими
способами. Например, ![]() или
или ![]() . Но
. Но ![]() , а
, а ![]() . Таким образом,
. Таким образом,
![]() . (27.1)
. (27.1)
Вот и все, что нам нужно знать из геометрии для изучения изображений, получаемых с помощью кривых поверхностей!
| << Предыдущий параграф | Следующий параграф >> |
- Глава 26 Оптика Принцип наименьшего времени
- § 1. Свет
- § 2. Отражение и преломление
- § 3. Принцип наименьшего времени Ферма
- § 4. Применения принципа Ферма
- § 5. Более точная формулировка принципа Ферма
- § 6. Квантовый механизм
- Глава 27. Геометрическая оптика
- § 1. Введение
- § 2. Фокусное расстояние для сферической поверхности
- § 3. Фокусное расстояние линзы
- § 4. Увеличение
- § 5. Сложные линзы
- § 6. Аберрация
- § 7. Разрешающая способность
- Глава 28 Электромагнитное излучение
- § 1. Электромагнетизм
- § 2. Излучение
- § 3. Дипольный излучатель
- § 4. Интерференции
- Глава 29. Интерференция
- § 1. Электромагнитные волны
- § 2. Энергия излучения
- § 3. Синусоидальные волны
- § 4. Два дипольных излучателя
- § 5. Математическое описание интерференции
- Глава 30. Дифракция
- § 1. Результирующее поле n одинаковых осцилляторов
- § 2. Дифракционная решетка
- § 3. Разрешающая способность дифракционной решетки
- § 4. Параболическая антенна
- § 5. Окрашенные пленки; кристаллы
- § 6. Дифракция на непрозрачном экране
- § 7. Поле системы осцилляторов, расположенных на плоскости
- Глава 31. Как возникает показатель преломления
- § 1. Показатель преломления
- § 2. Поле, излучаемое средой
- § 3. Дисперсия
- § 4. Поглощение
- § 5. Энергия световой волны
- § 6. Дифракция света на непрозрачном экране
- Глава 32. Радиационное затухание. Рассеяние света
- § 1. Радиационное сопротивление
- § 2. Интенсивность излучения
- § 3. Радиационное затухание
- § 4. Независимые источники
- § 5. Рассеяние света
- Глава 33. Поляризация
- § 1. Вектор электрического поля световой волны
- § 2. Поляризация рассеянного света
- § 3. Двойное лучепреломление
- § 4. Поляризаторы
- § 5. Оптическая активность
- § 6. Интенсивность отраженного света
- § 7. Аномальное преломление
- Глава 34. Релятивистские явления в излучении
- § 1. Движущиеся источники
- § 2. Определение «кажущегося» движения
- § 3. Синхротронное излучение
- § 4. Космическое синхротронное излучение
- § 5. Тормозное излучение
- § 6. Эффект Допплера
- § 7. Четырехвектор
- § 8. Аберрация
- § 9. Импульс световой волны
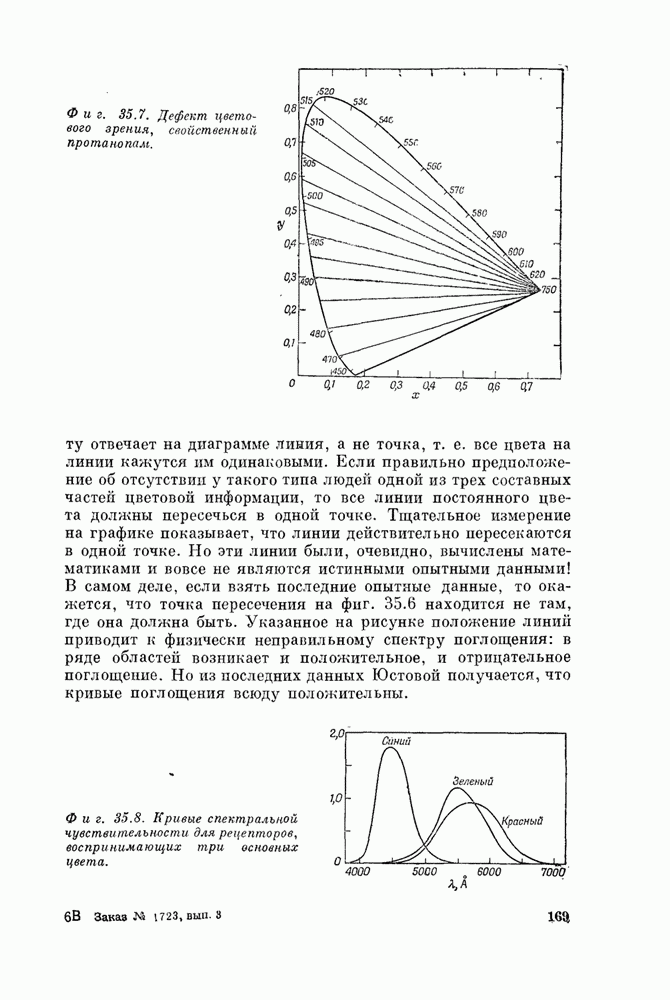
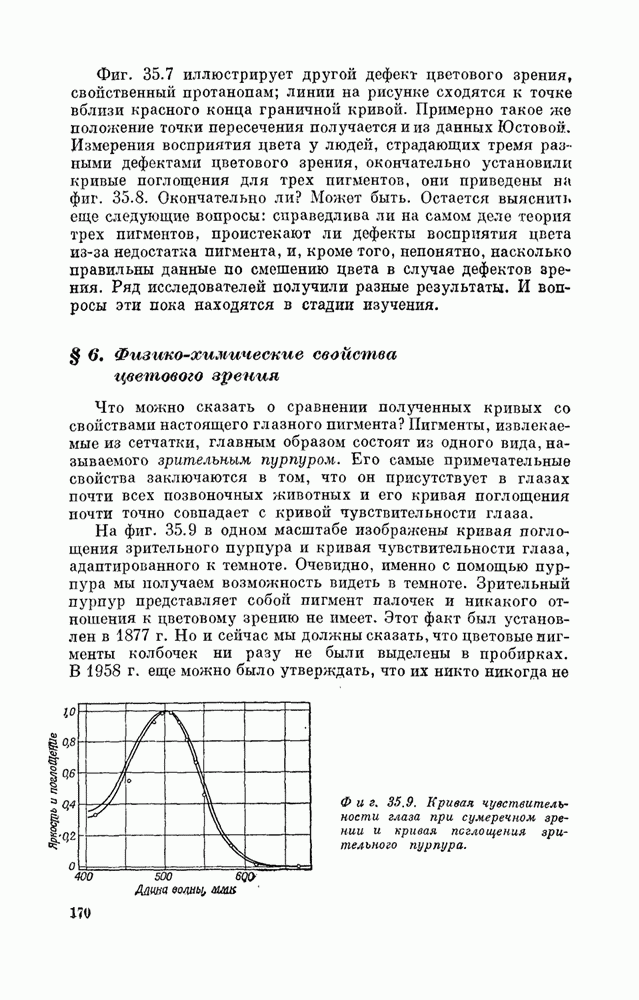
- Глава 35. Цветовое зрение
- § 1. Человеческий глаз
- § 2. Цвет зависит от интенсивности
- § 3. Измерение восприятия цвета
- § 4. Диаграмма цветности
- § 5. Механизм цветового зрения
- § 6. Физико-химические свойства цветового зрения
- Глава 36. Механизм зрения
- § 1. Ощущение цвета
- § 2. Физиология зрения
- § 3. Палочки
- § 4. Сложные глаза насекомых
- § 5. Другие типы глаз
- § 6. Нервные механизмы зрения
- Глава 37. Квантовое поведение
- § 1. Атомная механика
- § 2. Опыт с пулеметной стрельбой
- § 3. Опыт с волнами
- § 4. Опыт с электронами
- § 5. Интерференция электронных волн
- § 6. Как проследить за электроном?
- § 7. Начальные принципы квантовой механики
- § 8. Принцип неопределенности
- Глава 38. Соотношение между волновой и корпускулярной точками зрения
- § 1. Волны амплитуды вероятности
- § 2. Измерение положения и импульса
- § 3. Дифракция на кристалле
- § 4. Размер атома
- § 5. Уровни энергии
- § 6. Немного философии