§ 3. Дисперсия

Полученный нами результат очень интересен. Он дает не только показатель преломления, выраженный через атомные постоянные, но указывает, как меняется показатель преломления с частотой света . С помощью простого утверждения «свет движется с меньшей скоростью в прозрачной среде» мы никогда бы не смогли прийти к этому важному свойству. Нужно, конечно, еще знать число атомов в единице объема и собственную частоту атомов . Мы еще не умеем определять эти величины, поскольку они разные для разных материалов, а общую теорию по данному вопросу мы сейчас изложить не можем. Общая теория свойств различных веществ — их собственных частот и т. п.— формулируется на основе квантовой механики. Кроме того, свойства различных материалов и величина показателя преломления сильно меняются от материала к материалу, и поэтому вряд ли можно надеяться, что вообще удастся получить общую формулу, пригодную для всех веществ.

Тем не менее попробуем применить нашу формулу к разным средам. Прежде всего для большинства газов (например, для воздуха, большей части бесцветных газов, водорода, гелия и т. д.) собственные частоты колебаний электронов соответствуют ультрафиолетовому свету. Эти частоты много больше частот видимого света, т. е.  много больше , и в первом приближении можно пренебречь  по сравнению с . Тогда показатель преломления получается почти постоянным. Итак, для газов показатель преломления можно считать константой. Этот вывод справедлив также и для большинства других прозрачных сред, например для стекла. Взглянув более внимательно на наше выражение, можно заметить, что при увеличении  знаменатель уменьшается, а, следовательно, показатель преломления растет. Таким образом,  медленно увеличивается с ростом частоты. Для синего света показатель преломления больше, чем для красного. Именно поэтому синие лучи сильнее отклоняются призмой, чем красные.

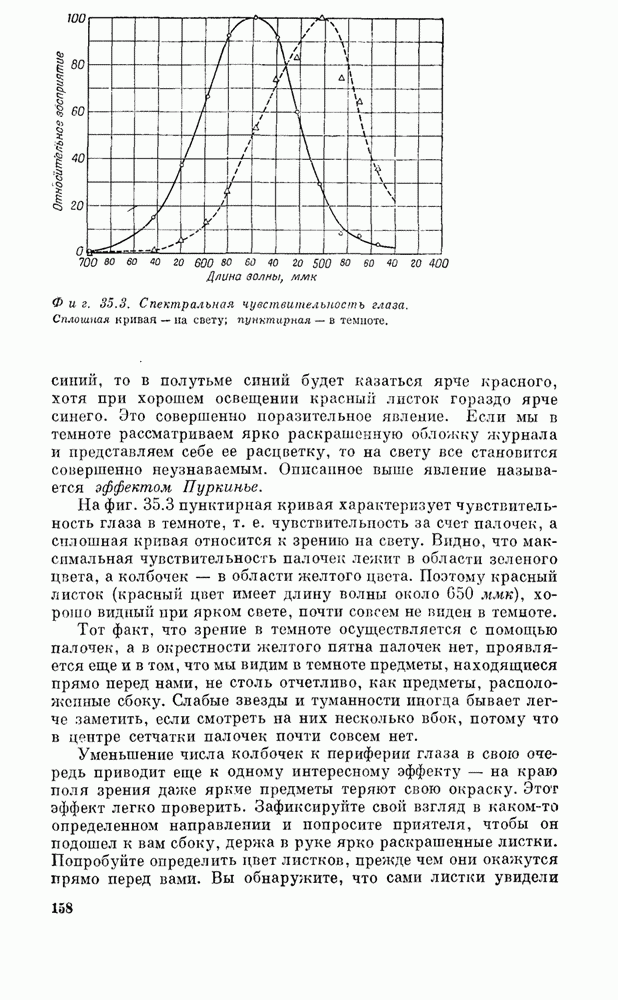
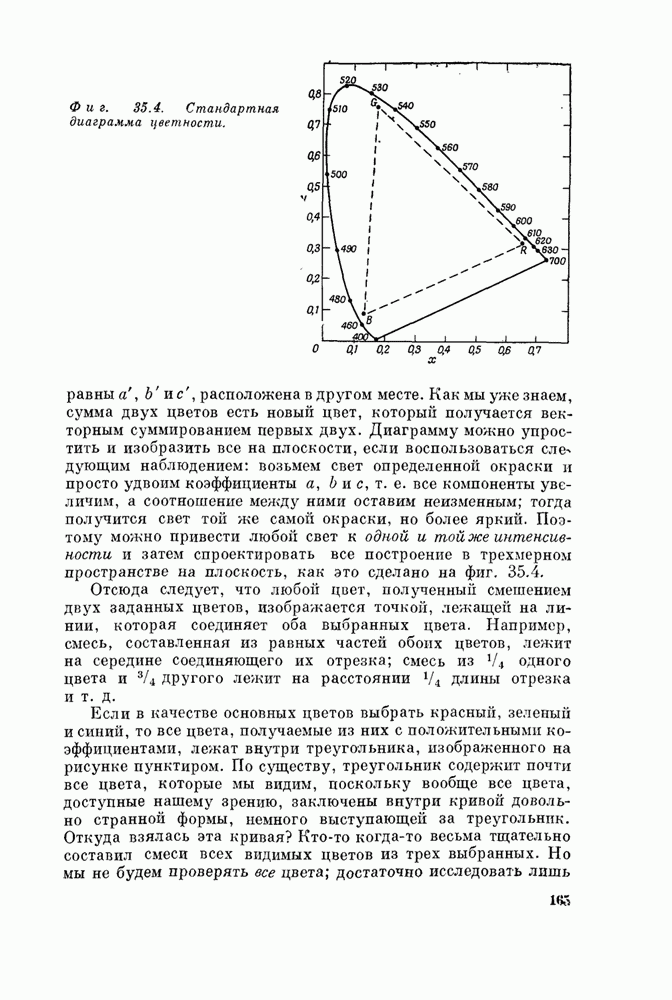
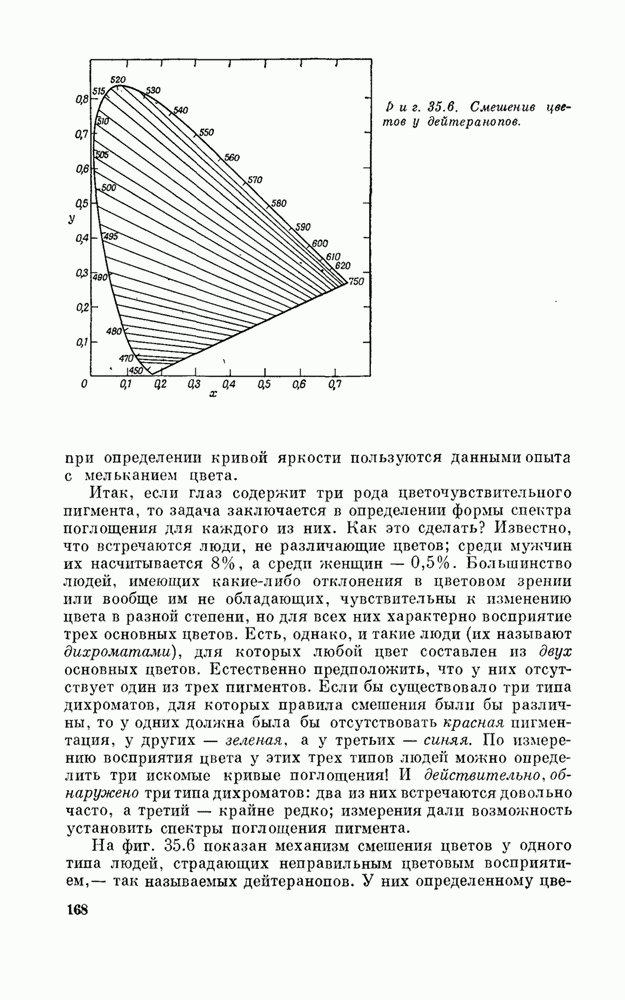
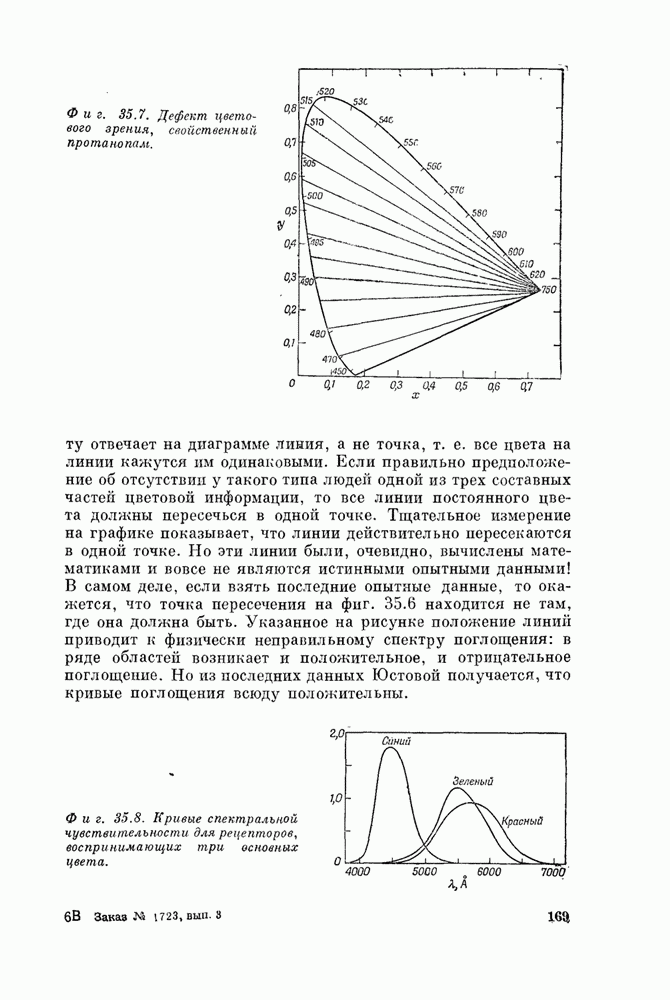
Сам факт зависимости показателя преломления от частоты называется дисперсией, так как именно из-за дисперсии свет «диспергирует», раскладывается призмой в спектр. Формула, выражающая показатель преломления как функцию частоты, называется формулой дисперсии. Итак, мы нашли дисперсионную формулу, (За последние несколько лет «дисперсионные формулы» стали использоваться в теории элементарных частиц.)

Наша дисперсионная формула предсказывает ряд новых интересных эффектов. Если частота  лежит в области видимого света или если измерять показатель преломления вещества, например стекла, для ультрафиолетовых лучей (где  близко к ), то знаменатель стремится к нулю, а показатель преломления становится очень большим. Пусть, далее,  больше . Такой случай возникает, например, если облучать вещества типа стекла рентгеновскими лучами. Кроме того, многие вещества, непрозрачные для обычного света (скажем, уголь), прозрачны для рентгеновских лучей, поэтому можно говорить о показателе преломления этих веществ для рентгеновских лучей. Собственные частоты атомов углерода гораздо меньше частоты рентгеновских лучей. Показатель преломления в этом случае дается нашей дисперсионной формулой, если положить  (т. е. мы пренебрегаем  по сравнению с ).

Аналогичный результат получается при облучении газа свободных электронов радиоволнами (или светом). В верхних слоях атмосферы ультрафиолетовое излучение Солнца выбивает электроны из атомов, в результате чего образуется газ свободных электронов. Для свободных электронов  (упругой возвращающей силы нет). Полагая в нашей дисперсионной формуле , получаем разумную формулу для показателя преломлении радиоволн в стратосфере, где  теперь означает плотность свободных электронов (число на единицу объема) в стратосфере. Но, как видно из формулы, при облучении вещества рентгеновскими лучами или электронного газа радиоволнами член  становится отрицательным, откуда следует, что  меньше единицы. Это значит, что эффективная скорость электромагнитных волн в веществе больше ! Может ли так быть?

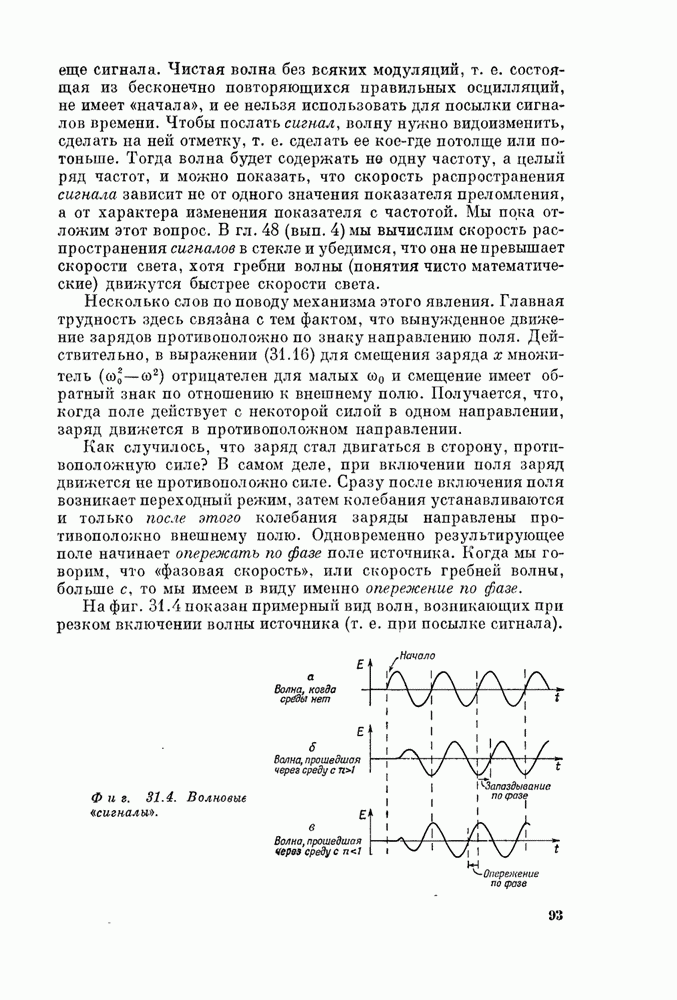
Может. Хотя мы и говорили, что сигналы не могут распространяться быстрее скорости света, тем не менее показатель преломления при некоторой частоте может быть как больше, так и меньше единицы. Это просто означает, что сдвиг фазы за счет рассеяния света либо положителен, либо отрицателен. Кроме того, можно показать, что скорость сигнала определяется показателем преломления не при одном значении частоты, а при многих частотах. Показатель преломления указывает на скорость движения гребня волны. По гребень волны не составляет еще сигнала. Чистая волна без всяких модуляций, т. е. состоящая из бесконечно повторяющихся правильных осцилляции, не имеет «начала», и ее нельзя использовать для посылки сигналов времени. Чтобы послать сигнал, волну нужно видоизменить, сделать на ней отметку, т. е. сделать ее кое-где потолще или потоньше. Тогда волна будет содержать по одну частоту, а целый ряд частот, и можно показать, что скорость распространения сигнала зависит не от одного значения показателя преломления, а от характера изменения показателя с частотой. Мы пока отложим этот вопрос. В гл. 48 (вып. 4) мы вычислим скорость распространения сигналов в стекле и убедимся, что она не превышает скорости света, хотя гребни волны (понятия чисто математические) движутся быстрее скорости света.

Несколько слов по поводу механизма этого явления. Главная трудность здесь связана с тем фактом, что вынужденное движение зарядов противоположно по знаку направлению поля. Действительно, в выражении (31.16) для смещения заряда  множитель  отрицателен для малых  и смещение имеет обратный знак по отношению к внешнему полю. Получается, что, когда поле действует с некоторой силой в одном направлении, заряд движется в противоположном направлении.

Как случилось, что заряд стал двигаться в сторону, противоположную силе? В самом деле, при включении поля заряд движется не противоположно силе. Сразу после включения поля возникает переходный режим, затем колебания устанавливаются и только после этого колебания заряды направлены противоположно внешнему полю. Одновременно результирующее поле начинает опережать по фазе доле источника. Когда мы говорим, что «фазовая скорость», или скорость гребней волны, больше с, то мы имеем в виду именно опережение по фазе.

На фиг. 31.4 показан примерный вид волн, возникающих при резком включении волны источника (т. е. при посылке сигнала).

Фигура 31.4. Волновые «сигналы».

Из рисунка видно, что для волны, проходящей в среде с опережением по фазе, сигнал (т. е. начало волны) не опережает по времени сигнал источника.

Обратимся теперь снова к дисперсионной формуле. Следует помнить, что полученный нами результат несколько упрощает истинную картину явления. Чтобы быть точными, в формулу необходимо внести некоторые поправки. Прежде всего в нашу модель атомного осциллятора следует ввести затухание (иначе осциллятор, раз начав, будет колебаться до бесконечности, что неправдоподобно). Движение затухающего осциллятора мы уже изучали в одной из прошлых глав [см. уравнение (23.8)]. Учет затухания приводит к тому, что в формулах (31.16), а поэтому и в (31.19), вместо  появляется , где  — коэффициент затухания.

Вторая поправка к нашей формуле возникает потому, что каждый атом обычно имеет несколько резонансных частот. Тогда вместо одного вида осцилляторов нужно учесть действие нескольких осцилляторов с разными резонансными частотами, колебания которых происходят независимо друг от друга, и сложить вклады от всех осцилляторов.

Пусть в единице объема содержится  электронов с собственной частотой  и коэффициентом затухания . Наша дисперсионная формула примет в результате вид

                                 (31.20)

Это окончательное выражение для показателя преломления справедливо для большого числа веществ. Примерный ход показателя преломления с частотой, даваемый формулой (31.20), приведен на фиг. 31.5.

Фигура 31.5. Показатель преломления как функция частоты.

Вы видите, что всюду, за исключением области, где  очень близко к одной из резонансных частот, наклон кривой положителен. Такая зависимость носит название «нормальной» дисперсии (потому что этот случай встречается наиболее часто). Вблизи резонансных частот кривая имеет отрицательный наклон, и в этом случае говорят об «аномальной» дисперсии (имея в виду «ненормальную» дисперсию), потому что она была наблюдена задолго до того, как узнали об электронах, и казалась в то время необычной. С нашей точки зрения, оба наклона вполне «нормальны»!