| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Симметрия и ее сохранение
Прежде
чем применять только что найденный результат, хотелось бы еще немного вникнуть
в идею симметрии. Положим, что стечение обстоятельств таково, что после
действия оператора ![]() на состояние получается опять то же
состояние. Это очень частный случай, но все же допустим, что так сложилось, что
состояние
на состояние получается опять то же
состояние. Это очень частный случай, но все же допустим, что так сложилось, что
состояние ![]() физически
совпадает с состоянием
физически
совпадает с состоянием ![]() . Это значит, что
. Это значит, что ![]() равняется
равняется ![]() , если не считать
некоторого фазового множителя. Как это себе представлять? Пусть, например,
имеется ион
, если не считать
некоторого фазового множителя. Как это себе представлять? Пусть, например,
имеется ион ![]() в
состоянии, которое мы когда-то обозначали
в
состоянии, которое мы когда-то обозначали ![]() . У этого состояния имеется
одинаковая амплитуда побывать в базисных состояниях
. У этого состояния имеется
одинаковая амплитуда побывать в базисных состояниях ![]() и
и ![]() . Вероятности показаны
столбиками на фиг. 15.3,а. Если мы на состояние
. Вероятности показаны
столбиками на фиг. 15.3,а. Если мы на состояние ![]() подействуем оператором отражения
подействуем оператором отражения ![]() , он перевернет
его, поменяв местами
, он перевернет
его, поменяв местами ![]() с
с ![]() ,
, ![]() с
с ![]() ; получатся вероятности, показанные
на фиг. 15.3,б. Перед нами опять состояние
; получатся вероятности, показанные
на фиг. 15.3,б. Перед нами опять состояние ![]() . Если начать с состояния
. Если начать с состояния ![]() , то вероятности
до и после отражения будут выглядеть тоже одинаково. Правда, если посмотреть на
амплитуды, то разница все же есть. У состояния
, то вероятности
до и после отражения будут выглядеть тоже одинаково. Правда, если посмотреть на
амплитуды, то разница все же есть. У состояния ![]() после отражения амплитуды останутся
теми же, у состояния
после отражения амплитуды останутся
теми же, у состояния ![]() они приобретут противоположный знак.
Иными словами,
они приобретут противоположный знак.
Иными словами,
 (15.12)
(15.12)
Если
написать ![]() ,
то у состояния
,
то у состояния ![]() мы
имеем
мы
имеем ![]() ,
а у состояния
,
а у состояния ![]() имеем
имеем
![]() .
.

Фиг. 15.3. Состояние ![]() и состояние
и состояние ![]() , получаемые
отражением
, получаемые
отражением ![]() в
плоскости, проходящей посредине между атомами в ионе
в
плоскости, проходящей посредине между атомами в ионе ![]() .
.
Возьмем
другой пример. Пусть у нас есть правополяризованный по кругу фотон,
распространяющийся в направлении ![]() . Если мы совершим операцию поворота
вокруг оси
. Если мы совершим операцию поворота
вокруг оси ![]() ,
то, как мы знаем, это просто приведет к умножению амплитуды на
,
то, как мы знаем, это просто приведет к умножению амплитуды на ![]() , где
, где ![]() - угол поворота.
Значит, в этом случае для операции поворота
- угол поворота.
Значит, в этом случае для операции поворота ![]() просто равно углу поворота.
просто равно углу поворота.
Далее,
ясно, что если оказывается верным, что оператор ![]() в какой-то момент времени просто
меняет фазу состояния (скажем, в момент
в какой-то момент времени просто
меняет фазу состояния (скажем, в момент ![]() ), то это будет верно всегда. Иначе
говоря, если состояние
), то это будет верно всегда. Иначе
говоря, если состояние ![]() переходит за время
переходит за время ![]() в состояние
в состояние ![]() :
:
![]() , (15.13)
, (15.13)
и если симметрия физической картины такова, что
![]() , (15.14)
, (15.14)
то верно и то, что
![]() . (15.15)
. (15.15)
Это ясно, ведь
![]() ,
,
и
если ![]() ,
то
,
то
![]() .
.
[Верхние
равенства следуют из (15.13) и (15.10) для симметричной системы, нижние - из
(15.14) и из того, что всякое число, скажем ![]() , коммутирует с оператором.]
, коммутирует с оператором.]
Итак, при некоторых симметриях то, что верно сначала, верно всегда. Но разве это не закон сохранения? Да! Он утверждает, что если вы взглянете на исходное состояние и, проделав где-то в стороне небольшой подсчет, откроете, что операция, которая является операцией симметрии для системы, приводит только к умножению на некоторый фазовый множитель, то вы будете уверены, что это же свойство будет выполнено для конечного состояния - та же операция умножит и конечное состояние на тот же фазовый множитель. Это будет верно всегда, даже если вы ничего не знаете о том внутреннем механизме мира, который изменяет систему от начального состояния к конечному. Даже если вы не позаботились вглядеться в детали того, каким именно способом система переходит от одного состояния к другому, вы все равно имеете право говорить, что если вещь вначале находилась в состоянии с определенным характером симметрии и если гамильтониан этой вещи симметричен относительно этой операции симметрии, тогда тот же характер симметрии останется у состояния на вечные времена. Это основа всех законов сохранения квантовой механики.
Рассмотрим
частный пример. Возьмем опять оператор ![]() . Сперва, правда, немножко изменим
определение операции
. Сперва, правда, немножко изменим
определение операции ![]() . Пусть
. Пусть ![]() будет не просто зеркальным
отражением, потому что оно требует определения плоскости, в которой поставлено
зеркало. Существует особый вид отражения, который указания плоскости не
требует. Переопределим операцию
будет не просто зеркальным
отражением, потому что оно требует определения плоскости, в которой поставлено
зеркало. Существует особый вид отражения, который указания плоскости не
требует. Переопределим операцию ![]() таким образом: сперва вы отражаете в
зеркале, находящемся в плоскости
таким образом: сперва вы отражаете в
зеркале, находящемся в плоскости ![]() , так что
, так что ![]() переходит в
переходит в ![]() ,
, ![]() остается
остается ![]() , а
, а ![]() остается
остается ![]() ; затем вы
поворачиваете систему на угол 180° вокруг оси
; затем вы
поворачиваете систему на угол 180° вокруг оси ![]() , так что
, так что ![]() переходит в
переходит в ![]() , а
, а ![]() в
в ![]() . Все вместе
называется инверсией, обращением координат. Каждая точка проецируется через
начало координат в диаметрально противоположное положение. Все координаты всего
на свете меняют знак. Эту операцию мы, как и прежде, будем обозначать символом
. Все вместе
называется инверсией, обращением координат. Каждая точка проецируется через
начало координат в диаметрально противоположное положение. Все координаты всего
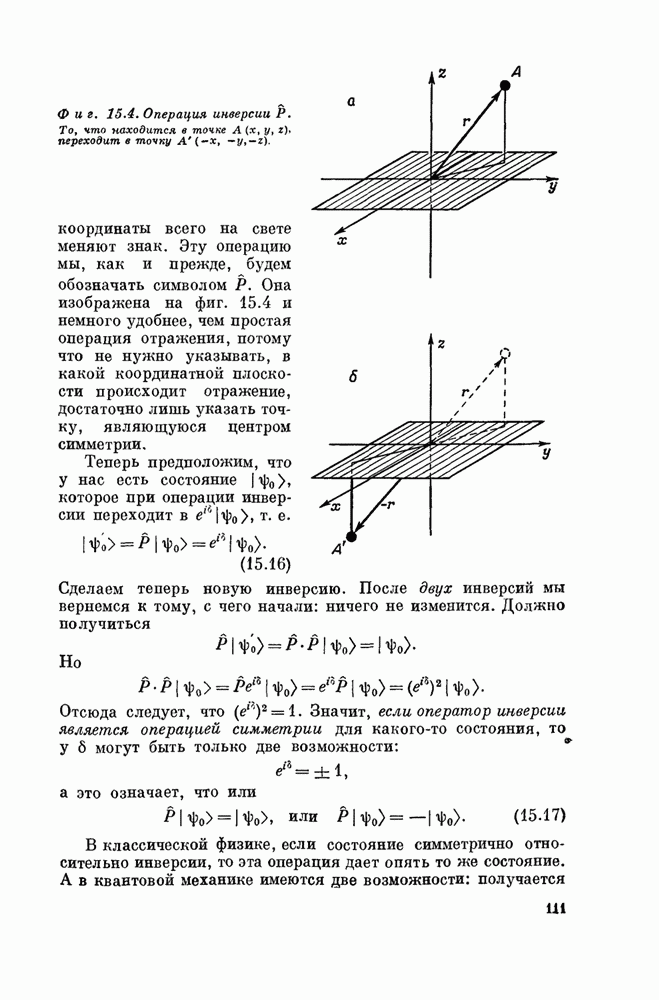
на свете меняют знак. Эту операцию мы, как и прежде, будем обозначать символом ![]() . Она изображена
на фиг. 15.4 и немного удобнее, чем простая операция отражения, потому что не
нужно указывать, в какой координатной плоскости происходит отражение,
достаточно лишь указать точку, являющуюся центром симметрии.
. Она изображена
на фиг. 15.4 и немного удобнее, чем простая операция отражения, потому что не
нужно указывать, в какой координатной плоскости происходит отражение,
достаточно лишь указать точку, являющуюся центром симметрии.

Фиг. 15.4. Операция инверсии ![]() .
.
То, что находится в точке ![]() , переходит в
точку
, переходит в
точку ![]() .
.
Теперь
предположим, что у нас есть состояние ![]() , которое при операции инверсии
переходит в
, которое при операции инверсии
переходит в ![]() ,
т. е.
,
т. е.
![]() . (15.16)
. (15.16)
Сделаем теперь новую инверсию. После двух инверсий мы вернемся к тому, с чего начали: ничего не изменится. Должно получиться
![]() .
.
Но
![]() .
.
Отсюда
следует, что ![]() .
Значит, если оператор инверсии является операцией симметрии для какого-то
состояния, то у
.
Значит, если оператор инверсии является операцией симметрии для какого-то
состояния, то у ![]() могут
быть только две возможности:
могут
быть только две возможности:
![]() ,
,
а это означает, что или
![]() ,
или
,
или ![]() . (15.17)
. (15.17)
В
классической физике, если состояние симметрично относительно инверсии, то эта
операция дает опять то же состояние. А в квантовой механике имеются две
возможности: получается либо тоже состояние, либо минус тоже состояние. Когда
получается то же состояние, ![]() , мы говорим, что у состояния
, мы говорим, что у состояния ![]() четность
положительна. Если знак меняется, так что
четность
положительна. Если знак меняется, так что ![]() , мы говорим, что четность состояния
отрицательна. (Оператор инверсии
, мы говорим, что четность состояния
отрицательна. (Оператор инверсии ![]() известен также как оператор
четности.) Состояние
известен также как оператор
четности.) Состояние ![]() иона
иона ![]() обладает положительной четностью;
состояние же
обладает положительной четностью;
состояние же ![]() -
отрицательной [см. (15.12)]. Бывают, конечно, состояния, не симметричные
относительно операции
-
отрицательной [см. (15.12)]. Бывают, конечно, состояния, не симметричные
относительно операции ![]() ; это состояния без определенной
четности. Например, в системе
; это состояния без определенной
четности. Например, в системе ![]() состояние
состояние ![]() имеет положительную
четность, состояние
имеет положительную
четность, состояние ![]() - отрицательную, а состояние
- отрицательную, а состояние ![]() определенной
четности не имеет.
определенной
четности не имеет.
Когда
мы говорим о том, что операция (например, инверсия) была совершена «над
физической системой», то это можно представлять себе двояким образом. Можно
считать, что все, что было в точке ![]() , физически сдвинулось в обратную
точку
, физически сдвинулось в обратную
точку ![]() ;
или можно считать, что мы смотрим на ту же систему из новой системы отсчета
;
или можно считать, что мы смотрим на ту же систему из новой системы отсчета ![]() ,
, ![]() ,
, ![]() , связанной со
старой формулами
, связанной со
старой формулами ![]() ,
, ![]() и
и ![]() . Точно так же, когда мы говорим о
поворотах, то можно либо считать, что мы поворачиваем целиком всю физическую
систему, либо что поворачиваем систему координат, в которой мы измеряем нашу
систему, оставляя последнюю закрепленной в пространстве. Эти две точки зрения
по существу равноценны. Они равноценны и при повороте, только поворот системы
на угол
. Точно так же, когда мы говорим о
поворотах, то можно либо считать, что мы поворачиваем целиком всю физическую
систему, либо что поворачиваем систему координат, в которой мы измеряем нашу
систему, оставляя последнюю закрепленной в пространстве. Эти две точки зрения
по существу равноценны. Они равноценны и при повороте, только поворот системы
на угол ![]() подобен
повороту системы отсчета на отрицательный угол
подобен
повороту системы отсчета на отрицательный угол ![]() . В нашем курсе мы обычно смотрели,
что получается, когда берется проекция на новую систему осей. То, что при этом
получается, совпадает с тем, что получится, если мы оставим оси прежними и
повернем тело на столько же назад. Когда вы это делаете, не забудьте поменять
знаки углов.
. В нашем курсе мы обычно смотрели,
что получается, когда берется проекция на новую систему осей. То, что при этом
получается, совпадает с тем, что получится, если мы оставим оси прежними и
повернем тело на столько же назад. Когда вы это делаете, не забудьте поменять
знаки углов.
Многие
законы физики (но не все) не меняются при отражении или инверсии координат. Они
симметричны по отношению к инверсии. Законы электродинамики, например, не
изменяются, если мы меняем ![]() на
на ![]() ,
, ![]() на
на ![]() и
и ![]() на
на ![]() во всех уравнениях. То же относится
и к законам тяжести, и к сильным взаимодействиям ядерной физики. Только у
слабых взаимодействий, ответственных за
во всех уравнениях. То же относится
и к законам тяжести, и к сильным взаимодействиям ядерной физики. Только у
слабых взаимодействий, ответственных за ![]() -распад, нет такой симметрии. [Мы
обсуждали это несколько подробнее в гл. 52 (вып. 4).] Но мы сейчас пренебрежем
-распад, нет такой симметрии. [Мы
обсуждали это несколько подробнее в гл. 52 (вып. 4).] Но мы сейчас пренебрежем ![]() -распадом. Тогда в
любой физической системе, на которую, как можно думать,
-распадом. Тогда в
любой физической системе, на которую, как можно думать, ![]() -распад не оказывает
заметного влияния (в качестве примера возьмем испускание света атомом),
гамильтониан
-распад не оказывает
заметного влияния (в качестве примера возьмем испускание света атомом),
гамильтониан ![]() и
оператор
и
оператор ![]() будут
коммутировать. В этих обстоятельствах верно следующее утверждение. Если
четность состояния вначале положительна и вы поинтересуетесь физической
ситуацией через некоторое время, то увидите, что четность останется
положительной. Пусть, например, нам известно, что атом перед тем, как испустить
фотон, находился в состоянии с положительной четностью. Вы рассматриваете всю
эту систему (включая фотон) после испускания; четность опять будет положительна
(и точно так же было бы, если бы вы начали с отрицательной четности). Этот
принцип именуется сохранением четности. Вы теперь понимаете, почему слова
«сохранение четности» и «симметрия относительно отражений» в квантовой механике
тесно переплетены. Хотя до последних лет считалось, что природа всегда
сохраняет четность, теперь известно, что это не так. Выяснилось, что это
неверно, потому что реакция
будут
коммутировать. В этих обстоятельствах верно следующее утверждение. Если
четность состояния вначале положительна и вы поинтересуетесь физической
ситуацией через некоторое время, то увидите, что четность останется
положительной. Пусть, например, нам известно, что атом перед тем, как испустить
фотон, находился в состоянии с положительной четностью. Вы рассматриваете всю
эту систему (включая фотон) после испускания; четность опять будет положительна
(и точно так же было бы, если бы вы начали с отрицательной четности). Этот
принцип именуется сохранением четности. Вы теперь понимаете, почему слова
«сохранение четности» и «симметрия относительно отражений» в квантовой механике
тесно переплетены. Хотя до последних лет считалось, что природа всегда
сохраняет четность, теперь известно, что это не так. Выяснилось, что это
неверно, потому что реакция ![]() -распада не обладает симметрией
относительно инверсии, обнаруженной в других законах физики.
-распада не обладает симметрией
относительно инверсии, обнаруженной в других законах физики.
Теперь мы можем доказать интересную теорему (справедливую до тех пор, пока слабыми взаимодействиями можно пренебрегать): любое состояние определенной энергии, не являющееся вырожденным, обязано обладать определенной четностью. Его четность должна быть либо положительна, либо отрицательна. (Припомните, что нам иногда встречались системы, в которых несколько состояний имели одну и ту же энергию, - такие состояния мы называем вырожденными. Так вот наша теорема к ним не относится.)
Мы
знаем, что если ![]() -
состояние определенной энергии, то
-
состояние определенной энергии, то
![]() , (15.18)
, (15.18)
где
![]() -
просто число, энергия состояния. Если у нас имеется произвольный оператор
-
просто число, энергия состояния. Если у нас имеется произвольный оператор ![]() , который является
оператором симметрии для системы, то мы можем доказать, что
, который является
оператором симметрии для системы, то мы можем доказать, что
![]() , (15.19)
, (15.19)
если
только ![]() -
единственное состояние с данной энергией. Рассмотрим новое состояние
-
единственное состояние с данной энергией. Рассмотрим новое состояние ![]() , которое вы
получаете после действия
, которое вы
получаете после действия ![]() . Если вся физика симметрична, то
. Если вся физика симметрична, то ![]() должно иметь ту
же энергию, что и
должно иметь ту
же энергию, что и ![]() . Но мы ведь выбрали случай, когда
состояние с такой энергией только одно, а именно
. Но мы ведь выбрали случай, когда
состояние с такой энергией только одно, а именно ![]() ; значит,
; значит, ![]() должно быть тем же состоянием,
отличаясь разве что фазой. Таково физическое доказательство.
должно быть тем же состоянием,
отличаясь разве что фазой. Таково физическое доказательство.
Но
то же последует и из нашей математики. Наше определение симметрии - это (15.10)
или (15.11), справедливое для любого состояния ![]() :
:
![]() . (15.20)
. (15.20)
Но
сейчас речь идет о состоянии ![]() , которое является состоянием с
определенной энергией, так что
, которое является состоянием с
определенной энергией, так что ![]() . А раз
. А раз ![]() - просто число, то оно попросту
проходит сквозь
- просто число, то оно попросту
проходит сквозь ![]() ,
и мы имеем
,
и мы имеем
![]() ,
,
так что
![]() . (15.21)
. (15.21)
Значит,
![]() - тоже
состояние
- тоже
состояние ![]() с
определенной энергией и при этом с тем же самым
с
определенной энергией и при этом с тем же самым ![]() . Но по нашей гипотезе имеется только
одно такое состояние; значит,
. Но по нашей гипотезе имеется только
одно такое состояние; значит, ![]() должно быть равно
должно быть равно ![]() .
.
Все,
что мы только что доказали, относится к любому оператору ![]() , лишь бы он был оператором
симметрии для физической системы. Поэтому когда в рассмотрение входят только
электрические силы и сильные взаимодействия (и нет никакого
, лишь бы он был оператором
симметрии для физической системы. Поэтому когда в рассмотрение входят только
электрические силы и сильные взаимодействия (и нет никакого ![]() -распада), так что
симметрия относительно инверсии является вполне допустимым приближением, в этих
обстоятельствах
-распада), так что
симметрия относительно инверсии является вполне допустимым приближением, в этих
обстоятельствах ![]() .
Но мы видели также, что
.
Но мы видели также, что ![]() обязано равняться либо
обязано равняться либо ![]() , либо
, либо ![]() . Итак, любое
состояние с определенной энергией (если оно не вырождено) навсегда снабжено
либо положительной, либо отрицательной четностью.
. Итак, любое
состояние с определенной энергией (если оно не вырождено) навсегда снабжено
либо положительной, либо отрицательной четностью.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 11. РАСПРОСТРАНЕНИЕ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ
- § 1. Состояния электрона в одномерной решетке
- § 2. Состояния определенной энергии
- § 3. Состояния, зависящие от времени
- § 4. Электрон в трехмерной решетке
- § 5. Другие состояния в решетке
- § 6. Рассеяние на нерегулярностях решетки
- § 7. Захват нерегулярностями решетки
- § 8. Амплитуды рассеяния и связанные состояния
- Глава 12. ПОЛУПРОВОДНИКИ
- § 1. Электроны и дырки в полупроводниках
- § 2. Примесные полупроводники
- § 3. Эффект Холла
- § 4. Переходы между полупроводниками
- § 5. Выпрямление на полупроводниковом переходе
- § 6. Транзистор
- Глава 13. ПРИБЛИЖЕНИЕ НЕЗАВИСИМЫХ ЧАСТИЦ
- § 1. Спиновые волны
- § 2. Две спиновые волны
- § 3. Независимые частицы
- § 4. Молекула бензола
- § 5. Еще немного органической химии
- § 6. Другие применения приближения
- Глава 14. ЗАВИСИМОСТЬ АМПЛИТУД ОТ МЕСТА
- § 1. Как меняются амплитуды вдоль прямой
- § 2. Волновая функция
- § 3. Состояния с определенным импульсом
- § 4. Нормировка состояний с определенной координатой x
- § 5. Уравнение Шредингера
- § 6. Квантованные уровни энергии
- Глава 15. СИММЕТРИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Симметрия
- § 2. Симметрия и ее сохранение
- § 3. Законы сохранения
- § 4. Поляризованный свет
- § 5. Распад
- § 6. Сводка матриц поворота
- Глава 16. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. Электрическое дипольное излучение
- § 2. Рассеяние света
- § 3. Аннигиляция позитрония
- § 4. Матрица поворота для произвольного спина
- § 5. Измерение ядерного спина
- § 6. Сложение моментов количества движения
- Глава 17. АТОМ ВОДОРОДА И ПЕРИОДИЧЕСКАЯ ТАБЛИЦА
- § 1. Уравнение Шредингера для атома водорода
- § 2. Сферически симметричные решения
- § 3. Состояния с угловой зависимостью
- § 4. Общее решение для водорода
- § 5. Волновые функции водорода
- § 6. Периодическая таблица
- Глава 18. ОПЕРАТОРЫ
- § 1. Операции и операторы
- § 2. Средние энергии
- § 3. Средняя энергия атома
- § 4. Оператор места
- § 5. Оператор импульса
- § 6. Момент количества движения
- § 7. Изменение средних со временем
- Глава 19. УРАВНЕНИЕ ШРЕДИНГЕРА В КЛАССИЧЕСКОМ КОНТЕКСТЕ. СЕМИНАР ПО СВЕРХПРОВОДИМОСТИ
- § 1. Уравнение Шредингера в магнитном поле
- § 2. Уравнение непрерывности для вероятностей
- § 3. Два рода импульсов
- § 4. Смысл волновой функции
- § 5. Сверхпроводимость
- § 6. Явление Мейсснера
- § 7. Квантование потока
- § 8. Динамика сверхпроводимости
- § 9. Переходы Джозефсона
- Эпилог
- От редактора перевода