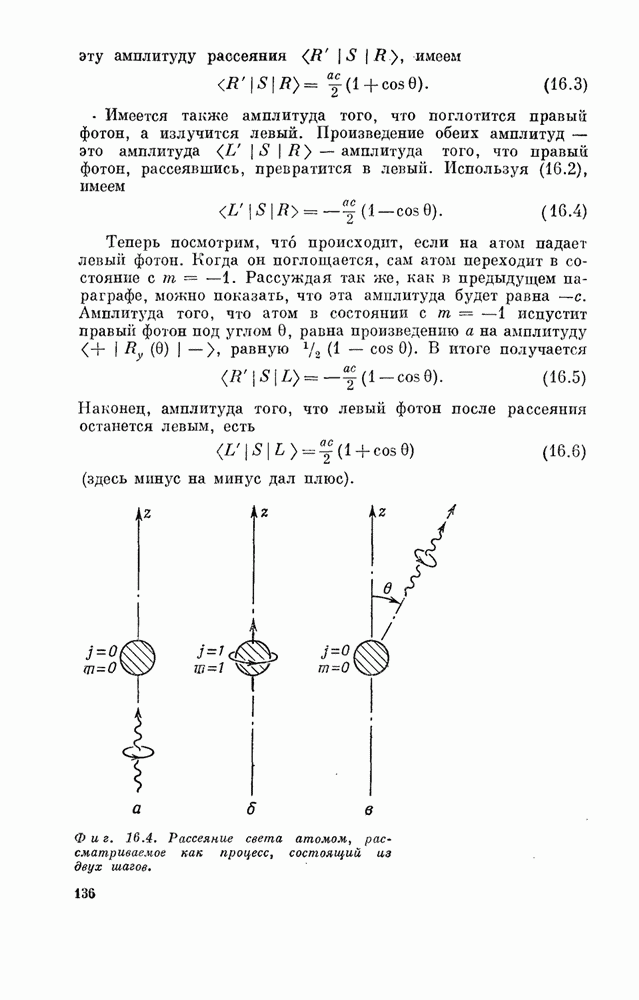
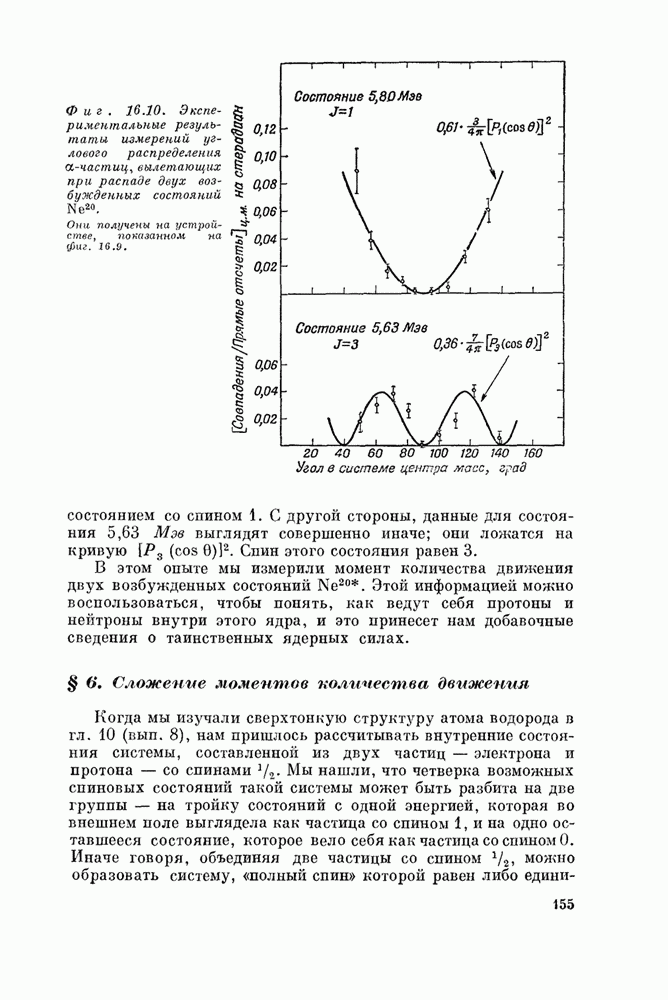
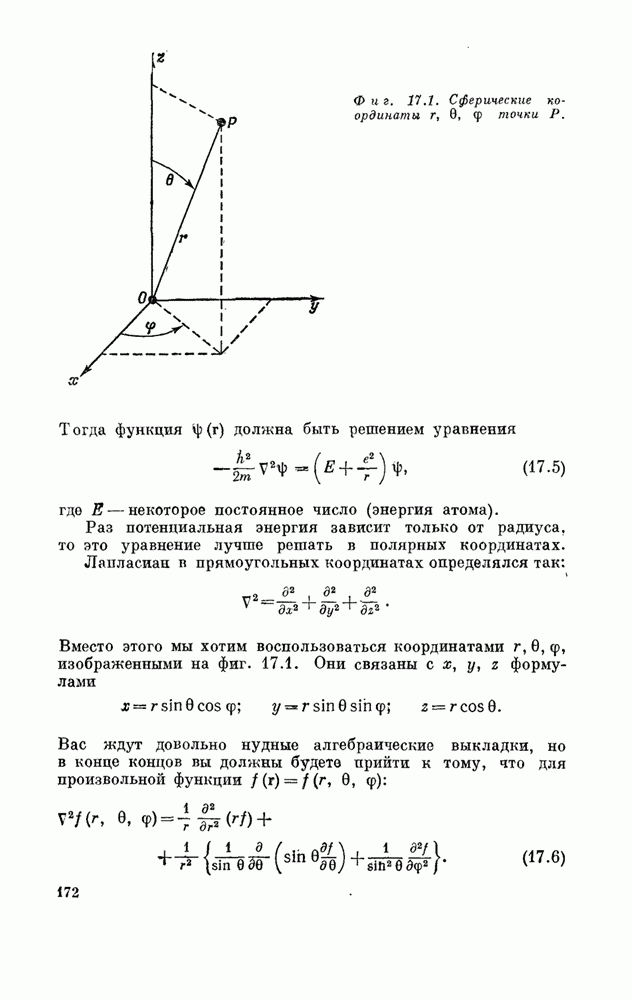
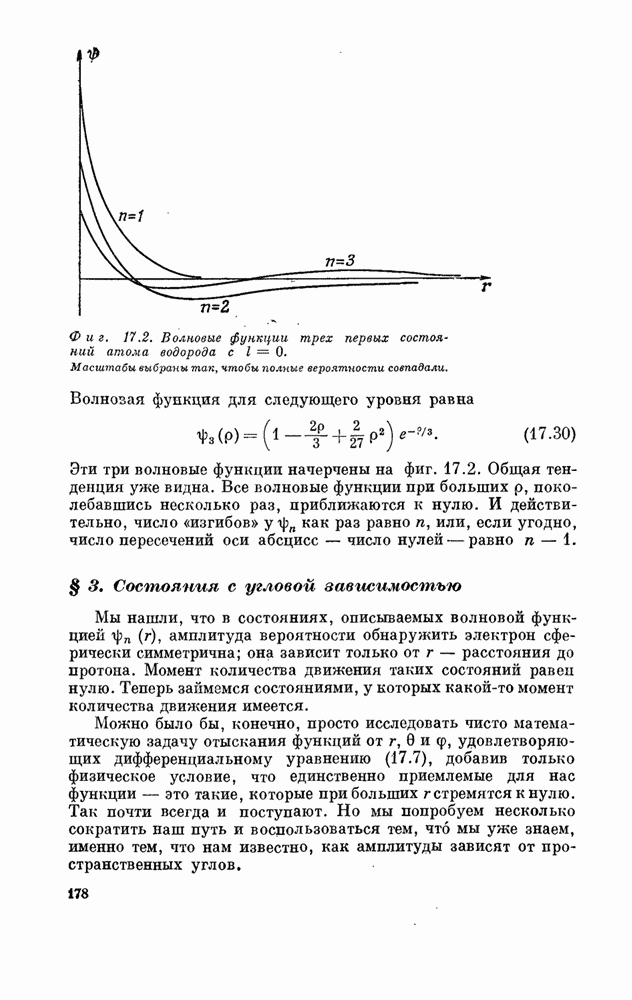
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
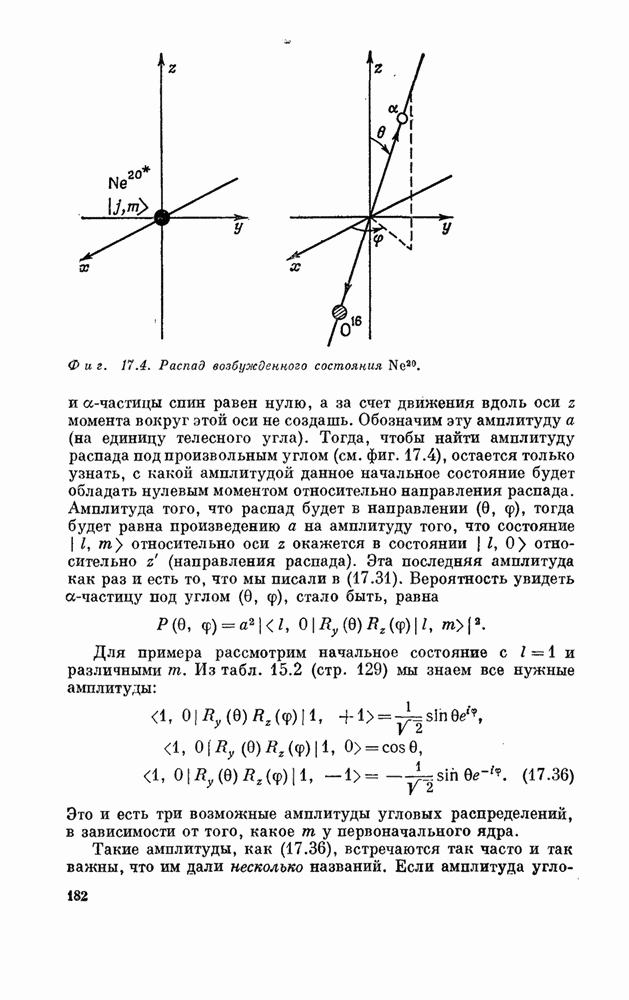
§ 6. Рассеяние на нерегулярностях решетки
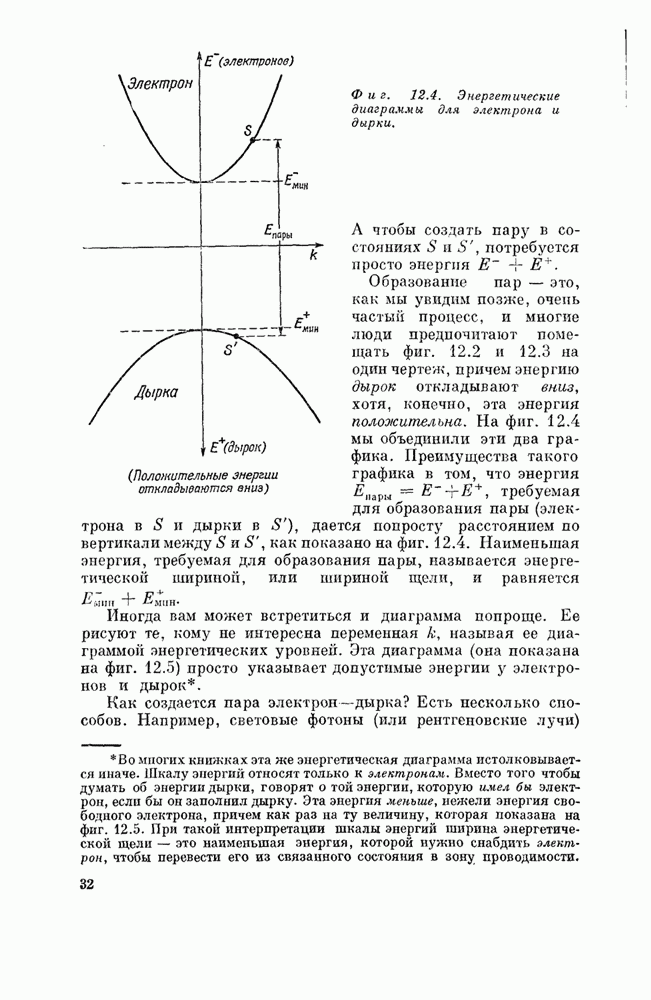
Теперь
мы хотим рассмотреть одиночный электрон в неидеальном кристалле. Наш
первоначальный анализ привел к выводу, что у идеальных кристаллов и
проводимость идеальна, что электроны могут скользить по кристаллу, как по
вакууму, без трения. Одной из самых важных причин, способных прекратить вечное
движение электрона, является несовершенство кристалла, какая-то нерегулярность
в нем. Допустим, что где-то в кристалле не хватает одного атома, или
предположим, что кто-то поставил на место, предназначенное для какого-то атома,
совсем не тот атом, какой положено, так что в этом месте все совсем не так, как
в прочих местах. Скажем, другая энергия ![]() или другая амплитуда
или другая амплитуда ![]() . Как тогда можно
будет описать все происходящее?
. Как тогда можно
будет описать все происходящее?
Для
определенности вернемся к одномерному случаю и допустим, что атом номер «нуль» -
это атом «загрязнения», «примеси» и у него совсем не такая энергия ![]() , как у других
атомов. Обозначим эту энергию
, как у других
атомов. Обозначим эту энергию ![]() . Что же происходит? Для электрона,
который достиг атома «нуль», есть какая-то вероятность того, что он рассеется назад.
Если волновой пакет, мчась по кристаллу, достигает места, где все немного
иначе, то часть его будет продолжать лететь вперед, а другая отскочит назад.
Анализировать такой случай, пользуясь волновым пакетом, очень трудно, потому
что все меняется во времени. С решениями в виде установившихся состояний
работать много легче. Мы обратимся поэтому к стационарным состояниям; мы
увидим, что их можно составить из непрерывных волн, состоящих из двух частей -
пробегающей и отраженной. В случае трех измерений мы бы назвали отраженную
часть рассеянной волной, потому что она разбегалась бы во все стороны.
. Что же происходит? Для электрона,
который достиг атома «нуль», есть какая-то вероятность того, что он рассеется назад.
Если волновой пакет, мчась по кристаллу, достигает места, где все немного
иначе, то часть его будет продолжать лететь вперед, а другая отскочит назад.
Анализировать такой случай, пользуясь волновым пакетом, очень трудно, потому
что все меняется во времени. С решениями в виде установившихся состояний
работать много легче. Мы обратимся поэтому к стационарным состояниям; мы
увидим, что их можно составить из непрерывных волн, состоящих из двух частей -
пробегающей и отраженной. В случае трех измерений мы бы назвали отраженную
часть рассеянной волной, потому что она разбегалась бы во все стороны.
Исходим
из системы уравнений, похожей на (11.6), за одним исключением: уравнение при ![]() не похоже на
остальные. Пятерка уравнений при
не похоже на
остальные. Пятерка уравнений при ![]() и
и ![]() выглядит так:
выглядит так:
 (11.28)
(11.28)
Конечно,
будут и другие уравнения при ![]() . Они будут выглядеть так же, как
(11.6).
. Они будут выглядеть так же, как
(11.6).
Нам
полагалось бы на самом деле для общности писать разные ![]() , в зависимости от того,
прыгает ли электрон к атому «нуль» или же от атома «нуль», но главные черты
того, что происходит, вы увидите уже из упрощенного примера, когда все
, в зависимости от того,
прыгает ли электрон к атому «нуль» или же от атома «нуль», но главные черты
того, что происходит, вы увидите уже из упрощенного примера, когда все ![]() равны.
равны.
Уравнение
(11.10) по-прежнему будет служить решением для всех уравнений, кроме уравнения
для атома «нуль» (для него оно не годится). Нам нужно другое решение; соорудим
его так. Уравнение (11.10) представляет волну, бегущую в положительном
направлении ![]() .
Волна, бегущая в отрицательном направлении
.
Волна, бегущая в отрицательном направлении ![]() , тоже подошла бы в качестве решения.
Мы бы написали
, тоже подошла бы в качестве решения.
Мы бы написали
![]() .
.
Самое общее решение уравнения (11.6) представляло бы собой сочетание волны вперед и волны назад:
![]() . (11.29)
. (11.29)
Это
решение представляет комплексную волну с амплитудой ![]() , бегущую в направлении
, бегущую в направлении ![]() , и волну с
амплитудой
, и волну с
амплитудой ![]() ,
бегущую в направлении
,
бегущую в направлении ![]() .
.
Теперь
бросим взгляд на систему уравнений нашей новой задачи: на (11.28) плюс такие же
уравнения для остальных атомов. Уравнения, куда входят ![]() с
с ![]() , решаются формулой (11.29)
при условии, что
, решаются формулой (11.29)
при условии, что ![]() оказывается
связанным с
оказывается
связанным с ![]() и
постоянной решетки
и
постоянной решетки ![]() соотношением
соотношением
![]() . (11.30)
. (11.30)
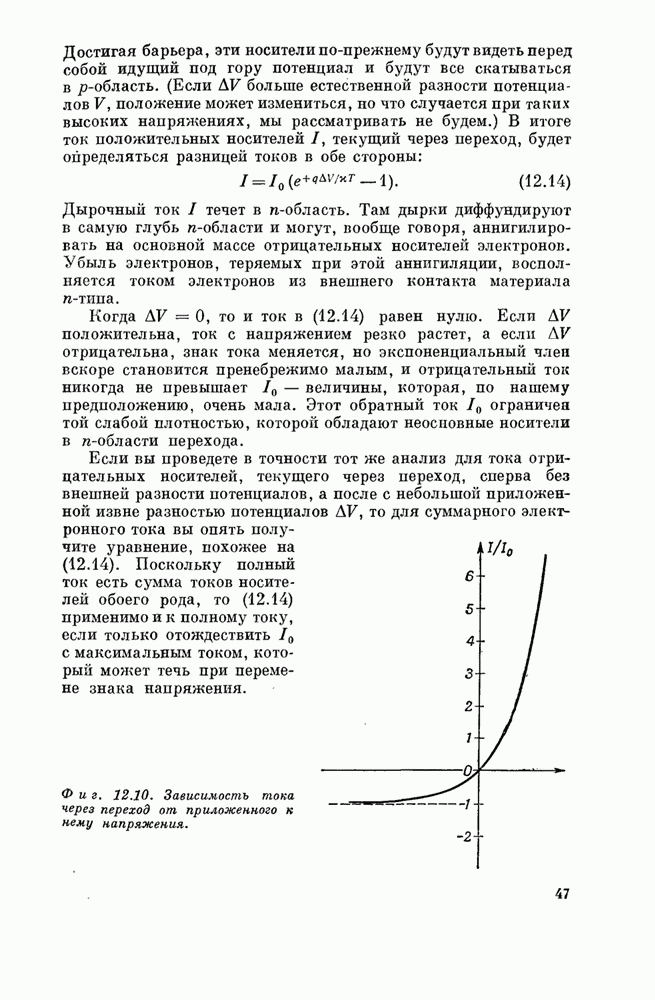
Физический
смысл этого таков: «падающая» волна с амплитудой ![]() приближается к атому «нуль» (или
«рассеивателю») слева, а «рассеянная» или «отраженная» волна с амплитудой
приближается к атому «нуль» (или
«рассеивателю») слева, а «рассеянная» или «отраженная» волна с амплитудой ![]() бежит обратно, т.
е. налево. Не теряя общности, можно положить амплитуду
бежит обратно, т.
е. налево. Не теряя общности, можно положить амплитуду ![]() падающей волны равной
единице. Тогда амплитуда
падающей волны равной
единице. Тогда амплитуда ![]() будет, вообще говоря, комплексным
числом.
будет, вообще говоря, комплексным
числом.
То
же самое можно сказать и о решениях ![]() при
при ![]() . Коэффициенты могут стать иными, так
что следовало бы писать
. Коэффициенты могут стать иными, так
что следовало бы писать
![]() для
для
![]() . (11.31)
. (11.31)
Здесь
![]() -
амплитуда волны, бегущей направо, а
-
амплитуда волны, бегущей направо, а ![]() - амплитуда волны, приходящей справа.
Мы хотим рассмотреть такой физический случай, когда вначале волна бежит только
слева, и за рассеивателем (или атомом загрязнения) имеется только «прошедшая»
волна. Будем поэтому искать решение, в котором
- амплитуда волны, приходящей справа.
Мы хотим рассмотреть такой физический случай, когда вначале волна бежит только
слева, и за рассеивателем (или атомом загрязнения) имеется только «прошедшая»
волна. Будем поэтому искать решение, в котором ![]() . Стало быть, мы попытаемся
удовлетворить всем уравнениям для
. Стало быть, мы попытаемся
удовлетворить всем уравнениям для ![]() , кроме средней тройки в (11.28), с
помощью следующих пробных решений:
, кроме средней тройки в (11.28), с
помощью следующих пробных решений:
 (11.32)
(11.32)
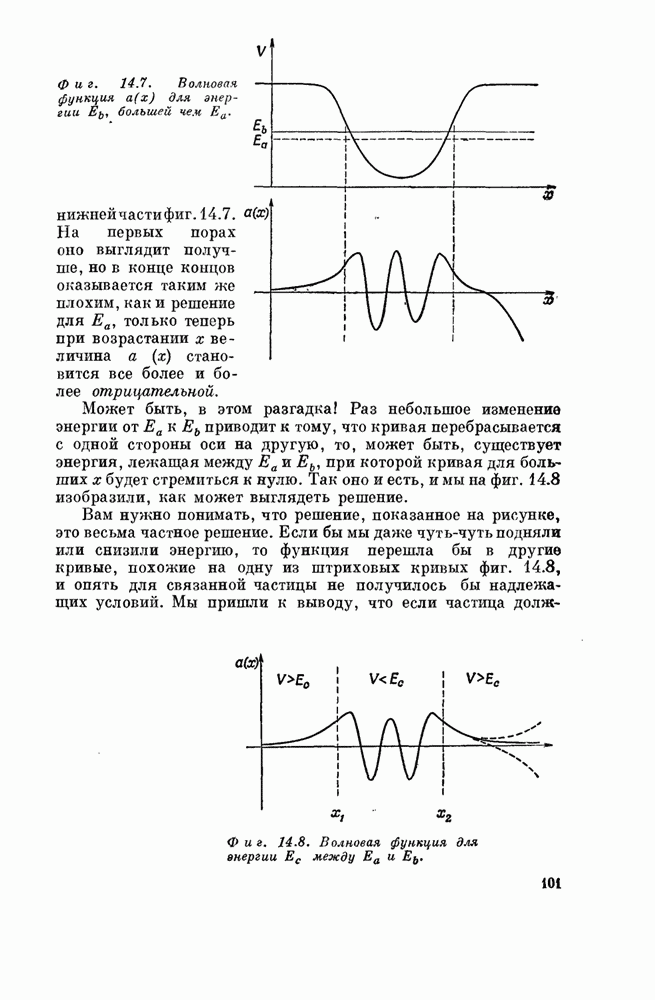
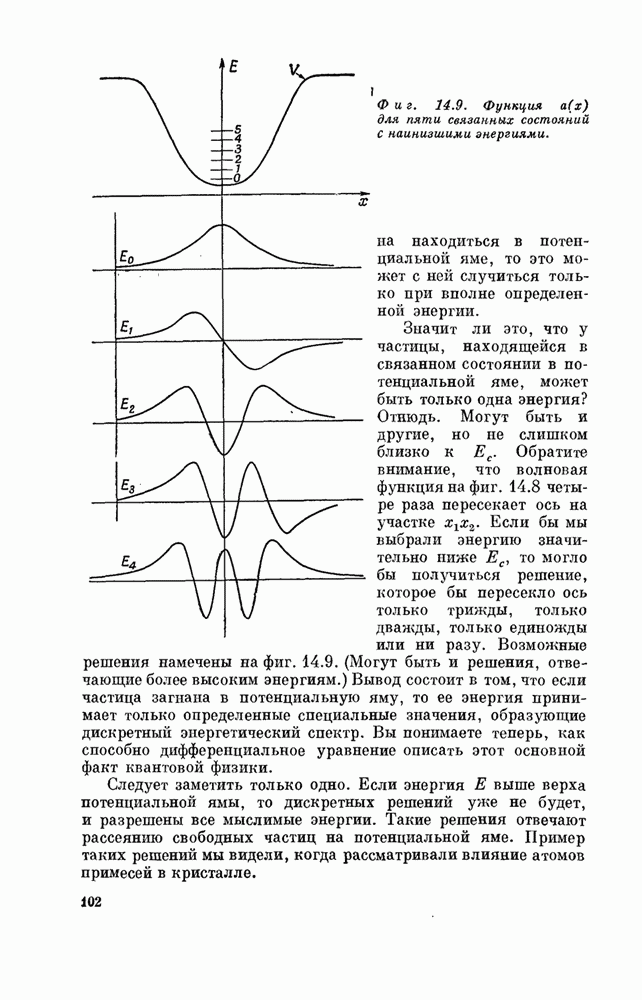
Положение, о котором идет речь, иллюстрируется фиг. 11.6.

Фиг. 11.6. Волны в одномерной
решетке с одним, «примесным» атомом в ![]() .
.
Используя
формулы (11.32) для ![]() и
и ![]() , можно из средней тройки уравнений
(11.28) найти
, можно из средней тройки уравнений
(11.28) найти ![]() и
два коэффициента
и
два коэффициента ![]() и
и
![]() . Таким
образом, мы найдем полное решение. Надо решить три уравнения (полагая
. Таким
образом, мы найдем полное решение. Надо решить три уравнения (полагая ![]() ):
):
 (11.33)
(11.33)
Вспомните,
что (11.30) выражает ![]() через
через ![]() . Подставьте это значение
. Подставьте это значение ![]() в уравнения и
учтите, что
в уравнения и
учтите, что
![]() ;
;
тогда из первого уравнения получится
![]() , (11.34)
, (11.34)
а из третьего
![]() , (11.35)
, (11.35)
что согласуется друг с другом только тогда, когда
![]() . (11.36)
. (11.36)
Это
уравнение сообщает нам, что прошедшая волна ![]() - это просто исходная падающая волна
(1) плюс добавочная волна
- это просто исходная падающая волна
(1) плюс добавочная волна ![]() , равная отраженной. Это не всегда
так, но при рассеянии на одном только атоме оказывается, что это так. Если бы у
вас была целая группа атомов примеси, то величина, добавляемая к волне, бегущей
вперед, не обязательно вышла бы такой же, как у отраженной волны.
, равная отраженной. Это не всегда
так, но при рассеянии на одном только атоме оказывается, что это так. Если бы у
вас была целая группа атомов примеси, то величина, добавляемая к волне, бегущей
вперед, не обязательно вышла бы такой же, как у отраженной волны.
Амплитуду
![]() отраженной
волны мы можем получить из среднего из уравнений (11.33); окажется, что
отраженной
волны мы можем получить из среднего из уравнений (11.33); окажется, что
![]() . (11.37)
. (11.37)
Мы получили полное решение для решетки с одним необычным атомом.
Вас
могло удивить, отчего это проходящая волна оказалась «выше», чем падавшая, если
судить по уравнению (11.34). Но вспомните, что ![]() и
и ![]() - числа комплексные и что число
частиц в волне (или, лучше сказать, вероятность обнаружить частицу)
пропорционально квадрату модуля амплитуды. В действительности «сохранение числа
электронов» будет выполнено лишь при условии
- числа комплексные и что число
частиц в волне (или, лучше сказать, вероятность обнаружить частицу)
пропорционально квадрату модуля амплитуды. В действительности «сохранение числа
электронов» будет выполнено лишь при условии
![]() . (11.38)
. (11.38)
Попробуйте показать, что в нашем решении так оно и есть.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 11. РАСПРОСТРАНЕНИЕ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ
- § 1. Состояния электрона в одномерной решетке
- § 2. Состояния определенной энергии
- § 3. Состояния, зависящие от времени
- § 4. Электрон в трехмерной решетке
- § 5. Другие состояния в решетке
- § 6. Рассеяние на нерегулярностях решетки
- § 7. Захват нерегулярностями решетки
- § 8. Амплитуды рассеяния и связанные состояния
- Глава 12. ПОЛУПРОВОДНИКИ
- § 1. Электроны и дырки в полупроводниках
- § 2. Примесные полупроводники
- § 3. Эффект Холла
- § 4. Переходы между полупроводниками
- § 5. Выпрямление на полупроводниковом переходе
- § 6. Транзистор
- Глава 13. ПРИБЛИЖЕНИЕ НЕЗАВИСИМЫХ ЧАСТИЦ
- § 1. Спиновые волны
- § 2. Две спиновые волны
- § 3. Независимые частицы
- § 4. Молекула бензола
- § 5. Еще немного органической химии
- § 6. Другие применения приближения
- Глава 14. ЗАВИСИМОСТЬ АМПЛИТУД ОТ МЕСТА
- § 1. Как меняются амплитуды вдоль прямой
- § 2. Волновая функция
- § 3. Состояния с определенным импульсом
- § 4. Нормировка состояний с определенной координатой x
- § 5. Уравнение Шредингера
- § 6. Квантованные уровни энергии
- Глава 15. СИММЕТРИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Симметрия
- § 2. Симметрия и ее сохранение
- § 3. Законы сохранения
- § 4. Поляризованный свет
- § 5. Распад
- § 6. Сводка матриц поворота
- Глава 16. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. Электрическое дипольное излучение
- § 2. Рассеяние света
- § 3. Аннигиляция позитрония
- § 4. Матрица поворота для произвольного спина
- § 5. Измерение ядерного спина
- § 6. Сложение моментов количества движения
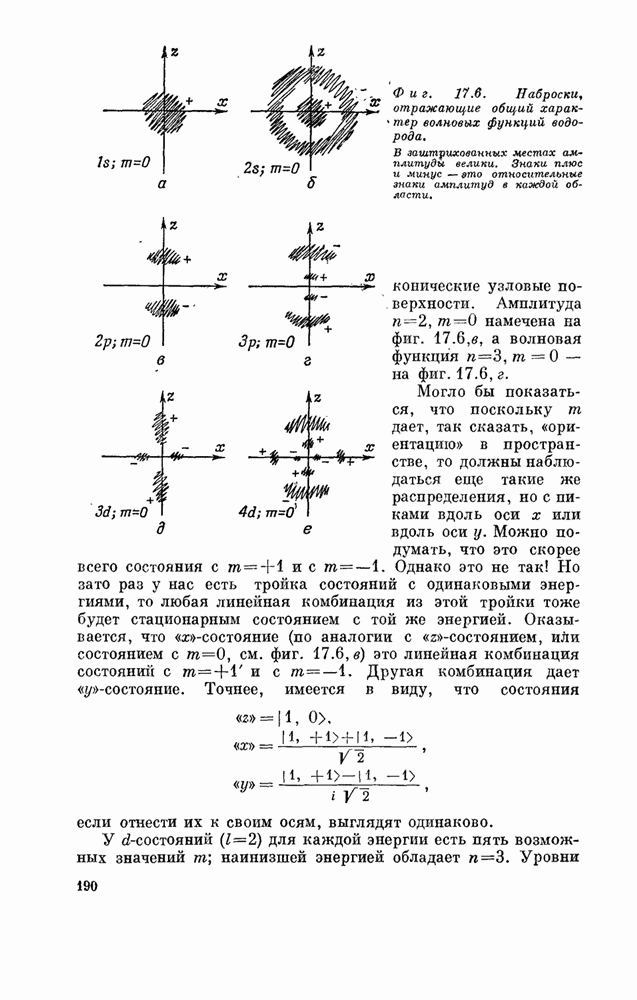
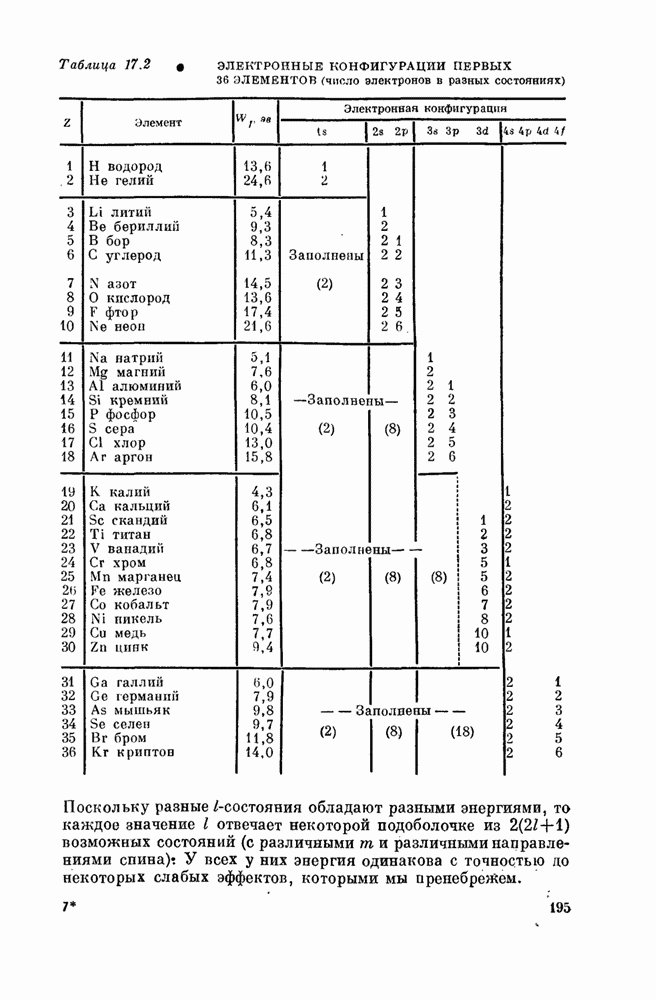
- Глава 17. АТОМ ВОДОРОДА И ПЕРИОДИЧЕСКАЯ ТАБЛИЦА
- § 1. Уравнение Шредингера для атома водорода
- § 2. Сферически симметричные решения
- § 3. Состояния с угловой зависимостью
- § 4. Общее решение для водорода
- § 5. Волновые функции водорода
- § 6. Периодическая таблица
- Глава 18. ОПЕРАТОРЫ
- § 1. Операции и операторы
- § 2. Средние энергии
- § 3. Средняя энергия атома
- § 4. Оператор места
- § 5. Оператор импульса
- § 6. Момент количества движения
- § 7. Изменение средних со временем
- Глава 19. УРАВНЕНИЕ ШРЕДИНГЕРА В КЛАССИЧЕСКОМ КОНТЕКСТЕ. СЕМИНАР ПО СВЕРХПРОВОДИМОСТИ
- § 1. Уравнение Шредингера в магнитном поле
- § 2. Уравнение непрерывности для вероятностей
- § 3. Два рода импульсов
- § 4. Смысл волновой функции
- § 5. Сверхпроводимость
- § 6. Явление Мейсснера
- § 7. Квантование потока
- § 8. Динамика сверхпроводимости
- § 9. Переходы Джозефсона
- Эпилог
- От редактора перевода