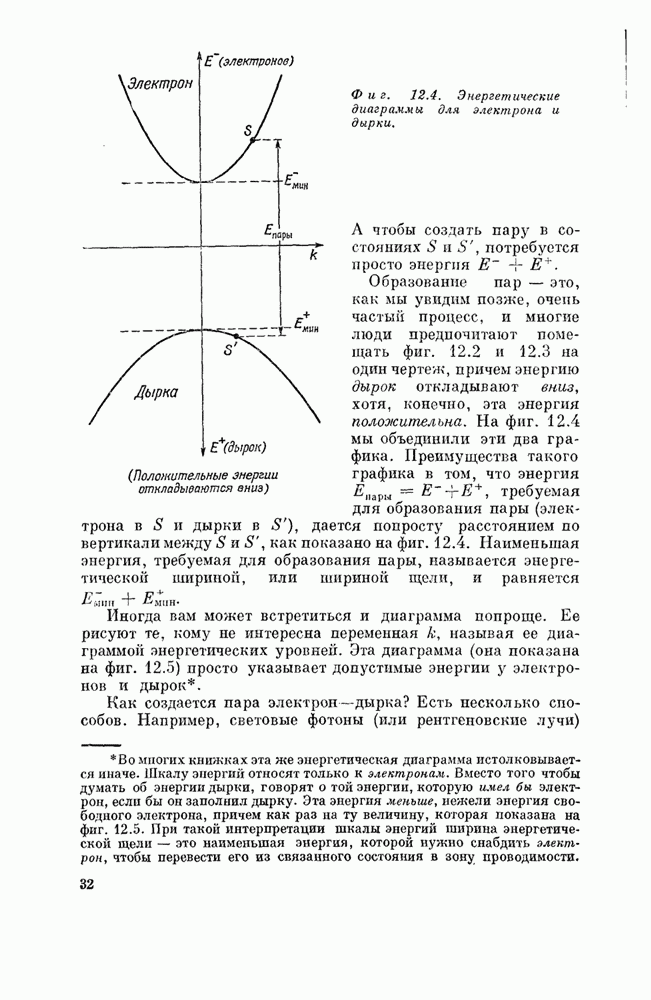
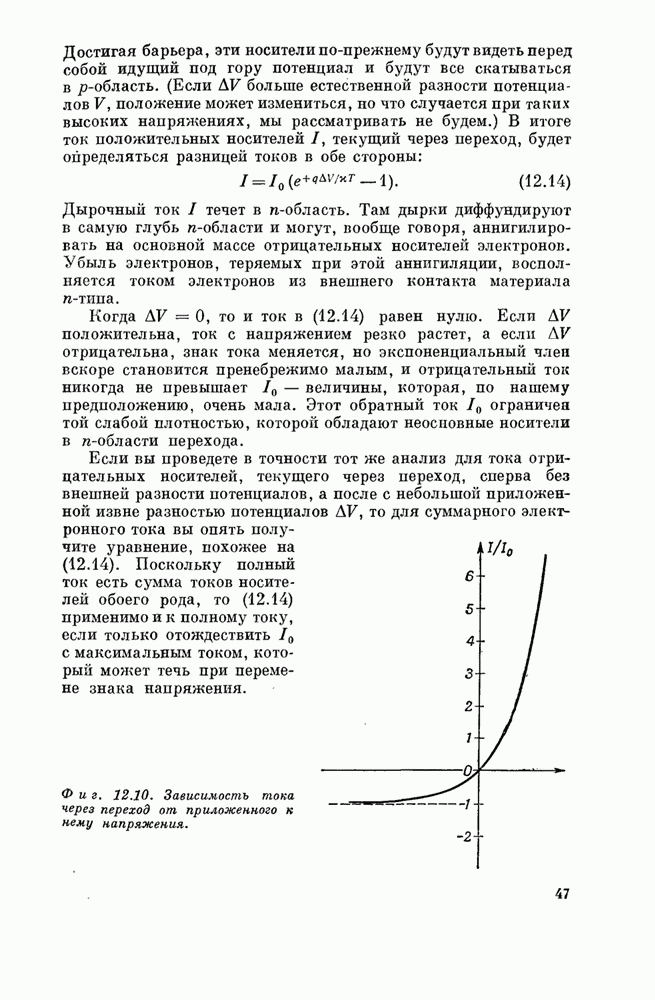
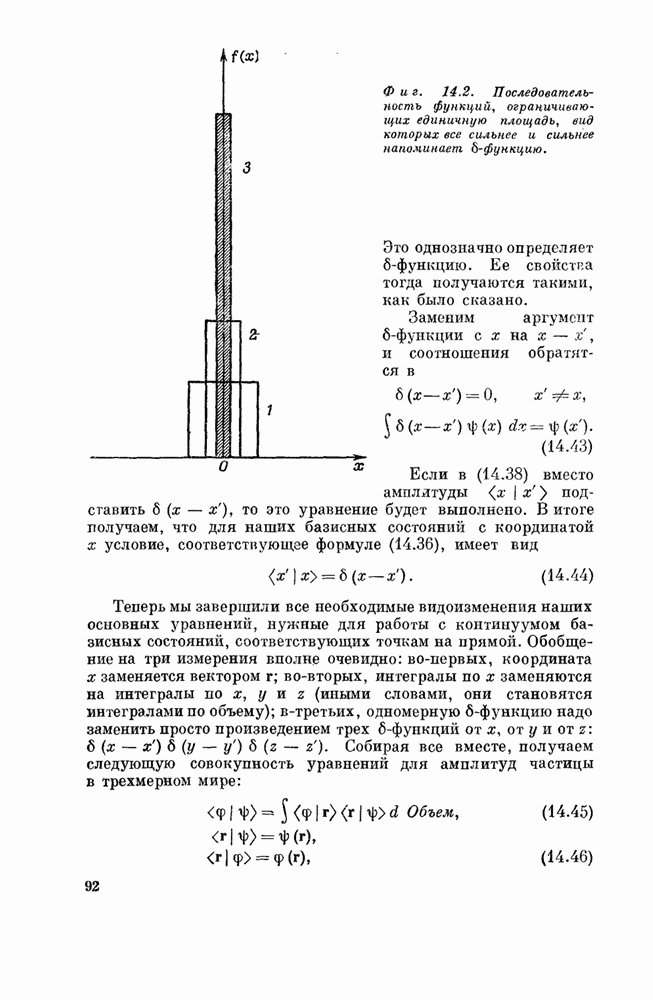
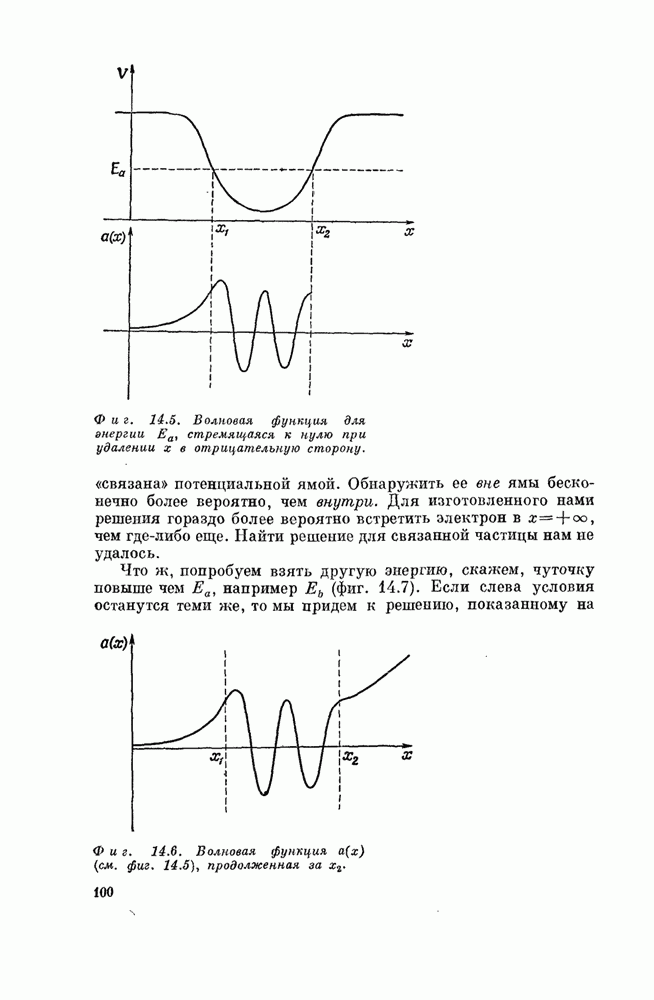
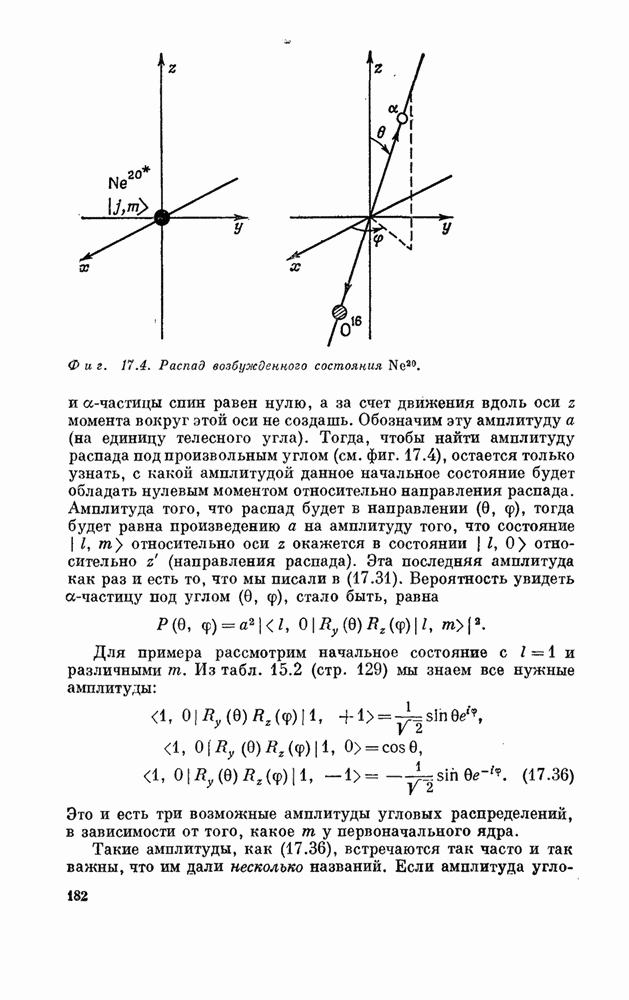
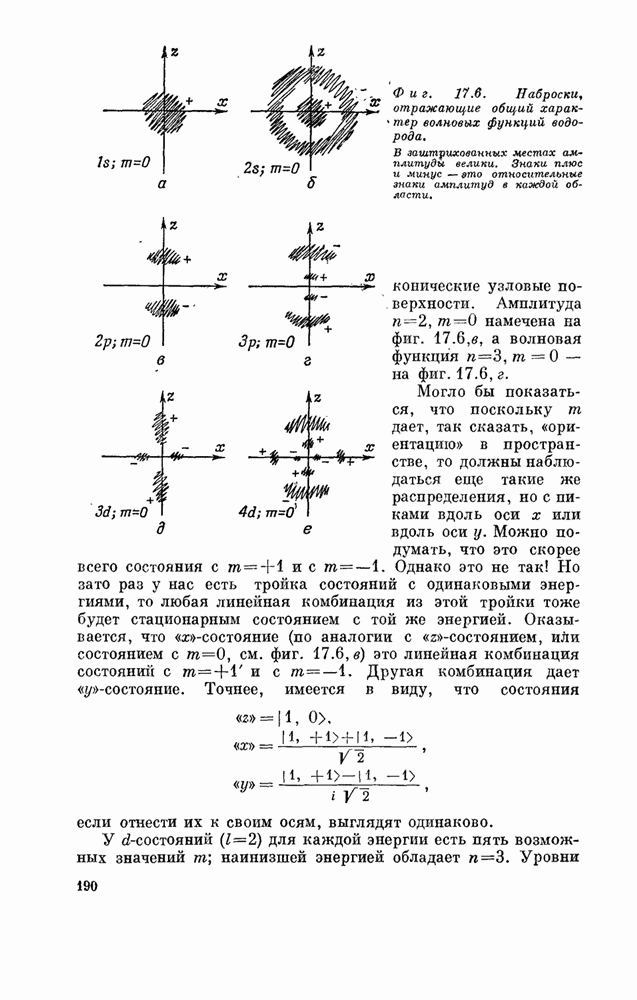
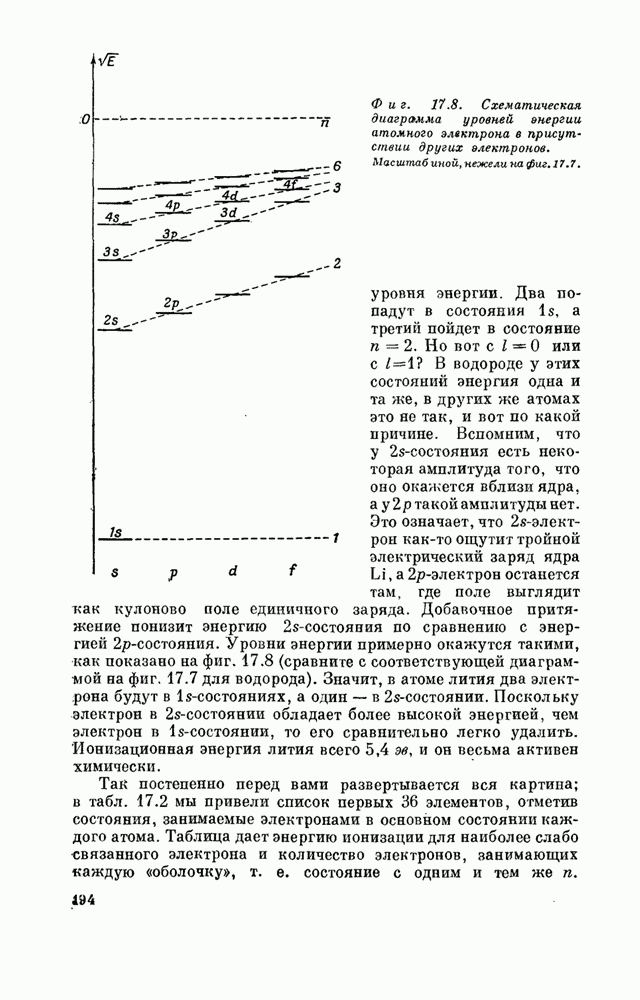
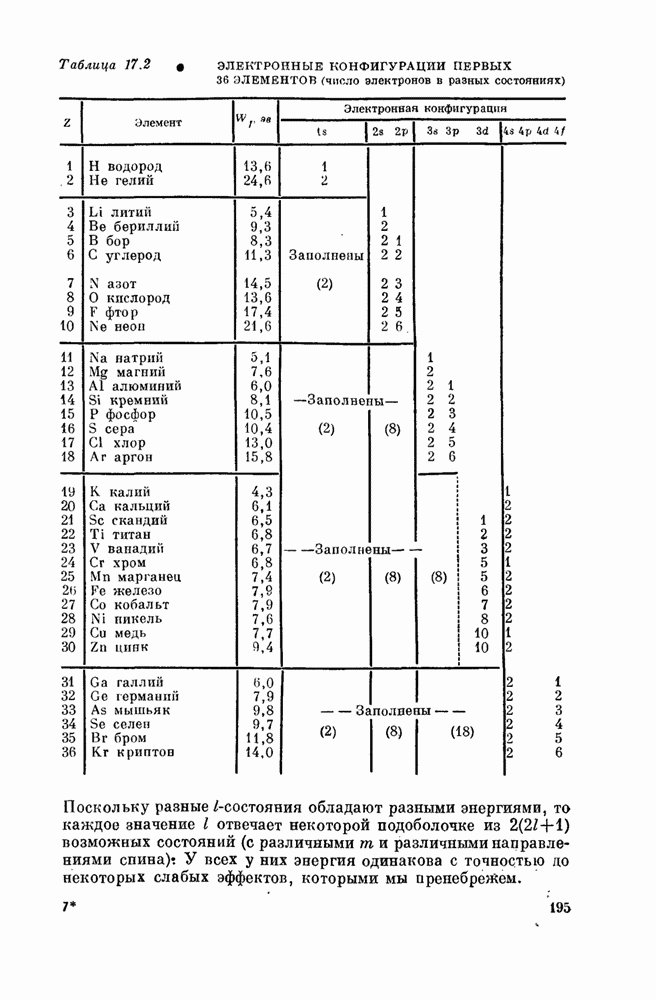
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Уравнение непрерывности для вероятностей
Перехожу
теперь ко второму пункту. Важную сторону уравнения Шредингера отдельной частицы
составляет идея о том, что вероятность обнаружить частицу в каком-то месте
определяется квадратом абсолютной величины волновой функции. Для квантовой
механики характерно также то, что вероятность сохраняется локально (т. е. в
каждом отдельном месте). Когда вероятность обнаружить электрон в таком-то месте
убывает, а вероятность обнаружить его в каком-то другом месте возрастает (так
что полная вероятность не меняется), то что-то в промежутке между этими местами
должно было произойти. Иными словами, электрон обладает непрерывностью в том
смысле, что если вероятность спадает в одном месте и возрастает в другом, то
между этими местами должно что-то протекать. Так, если вы между ними поставите
стенку, то это скажется на вероятностях и они станут не такими, как были.
Следовательно, одно только сохранение вероятности не есть полная формулировка
закона сохранения, все равно как одно только сохранение энергии не обладает
такой глубиной и не представляет такой важности, как локальное сохранение
энергии [см. гл. 27, § 1 (вып. 6)]. Если энергия исчезает, то этому должен
соответствовать отток энергии от этого места. Вот и у вероятности хотелось бы
обнаружить такой же «ток». Хотелось бы, чтобы было так: если где-нибудь
переменится плотность вероятности (вероятность обнаружить что-то там такое в
единице объема), то чтобы можно было считать, что вероятность откуда-то сюда
притекла (или утекла отсюда куда-то еще). Такой ток был бы вектором, который
можно было бы толковать следующим образом: его ![]() -компонента была бы чистой
вероятностью (в секунду и на единицу объема) того, что частица пройдет в
направлении
-компонента была бы чистой
вероятностью (в секунду и на единицу объема) того, что частица пройдет в
направлении ![]() через
плоскость, параллельную плоскости
через
плоскость, параллельную плоскости ![]() . Проход в направлении
. Проход в направлении ![]() считается
положительным потоком, а проход в обратную сторону – отрицательным потоком.
считается
положительным потоком, а проход в обратную сторону – отрицательным потоком.
Существует
ли такой ток? Вы знаете, что плотность вероятности ![]() выражается через волновую
функцию
выражается через волновую
функцию
![]() . (19.7)
. (19.7)
И
вот, я спрашиваю: существует ли такой ток ![]() , что
, что
![]() ? (19.8)
? (19.8)
Если я продифференцирую (19.7) по времени, то получу два слагаемых
![]() . (19.9)
. (19.9)
Теперь
для ![]() возьмите
уравнение Шредингера – уравнение (19.3); кроме того, комплексно его сопрягите,
т. е. перемените знак при каждом
возьмите
уравнение Шредингера – уравнение (19.3); кроме того, комплексно его сопрягите,
т. е. перемените знак при каждом ![]() , чтобы получить
, чтобы получить ![]() . У вас выйдет
. У вас выйдет
 (19.10)
(19.10)
Члены с потенциальной энергией и многие другие члены взаимно уничтожатся. А то, что останется, оказывается, действительно можно записать в виде полной дивергенции. Все уравнение целиком эквивалентно уравнению
![]() . (19.11)
. (19.11)
Не
так уж сложно, как кажется на первый взгляд. Это симметричная комбинация из ![]() , умноженного на
некоторую операцию над
, умноженного на
некоторую операцию над ![]() , плюс
, плюс ![]() , умноженное на комплексно
сопряженную операцию над
, умноженное на комплексно
сопряженную операцию над ![]() . Это просто некоторая величина плюс
комплексно сопряженная ей величина, так что все вместе (как и положено быть)
вещественно. Операция запоминается так: это попросту оператор импульса
. Это просто некоторая величина плюс
комплексно сопряженная ей величина, так что все вместе (как и положено быть)
вещественно. Операция запоминается так: это попросту оператор импульса ![]() минус
минус ![]() . Ток из (19.8) я
могу записать в виде
. Ток из (19.8) я
могу записать в виде
 . (19.12)
. (19.12)
Тогда
это и есть тот ток ![]() , который удовлетворяет уравнению
(19.8).
, который удовлетворяет уравнению
(19.8).
Уравнение
(19.8) показывает, что вероятность сохраняется локально. Если частица исчезает
из одной области, то она не может оказаться в другой без того, чтобы что-то не
протекло в промежутке между областями. Вообразите, что первая область окружена
замкнутой поверхностью, которая проведена так далеко, что имеется нулевая
вероятность обнаружить на ней электрон. Полная вероятность обнаружить электрон
где-то внутри поверхности равна объемному интегралу от ![]() . Но, согласно теореме
Гаусса, объемный интеграл от дивергенции
. Но, согласно теореме
Гаусса, объемный интеграл от дивергенции ![]() равняется поверхностному интегралу
от
равняется поверхностному интегралу
от ![]() .
Если
.
Если ![]() на
поверхности равно нулю, то (19.12) утверждает, что и
на
поверхности равно нулю, то (19.12) утверждает, что и ![]() есть нуль; значит, полная
вероятность отыскать частицу внутри поверхности не может измениться. Только
тогда, когда часть вероятности достигает границы, какая-то ее часть может
вытечь наружу. Мы вправо говорить, что она выбирается наружу только через
поверхность – это и есть локальная сохраняемость.
есть нуль; значит, полная
вероятность отыскать частицу внутри поверхности не может измениться. Только
тогда, когда часть вероятности достигает границы, какая-то ее часть может
вытечь наружу. Мы вправо говорить, что она выбирается наружу только через
поверхность – это и есть локальная сохраняемость.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 11. РАСПРОСТРАНЕНИЕ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ
- § 1. Состояния электрона в одномерной решетке
- § 2. Состояния определенной энергии
- § 3. Состояния, зависящие от времени
- § 4. Электрон в трехмерной решетке
- § 5. Другие состояния в решетке
- § 6. Рассеяние на нерегулярностях решетки
- § 7. Захват нерегулярностями решетки
- § 8. Амплитуды рассеяния и связанные состояния
- Глава 12. ПОЛУПРОВОДНИКИ
- § 1. Электроны и дырки в полупроводниках
- § 2. Примесные полупроводники
- § 3. Эффект Холла
- § 4. Переходы между полупроводниками
- § 5. Выпрямление на полупроводниковом переходе
- § 6. Транзистор
- Глава 13. ПРИБЛИЖЕНИЕ НЕЗАВИСИМЫХ ЧАСТИЦ
- § 1. Спиновые волны
- § 2. Две спиновые волны
- § 3. Независимые частицы
- § 4. Молекула бензола
- § 5. Еще немного органической химии
- § 6. Другие применения приближения
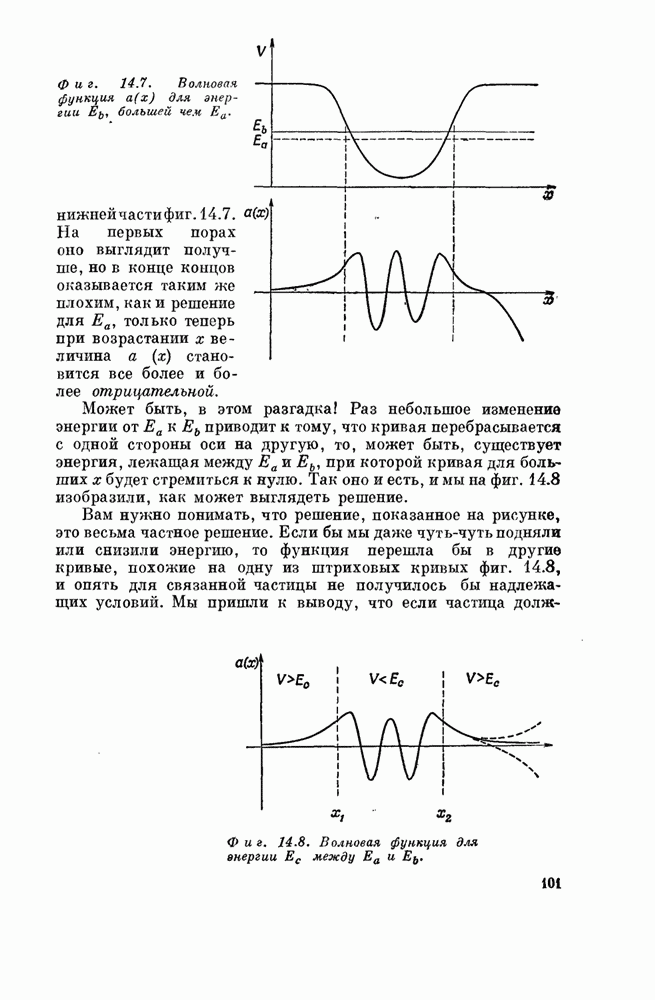
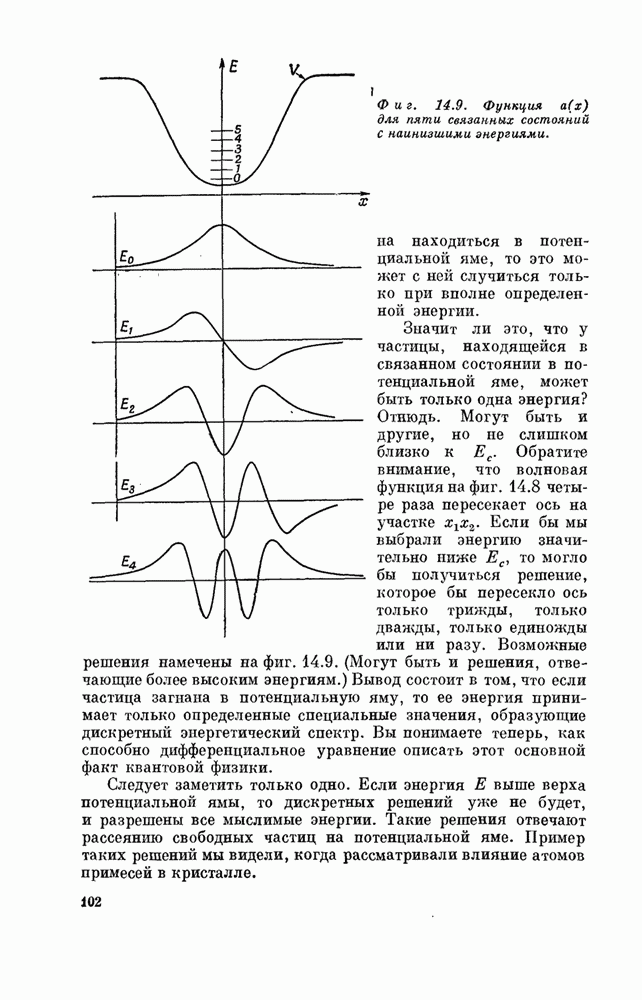
- Глава 14. ЗАВИСИМОСТЬ АМПЛИТУД ОТ МЕСТА
- § 1. Как меняются амплитуды вдоль прямой
- § 2. Волновая функция
- § 3. Состояния с определенным импульсом
- § 4. Нормировка состояний с определенной координатой x
- § 5. Уравнение Шредингера
- § 6. Квантованные уровни энергии
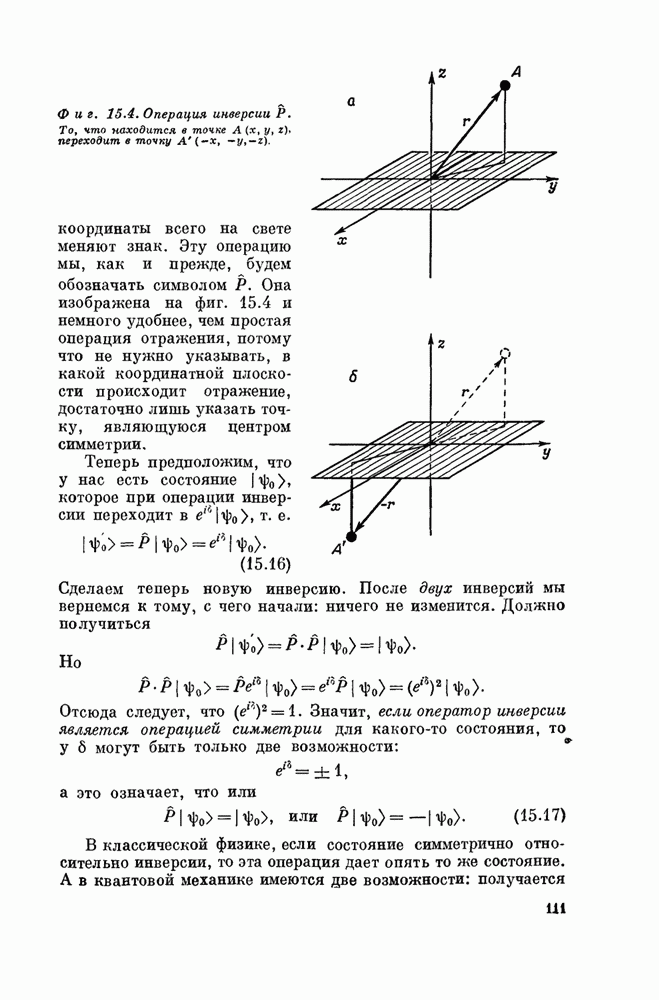
- Глава 15. СИММЕТРИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Симметрия
- § 2. Симметрия и ее сохранение
- § 3. Законы сохранения
- § 4. Поляризованный свет
- § 5. Распад
- § 6. Сводка матриц поворота
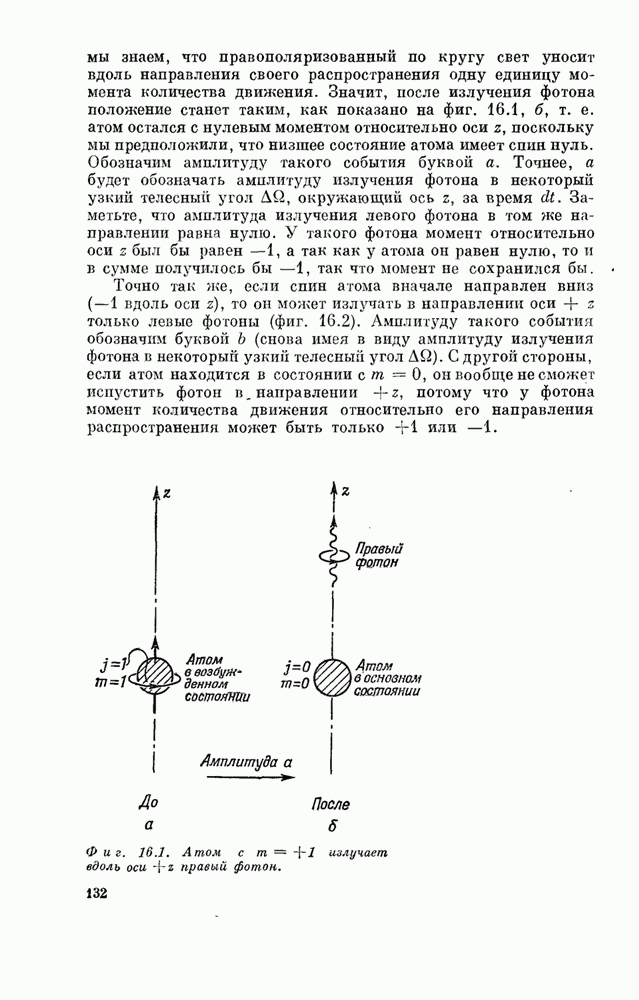
- Глава 16. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 1. Электрическое дипольное излучение
- § 2. Рассеяние света
- § 3. Аннигиляция позитрония
- § 4. Матрица поворота для произвольного спина
- § 5. Измерение ядерного спина
- § 6. Сложение моментов количества движения
- Глава 17. АТОМ ВОДОРОДА И ПЕРИОДИЧЕСКАЯ ТАБЛИЦА
- § 1. Уравнение Шредингера для атома водорода
- § 2. Сферически симметричные решения
- § 3. Состояния с угловой зависимостью
- § 4. Общее решение для водорода
- § 5. Волновые функции водорода
- § 6. Периодическая таблица
- Глава 18. ОПЕРАТОРЫ
- § 1. Операции и операторы
- § 2. Средние энергии
- § 3. Средняя энергия атома
- § 4. Оператор места
- § 5. Оператор импульса
- § 6. Момент количества движения
- § 7. Изменение средних со временем
- Глава 19. УРАВНЕНИЕ ШРЕДИНГЕРА В КЛАССИЧЕСКОМ КОНТЕКСТЕ. СЕМИНАР ПО СВЕРХПРОВОДИМОСТИ
- § 1. Уравнение Шредингера в магнитном поле
- § 2. Уравнение непрерывности для вероятностей
- § 3. Два рода импульсов
- § 4. Смысл волновой функции
- § 5. Сверхпроводимость
- § 6. Явление Мейсснера
- § 7. Квантование потока
- § 8. Динамика сверхпроводимости
- § 9. Переходы Джозефсона
- Эпилог
- От редактора перевода